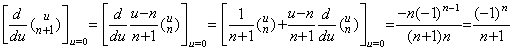3. 微分演算子の導入
3.1 微分演算子の概略
. .
関数 y(t) が連続微分可能なら、ベクトル Y 及び Y' は関数及びその一次導関数の階差により得られる。両ベクトルの関係は行列演算式 Y' =AY で表される。微分演算は関数ではないから行列 A はベクトルの行列展開ではない。ベクトルの形式を持たない商か、又は、商ではない演算子である。従って、行列 A を2つのベクトル Y と Y' だけから計算で得ることは出来ない。あらゆる連続微分可能関数とその一次導関数のベクトルを用いて計算しなければならない。
. .
関数が定数、即ち、y(t)=c0 であるなら導関数は y' (t)=0 である。従って、行列演算式は 0=Ac01 である。これは、行列 A の第1列の全要素は零であることを必要とする。関数が y(t)=c0+c1t なら導関数は y' (t)=c1 である。従って、行列演算式は c11=A(c0, c1h, 0, ……) である。これは、第2列は第1要素が 1/h である以外は、他の要素は全て零であることを必要とする。関数が y(t)=c0+c1t+c2t2 であるなら導関数は y' (t)=c1+2c2t であり、従って、
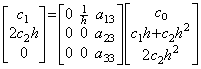 ___∴_ ___∴_
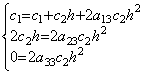 ___∴_ ___∴_
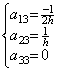 関数が y(t)=c0+c1t+c2t2+c3t3 なら導関数は y' (t)=c1+2c2t+3c3t2 であり、従って、
関数が y(t)=c0+c1t+c2t2+c3t3 なら導関数は y' (t)=c1+2c2t+3c3t2 であり、従って、
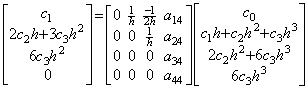 ___∴_ ___∴_
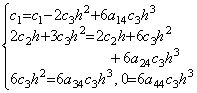
∴_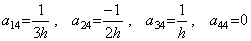 . .
更にこの繰返しを行うと、著者が (1/h)ΔD と表す微分演算子が得られる。この三角行列 ΔD は下に示す第1行を持ち、他の行の要素はその上の行と同じであるが、1要素右にシフトされたものである。 . .
更にこの繰返しを行うと、著者が (1/h)ΔD と表す微分演算子が得られる。この三角行列 ΔD は下に示す第1行を持ち、他の行の要素はその上の行と同じであるが、1要素右にシフトされたものである。
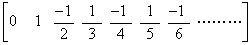
. .
しかし、この行列が全ての連続微分可能関数について成立することをこの方法で証明するのは困難である。その証明は、関数が p+1 階連続微分可能関数なら Newton の剰余項付き補間公式及びその導関数を用いて行われる。従って、本演算子法ではこの後はそのような関数の微分を扱う。
3.2 ニュートンの剰余項付き補間公式
. .
通常は、Newton の補間公式の剰余項は等間隔区分点では分母が零になるという理由で意味を持たない項を用いて求められる。これはその公式の微分に障害を生ずる。それ故、著者は Newton の剰余項付き補間公式をその問題のある項を使用せずに、範囲 [a, b] を区分幅 h で p+1 等間隔区分点に区分して求める。
. .[定理 3.1]__y(t)∈Cp+1[a, b] のとき、任意の実数 q に対して t=t0+qh∈[a, b] とすれば、
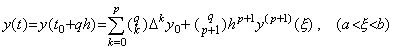 _____(3.1)
[証明]__t=t0+qh における剰余項を次のように仮定する。 _____(3.1)
[証明]__t=t0+qh における剰余項を次のように仮定する。
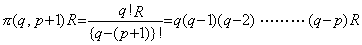 _____(3.2)
これは q=0, 1, 2, ……, p において剰余項は零でなければならないという条件を満たしている。故に、 _____(3.2)
これは q=0, 1, 2, ……, p において剰余項は零でなければならないという条件を満たしている。故に、
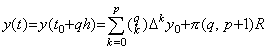 _____(3.3). .
R は q の関数である。関数 R が、ある非整数の q に対する値 Rq の定数である近似公式を考えると、t=t0+uh において y(t) とこの近似公式の差を表す関数 F(u) は次のようになる。 _____(3.3). .
R は q の関数である。関数 R が、ある非整数の q に対する値 Rq の定数である近似公式を考えると、t=t0+uh において y(t) とこの近似公式の差を表す関数 F(u) は次のようになる。
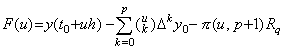 _____(3.4). .
関数 F(u) は u=0, 1, 2, ……, p 及び q の p+2 点で零になる。従って、Rolle の定理により、これら u の最小値と最大値の間の或る点で F(p+1)(u)=0 が成立する。その点を ξ=t0+uh で表すと、 _____(3.4). .
関数 F(u) は u=0, 1, 2, ……, p 及び q の p+2 点で零になる。従って、Rolle の定理により、これら u の最小値と最大値の間の或る点で F(p+1)(u)=0 が成立する。その点を ξ=t0+uh で表すと、
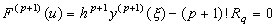
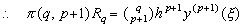 _____(3.5) _____(3.5)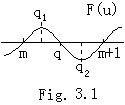 . .
(3.5)は q が整数でも成立することは次のようにして示すことが出来る。或る整数 m に対して m<q<m+1 と仮定すると、関数 F(u) はこの近辺で概略 Fig. 3.1 で図示できる。関数 R は(3.3)により連続であるから、q→m に対する極限 R→Rm 及び ξ→ξm が存在して、 . .
(3.5)は q が整数でも成立することは次のようにして示すことが出来る。或る整数 m に対して m<q<m+1 と仮定すると、関数 F(u) はこの近辺で概略 Fig. 3.1 で図示できる。関数 R は(3.3)により連続であるから、q→m に対する極限 R→Rm 及び ξ→ξm が存在して、
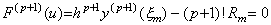 _____(3.6) _____(3.6)
である。従って、(3.5)は等間隔区分点 m においても成立する。__________[証明終]
__
[定理 3.2]____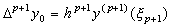 _______(3.7) _______(3.7)
[証明]__(3.1)に q=p+1 を代入すると、Fig. 3.1 において関数 F(u) は横軸と m+1 では交差しないけれども、m=p 及び q→m+1 を実行することが出来るから、(3.6)を満たす ξp+1 が存在する。従って、
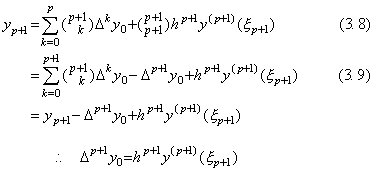 [証明終] [証明終]
. .
範囲 [a, b] が区間幅 h の p+1 個の区間からなるとき、関数 y(t) は範囲 [a, b−h] において(3.1)で表され、剰余項は y0, y1, ……, yp においては零である。しかし、その延長上の yp+1 の剰余項は(3.8)に示すように通常は零ではなく、Δp+1y0 で与えられる値を持つ。故に、関数値 yp+1 は(3.9)に示すように p+1 次関数上にある。y(p+1)(t)≡0 なら関数 y(t) は p 次関数である。|y(p+1)(t)|≤M を満たすような M が存在するなら、h→0 に対して Δp+1y0→0 が成立し、関数値 yp+1 は h が小さいとき十分な近似精度で p 次関数上にある。従って、関数 y(t) は範囲 [a, b] において剰余項を持たない(3.1)及び次のベクトルで表すことが出来る。
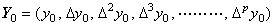 _____(3.10). .
yp+1 に対して Δp+1y0 が無視できないときはその関数は p+1 次以上の補間公式により近似されなければならない。しかし、関数 y(p+1)(t) がもう微分可能でないなら、範囲 [a, b] をもっと小さい範囲に分割して p 次の補間公式で関数 y(t) を近似しなければならない。 _____(3.10). .
yp+1 に対して Δp+1y0 が無視できないときはその関数は p+1 次以上の補間公式により近似されなければならない。しかし、関数 y(p+1)(t) がもう微分可能でないなら、範囲 [a, b] をもっと小さい範囲に分割して p 次の補間公式で関数 y(t) を近似しなければならない。
. .
一般的には、(3.1)の剰余項の正確な値を求めることは難しい。上記の Δp+1y0 の性質により近似的に Δp+1y0 を剰余項の hp+1y(p+1)(ξ) に代入すると、結果は剰余項のない p+1 次の補間公式となる。故に、Δp+1y0 が零でないならこれを範囲 [a, b] における補間公式の概略の精度と考えることが出来る。従って、微分方程式を可変次数及び可変区分幅解法で解く際に、これを次数及び区分幅が適当であるか否か、及び、解が収束しているか否かを判断するために使用することが出来る。
. .
関数 y(p)(t) が微分可能でないなら剰余項は得られない。その場合でも、Δp+1y0 を(3.9)の hp+1y(p+1)(ξ) に代入すれば関数値 yp+1 は剰余項のない p+1 次の補間公式で正しく表される。従って、最上階の階差 Δp+1y0 は p 次の補間公式による範囲 [a, b] における関数の近似精度を与えると考えてよい。しかし、定理 3.2 はその場合には成立しないから Δp+1y0→0 が保証されるか否かは定かでない。
. .
例えば、(3.11)は第1章第 3.4 節で述べた微分方程式 y' = √y, y0=0 の解の1つである。
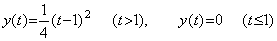 _____(3.11)
これは2次導関数が t=1 で連続でないから C1[0, 2] の関数である。2次導関数は t≤1 では y"(t)=0 であり、t>1 では y"(t)=1/2 になる。範囲を h=1 で2つの等間隔区間に区分すると、この関数は範囲 [0, 1] では p=1 で剰余項は零の(3.1)で表される。その延長上の値 y2 は剰余項の R の値が Δ2y0=1/4 であることを必要とし、関数 y(t) は範囲 [0, 2] において(3.12)で近似できる。定理 3.1 及び 3.2 はこの場合は成立せず、R の値は2つの h2y"(t) の平均値に等しい。 _____(3.11)
これは2次導関数が t=1 で連続でないから C1[0, 2] の関数である。2次導関数は t≤1 では y"(t)=0 であり、t>1 では y"(t)=1/2 になる。範囲を h=1 で2つの等間隔区間に区分すると、この関数は範囲 [0, 1] では p=1 で剰余項は零の(3.1)で表される。その延長上の値 y2 は剰余項の R の値が Δ2y0=1/4 であることを必要とし、関数 y(t) は範囲 [0, 2] において(3.12)で近似できる。定理 3.1 及び 3.2 はこの場合は成立せず、R の値は2つの h2y"(t) の平均値に等しい。
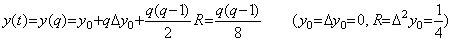 _____(3.12). .
範囲を区分幅 h=2/3 で3つの等区間に区分すると、関数は範囲 [0, 4/3] において p=2, y0=Δy0=0 及び Δ2y0=1/36 の(3.1)で表される。但し、y(3)(t)≡0 にもかかわらず剰余項は零ではない。この延長上の関数値 y3 は剰余項の R の値が Δ3y0=1/6 であることを必要とする。この場合、関数 y(t) は範囲 [0, 2] 全体では(3.13)に示すように3次の補間公式で近似できる。 _____(3.12). .
範囲を区分幅 h=2/3 で3つの等区間に区分すると、関数は範囲 [0, 4/3] において p=2, y0=Δy0=0 及び Δ2y0=1/36 の(3.1)で表される。但し、y(3)(t)≡0 にもかかわらず剰余項は零ではない。この延長上の関数値 y3 は剰余項の R の値が Δ3y0=1/6 であることを必要とする。この場合、関数 y(t) は範囲 [0, 2] 全体では(3.13)に示すように3次の補間公式で近似できる。
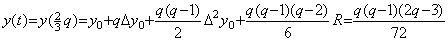 _____(3.13). .
範囲を h=1/2 で4つの等区間に区分すると、関数は範囲 [0, 3/2] において p=3, y0=Δy0=Δ2y0=0 及び Δ3y0=1/16 の(3.1)で表される。但し、剰余項は y(4)(t)≡0 及び Δ4y0=0 にもかかわらず零ではない。剰余項の R に Δ4y0=0 を代入すると、(3.14)に示すように関数 y(t) は範囲 [0, 2] 全体ではやはり3次の補間公式で近似される。しかし、(3.13)及び(3.11)のどちらとも等しくない。 _____(3.13). .
範囲を h=1/2 で4つの等区間に区分すると、関数は範囲 [0, 3/2] において p=3, y0=Δy0=Δ2y0=0 及び Δ3y0=1/16 の(3.1)で表される。但し、剰余項は y(4)(t)≡0 及び Δ4y0=0 にもかかわらず零ではない。剰余項の R に Δ4y0=0 を代入すると、(3.14)に示すように関数 y(t) は範囲 [0, 2] 全体ではやはり3次の補間公式で近似される。しかし、(3.13)及び(3.11)のどちらとも等しくない。
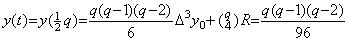 _____(3.14). .
与えられた関数の連続微分可能階数より高次の補間公式では、上記に述べたように、最高階差は公式の精度の正しい評価を与えない。従って、範囲を小さい範囲に分割してそれより低次の補間公式を使用しなければならない。上記の例では、範囲を [0, 1] 及び [1, 2] に分割したとき最良の結果を得る。故に、上記の微分方程式は第1章第 3.4 節で述べたように解が恒等的に零である場合と恒等的には零でない場合について解かねばならない。 _____(3.14). .
与えられた関数の連続微分可能階数より高次の補間公式では、上記に述べたように、最高階差は公式の精度の正しい評価を与えない。従って、範囲を小さい範囲に分割してそれより低次の補間公式を使用しなければならない。上記の例では、範囲を [0, 1] 及び [1, 2] に分割したとき最良の結果を得る。故に、上記の微分方程式は第1章第 3.4 節で述べたように解が恒等的に零である場合と恒等的には零でない場合について解かねばならない。
3.3 ニュートンの補間公式の差分
. .
関数 y(t)∈Cp+1[a, b] のこれをシフトした関数 y(t+h) からの減算を Δy(t)=y(t+h)−y(t) で表すと、関数 Δy(t) は等間隔区分幅 h の区分点 t0, t1, t2, ……… に対する階差 Δy0, Δy1, Δy2, ……… を与えるものであり、ベクトルの階差で表される。
. .[定理 3.3]. .
関数が y(t)∈Cp+1[a, b] のとき、t=t0+rh∈[a, b] となる任意の実数 r に対して、
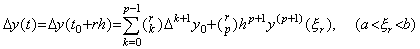 _____(3.15)
[証明]. .関数 y(t+h) は y(t) を t 軸に平行に −h シフトすることにより得られるものであるから、(3.3)をシフトすることにより次の補間公式により表され、剰余項は q=−1, 0, 1, 2, ………, p−1 の p+1 点で零になる。 _____(3.15)
[証明]. .関数 y(t+h) は y(t) を t 軸に平行に −h シフトすることにより得られるものであるから、(3.3)をシフトすることにより次の補間公式により表され、剰余項は q=−1, 0, 1, 2, ………, p−1 の p+1 点で零になる。
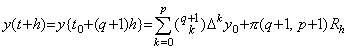 _____(3.16) _____(3.16)
| __ |  |
. .q−1 に対する関数値 y(t+h) は q に対する関数値 y(t) に等しいから、q−1 に対する Rh の値は(3.3)の q に対する R の値に等しい。従って、関数 Rh の値を(3.4)で固定された定数 Rq に固定するなら、この近似関数の(3.16)の関数からの差は t=t0+uh に対して(3.17)で表され、関数 G(u) は G(u)=F(u+1) であるから u=−1, 0, 1, 2, ………, p−1 及び q−1 の p+2 点で零になる。
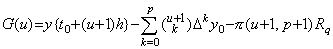 _____(3.17) _____(3.17)
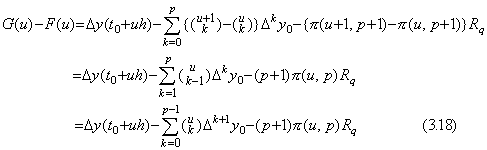
| __ |  |
. .
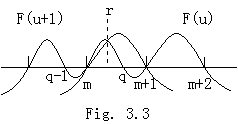
関数 G(u)−F(u) は u=0, 1, 2, ………, p−1 及び Fig. 3.3 に示すように q−1<r<q となるような r の p+1 点で零になる。故に、p 次の導関数はこれら u の値の最小値と最大値の間のある値で Rolle の定理により零になる。その点を ξ=t0+uh とすると、
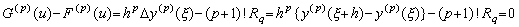 となり、関数 y(p)(t) はもう一度微分可能であるから、ξ<ξ r<ξ+h を満たすような或る値 ξ r が存在して、
となり、関数 y(p)(t) はもう一度微分可能であるから、ξ<ξ r<ξ+h を満たすような或る値 ξ r が存在して、
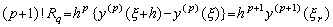 であり、(3.18)において G(r)−F(r)=0 が満たされる。従って、(3.15)は任意の非整数 r に対して成立する。これは又整数 r についても成立する。何故なら、Fig. 3.3 に示すように、m<r<q の場合は q→m の実行により、又、q−1<r<m の場合は q→m+1 の実行により r→m が得られるからである。
であり、(3.18)において G(r)−F(r)=0 が満たされる。従って、(3.15)は任意の非整数 r に対して成立する。これは又整数 r についても成立する。何故なら、Fig. 3.3 に示すように、m<r<q の場合は q→m の実行により、又、q−1<r<m の場合は q→m+1 の実行により r→m が得られるからである。
______________________________________[証明終]
. .
(3.15)の剰余項は r<p なる整数 r に対しては零である。r=p の場合は、常には零ではなく、Δyp は次のように表される。従って、p+1 階の階差は剰余項に等しい。
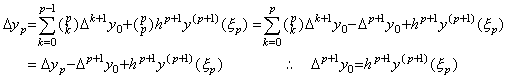 . .
関数 y(t) がベクトル Y0 で表されるとき、hp+1y(p+1)(t)→0 であるから p+1 階の階差は Δp+1y0→0 になる。故に、関数 Δy(t) は範囲 [a, b] において剰余項のない(3.15)に同じ p−1 次の公式で表せる。従って、次のベクトルで表すことが出来る。 . .
関数 y(t) がベクトル Y0 で表されるとき、hp+1y(p+1)(t)→0 であるから p+1 階の階差は Δp+1y0→0 になる。故に、関数 Δy(t) は範囲 [a, b] において剰余項のない(3.15)に同じ p−1 次の公式で表せる。従って、次のベクトルで表すことが出来る。
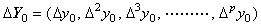 _____(3.19). .
ΔY0 をスカラー Δ とベクトル Y0=(y0, Δy0, Δ2y0, ……, Δpy0) の積と考えると、結果の最後の要素は Δp+1y0 である。それは階差 ΔY0=Y1−Y0 の最後の要素に等価である。しかし、Δp+1y0→0 であるからベクトル ΔY0 の表記では省略してよい。従って、ベクトル Y1 及び Y0 の最後の要素は等価、即ち、Δpy1=Δpy0 である。実際に、ΔY0 の記号 Δ は行列で表される演算子であり、上記の関係は次のように表される。 _____(3.19). .
ΔY0 をスカラー Δ とベクトル Y0=(y0, Δy0, Δ2y0, ……, Δpy0) の積と考えると、結果の最後の要素は Δp+1y0 である。それは階差 ΔY0=Y1−Y0 の最後の要素に等価である。しかし、Δp+1y0→0 であるからベクトル ΔY0 の表記では省略してよい。従って、ベクトル Y1 及び Y0 の最後の要素は等価、即ち、Δpy1=Δpy0 である。実際に、ΔY0 の記号 Δ は行列で表される演算子であり、上記の関係は次のように表される。
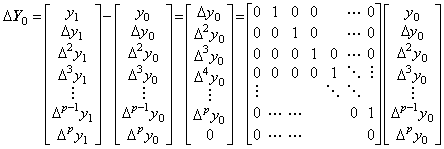 ___(3.20) ___(3.20)
3.4 ニュートンの補間公式の微分
. .
y(t)∈Cp+1[a, b] のとき y' (t)∈Cp[a, b] であるから、導関数は Δp−1y0' 迄の階差を用いた Newton の剰余項付き補間公式で表されねばならない。従って、その公式は y(t) の公式より一次低次となる。y(t) と y' (t) の関係を求めるために、等間隔区分幅 h は同じものでなければならないから範囲 [a, b] は p+1 の等区間に分割しなければならない。
. .[定理 3.4]. .y' (t)∈Cp[a, b] のとき、t=t0+qh∈[a, b] なる任意の実数 q に対して、
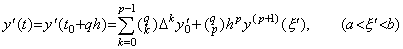 ____(3.21)
[証明]. .定理 3.1 の証明における y(t) に y' (t) を、p に p−1 を代入すると、(3.3) 及び (3.4)は次式になる。 ____(3.21)
[証明]. .定理 3.1 の証明における y(t) に y' (t) を、p に p−1 を代入すると、(3.3) 及び (3.4)は次式になる。
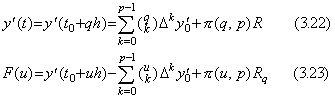 . .
q の値が整数でないなら、関数 F(u) は u=0, 1, 2, ………, p−1 及び q の p+1 点で零になる。従って、Rolle の定理により p 次の導関数はこれら u の値の最小値と最大値の間の或る点で零になる。その u の値を ξ' =t0+uh とすれば、 . .
q の値が整数でないなら、関数 F(u) は u=0, 1, 2, ………, p−1 及び q の p+1 点で零になる。従って、Rolle の定理により p 次の導関数はこれら u の値の最小値と最大値の間の或る点で零になる。その u の値を ξ' =t0+uh とすれば、
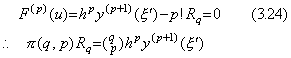 . .
q の値が整数なら、定理 3.1 の証明で述べたように(3.24)に対して q→m を実行することにより証明される。_____________________[証明終] . .
q の値が整数なら、定理 3.1 の証明で述べたように(3.24)に対して q→m を実行することにより証明される。_____________________[証明終]
. .
(3.21)に q=p を代入すると、定理 3.2 の証明と同様の方法により、Δpy0' は剰余項になる。それは(3.21)の剰余項において hpy(p+1)(ξ' ) の代わりに近似的に用いることが出来る。
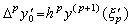 _____(3.25). .
ベクトル Y0 が Δpy0 迄の要素により定義されるとき、h→0 に対して hpy(p+1)(t)→0 が成立する。従って、関数 y' (t) は範囲 [a, b] において p−1 次の公式、即ち、剰余項のない(3.21)により十分な精度で近似される。故に、次のベクトルで表される。 _____(3.25). .
ベクトル Y0 が Δpy0 迄の要素により定義されるとき、h→0 に対して hpy(p+1)(t)→0 が成立する。従って、関数 y' (t) は範囲 [a, b] において p−1 次の公式、即ち、剰余項のない(3.21)により十分な精度で近似される。故に、次のベクトルで表される。
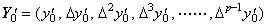 _____(3.26). .
Y0' と Y0 の関係は(3.1)の Newton の補間公式を微分することにより導かねばならない。しかし、剰余項の導関数 y(p+1)(t) はもはや t に関して連続微分可能でないし、関数 ξ は q 又は t の関数として明確に表すことが出来ないから、その微分は関数 F(u) を用いて間接的に実行しなければならない。 _____(3.26). .
Y0' と Y0 の関係は(3.1)の Newton の補間公式を微分することにより導かねばならない。しかし、剰余項の導関数 y(p+1)(t) はもはや t に関して連続微分可能でないし、関数 ξ は q 又は t の関数として明確に表すことが出来ないから、その微分は関数 F(u) を用いて間接的に実行しなければならない。
. .[定理 3.5]. . y(t)∈Cp+1[a, b] のとき、t=t0+mh∈[a, b] なる任意の整数 m に対して、
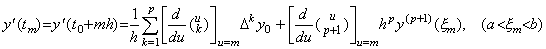 _____(3.27)
[証明]. .公式(3.3)の剰余項の R が m<q<m+1 なるある実数 q に対する値である Rq の定数であるとき、この近似関数と関数 y(t) の差 F(u) は(3.4)で表される。これを u で微分すると、k=0 の項は消えて次のようになる。 _____(3.27)
[証明]. .公式(3.3)の剰余項の R が m<q<m+1 なるある実数 q に対する値である Rq の定数であるとき、この近似関数と関数 y(t) の差 F(u) は(3.4)で表される。これを u で微分すると、k=0 の項は消えて次のようになる。
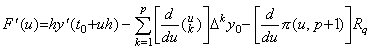 _____(3.28). .
定理 3.1 の証明の Fig. 3.1 に示したように、m<q1<q かつ F' (q1)=0 となるような点 q1 が存在する。この点 q1 は q→m に対して q1→m となり、導関数 F' (u) は u に関して連続であり、剰余項の R は q に関して連続関数であるから、ξ→ξm となる或る値 ξm が存在する。故に、 _____(3.28). .
定理 3.1 の証明の Fig. 3.1 に示したように、m<q1<q かつ F' (q1)=0 となるような点 q1 が存在する。この点 q1 は q→m に対して q1→m となり、導関数 F' (u) は u に関して連続であり、剰余項の R は q に関して連続関数であるから、ξ→ξm となる或る値 ξm が存在する。故に、
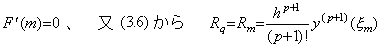 _____[証明終] _____[証明終]
. .
上記の証明から整数でない r に対する導関数 y' (t0+rh) が次のように表されることは明らかである。
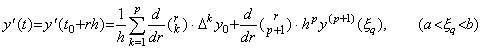 ___(3.29)
ここで、ξ の値は関数値 y(t0+rh) の剰余項を与える ξ r ではなく、m<r<q<m+1 且つ F' (r)=0 を満たす q の値に対する関数値 y(t0+qh) の剰余項を与える ξ q であることに注意が必要である。 ___(3.29)
ここで、ξ の値は関数値 y(t0+rh) の剰余項を与える ξ r ではなく、m<r<q<m+1 且つ F' (r)=0 を満たす q の値に対する関数値 y(t0+qh) の剰余項を与える ξ q であることに注意が必要である。
. .
微分係数 dπ(u, p+1)/du は π(u, p+1) から各因数を1つ除いて得られる全ての項の総和であるので、u の値が p+1 より小さい整数であってもそれらの項の1つは常に存在するから零にならない。従って、(3.27)の剰余項は 、y(p+1)(ξm) が零でないなら等間隔区分点で零にならない。h のべき指数も y(t) の補間公式のそれより小さい。故に、数値微分は関数の数値近似よりも一般的には精度が低い。
. .[定理 3.6]
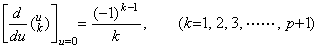 ______(3.30)
[証明]. .1). .k=1 なら_____ ______(3.30)
[証明]. .1). .k=1 なら_____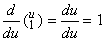
2). .k=2 なら. .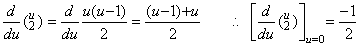
3). .k=n で成立すれば、k=n+1 では、
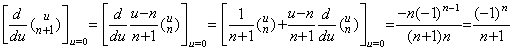 |
| [証明終] |
. .
定理 3.5 及び 3.6 により、Newton の剰余項付き補間公式の微分公式は t=t0 において次のように表される。
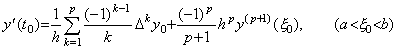 _____(3.31) _____(3.31)
. .
[定理 3.7]. .整数 m≥1 及び k≥2 に対して、
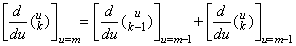 但し、k=1 のとき、. . 但し、k=1 のとき、. .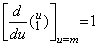 ____(3.32)
[証明]. .k=1 に対しては定理 3.6 の証明の第1項により明らかに成立する。 ____(3.32)
[証明]. .k=1 に対しては定理 3.6 の証明の第1項により明らかに成立する。
k≥2 に対しては u−1=v を代入すると、
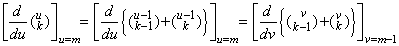 _____[証明終] _____[証明終]
. .
k≥2 の場合、y' m の第 k 項の係数は定理 3.7 により y' m−1 の第 k−1 項と第 k 項の係数の和である。従って、Newton の剰余項付き補間公式の t=t0+mh に対する微分公式は(3.31)から m の増加順に次のように得られる。
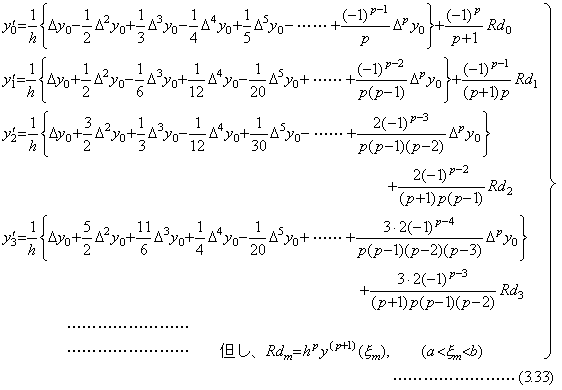 . .
上記公式の係数は次の2つの定理に示されるように一般形で表される。 . .
上記公式の係数は次の2つの定理に示されるように一般形で表される。
. .[定理 3.8]. .k≥m+1 に対して、
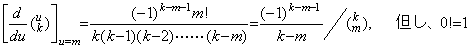 ____(3.34)
[証明]. .m=0 のときは定理 3.6 と同じである。m≥1 のときは定理 3.6 及び 3.7 により、 ____(3.34)
[証明]. .m=0 のときは定理 3.6 と同じである。m≥1 のときは定理 3.6 及び 3.7 により、
1). .m=1 のとき、k≥2に対し、
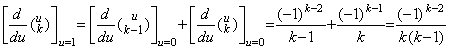 2). .m=n 且つ k≥n+1 のとき成立すれば、m=n+1 且つ k≥n+2 のときは、
2). .m=n 且つ k≥n+1 のとき成立すれば、m=n+1 且つ k≥n+2 のときは、
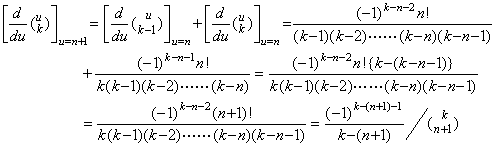 [証明終] [証明終]
. .
k≤m のときは分母が零になるので、一般形は定理 3.8 の形式で表すことが出来ない。従って、定理 3.9 の級数の k−1<m の場合で表される。
. .[定理 3.9]
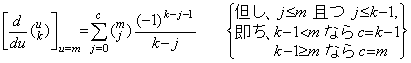 _____(3.35)
[証明] _____(3.35)
[証明]
| 1) | . .m=0 なら k≥1 に対して c=0 であり、j=0 且つ 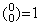 であるから(3.35)は定理 3.6 になる。 であるから(3.35)は定理 3.6 になる。 |
| 2) | . .m=1 なら k=1 に対して c=0 又は k≥2 に対して c=1 である。k=1 なら(3.35)の両辺は 1 になる。
k=2 なら、
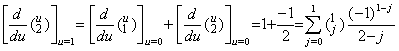 (3.35)が k=n のとき成立すれば、次に示すように k=n+1 のときも成立する。
(3.35)が k=n のとき成立すれば、次に示すように k=n+1 のときも成立する。
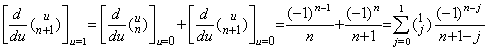 故に、m=1 に対して成立する。
故に、m=1 に対して成立する。 |
| 3) | . . m=p に対して成立するなら以下のように m=p+1 に対して成立する。
k=1 なら全ての m に対して c=0 であるから両辺は 1 になる。
k=2 なら m=p+1≥2 であるから c=k−1=1 である。故に、
 k=n のとき成立するなら、k=n+1 のとき以下のように成立する。c は k−1 又は m の小さい方に等しいから、c に関する条件は n と p の関係により Table 3.1 のように決定される。
k=n のとき成立するなら、k=n+1 のとき以下のように成立する。c は k−1 又は m の小さい方に等しいから、c に関する条件は n と p の関係により Table 3.1 のように決定される。
| Table 3.1 |
| | m=p 且つ k=n | m=p 且つ k=n+1 | m=p+1 且つ k=n+1 | |
| n<p | | k−1<m__∴ c=n−1 | k−1<m__∴ c=n | k−1<m__∴ c=n |
| n=p | | k−1<m__∴ c=n−1 | k−1=m__∴ c=p=n |
| n>p | | k−1≥m__∴ c=p | k−1>m__∴ c=p | k−1≥m__∴ c=p+1 |
. .
従って、n≤p 及び n>p の2つの場合があることになる。n≤p のときは、
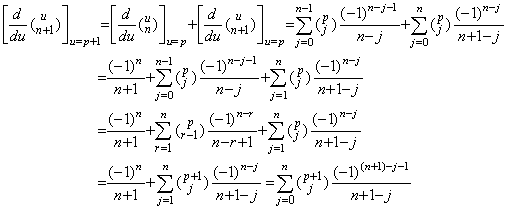 n>p のときは、
n>p のときは、
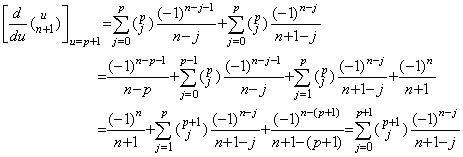 |
| [証明終] |
3.5 微分演算子
. .
(3.31)は t0 における微分係数 y0' を範囲 [t0, tp] の全ての等間隔点における関数値から得る公式である。tm における微分係数 ym' は範囲 [tm, tm+p] の全ての等間隔点の関数値を用いる公式により得ることが出来、添え字 0 の代わりに添え字 m を用いて(3.31)で表される。従って、
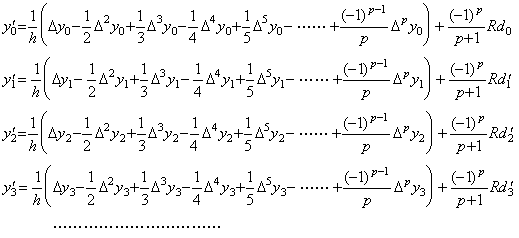 ここで、m≥1 に対する剰余項は ξ の値が(3.33)のそれとは異なるので Rdm' で表している。
ここで、m≥1 に対する剰余項は ξ の値が(3.33)のそれとは異なるので Rdm' で表している。
. .
上記の式から各階の階差を計算すると、
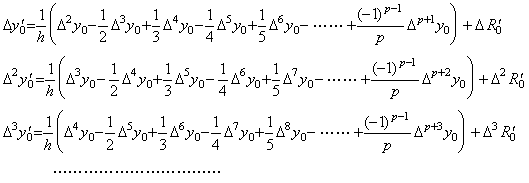
. .
しかし、階差 Δmy0' が m≥1 に対する Δp+my0 迄の階差の使用を必要とするなら、それらの高次階差が無視できないことを意味し、それらの高次階差は y0' の表記にも用いられるべきである。逆にいえば、関数値 y0' が Δpy0 迄の階差で表されればよいのであるから、式 Δmy0' の右辺の Δpy0 より高階の階差は剰余項に含めるべきである。これは、ベクトルは Δpy0 迄の要素からなり、m≥1 に対する高階の階さは Δp+my0→0 でなければならないというベクトル Y0 の定義からも明らかである。正確には、その証明は(3.33)の両辺の逐次階差をそれぞれに計算することにより行われる。故に、Y0 と Y0' の関係は同じ範囲 [a, b] における関係として表せることになる。
. .[定理 3.10]. .(3.33)の剰余項の m 階の階差を ΔmR0 で表すと、0≤m≤p−1 なら、
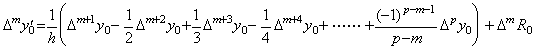
m=p なら、______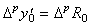 | (3.36) |
[証明]. .(3.33)の各式を一般形で表すと、
 と表せる。但し、定理 3.7 により、m≥1 且つ k≥2 に対して amk=am−1k−1+am−1k の関係があり、定理 3.9 により、m≥0 に対して am1=1 の関係がある。m 階の階差 Δmy0' はこれらの式の右辺の各項毎に m 階の階差を計算することにより得られる。それは各項の係数の m 階の階差を計算することに帰着する。但し、剰余項は ΔmR0と表す。
と表せる。但し、定理 3.7 により、m≥1 且つ k≥2 に対して amk=am−1k−1+am−1k の関係があり、定理 3.9 により、m≥0 に対して am1=1 の関係がある。m 階の階差 Δmy0' はこれらの式の右辺の各項毎に m 階の階差を計算することにより得られる。それは各項の係数の m 階の階差を計算することに帰着する。但し、剰余項は ΔmR0と表す。
| 1) | __m=0 なら(3.36)は(3.33)の第1式に同じである。
| | 2) | __m=1 なら Δy0 を持つ第1項は係数が Δa01=a11−a01=1−1=0 であるから階差 Δy0' =y1' −y0' から消える。k≥2 の各項の係数は Δa0k=a1k−a0k=a0k−1 であるから、m=0 の場合の k−1 の項の係数になる。故に、
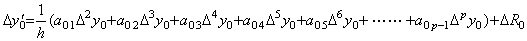 |
| 3) | __m=2 なら Δy0 を持つ第1項は係数が Δ2a01=a21−2a11+a01=1−2+1=0 であるから2階の階差 Δ2y0' =y2' −2y1' +y0' から消える。Δ2y0 を持つ第2項も係数が次のようになるから消える。
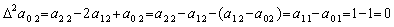 . .
k≥3 の各項の係数は m=1 の場合の k−1 項の係数になる。何故ならば、 . .
k≥3 の各項の係数は m=1 の場合の k−1 項の係数になる。何故ならば、
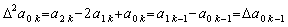 であるから。故に、
であるから。故に、
 |
| 4) | __(3.36)が m=n のとき成立するとすれば、Δny0 の項迄の係数は零になる。故に、
k≤n のとき、_____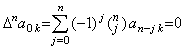 __________________ __________________
k>n のとき、. .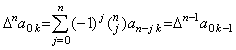 ___且つ、_______ ___且つ、_______
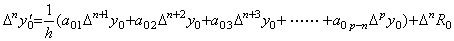 従って、m=n+1 のとき、
従って、m=n+1 のとき、
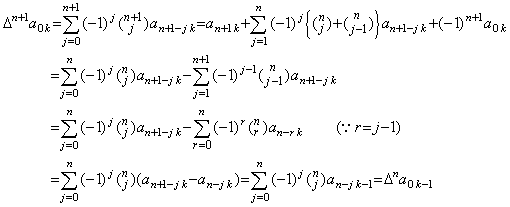 但し、仮定により k−1≤n のとき Δna0k−1=0 であるから、k≤n+1 のときは Δn+1a0k=0 である。故に、
但し、仮定により k−1≤n のとき Δna0k−1=0 であるから、k≤n+1 のときは Δn+1a0k=0 である。故に、
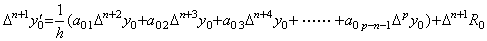 |
| 5) | __上の場合、整数 k は 1≤k≤p でなければならない。従って、n+1=p なら上式は、係数の添え字が p−n−1=0 となり Δky0 を持つ全ての項が消えてしまうから Δpy0' =ΔpR0 になる。
_________[証明終] |
. .
定理 3.10 により、関数 y と導関数 y' の両ベクトルの関係は行列演算(3.37)で表すことが出来る。p 階の階差 Δpy0' はベクトル ΔY0 の要素に依存しないからベクトル Y0' の要素には現れない。剰余項ベクトルの最後の要素 ΔpR0 もベクトル Y0' の Δpy0' 以外のどの要素にも影響を与えないから省略される。
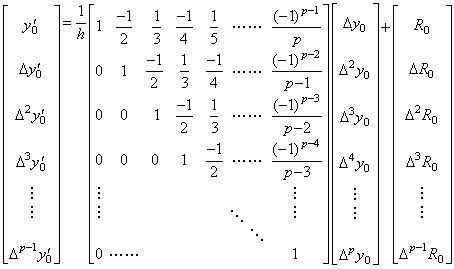 __(3.37). .
(3.37)の剰余項をベクトル R0 で表すと、ベクトル R0 は次の二つの関数の積の逐次階差である要素からなる。何故なら、(3.33)の剰余項は定理 3.8 における m=0, 1, 2, ……, p−1, p のそれぞれの場合における k=p+1 に対する係数を持つからである。従って、それぞれの関数を変換したベクトルの積で表せる。 __(3.37). .
(3.37)の剰余項をベクトル R0 で表すと、ベクトル R0 は次の二つの関数の積の逐次階差である要素からなる。何故なら、(3.33)の剰余項は定理 3.8 における m=0, 1, 2, ……, p−1, p のそれぞれの場合における k=p+1 に対する係数を持つからである。従って、それぞれの関数を変換したベクトルの積で表せる。
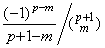 ______ ______
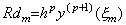 _____(3.38). .
左の m の関数の逐次階差は、定理 3.10 において p に p+1 を代入すれば Δp+1y0 の係数に等しい。何故なら、(3.33)において Δpy0 と Rdm の係数の関係においても定理 3.7 が成立するからである。故に、左の関数を変換したベクトルは(3.37)の行列の最後の列の p に p+1 を代入したものに等価である。従って、2つのベクトルの積の右側のベクトルを交換則により行列に展開すると、剰余項ベクトルは次のようになる。 _____(3.38). .
左の m の関数の逐次階差は、定理 3.10 において p に p+1 を代入すれば Δp+1y0 の係数に等しい。何故なら、(3.33)において Δpy0 と Rdm の係数の関係においても定理 3.7 が成立するからである。故に、左の関数を変換したベクトルは(3.37)の行列の最後の列の p に p+1 を代入したものに等価である。従って、2つのベクトルの積の右側のベクトルを交換則により行列に展開すると、剰余項ベクトルは次のようになる。
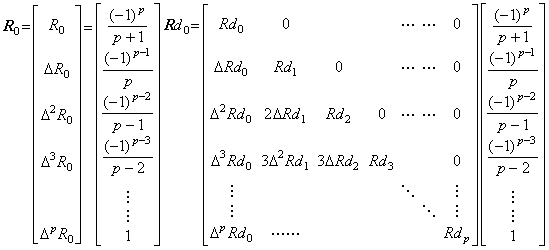 但し、(3.37)ではこれらベクトルの最後の要素は省略されている。
但し、(3.37)ではこれらベクトルの最後の要素は省略されている。
. .
ベクトルの大きさは行列展開した行列の主対角要素の絶対値の最大値である。故に、
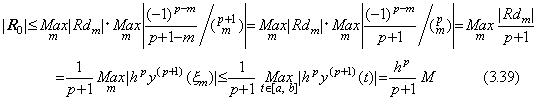 関数 y(t) をベクトル Y0 で表せるとき、条件 R0→0 は y(p+1)(t)≡0 又は h→0 により満足される。故に、p 階の階差 Δpy0' は定理 3.10 により Δpy0' =ΔpR0→0 を満たす。
関数 y(t) をベクトル Y0 で表せるとき、条件 R0→0 は y(p+1)(t)≡0 又は h→0 により満足される。故に、p 階の階差 Δpy0' は定理 3.10 により Δpy0' =ΔpR0→0 を満たす。
. .
ベクトル ΔY0 は演算子 Δ とベクトル Y0 の積に等価である。(3.37)の行列は各行が同じ要素を持ち、その上の行より1要素右にシフトされた上部三角行列である。これは第 2.3 節 階差演算子で述べた行列 A と同じ性質である。従って、(3.37)の行列を記号 D で表すと、行列 D と演算子 Δ の積は交換可能、即ち、DΔ=ΔD である。故に、(3.37)は記号的に(3.40)で表すことが出来る。
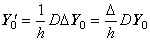 ______(3.40). .
ベクトル Y0 が零ならベクトル Y0' は零になる。しかし、ベクトル Y0 が零でない定数ベクトル、即ち、Y0=(y0, 0, 0, ……) でもベクトル Y0' は零になる。従って、行列 ΔD/h はベクトル Y0' と Y0 の商ではないが演算子である。故に、微分演算子である。行列 D も又演算子であり、微分演算子の演算子 Δ/h による商である。 ______(3.40). .
ベクトル Y0 が零ならベクトル Y0' は零になる。しかし、ベクトル Y0 が零でない定数ベクトル、即ち、Y0=(y0, 0, 0, ……) でもベクトル Y0' は零になる。従って、行列 ΔD/h はベクトル Y0' と Y0 の商ではないが演算子である。故に、微分演算子である。行列 D も又演算子であり、微分演算子の演算子 Δ/h による商である。
. .
結合則 D(ΔY0)=(DΔ)Y0 が(3.40)の中辺で実行されるとき、ベクトル Y0 は y0 から Δpy0 迄の p+1 個の要素を持つ。一方、階差ベクトル ΔY0 は Δy0 から Δpy0 迄の p 個の要素を持つ。上式の右辺は零と Δmy0 の積を(3.36)の括弧内の第1項として持つ式に等価である。故に、行列 DΔ は (p+1)2 個の要素を持ち、第1列と最後の行は全ての要素が零である。これは第 3.1 節 微分演算子の概略において述べた行列 ΔD である。
. .
従って、行列 D は (p+1)2 個の要素を持たねばならない。それらは(3.37)に示した行列の p2 個の要素とその最後の列の後ろに追加された列及び最後の行の下に追加され行の要素である。新しい最後の列は(3.41)に示された要素を持ち、新しい最後の行は最後の要素は1であるが、その他は全て零である。
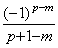 ______(3.41)
故に、ベクトル ΔY0 も p+1 個の要素を持たねばならない。その最後の要素は Δp+1y0=0 である。従って、この結合則の左辺は(3.41)と零の積を(3.36)の括弧の最後の項の後に追加した式に等価である。 ______(3.41)
故に、ベクトル ΔY0 も p+1 個の要素を持たねばならない。その最後の要素は Δp+1y0=0 である。従って、この結合則の左辺は(3.41)と零の積を(3.36)の括弧の最後の項の後に追加した式に等価である。
. .
行列 ΔD は行列 Δ と行列 D の積である。故に、(3.40)の最右辺は(3.41) と Δp+1y0 の積を(3.36)の括弧内の最後の項として持ち、記号 Δ を括弧の外に出した(3.42)の式に相当する。記号 Δ を括弧内に分配すると Δp+1y0=0 であるから最後の項は零になる。演算子 Δ は数値的な差分を表す記号 Δ とは異なるけれども、ベクトルの要素が記号的に Δky0 と表されるときは、演算子 Δ をベクトルに掛けることをスカラーとベクトルの通常の積とみなすことが出来る。
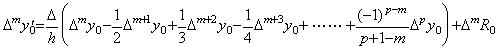 ____(3.42)
これらの関係は厳密に言えば階差演算子を使用するときは説明するべきであるが、結果において混乱は生じないから通常は省略してよい。従って、これらの関係は暗黙的に(3.40)で表す。 ____(3.42)
これらの関係は厳密に言えば階差演算子を使用するときは説明するべきであるが、結果において混乱は生じないから通常は省略してよい。従って、これらの関係は暗黙的に(3.40)で表す。
|
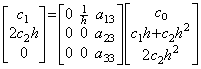 ___∴_
___∴_
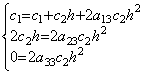 ___∴_
___∴_
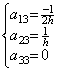
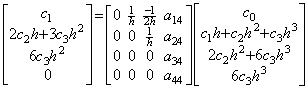 ___∴_
___∴_
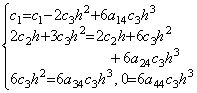
 . .
(3.5)は q が整数でも成立することは次のようにして示すことが出来る。或る整数 m に対して m<q<m+1 と仮定すると、関数 F(u) はこの近辺で概略 Fig. 3.1 で図示できる。関数 R は(3.3)により連続であるから、q→m に対する極限 R→Rm 及び ξ→ξm が存在して、
. .
(3.5)は q が整数でも成立することは次のようにして示すことが出来る。或る整数 m に対して m<q<m+1 と仮定すると、関数 F(u) はこの近辺で概略 Fig. 3.1 で図示できる。関数 R は(3.3)により連続であるから、q→m に対する極限 R→Rm 及び ξ→ξm が存在して、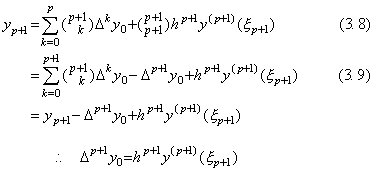 [証明終]
[証明終]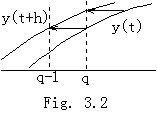
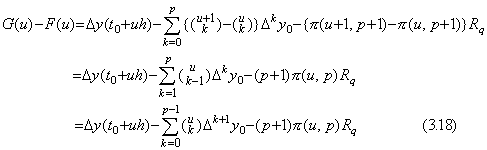

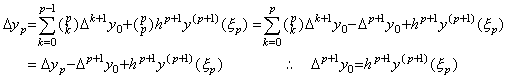
 ___(3.20)
___(3.20)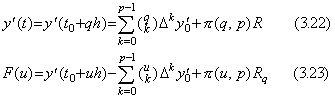
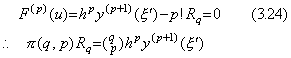
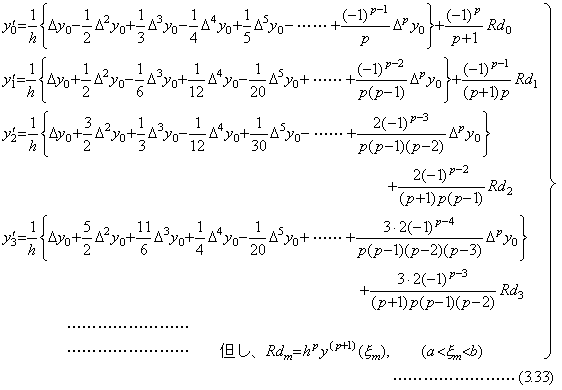
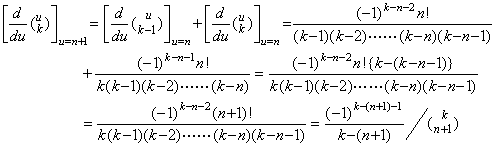 [証明終]
[証明終]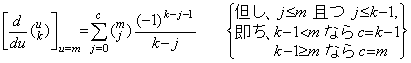 _____(3.35)
_____(3.35)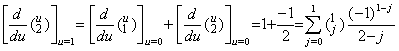
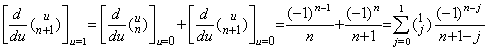

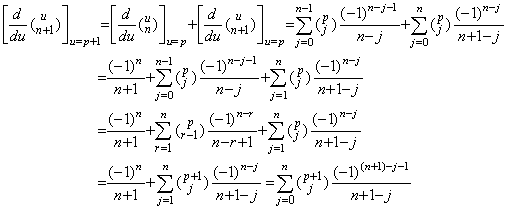
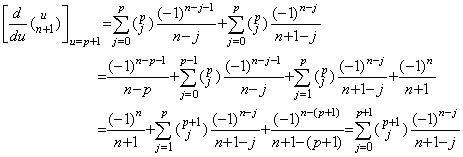
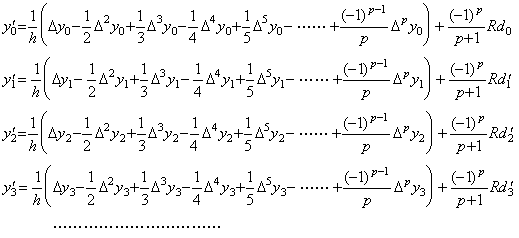
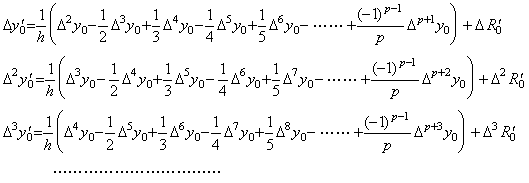
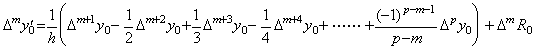
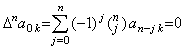 __________________
__________________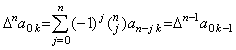 ___且つ、_______
___且つ、_______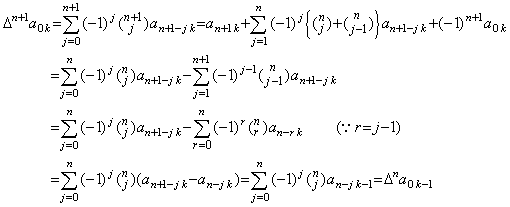
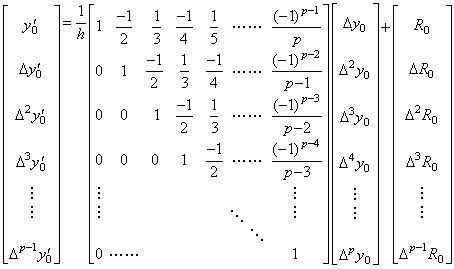 __(3.37)
__(3.37)
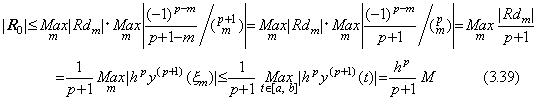
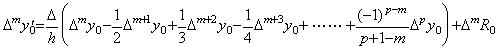 ____(3.42)
____(3.42)