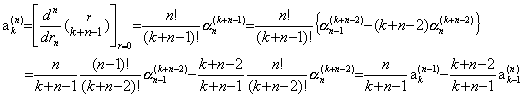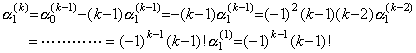|
3.6 2次微分演算子
. .
関数 y(t) が y(t)∈Cp+1[a, b] であるとき、導関数は y' (t)∈Cp[a, b] であり、Newton の補間公式(3.21)で表されねばならない。何故なら、剰余項が零になる等間隔区分点は y(t) の公式は p+1 点あるが t0 から tp−1 迄の p 点に減ずるからである。同様に、2次導関数は y"(t)∈Cp−1[a, b] であり、剰余項が零になる等間隔区分点は t0 から tp−2 迄の p−1 点に減ずる。従って、次のように Newton の補間公式で表される。
. .[定理 3.11]. .y"(t)∈Cp−1[a, b] のとき、t=t0+qh∈[a, b] を満たす任意の実数 q に対して、
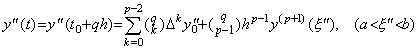 ____(3.43)
[証明]. .定理 3.1 の証明において y(t) 及び p にそれぞれ y"(t) 及び p−2 を代入すると、(3.3)及び残差(3.4)の F(u) は次のようになる。 ____(3.43)
[証明]. .定理 3.1 の証明において y(t) 及び p にそれぞれ y"(t) 及び p−2 を代入すると、(3.3)及び残差(3.4)の F(u) は次のようになる。
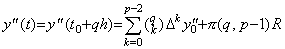 ________(3.44) ________(3.44)
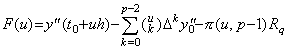 ________(3.45)
残差 F(u) は u=0, 1, 2, ……, p−2 及び q の p 点で零になる。故に、p−1 次の微係数は Rolle の定理によりこれらの点の最大値と最小値の間のある点で零になる。その点を ξ"=t0+uh とすると、 ________(3.45)
残差 F(u) は u=0, 1, 2, ……, p−2 及び q の p 点で零になる。故に、p−1 次の微係数は Rolle の定理によりこれらの点の最大値と最小値の間のある点で零になる。その点を ξ"=t0+uh とすると、
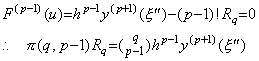 この剰余項は q の値が整数の場合も成立する。その証明は(3.6)において述べたのと同様に行われる。_________________________[証明終]
この剰余項は q の値が整数の場合も成立する。その証明は(3.6)において述べたのと同様に行われる。_________________________[証明終]
. .
定理 3.2 の証明と同様に、p−1 階の階差 Δp−1y0" は次のように剰余項だけを持つ公式で表される。
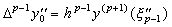 ________(3.46)
|y(p+1)(t)|≤M が満たされるとき、p−1 階の階差は h→0 に対して Δp−1y0"→0 が成立し、2次導関数 y"(t) は p−2 次関数により十分な精度で近似できる。従って、次のようにベクトルで表される。 ________(3.46)
|y(p+1)(t)|≤M が満たされるとき、p−1 階の階差は h→0 に対して Δp−1y0"→0 が成立し、2次導関数 y"(t) は p−2 次関数により十分な精度で近似できる。従って、次のようにベクトルで表される。
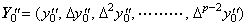 ________(3.47)
ベクトル Y0" と Y0' の関係は(3.21)に示した y' (t) の Newton の補間公式を微分して得なければならない。その微分は(3.23)に示した残差 F(u) を用いて間接的に行わなければならない。 ________(3.47)
ベクトル Y0" と Y0' の関係は(3.21)に示した y' (t) の Newton の補間公式を微分して得なければならない。その微分は(3.23)に示した残差 F(u) を用いて間接的に行わなければならない。
. .[定理 3.12]. .y' (t)∈Cp[a, b] のとき、t=t0+mh∈[a, b] を満たす任意の整数 m に対して、
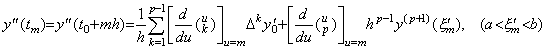 _____(3.48)
[証明]. .導関数 y' (t) と m<q<m+1 を満たす実数 q 以外においては近似剰余項を持つ補間公式の間に(3.23)で示される残差 F(u) が存在する。これを変数 u により微分すると、その導関数は k=0 の項は消え、Rq の値は変数 u に対して定数であるから(3.49)で表される。 _____(3.48)
[証明]. .導関数 y' (t) と m<q<m+1 を満たす実数 q 以外においては近似剰余項を持つ補間公式の間に(3.23)で示される残差 F(u) が存在する。これを変数 u により微分すると、その導関数は k=0 の項は消え、Rq の値は変数 u に対して定数であるから(3.49)で表される。
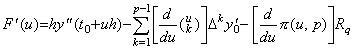 ______(3.49)
残差 F(u) は点 q の近辺で Fig. 3.1 に類似の図で表される。従って、微分係数 F' (u) は m<q1<q を満たす或る q1 に対して零になる。その点 q1 は q→m に対して q1→m になり、q に関する関数列 F(u) は連続であるから ξ' →ξm' 且つ F' (m)=0 を満たす ξm' が存在する。ここで、Rq の値は(3.24)により次のように与えられる。 ______(3.49)
残差 F(u) は点 q の近辺で Fig. 3.1 に類似の図で表される。従って、微分係数 F' (u) は m<q1<q を満たす或る q1 に対して零になる。その点 q1 は q→m に対して q1→m になり、q に関する関数列 F(u) は連続であるから ξ' →ξm' 且つ F' (m)=0 を満たす ξm' が存在する。ここで、Rq の値は(3.24)により次のように与えられる。
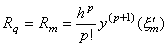 _______________[証明終] _______________[証明終]
. .
(3.48)の係数は定理 3.6, 3.7, 3.8 及び 3.9 が成立するから、定理 3.10 は y0", y0' 及び p−1 を y0' , y0 及び p のそれぞれに代入した場合にも成立する。従って、(3.48)の逐次階差は次のように表される。
0≤m≤p−2 なら、
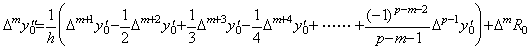
及び、m=p−1 なら、____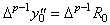 ________________(3.50). .
この逐次階差を行列演算式で表すと次のようになる。 ________________(3.50). .
この逐次階差を行列演算式で表すと次のようになる。
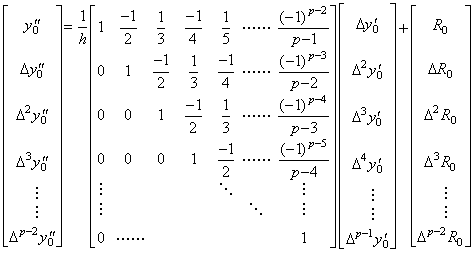 ___(3.51). .
(3.38) 及び (3.39)は y0", y0' 及び p−1 を y0' , y0 及び p のそれぞれに代入した場合にも ξm の値は異なるが成立する。従って、 ___(3.51). .
(3.38) 及び (3.39)は y0", y0' 及び p−1 を y0' , y0 及び p のそれぞれに代入した場合にも ξm の値は異なるが成立する。従って、
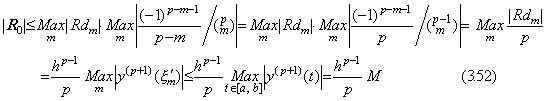 . .
関数 y' (t) がベクトルY0' で表せるとき、条件 R0→0 が y(p+1)(t)≡0 又は h→0 により満たされる。従って、(3.50)において p−1 階の階差は Δp−1y0"=Δp−1R0→0 を満たす。 . .
関数 y' (t) がベクトルY0' で表せるとき、条件 R0→0 が y(p+1)(t)≡0 又は h→0 により満たされる。従って、(3.50)において p−1 階の階差は Δp−1y0"=Δp−1R0→0 を満たす。
. .
(3.51)の行列は(3.37)の行列 D の最後の列と行を除いた要素からなる。しかし、この行列は行列 D と同じものであり、ベクトル ΔY0' の Δpy0' 及びそれより高階の階差の要素が h→0 に対して全て零になるという理由により最後の列と行は省略されているだけである。従って、(3.40)の最右辺をベクトル Y0' に代入すると、(3.51)は次のようになる。
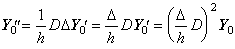 ______(3.53)
故に、著者は (ΔD/h)2 を2次微分演算子と呼ぶ。 ______(3.53)
故に、著者は (ΔD/h)2 を2次微分演算子と呼ぶ。
. .
この2次微分演算子は y(t) と y' (t) の Newton の補間公式を微分するという2段階の微分により得られた。これは y(t) の Newton の補間公式を一度で2次微分したものと同じでなければならない。その演算子は Δ2D2/h2 と表され、D2 として表された行列は積 D×D に等しい。これらは以下の定理により示される。
. .[定理 3.13]. .y(t)∈Cp+1[a, b] のとき、t=t0+rh∈[a, b] を満たす任意の実数 r に対して、
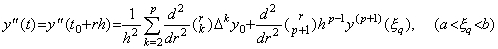 ___(3.54)
但し、ξq は y(t) の Newton の補間公式の或る点 t=t0+qh∈[a, b] に対する剰余項を与える値である。 ___(3.54)
但し、ξq は y(t) の Newton の補間公式の或る点 t=t0+qh∈[a, b] に対する剰余項を与える値である。
[証明]. .定数 Rq が(3.3)の剰余項の関数 R に代入されたとき、関数 y(t) とこの近似公式の残差 F(u) は(3.4)で表され、u=q の近傍では Fig. 3.1 で表された。微分係数 F' (u) は m<q1<q<q2<m+1 を満たす2点 q1, q2 で零になる。従って、(3.55)で表される2次微係数 F"(u) は q1<r<q2 を満たす或る点 r で零になる。
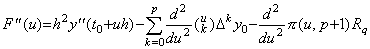 ____(3.55)
従って、その点 r において、 ____(3.55)
従って、その点 r において、
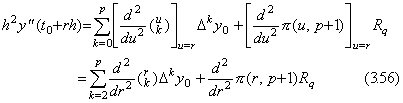 剰余項の定数 Rq は(3.5)で与えられるから、ξ を ξq で表せば、
剰余項の定数 Rq は(3.5)で与えられるから、ξ を ξq で表せば、
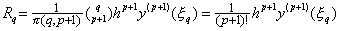 となる。故に、y"(t0+rh)は(3.54)で表される。___________________[証明終]
となる。故に、y"(t0+rh)は(3.54)で表される。___________________[証明終]
. .
F"(r)=0 となる点 r は q→m としても等間隔区分点 m にならない。何故なら、Fig. 3.1 を見れば明らかに 点 q1 は点 m に漸近するけれども点 q2 は区間 [m, m+1] の中間点に近づくだけだからである。点 q が点 m の左に来たとき、これらの点の関係は m−1<q<q1<m<q2<m+1 になり、点 r は点 m のあたりに近づくが点 m になるか定かでない。点 q が m+1 又は m+2 に漸近するなら、点 r は点 m+1 のあたりに近づくが点 m+1 になるか定かでない。しかし、F"(u)は y(t) とその近似補間公式の残差の2次微分であるから(3.55)により次の条件を満たす十分小さな値Mが存在する。
|F"(u)|≤Mh2≤h2|y"(t0+uh)|max________∴. .h→0 に対し、|F"(u)|→0
従って、等間隔区分点 m における2次微分係数は剰余項を Rm で表して次の式により表される。剰余項 Rm は h→0 のとき零に収束する。
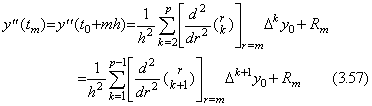
. .[定理 3.14]. .k≥1 のとき、
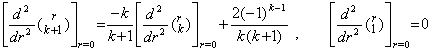 ____(3.58)
[証明]. .関数 f(r) と一次関数 g(r) の積を二回微分すると、 g"(r)≡0 により、 ____(3.58)
[証明]. .関数 f(r) と一次関数 g(r) の積を二回微分すると、 g"(r)≡0 により、
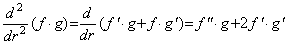 _____(3.59)
故に、 _____(3.59)
故に、
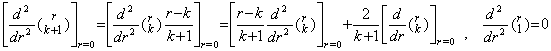 定理 3.6 により、
定理 3.6 により、
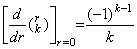 | [証明終] |
. .
従って、(3.57)の最右辺の係数は m=0 及び k≥1 について次のように順次に得られる。それらは、k=1 のとき1、k=2 のとき (−2/3)+(2/3)(−1/2)=−1、k=3 のとき (−3/4)(−1)+(2/4)(1/3)=11/12、k=4 のとき (−4/5)(11/12)+(2/5)(−1/4)=−5/6 等々である。
. .[定理 3.15] 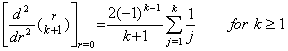 ______(3.60)
[証明]. .(3.59)の一次関数が g(r)=r なら、 ______(3.60)
[証明]. .(3.59)の一次関数が g(r)=r なら、
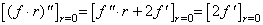 故に、
故に、
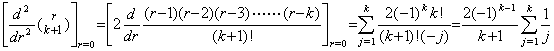
. .
[定理 3.16]. .m≥1 且つ k≥2 のとき、
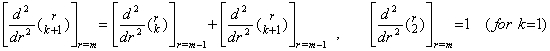 ____(3.61)
[証明] ____(3.61)
[証明]
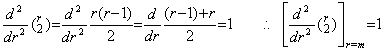 k≥2 のとき、r−1=u を代入すると、
k≥2 のとき、r−1=u を代入すると、
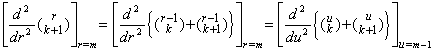
. .
[定理 3.17]. .m≥1 且つ k≥m+1 に対し、
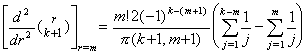 _____(3.62)
[証明]. .1). . m=1 なら、定理 3.15 により k≥2 のとき以下のように成立する。 _____(3.62)
[証明]. .1). . m=1 なら、定理 3.15 により k≥2 のとき以下のように成立する。
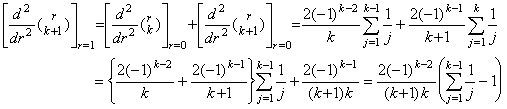 2). . m=n 且つ k≥n+1 のとき成立すると仮定すると、
2). . m=n 且つ k≥n+1 のとき成立すると仮定すると、
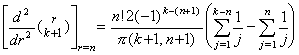 . .
m=n+1 且つ k≥n+2 のとき以下のように成立する。 . .
m=n+1 且つ k≥n+2 のとき以下のように成立する。
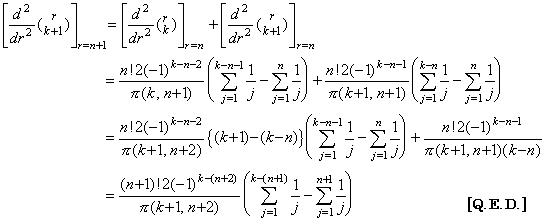
. .
従って、Newton の補間公式の2次導関数の t=t0 における値は(3.57)により次の第1公式で表される。その他の等間隔区分点における公式は上記の定理により以下のように逐次に得られる。ここで、中括弧内の最後の項の係数は(3.62)の k+1=p に対する値である。
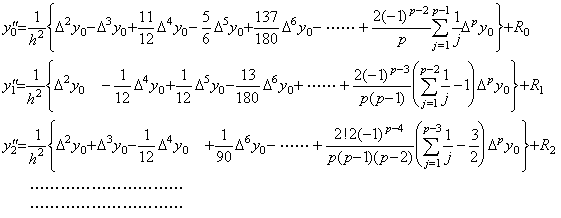 . .
y"(tm) の逐次階差は上記の式の右辺の逐次階差により得られる。それは同じ k の値を持つ Δk+1y0 の係数の逐次階差を得ることに帰着し、上記の第1式の係数を用いることにより(3.63)に帰着する。但し、m の値は p−2 以下であり、Δp−1y0"=Δp−1R0 が成立する。その証明は定理 3.10 の証明により容易に示される。何故なら、それは定理 3.7 に述べた係数の関係のみに依存し、定理 3.16 はそれと同じ関係だからである。 . .
y"(tm) の逐次階差は上記の式の右辺の逐次階差により得られる。それは同じ k の値を持つ Δk+1y0 の係数の逐次階差を得ることに帰着し、上記の第1式の係数を用いることにより(3.63)に帰着する。但し、m の値は p−2 以下であり、Δp−1y0"=Δp−1R0 が成立する。その証明は定理 3.10 の証明により容易に示される。何故なら、それは定理 3.7 に述べた係数の関係のみに依存し、定理 3.16 はそれと同じ関係だからである。
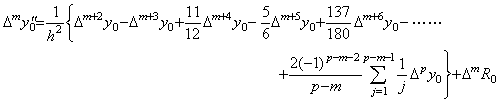 ___(3.63). .
(3.63)は次の行列演算式で表すことが出来る。 ___(3.63). .
(3.63)は次の行列演算式で表すことが出来る。
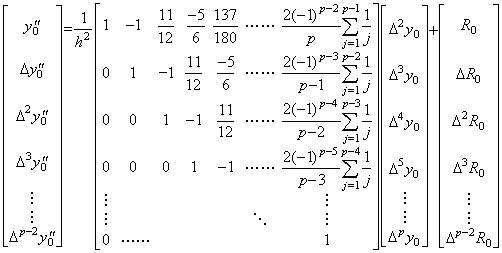 __(3.64). .
剰余項ベクトル R0 は次の二つの m の関数の積であり、k=p≥m+1 であるから 0≤m≤p−1 である。但し、j=1 から j=0 迄の和は零とする。 __(3.64). .
剰余項ベクトル R0 は次の二つの m の関数の積であり、k=p≥m+1 であるから 0≤m≤p−1 である。但し、j=1 から j=0 迄の和は零とする。
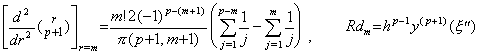 従って、
従って、
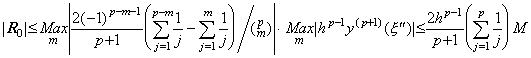 . .
条件 R0→0 は、関数 y(t) がベクトル Y0 で表せるとき、y(p+1)(t)≡0 又は h→0 であることにより成立する。従って、p−1 階の階差は Δp−1y0"=Δp−1R0→0 が成立する。 . .
条件 R0→0 は、関数 y(t) がベクトル Y0 で表せるとき、y(p+1)(t)≡0 又は h→0 であることにより成立する。従って、p−1 階の階差は Δp−1y0"=Δp−1R0→0 が成立する。
. .
ベクトル Δ2Y0 は演算子 Δ2 とベクトル Y0 の積に等価である。(3.64)の行列は全ての行が同じ要素を持ち、それらはすぐ上の行より1要素右にシフトしている上部三角行列である。従って、この行列を記号 D2 で表すと、行列 D2 と演算子 Δ2 の積は交換可能であり、次のようになる。
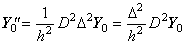 _______(3.65) _______(3.65)
. .
[定理 3.18]_____D2=D×D
[証明]. .演算子 D の第1行 k 列の要素を dk で表すと、演算子 D の第 k 列は次に示す縦ベクトルになる。
(dk, dk−1, dk−2, ………, d2, d1, 0, 0, ………)
故に、積 D×D の第1行 k 列の要素は次のようになる。
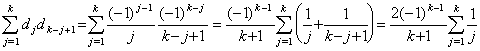 ____(3.66)
これは定理 3.15 で D2 として示した行列の第1行 k 列の要素に等しい。 ____(3.66)
これは定理 3.15 で D2 として示した行列の第1行 k 列の要素に等しい。
. .
演算子 D の第 j 行 k 列の要素を djk で表すと、それは k<j では零であり、k≥j では dk−j+1 である。故に、積 D×D の第 j 行 k 列の要素は、k<j の場合は、m<j に対しては djm=0 であり、m≥j に対しては dmk=0 であるから零である。k≥j の場合は次のようになる。
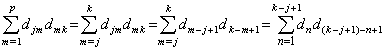 これは(3.66)により第1行 k−j+1 列の要素である。故に、積 D×D の第 j 行は第1行と j−1 要素右にシフトされている他は同じであり、積 D×D は行列 D2 に等しい。
これは(3.66)により第1行 k−j+1 列の要素である。故に、積 D×D の第 j 行は第1行と j−1 要素右にシフトされている他は同じであり、積 D×D は行列 D2 に等しい。
. .
演算子 D が p 次の正方行列であるから、積 D×D は p 次の正方行列である。一方、D2 で表される行列は(3.64)に示すように p−1 次の正方行列である。しかし、Δp+1y0→0 が成立し、Δp−1y0"→0 は剰余項にのみ依存するという理由により、第 p 行と第 p 列は表記を省略されているだけである。
3.7 高次微分演算子
. .
関数 y(t) が y(t)∈Cp+1[a, b] であるとき、n 次の導関数は y(n)(t)∈Cp−n+1[a, b] である。従って、それが Newton の補間公式で表されるとき、剰余項が零になる等間隔区分点は t0 から tp−n 迄の p−n+1 点に減少する。
. .[定理 3.19]. .y(n)(t)∈Cp−n+1[a, b]のとき、t=t0+qh∈[a, b]を満たす任意の実数 q に対して、
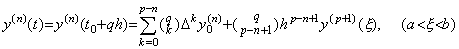 ___(3.67)
[証明]. .y(n)(t) の補間公式、及び、剰余項の R が q に対する値 Rq の定数である残差 F(u) は次のように表される。 ___(3.67)
[証明]. .y(n)(t) の補間公式、及び、剰余項の R が q に対する値 Rq の定数である残差 F(u) は次のように表される。
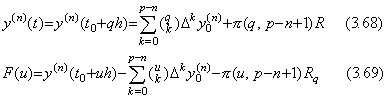 . .
残差 F(u) は u=0, 1, 2, ……, p−n 及び q の p−n+2 点で零になる。故に、p−n+1 次導関数は Rolle の定理によりこれらの点の最大値と最小値の間の或る点で零になる。その点を ξ=t0+uh とすると、 . .
残差 F(u) は u=0, 1, 2, ……, p−n 及び q の p−n+2 点で零になる。故に、p−n+1 次導関数は Rolle の定理によりこれらの点の最大値と最小値の間の或る点で零になる。その点を ξ=t0+uh とすると、
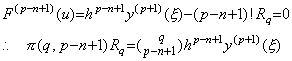 この剰余項は q が整数の場合も成立する。その証明は(3.6)で述べたのと同様に行われる。__[証明終]
この剰余項は q が整数の場合も成立する。その証明は(3.6)で述べたのと同様に行われる。__[証明終]
. .
定理 3.2 の証明と同様にして、p−n+1 階の階差は次のように剰余項だけの公式で表される。
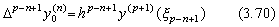 . .
|y(p+1)(t)|≤M が満たされるとき、p−n+1 階の階差は h→0 に対して Δp−n+1y0(n)→0 を満たし、n 次導関数 y(n)(t) は十分な精度で p−n 次関数で近似できる。従って、次のベクトルで表すことが出来る。 . .
|y(p+1)(t)|≤M が満たされるとき、p−n+1 階の階差は h→0 に対して Δp−n+1y0(n)→0 を満たし、n 次導関数 y(n)(t) は十分な精度で p−n 次関数で近似できる。従って、次のベクトルで表すことが出来る。
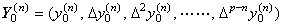 _____(3.71). .
n−1 次導関数 y(n−1)(t) は(3.67)の n に n−1 を代入することにより Newton の補間公式で次のように表される。 _____(3.71). .
n−1 次導関数 y(n−1)(t) は(3.67)の n に n−1 を代入することにより Newton の補間公式で次のように表される。
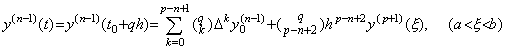 ___(3.72)
従って、ベクトルでは次のように表される。 ___(3.72)
従って、ベクトルでは次のように表される。
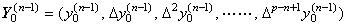 _____(3.73). .
y(n−1)(t) を微分すると、等間隔区分点における y(n)(tm) の値は定理 3.12 と同様の証明により y(n−1)(tm) の逐次階差で次のように表される。 _____(3.73). .
y(n−1)(t) を微分すると、等間隔区分点における y(n)(tm) の値は定理 3.12 と同様の証明により y(n−1)(tm) の逐次階差で次のように表される。
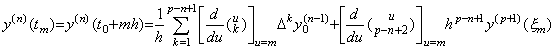
(a<ξm<b) | _____(3.74) |
. .
上記の公式の両辺の逐次階差は 0≤m≤p−n に対しては(3.75)で表され、m=p−n+1 に対しては Δp−n+1y0(n)=Δp−n+1R0 で表される。但し、ΔmR0 は(3.74)の剰余項を Rm で表してその逐次階差を表す。これは定理 3.6, 3.7, 3.8, 3.9 及び 3.10 により明らかである。
 _____(3.75). .
この逐次階差を行列演算式で表すと、 _____(3.75). .
この逐次階差を行列演算式で表すと、
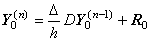 _____(3.76) _____(3.76)
. .
[定理 3.20]. .n 次微分演算子は
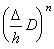 ________(3.77)
[証明]. .n=1 及び n=2 のとき成立することは既に示した。n−1 次微分演算子のとき成立するとすれば、(3.76)により、 ________(3.77)
[証明]. .n=1 及び n=2 のとき成立することは既に示した。n−1 次微分演算子のとき成立するとすれば、(3.76)により、
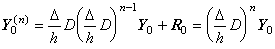 _____(3.78)
R0→0 の理由は、hp−n+1y(p+1)(ξm) を Rdm と置くと定理 3.8 により、 _____(3.78)
R0→0 の理由は、hp−n+1y(p+1)(ξm) を Rdm と置くと定理 3.8 により、
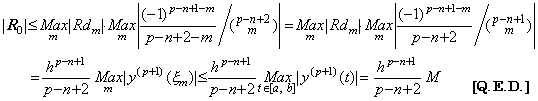
. .
(3.77)の n 次微分演算子は y(n−1)(t) の Newton の補間公式を微分することにより得られている。これは y(t) の Newton の補間公式を n 次微分することにより得られる演算子と同じであることを示さねばならない。
. .
[定理 3.21]. .y(t)∈Cp+1[a, b] 且つ 1≤n≤p のとき、t=t0+rh∈[a, b] なる任意の実数 r に対し、
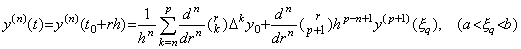 ___(3.79)
但し、ξq は y(t) の Newton の補間公式の或る点 t=t0+qh∈[a, b] における剰余項を与える値である。 ___(3.79)
但し、ξq は y(t) の Newton の補間公式の或る点 t=t0+qh∈[a, b] における剰余項を与える値である。
[証明]. .n=1 及び n=2 のとき成立することは既に示した。n−1 次導関数 y(n−1)(t) のときも成立すると仮定する。
. .
(3.4)に示した残差 F(u) の n−1 次導関数は(3.80)で表され、残差が p+2 点で零になるから n−1 次導関数は p−(n−1)+2 点で零になる。これらの点を uk(k=1, 2, ……, p−n+3) で表すと、F(n−1)(u) の導関数は uk と uk+1 の間の或る点で零になる。この点を r で表すと、r におけるこの導関数の値は(3.81)で表される。
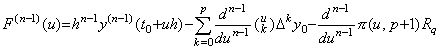 ____(3.80) ____(3.80)
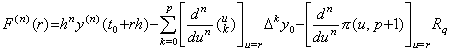 ____(3.81)
定数 Rq は(3.5)により次のように与えられる。 ____(3.81)
定数 Rq は(3.5)により次のように与えられる。
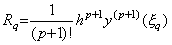
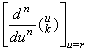 は は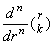 に同じであり、k<n に対しては零である。. .
導関数 F(n)(r) は上記の p-n+2 点以外では零にならない。しかし、F(n)(r) は y(t) とその近似公式との残差の n 次導関数であるから、(3.81)により次の条件を満たす十分小さな値 M が存在する。故に、(3.79)は任意の r について成立する。 に同じであり、k<n に対しては零である。. .
導関数 F(n)(r) は上記の p-n+2 点以外では零にならない。しかし、F(n)(r) は y(t) とその近似公式との残差の n 次導関数であるから、(3.81)により次の条件を満たす十分小さな値 M が存在する。故に、(3.79)は任意の r について成立する。
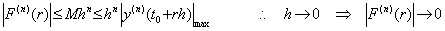 ____[証明終] ____[証明終]
. .
従って、等間隔区分点における n 次導関数の値は剰余項を Rm で表して次式で表される。
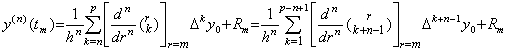 ___(3.82) ___(3.82)
. .
[定理 3.22]. .関数 f(r) と一次関数 g(r) の積の n 次導関数は、
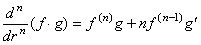 ______(3.83)
[証明]. .定理 3.14 により n=1 及び n=2 のときは明らかに成立する。 ______(3.83)
[証明]. .定理 3.14 により n=1 及び n=2 のときは明らかに成立する。
n=k のとき成立すると仮定すると、g"(r)≡0 により、
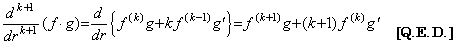
. .
[定理 3.23]. .m=0 のとき、(3.82)の k 番目の係数を ak(n) と表すと、
k≥1 且つ n≥2 に対して、
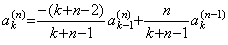 ,____a0(n)=0____(3.84)
[証明]. .k≥1 且つ n≥2 の場合は、(3.83)により、 ,____a0(n)=0____(3.84)
[証明]. .k≥1 且つ n≥2 の場合は、(3.83)により、
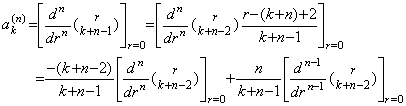
 は n−1 次関数であるからその n 次導関数は恒等的に零である。故に、 は n−1 次関数であるからその n 次導関数は恒等的に零である。故に、
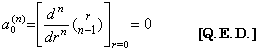
. .
これらの係数は p=10 の場合 Table 3.2 で表される。
Table 3.2___p=10 且つ m=0 の場合の(3.82)の k 番目の係数
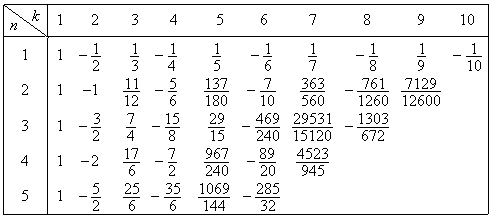
. .
[定理 3.24]. .(3.82)の k 番目の係数を amk と表すと、m=0 且つ任意の n に対しては Table 3.2 で表される。m≥1 and k≥2 に対しては、
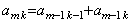 ,
但し、任意の m に対して am1=1____(3.85)
[証明]. .n=1 及び n=2 に対しては定理 3.7 及び 3.16 により示された。n−1 次導関数の場合に成立すると仮定すると(3.83)により、 ,
但し、任意の m に対して am1=1____(3.85)
[証明]. .n=1 及び n=2 に対しては定理 3.7 及び 3.16 により示された。n−1 次導関数の場合に成立すると仮定すると(3.83)により、
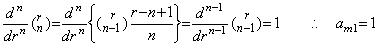 k≥2 の場合には r−1 を u と置くと、
k≥2 の場合には r−1 を u と置くと、

. .
[定理 3.25]. .(3.82)の剰余項の m 階の階差を ΔmR0 と表すと、
0≤m≤p−n のとき、
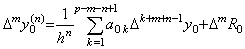 ,____ ,____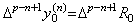 ____(3.86)
[証明]. .(3.82)を係数 amk で表すと、 ____(3.86)
[証明]. .(3.82)を係数 amk で表すと、
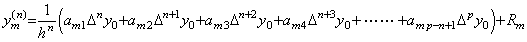 m 階の階差 Δmy0(n) は右辺の各項毎に係数の m 階の階差を計算することにより得られる。その結果は(3.86)になる。定理 3.24 により、その証明は定理 3.10 と、左辺には ym(n) があり、右辺の第1項には Δny0 があることを除いて同じである。
m 階の階差 Δmy0(n) は右辺の各項毎に係数の m 階の階差を計算することにより得られる。その結果は(3.86)になる。定理 3.24 により、その証明は定理 3.10 と、左辺には ym(n) があり、右辺の第1項には Δny0 があることを除いて同じである。
. .
故に、(3.86)を次の行列演算式で表すことが出来る。
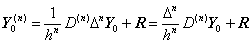 ______(3.87)
D(n) で表された行列は、k 番目の要素が a0k である第1行と、m 番目の行は k 番目の要素として a0k−m を持つ p−n 個の行からなる。但し、a0k−m は k≤m のときは零である。 ______(3.87)
D(n) で表された行列は、k 番目の要素が a0k である第1行と、m 番目の行は k 番目の要素として a0k−m を持つ p−n 個の行からなる。但し、a0k−m は k≤m のときは零である。
. .
剰余項は h→0 のとき R→0 になる。何故なら、(3.82)の剰余項の係数 amp−n+2 は、
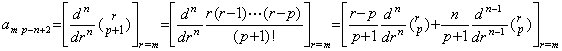 であり、
であり、
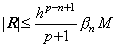 を満たす値 βn が存在するからである。但し、|y(p+1)(t)|≤M である。 を満たす値 βn が存在するからである。但し、|y(p+1)(t)|≤M である。
. .
[定理 3.26]. .D(n) で表される行列は D で表される演算子 n 個の積である。即ち、
D(n)=D×D×………×D
[証明]. .n=2 の場合は既に示した。D(n−1) の場合にも成立すると仮定すると、D(n)=D×D(n−1) を証明すればよい。(3.86)の k, m, a0k, R0 の代わりにそれぞれ j, k, aj(n), R(n) を使い、n に n−1 を代入すると、
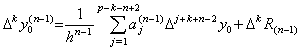 (3.75)の Δky0(n−1) にこれを代入し、剰余項を R0 の代わりに R(1) で表すと、
(3.75)の Δky0(n−1) にこれを代入し、剰余項を R0 の代わりに R(1) で表すと、
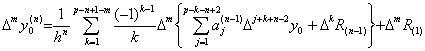 ____(3.88)
y(p+1)(t)≡0 と仮定すると、ΔkR(n−1), R(1) 及び R(n) を持つ項は消え、(3.88)は次のようになる。 ____(3.88)
y(p+1)(t)≡0 と仮定すると、ΔkR(n−1), R(1) 及び R(n) を持つ項は消え、(3.88)は次のようになる。
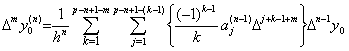 _____(3.89)
j+k−1+m>p−n+1 となるような j と k の値があり、それらの階差は Δpy0より高階である。これらの階差は剰余項の一部であり、仮定により消える。j+k−1+m を i で置き換え、その他の項を i=1, 2, 3, ……… の順に Δi により並べ替えると、m=0 の場合には、 _____(3.89)
j+k−1+m>p−n+1 となるような j と k の値があり、それらの階差は Δpy0より高階である。これらの階差は剰余項の一部であり、仮定により消える。j+k−1+m を i で置き換え、その他の項を i=1, 2, 3, ……… の順に Δi により並べ替えると、m=0 の場合には、
- i=1 なら k=1 且つ j=1 でなければならない。従って、Δ の係数は下式の 1) である。これは D の第1行と、D(n−1) の第1列の積である。
- i=2 なら(k=1, j=2) 及び (k=2, j=1) である。従って、Δ2 の係数は下式の 2) である。これは D の第1行と、D(n−1) の第2列の積である。
- i=3 なら (k=1, j=3), (k=2, j=2) 及び (k=3, j=1) である。従って、Δ3 の係数は下式の 3) である。これは D の第1行と、D(n−1) の第3列の積である。
- 同様にして、 i=p−n+1 なら k=1∼(p−n+1) に対して j=(p−n+1)∼1 である。従って、Δp−n+1 の係数は下式の 4) である。これは D の第1行と、D(n−1) の第 p−n+1 列の積である。
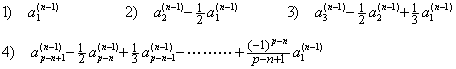 . .
m=1 の場合には、i=1 なら j+k=1 であるから k 及び j の値は存在しない。従って、Δ の係数は零である。これは D の第2行と、D(n−1) の第1列の積である。i=2 なら j と k の値は上記箇条書き第1項の場合であり、Δ2 の係数は上式の 1) である。これは D の第2行と、D(n−1) の第2列の積である。i=3 なら j と k の値は上記箇条書き第2項の場合であり、Δ3 の係数は上式の 2) である。これは D の第2行と、D(n−1) の第3列の積である。i=4 なら j と k の値は上記箇条書き第3項の場合であり、Δ4 の係数は上式の 3) である。これは D の第2行と、D(n−1) の第4列の積である。i=p−n+1 なら j+k=p−n+1 であるから k=1∼(p−n) に対して j=(p−n)∼1 である。従って、Δp−n+1 の係数は下式になる。これは D の第2行と、D(n−1) の第 p−n+1 列の積である。 . .
m=1 の場合には、i=1 なら j+k=1 であるから k 及び j の値は存在しない。従って、Δ の係数は零である。これは D の第2行と、D(n−1) の第1列の積である。i=2 なら j と k の値は上記箇条書き第1項の場合であり、Δ2 の係数は上式の 1) である。これは D の第2行と、D(n−1) の第2列の積である。i=3 なら j と k の値は上記箇条書き第2項の場合であり、Δ3 の係数は上式の 2) である。これは D の第2行と、D(n−1) の第3列の積である。i=4 なら j と k の値は上記箇条書き第3項の場合であり、Δ4 の係数は上式の 3) である。これは D の第2行と、D(n−1) の第4列の積である。i=p−n+1 なら j+k=p−n+1 であるから k=1∼(p−n) に対して j=(p−n)∼1 である。従って、Δp−n+1 の係数は下式になる。これは D の第2行と、D(n−1) の第 p−n+1 列の積である。
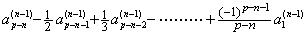 . .
m≤p−n である任意の m の場合は、i が m 以下なら j+k−1+m≤m 、即ち、j+k≤1 であるから k 及び j の値は存在しない。従って、これらの Δi の係数は零である。これは D の第 m+1 行と、D(n−1) の第 i 列の積である。 i=m+1 なら j 及び k の値は上記箇条書き第1項の場合であり、Δm+1 の係数は上式の 1) である。これは D の第 m+1 行と、D(n−1) の第 m+1 列の積である。同様にして、i=p−n+1 なら j+k=p−n+2−m であるから k=1∼(p−n+1−m) に対して j=(p−n+1−m)∼1 である。従って、Δp−n+1 の係数は下式になる。これは D の第 m+1 行と、D(n−1) の第 p−n+1 列の積である。 . .
m≤p−n である任意の m の場合は、i が m 以下なら j+k−1+m≤m 、即ち、j+k≤1 であるから k 及び j の値は存在しない。従って、これらの Δi の係数は零である。これは D の第 m+1 行と、D(n−1) の第 i 列の積である。 i=m+1 なら j 及び k の値は上記箇条書き第1項の場合であり、Δm+1 の係数は上式の 1) である。これは D の第 m+1 行と、D(n−1) の第 m+1 列の積である。同様にして、i=p−n+1 なら j+k=p−n+2−m であるから k=1∼(p−n+1−m) に対して j=(p−n+1−m)∼1 である。従って、Δp−n+1 の係数は下式になる。これは D の第 m+1 行と、D(n−1) の第 p−n+1 列の積である。
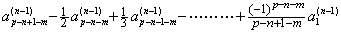 . .
y(p+1)(t) が恒等的に零ではないとき、Newton の補間公式は関数 y(t) を tp+1 より低次の部分と残りの2つの部分に分ける。その微分は低次の部分には Δpy0 より高階の階差を生じないし、残りの部分は h→0 により消える。故に、D(n)=D×D(n−1) は y(t)∈Cp+1[a, b] なる関数について常に成立する。 . .
y(p+1)(t) が恒等的に零ではないとき、Newton の補間公式は関数 y(t) を tp+1 より低次の部分と残りの2つの部分に分ける。その微分は低次の部分には Δpy0 より高階の階差を生じないし、残りの部分は h→0 により消える。故に、D(n)=D×D(n−1) は y(t)∈Cp+1[a, b] なる関数について常に成立する。
. .
従って、任意の m に対する Δi の係数は一般的に(3.90)で表される。
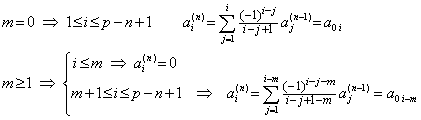 _____(3.90)
これらの係数を用い、且つ、i−m の代わりに k を用いると(3.89)は次のようになる。 _____(3.90)
これらの係数を用い、且つ、i−m の代わりに k を用いると(3.89)は次のようになる。
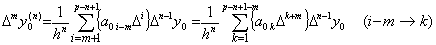 これは剰余項のない(3.86)に同じである。
これは剰余項のない(3.86)に同じである。
. .
[定理 3.27]
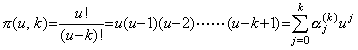 _____(3.91) _____(3.91)
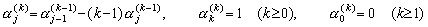 ____(3.92)
(第一種 Stirling 数)
[証明]. .π(u,0)=1 であるから α0(0)=1 は明らかである。k≥1 なら、 ____(3.92)
(第一種 Stirling 数)
[証明]. .π(u,0)=1 であるから α0(0)=1 は明らかである。k≥1 なら、
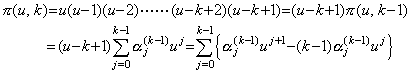 uk の係数を(3.91)と比較すると
uk の係数を(3.91)と比較すると
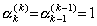 を得る。k≥1 に対して u0 を持つ項は存在しない。従って、α0(k)=0 である。その他の uj の係数に対して、 を得る。k≥1 に対して u0 を持つ項は存在しない。従って、α0(k)=0 である。その他の uj の係数に対して、
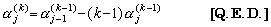
. .
(3.91)により(3.82)の中辺の係数は t=t0 において Stirling 数で次のように表される。何故なら、r=0 に対しては j=n の場合だけが存在するからである。
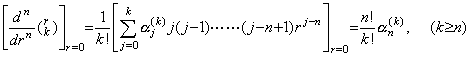 ____(3.93)
j<n に対しては rj−n の項は存在しないから k<n に対する係数は零である。従って、k に k+n−1 を代入すると新しい k の値は k+n−1≥n であるから k≥1 となり、 m=0 における(3.82)の最右辺の係数を得る。これに(3.92)を代入すると次に示すように定理 3.23 が得られる。 ____(3.93)
j<n に対しては rj−n の項は存在しないから k<n に対する係数は零である。従って、k に k+n−1 を代入すると新しい k の値は k+n−1≥n であるから k≥1 となり、 m=0 における(3.82)の最右辺の係数を得る。これに(3.92)を代入すると次に示すように定理 3.23 が得られる。
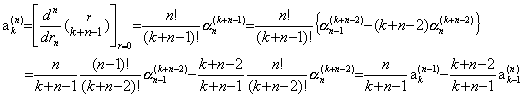 . .
n=1 の場合には、(3.93)の j の値は j=1 であり、Stirling 数は次式で表されるので(3.30)が得られる。 . .
n=1 の場合には、(3.93)の j の値は j=1 であり、Stirling 数は次式で表されるので(3.30)が得られる。
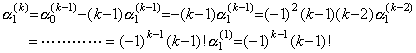 . .
j>1 に対する Stirling 数を簡単な公式で表すことは容易でない。しかし、以下に示すように Table 3.3 を用いることにより簡単に計算できる。j=k の欄に αj(k)=1 をセットし、k≥1 の欄に α0(k)=0 をセットすれば、j<k に対する αj(k) は(3.92)により得られる。 . .
j>1 に対する Stirling 数を簡単な公式で表すことは容易でない。しかし、以下に示すように Table 3.3 を用いることにより簡単に計算できる。j=k の欄に αj(k)=1 をセットし、k≥1 の欄に α0(k)=0 をセットすれば、j<k に対する αj(k) は(3.92)により得られる。
. .
Table 3.3 及び(3.93)を用いることにより、演算子 Dn の第1行 k 列の要素を計算することが出来る。但し、j 及び k の値はそれぞれ Table 3.2 の n 及び k+n−1 である。例えば、Table 3.2 の n=5 且つ k=6 の係数は次のように求まる。
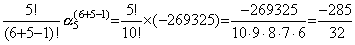
 Return to CONTENTS
Return to CONTENTS
|
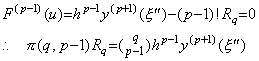
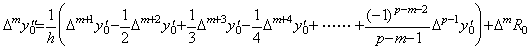
 ___(3.51)
___(3.51)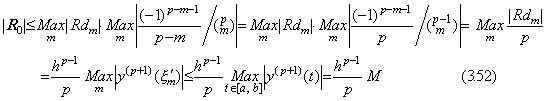
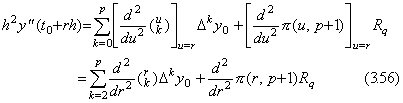
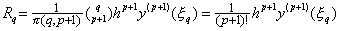
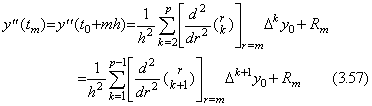
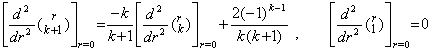 ____(3.58)
____(3.58)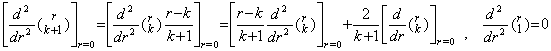
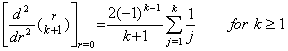 ______(3.60)
______(3.60)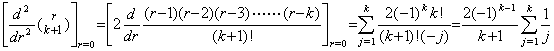
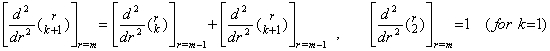 ____(3.61)
____(3.61)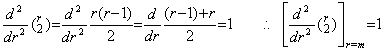
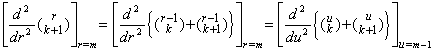
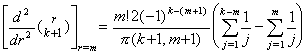 _____(3.62)
_____(3.62)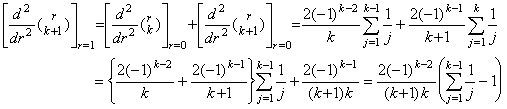
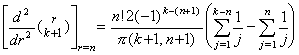
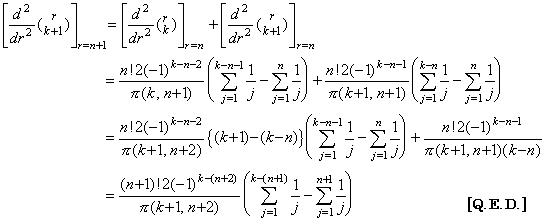
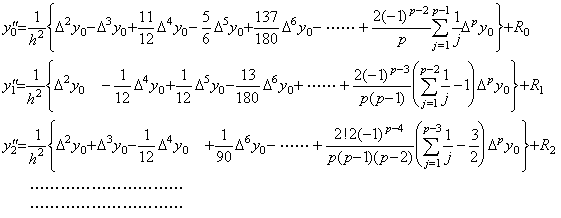
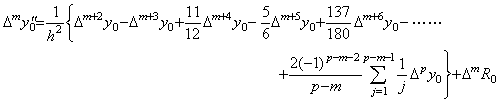 ___(3.63)
___(3.63)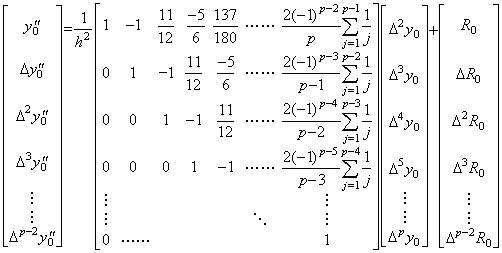 __(3.64)
__(3.64)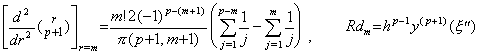
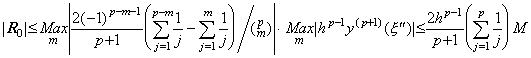
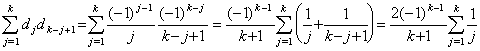 ____(3.66)
____(3.66)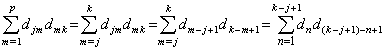
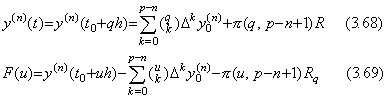
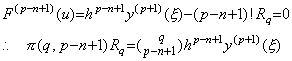
 _____(3.75)
_____(3.75)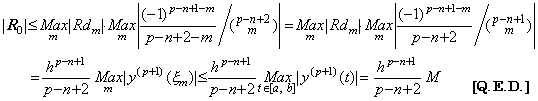
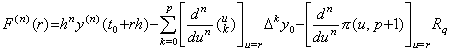 ____(3.81)
____(3.81)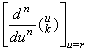 は
は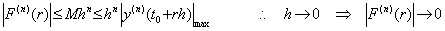 ____[証明終]
____[証明終]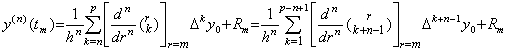 ___(3.82)
___(3.82)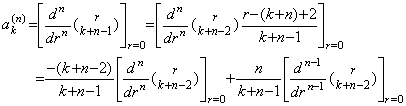
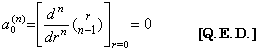


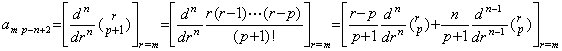
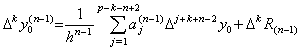
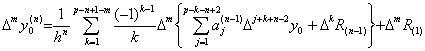 ____(3.88)
____(3.88)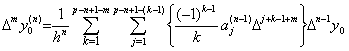 _____(3.89)
_____(3.89)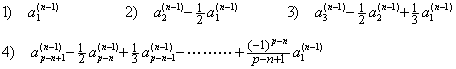
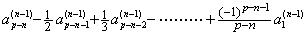
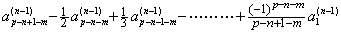
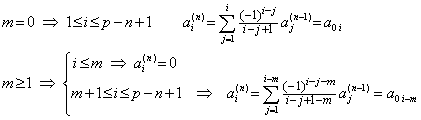 _____(3.90)
_____(3.90)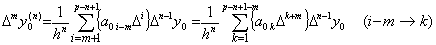
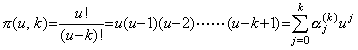 _____(3.91)
_____(3.91)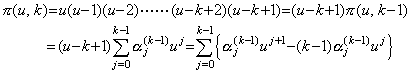
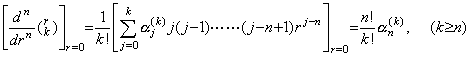 ____(3.93)
____(3.93)