2. 演算子法の超並列処理システム
2.1 ベクトルの加減算の超並列処理
. .
ベクトルの加減算は要素毎の加減算であるから各要素を個別のプロセッサに割当てれば並列処理ができる。各プロセッサに対応するベクトル要素を同時に与えるにはデータのビット数×プロセッサ数のデータバスを必要とする。従って、ハード及びソフト上の制約からプロセッサ数は余り多くできない。これを解決するにはデータのビット幅の共有データバス上に全てのプロセッサを並べ、ベクトル要素の値はy0,Δy0,Δ2y0,……の順に逐次的に与える。このデータを受取る権利は、最初は先頭のプロセッサにあり、y0を受取ると権利を2番目のプロセッサに渡す。2番目のプロセッサはΔy0を受取ると権利を3番目のプロセッサに渡す。この様にして全ての要素が受取られ、要素の終了記号を受けると最後のプロセッサは権利を失い、最初のプロセッサが権利を得る。同様にして、演算すべき2要素を受取ったプロセッサは演算を開始する。データ転送はメモリ読出し速度で可能であるから、その遅れは浮動小数点演算の時間に比べれば短く、最後のプロセッサがその担当の要素の計算を終えるまでの時間内に全ての要素の計算が終了し、実質的に並列演算となる。加減算ではベクトル要素をx0とy0,Δx0とΔy0のように組にして与えてもよい。
. .
プロセッサの結合を入出力ポートに変更すれば、データバスは局所ROM/RAM専用にできる。入出力ポートはポート番号0と1の2個を用意し、各プロセッサの入出力ポート0を前のプロセッサの入出力ポート1に接続する。これにより各プロセッサはクロック同期動作の必要がなく、データを受取る権利の受渡しも必要なくなる。各プロセッサは入出力ポート0を監視し、あるいは割込みにより最初のデータを取込み、その後はポート0のデータをポート1に転送する。ベクトル要素の終了記号を受けたプロセッサは次のベクトルの要素の受取り動作に入り、データが揃えば演算を開始する。この間、後続のプロセッサのためのデータ転送も並行して行う。これらの動作は各プロセッサの局所ROMにプログラムされ、全て同じプログラムである。
. .
これが本書の超並列処理のハード及びファームウェアの基本構想であり、一般的には以下のように構成される。
| 1. | 全てのプロセッサは同じハードウェア及びソフトウェア又はファームウェアを持つ。 |
| 2. | 各プロセッサのハードウェアは制御ユニット,ALU, ROM, RAM, 数個の入出力ポートより成る。 |
| 3. | 各プロセッサは入出力ポート0を前のプロセッサのポート番号0以外の一つの入出力ポートに接続することにより相似的構造に結合され、先頭のプロセッサのみが外部と入出力を行う。 |
| 4. | 上記主結合の他に2つの入出力ポートを用いて近隣のプロセッサ同士を結合することによりグループを構成することができる。 |
| 5. | 各プロセッサは一つの内部状態をRAMに記録保持し必要ならスタックに積むことができる。 |
| 6. | 各プロセッサは入出力ポート0からのデータを内部状態と比較し、内部状態として保持するか、何番の入出力ポートに出力するかを判断する。内部状態として保持する場合は元の内部状態をスタックに積むか何番のポートに出力するかを判断しそれらの結果を実行する。 |
| 7. | 各プロセッサは入出力ポート0からのデータ要求に対し内部状態を出力するか、他の入出力ポートにデータを要求し内部状態に基づく演算を実行して出力する。 |
. . 各プロセッサのROMに格納されるソフトウェアは上記の5,6,7項に記された作業を行うための動作をプログラムしたものであり、従来のプログラミングにおける与えられた問題を解くアルゴリズムではない。アルゴリズムに含まれる基本的な作業である。BASICでは、配列変数x, yに格納されたベクトルの加算を次のように記述する。但し、Δk−1x0, Δk−1y0は数値を表す。
| 10 FOR K=1 TO 10:X(K)=Δk−1x0:NEXT:FOR K=1 TO 10:Y(K)=Δk−1y0:NEXT |
| 20 FOR K=1 TO 10:Z(K)=X(K)+Y(K):NEXT |
この作業を本超並列処理で行う場合、Kの値はプロセッサの位置を表し、10行はK番目のプロセッサに各ベクトルのK番目の要素の値を与え、20行はK番目のプロセッサが2つの要素を加算して内部状態にセットすることである。従って、データのそろったプロセッサから演算を実行するためには10行の二つ目のFOR文は削除し、20行のFOR文にY(K)=Δk−1y0を挿入したBASICプログラムのKの値に対する作業をK番目のプロセッサが実行する。但し、Kの値はプロセッサのアドレス指定に等価であるので本システムでは使用しない。データは(2.1)の左から順に先頭のプロセッサに入力される。
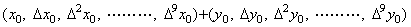 _______(2.1)
_______(2.1)
| . .[ベクトルの加算の動作規則] | |
|---|---|
| 1. | ポート0の入力が“(”ならそれを内部状態とする。 |
| 2. | ポート0の入力が数値の場合、内部状態が“(”ならそれをスタックに積み、コピーをポート1に出力して入力を内部状態とする。内部状態が“,”ならそれをスタックに積んで入力を内部状態とする。 |
| 3. | 内部状態が数値ならポート0の入力を全てポート1に出力する。 |
| 4. | ポート0の入力が“,”又は“)”の場合、内部状態が“(”ならそれをポート1に出力し、入力を内部状態とする。 |
| 5. | 内部状態が“)”なら“(”以外のポート0の入力を全て無視する。 |
| 6. | ポート0の入力が“+”ならポート1に出力し、内部状態をALUのアキュムレータにロードしてスタックされた内部状態をポップする。 |
| 7. | 再び、1から5迄の動作規則により、2個目のベクトル要素を得たプロセッサはポート1への他のデータ転送と平行して加算動作に入る。 |
| 8. | 加算を終えたプロセッサは結果を内部状態にセットする。 |
| 9. | ポート0に結果の出力要求を受けたとき、内部状態が“)”でないなら要求をポート1に出力し、スタックされた内部状態、計算結果の内部状態、ポート1の入力の順にポート0に出力する。内部状態が“)”ならそれをポート0に出力する。 |
| 10. | “)”をポート0に転送すれば動作を終了する。 |
. . データ(2.1)が左から順に先頭のプロセッサに入力されると、先頭のプロセッサは動作規則1により“(”を内部状態にセットする。x0の入力で動作規則2により“(”をスタックに積みコピーをポート1に送りx0を内部状態にセットする。以後、動作規則3を実行する。2番目のプロセッサは“(”“,”Δx0を受けて動作規則1, 4, 2, 3の順に動作し、“,”をスタックに積みΔx0を内部状態にセットする。同様にして10番目のプロセッサは“(”“,”Δ9x0を受けて“,”をスタックに積みΔ9x0を内部状態にセットする。11番目のプロセッサは“(”“)”を受けて動作規則4により“)”を内部状態にセットし動作規則5を実行する。それよりも10ステップ前に先頭のプロセッサは“)”の転送を完了しており、“+”の入力により動作規則6, 7, 8を実行し、第一要素の加算結果z0=x0+y0を内部状態にセットする。ベクトルYの要素終了記号“)”をポート1に転送後再度“+”が入力されれば再度動作規則6, 7, 8を実行するが、結果の出力要求の場合は動作規則9により、スタックの“(”と内部状態z0をポート0に出力し、2番目のプロセッサからホート1に送られてくる“,”とΔz0を転送する。同様にして“,”とΔ9z0を転送した後11番目のプロセッサが出力した“)”を転送して終了する。
. . データ(2.1)の“+”を“−”に変えればベクトルの減算が実行される。プロセッサの機能は全て同じでプロセッサにはアドレスがないから、どれかのプロセッサが故障した場合には別のプロセッサと交換するか単にそれをバイパスするだけで故障は修復される。これは脳と同様な故障修復である。最後部にプロセッサを追加すれば扱えるベクトルの次元が増え、関数の近似次数を上げたことになるから計算精度が向上する。これは脳の思考能力の向上に相当する。本システムはデータの入力が無いときは相似構造であるが、データの入力により各プロセッサの実行している箇条と内部状態が異なり非相似構造となる。これは脳も死に至ればただの蛋白質であるのと類似である。
. .
 この超並列演算システムを使用する応用プログラムはベクトルの加算をX+Yまたはベクトルをx, yで表してx+yと記述すればよい。従って、ハードが超並列処理になっても並列化コンパイラというようなものを必要としない。この数式は後に述べる超並列解析により2分木を構成するプロセッサの内部状態としてFig. 2.1のように表される。各プロセッサは内部状態に基づく処理を実行する際、内部状態がX, Yのプロセッサはベクトルの値を得て内部状態が“+”のプロセッサに与え、内部状態が“+”のプロセッサはそれらを加算する。このとき、2分木を構成している入出力ポート以外のポートに接続された上記の超並列演算システムにデータ(2.1)を与える。複雑な数式の場合、その2分木は四則演算子を内部状態とする多くのプロセッサを必要とし、それらは上記の超並列演算システムを個別に持たなければならない。上記の超並列演算システムの並列処理度は余り高度ではないので、BASICで示したようなプログラムを各プロセッサのROMに持つことでハードの負担を軽くすることができる。しかし、後に述べる知識情報処理の超並列処理の重要なヒントを与えるので本節ではハードウェアでの構成について詳細に述べる。
2.2 関数のベクトル変換と逆変換
この超並列演算システムを使用する応用プログラムはベクトルの加算をX+Yまたはベクトルをx, yで表してx+yと記述すればよい。従って、ハードが超並列処理になっても並列化コンパイラというようなものを必要としない。この数式は後に述べる超並列解析により2分木を構成するプロセッサの内部状態としてFig. 2.1のように表される。各プロセッサは内部状態に基づく処理を実行する際、内部状態がX, Yのプロセッサはベクトルの値を得て内部状態が“+”のプロセッサに与え、内部状態が“+”のプロセッサはそれらを加算する。このとき、2分木を構成している入出力ポート以外のポートに接続された上記の超並列演算システムにデータ(2.1)を与える。複雑な数式の場合、その2分木は四則演算子を内部状態とする多くのプロセッサを必要とし、それらは上記の超並列演算システムを個別に持たなければならない。上記の超並列演算システムの並列処理度は余り高度ではないので、BASICで示したようなプログラムを各プロセッサのROMに持つことでハードの負担を軽くすることができる。しかし、後に述べる知識情報処理の超並列処理の重要なヒントを与えるので本節ではハードウェアでの構成について詳細に述べる。
2.2 関数のベクトル変換と逆変換. . 通常、数値計算で関数を扱う場合、等間隔点の関数値を扱うが、本演算子法ではそれらの逐次階差を要素とするベクトルを扱う。従って、関数値をベクトルに変換する必要がある。この変換演算子を“v”で表すと、超並列演算システムに入力されるデータは(2.1)のベクトルXがない形(2.2)で表すことができる。この変換を使用する応用プログラムはこの変換を関数v(y(t))と記述し、2分木解析はFig. 2.1のXを空にYを関数y(t)に“+”を変換演算子“v”に変えた2分木に構成する。y(t)を内部状態とするプロセッサは(2.2)の関数値を得、変換演算子“v”を内部状態とするプロセッサはそれを受取ってデータ(2.2)として超並列演算システムに送りベクトルに変換する。
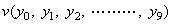 _____(2.2)
_____(2.2)
各プロセッサはこれと同様に自分の内部状態からひとつ前のプロセッサの内部状態を減算する。Kの値はプロセッサの位置を示し、Jのあたいは減算を実行するプロセッサの範囲の先頭プロセッサ位置を示す。従って、本システムではこれらの値は使用しない。前のプロセッサが後ろのプロセッサに自分の内部状態を送ることでこの演算を可能にする。
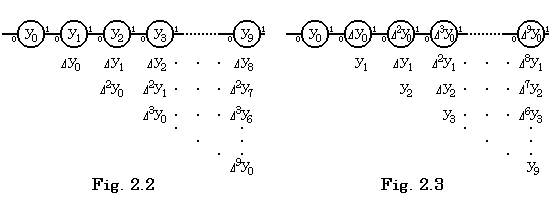
. . 先頭のプロセッサはデータ(2.2)の最後の“)”をポート0に受けるとポート1に転送し、続いて内部状態y0のコピーをポート1に出力する。2番目のプロセッサは“)”をポート0に受けるとポート1に転送し、続いて内部状態y1のコピーをポート1に出力し、更にポート0に受けるy0で内部状態をΔy0=y1−y0に変えコピーをポート1に出力する。3番目のプロセッサは“)”をポート0に受けるとポート1に転送し、続いて内部状態y2のコピーをポート1に出力し、ポート0に受けるy1で内部状態をΔy1=y2−y1に変えコピーをポート1に出力し、更に、ポート0に受けるΔy0で内部状態をΔ2y0=Δy1−Δy0に変えコピーをポート1に出力する。以下同様にしてK番目のプロセッサの内部状態にΔk−1y0がセットされる。この計算に要する時間は“)”が10番目のプロセッサに転送される時間と10番目のプロセッサが9回の減算を完了する時間の和であり、他のプロセッサの演算はこれと平行して行われる。各プロセッサの処理は下記の動作規則に基づく同一のプログラムで実行される。そのプログラムには何処を他のプロセッサと並行して実行すべきという指示は一切無いが並列処理が実行される。
| . .[関数値をベクトルに変換する動作規則] | |
|---|---|
| 1. | ポート0の入力“v”をポート1に出力し、ベクトル加算の動作規則1から5により関数値の一つを内部状態にセットする。 |
| 2. | ポート0の入力が“)”ならポート1に出力し、続いて内部状態のコピーをポート1に出力した後次の動作に入る。 |
| 3. | ポート0に数値の入力があれば内部状態から減算し、新しい内部状態のコピーをポート1に出力する。ポート0に数値入力が無くなれば終了する。 |
| 4. | ポート0に結果の出力要求を受けたならベクトル加算の動作規則9, 10により変換結果のベクトル値を出力する。 |
. . 通常、数値計算では計算結果はベクトルでなく関数値が要求される。ベクトルを関数値に変換する演算子を“r”で表すと、超並列演算システムに入力されるデータは(2.3)で表すことができる。この変換を使用する応用プログラムはこの変換を関数r(Y)と記述し、2分木解析はFig. 2.1のXを空に、演算子“+”を変換演算子“r”に変えた2分木に構成する。ベクトルYを内部状態とするプロセッサは(2.3)のベクトル値を得、変換演算子“r”を内部状態とするプロセッサはそれを受取ってデータ(2.3)として超並列演算システムに送りベクトルを関数値に変換する。
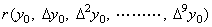 ______(2.3)
______(2.3)
2.3 ベクトルの積の超並列処理
. .
ベクトルの積W=XYは第3章1.4節の定理1.1に基づいてベクトルXを行列展開して(2.4)式で行う。
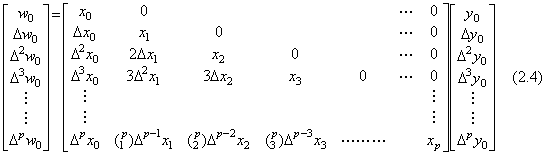
|
10 FOR J0=1 TO E2:G(J0)=X(J0):NEXT:FOR J0=1 TO E2:FOR J2=1 TO J0: __ J1=J0−J2+1:C(J2)=G(J1)*Y(J2):IF J1>1 THEN G(J1−1)=G(J1−1)+G(J1) 20 NEXT J2:IF J0>1 THEN FOR J2=2 TO J0:FOR J1=J0−J2+2 TO J0: __C(J1)=C(J1)+C(J1−1):NEXT J1,J2 30 W(J0)=C(J0):NEXT J0 |
. . この積を並列処理で計算可能にするためには配列Gは2次元配列を使い(2.4)式の行列から2項係数を除いた要素の値を計算しておかなければならない。BASICでは並列処理はできないが2次元配列を用いたプログラムは以下のように書ける。
| 10 FOR J0=1 TO E2:G(J0,1)=X(J0):NEXT:FOR J0=2 TO E2:FOR J1=2 TO J0: __ G(J0,J1)=G(J0−1,J1−1)+G(J0,J1−1):NEXT J1,J0 20 FOR J0=1 TO E2:FOR J1=1 TO J0:G(J0,J1)=G(J0,J1)*Y(J1):NEXT J1,J0 30 FOR J2=J0 TO 2:FOR J1=1 TO J2−1:G(J0,J1)=G(J0,J1)+G(J0,J1+1): __NEXT J1,J2,J0 |
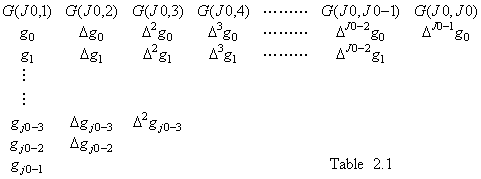
. . このシステムを使用する応用プログラムはベクトルの積をX×Y又はx×yと表し、2分木解析はFig. 2.1の"+"を"×"に変えた2分木に構成する。内部状態が"×"のプロセッサはXとYのベクトル値を受取って(2.5)のデータを超並列演算システムに転送して両者の積を計算する。超並列演算システムの第1列プロセッサはベクトルの加算の動作規則1から5によりベクトルXの各要素をそれぞれの内部状態にセットする。次に演算子"×"を受けるので積のプログラムへジャンプする。この演算子の転送を受けた他の行プロセッサも積のプログラムへジャンプする。そこでは先ずベクトルを差分表に展開する動作規則を実行する。
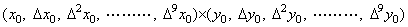 ______(2.5)
______(2.5)| . .[ベクトルを差分表に展開する動作規則] | |
|---|---|
| 1. | "×"をポート0に受けたプロセッサ(=Pj1)は内部状態が数値なら入力をポート1と3に転送し、内部状態のコピーをポート1に出力する。内部状態が")"なら無視する。 |
| 2. | "×"又は")"をポート2に受けたプロセッサ(=Pjk, k>1)はそれを内部状態にセットする。 |
| 3. | ポート0の入力が数値のとき、内部状態が数値ならそのコピーに入力を加算してポート3に出力する。内部状態が")"ならそのコピーをポート3に出力する。内部状態が"×"ならポート2の入力を待つ。 |
| 4. | ポート2の入力が数値のとき、内部状態が"×"ならそれをポート3に出力して入力を内部状態にセットし、コピーをポート1に出力する。続いてポート0の入力を調べる。 |
| 5. | ポート0又は2の入力が"("又は","ならベクトルの行列展開にベクトルを掛ける動作規則へ移行する。 |
. . 各プロセッサがこの動作規則により動作することによりその内部状態はFig. 2.5のようにセットされて差分表が構成される。差分表の最後の行の次の行プロセッサの内部状態は全て")"がセットされるが表記は省略されている。これはベクトルYを掛けるときその要素がこの行以降へ転送されるのを阻止する。ベクトルXの行列展開はこの差分表の各行に2項係数を掛けたものであるが、それはこの差分表の行列にベクトルYを掛けたとき各行の総和をTable 2.1の方法で求めることで行われる。

| . .[ベクトルの行列展開にベクトルを掛ける動作規則] | |
|---|---|
| 1. | ポート0の入力が"("又は","のとき、内部状態が数値なら内部状態をALUのアキュムレータにロードして入力を内部状態にセットする。内部状態が")"なら入力を無視する。 |
| 2. | ポート0の入力が数値のとき、内部状態が"("又は","ならポート1に出力し入力を内部状態にセットしコピーをポート1に出力しアキュムレータに内部状態を掛ける演算を開始する。内部状態が")"なら入力を無視する。 |
| 3. | 積の演算を開始したプロセッサは以後")"迄の全てのポート0の入力をポート3に転送する。積を完了したときは結果を内部状態にセットしコピーをポート2に出力する。但し、ポート2を使用していないプロセッサ(Pj1)はポート2への出力はしない。 |
| 4. | 内部状態が"×"ならポート2の入力を全てポート1に転送する。入力が")"のときは更にそのコピーをポート2に出力し内部状態をクリアする。 |
| 5. | 積の結果のコピーをポート2に出力したプロセッサはポート3の入力が数値なら内部状態に加算し結果の内部状態のコピーをポート2に出力する。ポート3の入力が")"ならポート2に転送し内部状態をクリアする。 |
| 6. | Pj1はポート3の入力が数値なら内部状態に加算しポート3の入力が")"ならベクトルの積の演算を完了する。 |
. . 動作規則3で演算を開始したプロセッサの内部状態は数値であるが、このときの入出力処理は動作規則1及び2とは異なるのでその区別のために動作状態というフラグを必要とする。このフラグは入出力のReadyフラグや割込み信号と同様にデータを表すものではないので特に必要が無い限り言及しない。入力が数値のときと記述すればReadyのときであることは明白であるように、積の演算を開始したプロセッサは以後・・・・と記述すれば動作状態フラグのセットは明白だからである。
. . 動作規則6でベクトルの積を完了した後、結果の出力要求に対してベクトルの加算の動作規則9, 10により結果を出力する。出力要求は"="を使用し、データ(2.5)の最後にこれを付ければ良い。ベクトルの加算や関数のベクトル変換の場合も同様である。
2.4 ベクトルの商の超並列処理
. .
ベクトルの商W=Y/XはベクトルXの行列展開の逆行列X−1が存在する場合はベクトルの積W=X−1Yで計算できるが、逆行列の計算を避けるためにXの行列展開Xを両辺に掛ければ商Wは連立一次方程式XW=Yの解として計算できる。第3章1.6節の定理1.6によりこの連立一次方程式は(2.6)式に変形して(2.7)式のように解くことができる。行列Xの対角要素のどれかが零のときはベクトルXの要素計算における区分点の取り方が適当でないか、ベクトルの定義域が適当でない。この対角要素による除算が必要なベクトルの商の要素は与えられていなければならない。そうでない場合はベクトルの商は確定しない。第4章3.2節のプログラムではこの場合常に零を与えているのでベクトルの商は一般的には正しくない。しかし、可変区分幅解法ではこのとき解は収束せず、区分幅が変わって行列Xの対角要素が零にならない範囲の正しい解に収束する。行列Xの対角要素に零がある場合はそれによる除算を実行しない方法でもよい。従って、ベクトルの商の超並列処理では行列Xの対角要素は零でないものとする。
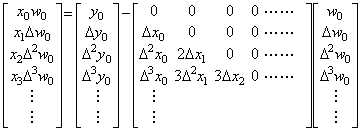 ____(2.6)
____(2.6)
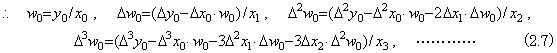
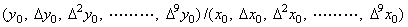 ____(2.8)
____(2.8). .
| . .[除数ベクトルを差分表に展開する動作規則] | |
|---|---|
| 1. | ポート0の入力が“/”のとき(=Pj1)、内部状態が数値なら入力をポート1と3に転送して内部状態をスタックに積み、内部状態が“)”なら内部状態をスタックに積む。 |
| 2. | “/”をポート2に受けたプロセッサ(=Pjk, k>1)はそれを内部状態にセットする。 |
| 3. | ポート0の入力が“(”ならベクトル加算の動作規則1から4により除数ベクトルの要素をそれぞれの内部状態にセットし(=Pj1)、最後の“)”をポート1に転送したプロセッサは内部状態の数値のコピーをポート1に出力する。その後、スタックの最上部が“(”なら(=P11)それをポート1と3に出力し商を計算する動作規則へ移行する。 |
| 4. | ポート0の入力が数値のとき、内部状態が数値ならそのコピーに入力を加算してポート3に出力する。内部状態が“)”ならそのコピーをポート3に出力する。内部状態が“/”ならポート2の入力を待つ。 |
| 5. | ポート2の入力が数値のとき、内部状態が“/”ならそれをポート3に出力して入力を内部状態にセットし、コピーをポート1に出力する。続いてポート0の入力を調べる。 |
| 6. | 動作規則4と5を終えた後、ポート0の入力が“(”ならポート1と3に、ポート2の入力が“(”ならポート3に転送し、商を計算する動作規則へ移行する。但し、内部状態が“/”ならポート2の入力“(”の転送を保留して商を計算する動作規則へ移行する。 |
. . 動作規則1から3により第1列プロセッサは内部状態をFig. 2.6(a)のようにスタックに積み、第1列及び第2列プロセッサは同図(b)のように内部状態をセットする。動作規則3及び4により第2列以降の内部状態は同図(c)から(d)となり差分表を完成する。
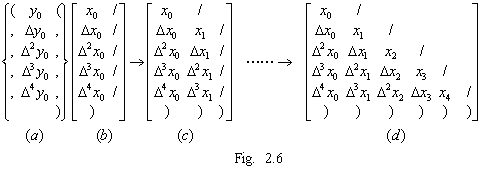
. . P22は“(”をポート0に受けることで自分が対角要素に在ることを知り、内部状態をスタックに積み内部状態に零をセットする。他の対角要素Pjjも同様に処理して同図(c)になる。{ }はスタックのデータを示す。Pj1(j>1)はw0と内部状態の積を終了すると結果をポート3に出力し、それぞれのスタックの“,”とΔj−1y0をポップしてポート3に出力する。P22はポート2に受けたw0Δx0を内部状態(=0)に加算し、“,”の次にポート2に受けるΔy0と結果の内部状態及びスタックのx1で(2.7)の第2式によりΔw0を計算する。Pj2(j>2)はポート0に転送されたΔw0をそれぞれの内部状態に掛け、結果のコピーをポート3に出力し、ポート2の数値を内部状態に加算してポート3に出力し、“,”とΔj−1y0をポート3に転送する。
. . P33はポート2のデータを全て内部状態(=0)に加算し“,”により加算データの終了を知り、次のΔ2y0と加算結果の内部状態及びスタックのx2で(2.7)の第3式によりΔ2w0を計算する。この計算における各行の要素に2項係数を掛けた総和は前節のTable 2.1に示した方法でデータの転送方向を逆にしたものであり、対角要素に結果が求まる。ここで第3行迄がFig. 2.7(e)のように確定し、以下同様にして同図(f)の対角要素に商のベクトル要素が求まる。この後、対角要素の内部状態を第1列プロセッサに転送する。同図の“∗”は内部状態は任意の値でよいことを示す。これらの処理を全てのプロセッサが同一のプログラムで行うための動作規則は下記のようになる。、
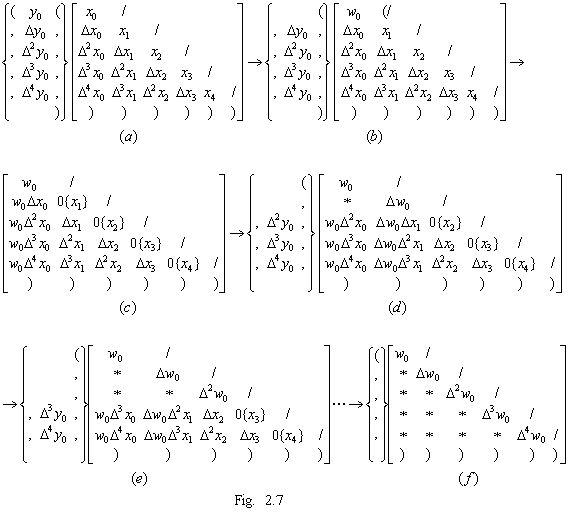
| . .[差分表から商を計算する動作規則] | |
|---|---|
| 1. | 内部状態が“/”ならポート2の入力“(”をポート1に転送し、ポート2の入力が“,”なら終了する。 |
| 2. | 内部状態が“)”ならポート0の入力“(”又は数値を無視する(読み捨てる)。又、スタックのデータが“)”ならそれを内部状態にポップする。 |
| 3. | スタックの最上部の“(”をポート1と3に出力したP11は次の数値データをアキュムレータにポップして内部状態で除算し、結果を内部状態にセットし、コピーをポート1に出力して終了する。 |
| 4. | ポート0の入力が“(”なら(=Pjj, j>1)内部状態をスタックに積んで内部状態に零をセットした後、ポート2の入力が数値なら全て内部状態に加算し、ポート2の入力が“,”なら加算を終了して入力“,”をポート3に転送し、次のポート2の数値から内部状態を減算し、スタックの数値をポップして除算し、結果を内部状態にセットしポート1と2に出力する。 |
| 5. | ポート0の入力が数値のとき、内部状態が数値なら入力をポート1に転送すると共に内部状態に掛け、結果を内部状態にセットし、コピーをボート3に出力する。その後、規則6を実行する。 |
| 6. | スタックの最上部が“,”のPj1(j>1)は“,”と次の数値をポップしてポート3に出力する。その後、ポート3の入力を内部状態にセットして終了する。その他のプロセッサはポート2の入力が数値なら内部状態に加算して結果のコピーをポート3に出力することを繰り返し、ポート2の入力が“,”なら加算を終了し、“,”と次にポート2に受ける数値をポート3に転送する。その後、ポート3に受ける数値をポート2に転送して終了する。 |
. . 上記動作規則により商の演算を終了した後、結果の出力要求“=”のポート0の入力に対してベクトルの加算の動作規則9, 10により結果を出力する。その後、各プロセッサの内部状態には不要なデータが残るが、演算開始時に必要な範囲は上書きされるので差し支えない。
2.5 ベクトルの微積分の超並列処理
. .
積分演算は(2.9)の(a)で表されるが、
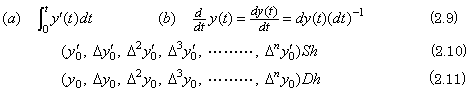
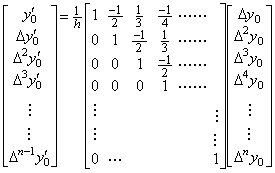 _____(2.12)
_____(2.12)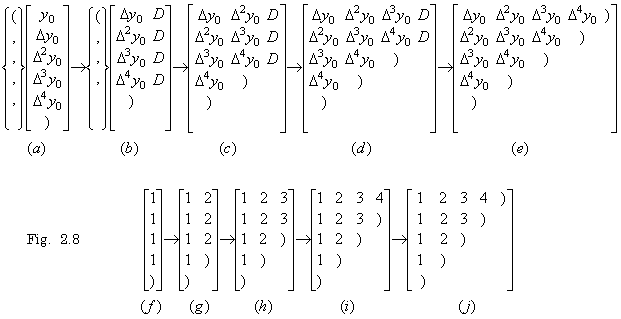
. . 微分行列の要素の分母を内部状態にセットしたプロセッサは上記のデータ転送と平行してスタックのベクトルの要素を内部状態で除算し、内部状態が偶数なら負符号をつけ、その計算が終了したら結果をポート2へ出力する。以後ポート3の入力をポート2に転送する。但し、ポート2を接続していない第一列プロセッサはポート3の入力を全て加算し、ポート3の入力が")"なら加算を終了してポート0の入力hで結果を除算する。以上で第1列プロセッサの内部状態に微分結果のベクトルの要素がセットされる。これらの処理を全てのプロセッサが同じプログラムで行うための動作規則は以下のようになる。
| . .[ベクトルを微分する動作規則] | |
|---|---|
| 1. | ベクトル加算の動作規則1から5を実行し、第1列プロセッサは被微分ベクトルの要素を内部状態にセットし次の演算子"D"の入力により以下の動作規則を実行する。但し、スタックのトップが"("であるP11はポート0への出力はしない。 |
| 2. | ポート0の入力が演算子"D"のとき、内部状態が")"ならそれをポート0に出力して終了し、内部状態が数値なら"D"をポート1と3に転送した後、内部状態をポート0に出力する(内部状態はクリアされる)。 |
| 3. | ポート1の入力が")"のとき、内部状態が空なら入力を内部状態にセットしてコピーをポート0に出力し、スタックをクリアし、ポート0の入力(=h)を読み捨てて終了する。内部状態が数値なら入力")"をポート0と3に転送する。 |
| 4. | ポート1の入力が数値(=ベクトルの要素)のとき、内部状態が空なら入力を内部状態にセットしてコピーをポート0に出力し、内部状態をスタックに積み、微分行列の要素1を内部状態にセットする。内部状態に微分行列の要素をセットしてから最初の入力なら入力をポート0と3に転送して、内部状態のコピーをポート3に出力し、以後、ポート1の入力をポート0と3に転送する。 |
| 5. | ポート2の入力が演算子"D"ならそれを内部状態にセットする。 |
| 6. | ポート2の入力が数値のとき、内部状態が"D"ならそれをポート3に出力して入力(=ベクトルの要素)を内部状態にセットする。内部状態がベクトルの要素ならそれをスタックに積んで入力に1を加えて(=微分行列の要素の分母)内部状態にセットする。内部状態が微分行列の要素の分母なら入力(=ベクトルの要素)をポート3に転送し続いて内部状態のコピーをポート3に出力し、その後はポート2の入力をポート3に転送する。 |
| 7. | ポート2の入力が")"のとき、内部状態が"D"なら入力")"を内部状態にセットしポート2に出力して終了し、内部状態が数値なら入力")"をポート3に転送する。 |
| 8. | 微分行列の要素の分母を内部状態にセットしたプロセッサは上記データ転送と平行してスタックの数値を内部状態で除算し、内部状態が偶数なら負符号を付加する計算を開始する。 |
| 9. | 計算を終えた後、ポート2を接続しているプロセッサは結果をポート2に出力し、以後、ポート3の入力をポート2に転送し、")"をポート2に転送したら終了する。ポート2を接続していない第1列プロセッサは計算結果を内部状態にセットし、ポート3のデータを内部状態に加算し、ポート3の入力が")"なら加算を終了し、ポート0の入力(=h)をポート1に転送すると共に内部状態を除算して終了する。 |
. . 積分演算は(2.13)で表され、2次元配列プロセッサにより超並列演算ができる。微分演算との違いは被演算ベクトルを差分に変換しないことと行列の要素の違いである。行列の要素は第3章第4節の定理4.8によりFig. 2.8(j)の内部状態から(2.14)により超並列計算できる。ここでは簡単化のために(2.15)に示す第1行の各要素の値を計算したものを全てのプロセッサがROMに格納しておき、内部状態がnのプロセッサはn番目の値を使用する。従って、積分演算の動作規則は微分演算の動作規則の一部を変更するだけで下記のようになる。
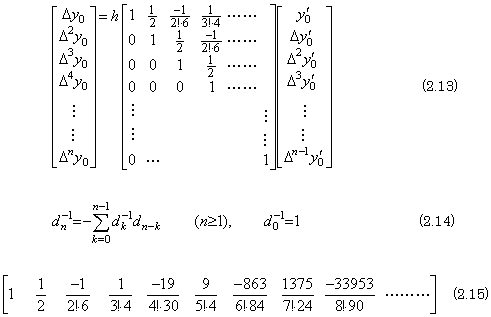
| . .[ベクトルを積分する動作規則] | |
|---|---|
| 1. | ベクトル加算の動作規則1から5を実行し、第1列プロセッサは被積分ベクトルの要素を内部状態にセットし次の演算子"S"の入力により以下の動作規則を実行する。但し、スタックのトップが"("であるP11はポート0への出力はしない。 |
| 2. | ポート0の入力が演算子"S"のとき、内部状態が")"ならそのコピーをポート0に出力して最後のポート0の入力(=h)を読み捨てて終了し、内部状態が数値なら"S"をポート1と3に転送した後、内部状態のコピーをポート0に出力し、内部状態をスタックに積み、内部状態に積分行列の要素番号1をセットする。 |
| 3. | ポート1の入力が")"なら入力")"をポート0と3に転送する。 |
| 4. | ポート1の入力が数値(=ベクトルの要素)のとき、積分行列の要素番号1を内部状態にセットした後最初の入力なら入力をポート0と3に転送して内部状態のコピーをポート3に出力する。その後は入力をポート0と3に転送する。 |
| 5. | ポート2の入力が演算子"S"ならそれを内部状態にセットする。 |
| 6. | ポート2の入力が数値のとき、内部状態が"S"ならそれをポート3に出力して入力(=ベクトルの要素)を内部状態にセットする。内部状態がベクトルの要素ならそれをスタックに積んで入力に1を加えて(=積分行列の要素番号)内部状態にセットする。内部状態が積分行列の要素番号なら入力(=ベクトルの要素)をポート3に転送し続いて内部状態のコピーをポート3に出力し、その後はポート2の入力をポート3に転送する。 |
| 7. | ポート2の入力が")"のとき、内部状態が"S"なら入力")"を内部状態にセットしポート2に出力して終了し、内部状態が数値なら入力")"をポート3に転送する。 |
| 8. | 積分行列の要素番号を内部状態にセットしたプロセッサは上記データ転送と平行してスタックの数値に要素番号の示す積分行列の要素の値をかける計算を開始する。 |
| 9. | 計算を終えた後、ポート2を接続しているプロセッサは結果をポート2に出力し、以後、ポート3の入力をポート2に転送し、")"をポート2に転送したら終了する。ポート2を接続していない第1列プロセッサは計算結果を内部状態にセットし、ポート3のデータを内部状態に加算し、ポート3の入力が")"なら加算を終了し、ポート0の入力(=h)をポート1に転送すると共に内部状態に掛けて終了する。 |
. .
積分演算終了後、ポート0の入力が結果の出力要求"="ならベクトルの加算の動作規則9と10により第1列プロセッサは内部状態を出力する。このときの出力は差分ベクトルΔYであり初期値y0を含んでいない。初期値が与えられているとき、これを含む結果を出力するには第1列プロセッサは内部状態を一つ後ろに移して(2.16)で表されるベクトル加算をしなければならない。ベクトルの加算の動作規則ではこの点に触れていないが、差分の次数の異なるベクトルを加算する場合には内部状態をシフトして両ベクトルの要素の位置合わせを行わねばならない。
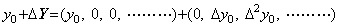 ______(2.16)
______(2.16)2.6 演算子の積の超並列処理
. . 微積分演算子以外の一般の演算子とベクトルの積、更に、任意の行列XとベクトルYの積W=XYもFig. 2.4の超並列システムで並列処理ができる。微積分演算もこの方法により処理することができる。微積分演算子は要素の性質及びベクトルとの積の計算法から行ベクトルの集まりと考えることもできるが、ベクトルの行列展開も演算子であり、その第1列がベクトルに等しいことから演算子は列ベクトルの集まりと考える。列ベクトルは転置して、カンマで区切った各要素を“( )”で括って表したので、行列はそれらの列ベクトル全体を“[ ]”で括って(2.17)のように1次元的に表す。従って、この行列とベクトルの積は(2.18)のデータを超並列演算システムに与えて計算する。
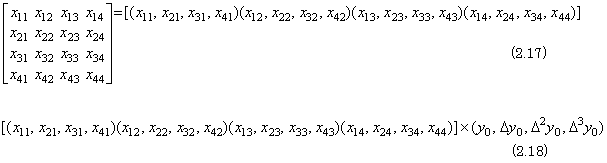
. . 次にP11は行列の終了記号“]”と積の演算子“×”を受けて転送し、これを受けた全てのプロセッサは2.3節ベクトルの積とは異なる積のプログラムを実行する。第1行プロセッサはベクトル要素の開始記号“(”又は要素の区切り記号“,”を受けて内部状態をスタックに積み、ポート0又は2の最初の数値入力を内部状態にセットしてその後の入力をポート3に転送することによりFig. 2.9(b)の第1行のように各内部状態をセットする。内部状態に数値をセットしたプロセッサはそのコピーをポート1に出力し、これをポート0に受けたプロセッサは内部状態をスタックに積んで入力を内部状態にセットし、そのコピーをポート1に出力する。その結果、各プロセッサはFig. 2.9(b)のようにそれぞれの内部状態をセットし、スタックの行列の要素と内部状態の積を計算し、結果をポート2に出力し、ポート3の入力をポート2に転送する。但し、ポート2を接続していない第1列プロセッサは積の結果を内部状態にセットし、ポート3の入力をすべてこれに加算する。これにより、行列とベクトルの積の要素が第1列プロセッサの内部状態にセットされる。これらの処理を全てのプロセッサが同じプログラムで処理するための動作規則は以下のようになる。
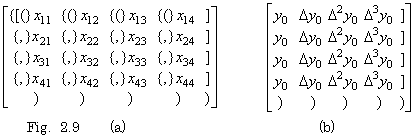
. .
| . .[行列を読込む動作規則] | |
|---|---|
| 1. | 各プロセッサはポート0の入力が行列開始記号“[”ならこれを内部状態とする。ポート0を接続していない第1行プロセッサはポート2の入力をポート0の入力とみなす。このポート2を含めたポート0を意味するときポート0(ポート2)と表記する。 |
| 2. | 各列プロセッサはベクトルを加算する動作規則1から5により対応する列要素を内部状態にセットする。但し、内部状態が“[”でポート0(ポート2)の入力が列開始記号“(”なら、入力“(”を内部状態にセットする際、入力がポート0からの場合は(=P11)内部状態“[”をスタックに積み、ポート2からの場合は(=P11以外の第1列プロセッサ)内部状態“[”を捨てる。 |
| 3. | ポート0(ポート2)の入力が列開始記号“(”のとき、列終了記号“)”をポート1に転送した後なら(=第1行プロセッサ)“[”をポート3に出力してから入力“(”及び以後の行列終了記号“]”までの入力をポート3に転送する。 |
| 4. | ポート0(ポート2)の入力が行列終了記号“]”のとき、内部状態が行列開始記号“[”ならそれをポート1に出力して入力“]”を内部状態にセットし、ポート2に接続されたプロセッサの内部状態のコピーを要求する。ポート2の応答が列終了記号“)”ならそれを内部状態にセットし、そうでないなら内部状態のコピーをポート1に出力する。 |
| 5. | ポート0(ポート2)の入力が演算記号“×”ならベクトルを掛ける動作規則へ移行する。 |
| . .[行列にベクトルを掛ける動作規則] | |
|---|---|
| 1. | 各プロセッサはポート0又はポート2の入力が演算記号“×”のとき、内部状態が数値ならスタックに積んで内部状態に入力をセットし、演算記号“×”がポート0の入力ならポート1と3に、ポート2の入力ならポート3にコピーを転送する。内部状態が“]”又は“)”なら入力を読み捨てる。 |
| 2. | ポート0(ポート2)の入力が“(”のとき、内部状態が“×”なら(=P11)入力を内部状態にセットしてスタックの“[”を捨てる。 |
| 3. | ポート0(ポート2)の入力が“,”のとき、内部状態が“×”なら入力を読み捨てる。内部状態が数値なら入力をポート3に転送する。 |
| 4. | ポート0(ポート2)の入力が数値のとき、内部状態が“(”又は“×”なら入力を内部状態にセットし、コピーをポート1に出力する。内部状態が数値なら入力をポート3に転送する。内部状態が“)”なら入力を読み捨てる。 |
| 5. | 内部状態に数値をセットしたプロセッサはデータ転送と平行して内部状態にスタックの数値を掛ける計算を開始し、完了したらポート2に結果を出力し、スタックをクリアし、ポート3の入力をポート2に転送する。但し、ポート2を接続していない第1列プロセッサはポート3の入力を全て内部状態に加算し、ポート3の入力が“]”なら加算を終了する。 |
| 6. | ポート0又はポート2の入力が“)”のとき、内部状態が数値なら入力をポート3に転送する。内部状態が“]”なら入力をポート1に転送して内部状態をポート2に出力する。内部状態が“)”なら入力を読み捨てる。 |
. . データの転送に比べて加算に多くの時間を要するプロセッサで構成されたシステムの場合には、第1列プロセッサがポート3の入力を内部状態に加算している間はそのポート3をビジーにし、第2列プロセッサがそのポート3の入力2つを加算して結果をポート2に出力する。第3列以降のプロセッサも同様に処理することにより上記動作規則5の第1列プロセッサの加算処理を並列処理することができる。
. . 演算子と演算子の積は後の演算子を列ベクトルに分解すれば演算子と各列ベクトルの積になるので、Fig. 2.4の超並列計算システムを列ベクトルの数だけ使用して並列計算することができる。その際、Fig. 2.4のシステムを層状に重ね、各プロセッサには入出力ポート4と5を設け、各層とその前後の層の同じ位置にあるプロセッサは入出力ポート4を前の層のプロセッサのポート5に接続し、入出力ポート5を後の層のプロセッサのポート4に接続することにより三次元構造に構成する。第一層のプロセッサはポート4を何処にも接続せず、必要ならそれにより自分が第一層にあることを認識してデータ処理をすることができる。説明の都合上プロセッサの位置を明記する場合には、P ijk と表し、iは層番号を、jは行番号を、kは列番号を表す。
. . 本計算システムに入力されるデータは(2.18)のベクトル Y が行列Yに変わるので(2.19)に示すように演算子“×”の後に行列Xと同じ形式の行列Yのデータが続く。第1層1行1列のプロセッサがこのデータを受けたとき、上に述べた[行列を読込む動作規則]により演算子“×”迄が処理され、第一層のプロセッサのスタックと内部状態にセットされる。この行列Xに行列Yの第1列を掛けるとき、第1列開始記号“(”の前に行列開始記号“[”が入力されること、及び、第1列終了記号の後に第2列開始記号が続くことにより、これらの処理のために上記の[行列にベクトルを掛ける動作規則]を少し変更した動作規則が必要である。
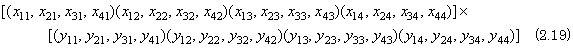
. . 第1層のプロセッサは行列開始記号“[”を一度だけ受取れるように転送し、これを受けたプロセッサはスタックにある行列Xの要素のコピーをポート5に出力する。この出力はポート4から第2層のプロセッサに読込まれ行列Yの第2列を掛けられる行列Xを構成する。P111は行列Yの第1列開始記号“(”を受け、第1層プロセッサは上記「行列にベクトルを掛ける動作規則」により行列Xに行列Yの第1列を掛ける計算を行う。但し、同規則第2項のスタックの“[”を捨てる動作は行わない。これは結果の行列を出力するとき必要になるからである。P111は行列の第1列終了記号“)”をポート3に転送した後第2列の開始記号“(”を受けるので、ポート5に“×”と“[”を出力した後“(”以降のポート0の入力をすべてポート5に転送する。第2層の先頭プロセッサP211はポート4の入力をポート0の入力とみなして処理し、第2層のプロセッサは第1層のプロセッサと同様にして行列Xと行列Yの第2列の積を計算する。第3層以降のプロセッサも同様にして行列Xと行列Yの第3列以降の各列との積を計算する。その結果2つの行列の積は各層の第1列プロセッサの内部状態で表される。このための各プロセッサの動作規則は次のようになる。
| . .[行列に行列を掛ける動作規則] | |
|---|---|
| 1. | 第1層のプロセッサは[行列を読込む動作規則]1から4により被演算行列を読込み、以下の動作規則へ移行する。 |
| 2. | ポート4を接続しているプロセッサは(=第2層以降)ポート4の入力を内部状態にセットし、次のポート4の入力が数値なら内部状態をスタックに積んで数値を内部状態にセットする。ポート4の入力が演算子“×”なら(=各層の第1行1列プロセッサ)以後ポート4の入力をポート0の入力とみなす。これを含めるとき、ポート0(ポート4)の入力と記述する。 |
| 3. | ポート0(ポート4)又はポート2の入力が演算記号“×”のとき、内部状態が数値ならスタックに積んで入力を内部状態にセットし、“×”がポート0(ポート4)の入力ならポート1と3に、ポート2の入力ならポート3にコピーを出力する。内部状態が数値でないならスタックに積まず、内部状態が“]”なら“×”を捨て、内部状態が“)”なら“×”をポート3へ転送する。 |
| 4. | ポート0(ポート4)又はポート2の入力が行列開始記号“[”のとき、内部状態が“×”ならスタックの“(”と数値、又は“,”と数値のコピーをポート5に出力し、“[”がポート0(ポート4)の入力ならポート1と3に転送し、ポート2の入力ならポート3に転送する。内部状態が“]”又は“)”ならそのコピーをポート5に出力し、内部状態が“)”なら入力“[”をポート3に転送する。 |
| 5. | ポート0(ポート4)の入力が“(”のとき、“)”を転送した後なら“×”と“[”をポート5に出力してから以後のポート0(ポート4)の入力をポート5に転送する。“)”を転送していないとき、内部状態が“×”なら入力を内部状態にセットし、“[”を転送していないならスタックの“[”を捨てる。 |
| 6. | ポート0(ポート2)(ポート4)の入力が“,”のとき、内部状態が“×”なら入力を読み捨てる。内部状態が数値なら入力をポート3に転送する。 |
| 7. | ポート0(ポート2)(ポート4)の入力が数値のとき、内部状態が“(”又は“×”なら入力を内部状態にセットし、コピーをポート1に出力する。内部状態が数値なら入力をポート3に転送する。内部状態が“)”なら入力を読み捨てる。 |
| 8. | 内部状態に数値をセットしたプロセッサはデータ転送と平行して内部状態にスタックの数値を掛ける計算を開始し、完了したらポート2に結果を出力し、スタックをクリアし、ポート3の入力をポート2に転送する。但し、ポート2を接続していない第1列プロセッサはポート3の入力を全て内部状態に加算し、ポート3の入力が“]”なら加算を終了する。 |
| 9. | ポート0(ポート4)又はポート2の入力が“)”のとき、内部状態が数値なら入力をポート3に転送する。内部状態が“]”なら入力をポート1に転送して内部状態をポート2に出力する。内部状態が“)”なら入力を読み捨てる。 |
| 10. | ポート0(ポート4)の入力が“]”のとき、“)”を受けたすぐ後なら入力をポート5に転送する。“×”を受けていないなら(=最終層)内部状態およびスタックをクリアし、ポート0(ポート4)の入力はポート1と3に転送し、ポート2の入力はポート3に転送する。但し、内部状態が“)”ならポート1へは転送せず、内部状態が“]”ならポート3へは転送しない。 |
. . (2.18)の積は(2.19)の行列Yの要素が第1列だけの場合であるから上記の行列と行列の積として処理することができる。その際、(2.18)のように行列Yの行列開始記号と終了記号は使用されないのが普通であるが、その場合にはポート4とポート5を使用する動作規則が実行されないのでデータが第2層に転送されることがなく、第1層のプロセッサで処理され前記の行列にベクトルを掛ける動作規則と同じ結果になる。
2.7 演算子の商の超並列処理
. .
ベクトルの商Y/XはY=AXの関係にある行列Aが商であるが、行列Aがベクトルの行列展開ではないときYとXから計算することはできない。行列Aの全要素を未知数とした連立1次方程式は解けないからである。ベクトルの表す関数y(t)とx(t)の商y(t)/x(t)が関数でなく微積分のような作要素であるとき、これをy(t)とx(t)から求めることはできないのと同じである。第3章で微積分演算子を導いたように、行列Aはy(t)が階差の数式で表されたx(t)の数式積分であることにより求めなければならない。
. .
一方、ベクトルXはベクトルYと行列Aの商であり、X=A−1Yと表せるからAの逆行列を求めれば演算子とベクトルの積の超並列処理で求めることができる。微分演算子と積分演算子はこのAとA−1の関係にあるから逆行列の計算は必要ない。又、一般の演算子Aの場合には、逆行列を求める代わりに、連立一次方程式の数値解法である消去法の計算を超並列処理で行うことができる。行列AとベクトルYの要素を一次元的に表記すればA−1Yは(2.20)で表すことができる。この計算は、逆行列記号“−1”と掛算記号“×”を合わせた物を消去法の演算を表すひとつの記号と考えれば2項演算であり、行列にベクトルを掛ける(2.18)の計算と同様にFig. 2.4の2次元配列プロセッサにより並列計算される。
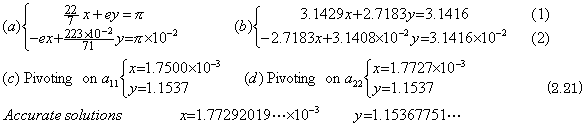
. . 第1行1列のプロセッサはベクトルYの要素終了記号“)”を転送した後、ポート3にピボットフラグを出力する。ポート2にこれを受けた第1行2列のプロセッサはピボット動作を行う。通常の行列要素の表記にあわせて、このピボットを第1行1列と表記するために、ベクトルYの要素を内部状態とする列を第0列と表記する。第1行1列のプロセッサはポート2と3にピボット行であることを示すフラグを出力、ポート1にピボット列であることを示すフラグを出力し、次に、内部状態a11をそれらのポートに出力して内部状態に1をセットする。その他の第1行のプロセッサはポート2に受けたピボット行フラグをポート3に転送し、内部状態のコピーをポート1に出力して内部状態をポート2の入力a11で除算すると共にa11をポート3に転送する、即ち、(2.22)(c)の計算を行う。但し、第0行プロセッサはポート3の入力a11を使用する。
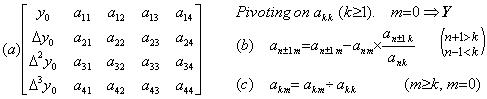 _____(2.22)
_____(2.22). . 第2行2列のプロセッサはポート2と3にピボット行フラグを出力し、第1行1列のプロセッサと異なりポート0を接続しているのでピボット列フラグをポート0と1に出力し、これら4ポートに内部状態を出力して内部状態に1をセットする。その他の第2行のプロセッサはピボット行にあったときの第1行のプロセッサと同じ動作に加えてポート0にも内部状態を出力する。但し、以前ピボット列にあった第1列のプロセッサはポート3の入力をポート2へ転送することのみ行う。第2行以外の第2列のプロセッサはピボット列にあったときの第1列プロセッサと同様に内部状態に0をセットし、その他のプロセッサは(2.22)(b)の計算をする。但し、第1行のプロセッサは減算にポート0でなくポート1の入力を使用する。第2行2列のプロセッサは内部状態に1をセットした後ピボットフラグをポート1に出力、第3行2列のプロセッサはこれをポート3に出力、ポート2にこれを受けて第3行3列のプロセッサがピボットとなる。
. . 以下同様にして最後の行と列がピボット行およびピボット列の動作を終えると計算が終了し、行列は単位行列になり、第0列に解が求まる。一般にn元連立1次方程式を解くにはn2に比例する計算時間を必要とするが、この超並列システムではnに比例する計算時間となり著しい並列化効果が得られる。この計算所要時間は次のように求められる。内部状態がy0である第1行0列のプロセッサはピボットが第1行1列のとき(2.22)(c)の計算を行い、以後、ピボットが第n行n列に達するまで(2.22)(b)の計算をn−1回行う。この計算時間には必要なデータが到達するまでの平均転送時間も含まれている。この超並列システムの全てのプロセッサが同じプログラムでこれらの計算を行うためには次のような動作規則が必要である。
| . .[連立1次方程式を読込む動作規則] | |
|---|---|
| 1. | 行列を読込む動作規則1から4により行列Aを読込み、消去法の演算記号“−1×”の入力により以下の規則へ移行する。 |
| 2. | ポート0の入力が“−1×”のとき、内部状態が数値なら入力をポート1と3に転送し、内部状態が“)”なら入力をポート3に転送する。 |
| 3. | ポート2の入力が“−1×”のとき、内部状態が数値又は“)”なら入力をポート3に転送し、内部状態が“]”なら読み捨てる。 |
| 4. | ポート0の入力がベクトル要素の開始記号“(”又は要素の区切り記号“,”のとき、内部状態が数値なら内部状態をポート3に出力して入力を内部状態にセットする。 |
| 5. | ポート0の入力が数値のとき、内部状態が“(”又は“,”ならポート3に出力して入力を内部状態にセットする。セットした後はポート0の入力をポート1に転送する。 |
| 6. | ポート0の入力が要素終了記号“)”のとき、内部状態が“)”なら入力をポート3に転送して消去法の動作規則へ移行する。内部状態が数値なら入力をポート1に転送して消去法の動作規則へ移行する。その際、規則5でベクトルの要素開始記号“(”をポート3に出力した第1行0列プロセッサはピボットフラグをポート3に出力する。 |
| 7. | ポート2の入力が数値なら内部状態をポート3に出力して入力を内部状態にセットし、ポート2の入力が“(”又は“,”又は“)”ならポート3に転送して消去法の動作規則へ移行する。 |
| . .[消去法の動作規則] | |
|---|---|
| 1. | ポート2の入力がピボットフラグなら、ポート2と3にピボット行フラグを出力、ポート0と1にピボット列フラグを出力し、これらのポートに内部状態を出力して内部状態に1をセットし、ポート1にピボットフラグを出力する。 |
| 2. | ポート2又は3の入力がピボット行フラグのとき、ポート2の入力ならポート3へ、ポート3の入力ならポート2へ転送し、ポート0と1に内部状態のコピーを出力する。続いて、ポート2又は3に受ける数値入力を同様に転送すると共にそれにより内部状態を除算する。 |
| 3. | ポート0又は1の入力がピボット列フラグのとき、ポート0の入力ならポート1へ、ポート1の入力ならポート0へ転送し、続いて内部状態のコピーを出力し、次のポート0又は1の数値入力により内部状態を除算した値をポート2と3に出力し、内部状態に0をセットする。 |
| 4. | ピボット列フラグを受けずに、ポート0に数値入力を受けたプロセッサはポート1へ、ポート1に数値入力を受けたプロセッサはポート0へ内部状態のコピーを出力し、内部状態をスタックに積み、入力を内部状態にセットする。次にポート2又は3の数値入力をポート2の入力ならポート3へ、ポート3の入力ならポート2へ転送すると共にその値を内部状態に掛けてスタックの値より減じて内部状態にセットする。 |
| 5. | 但し、以前ピボット列にあって内部状態に1又は0をセットしたプロセッサは以後、データの転送のみを行う。 |
| 6. | ポート0にピボットフラグを受けたとき、内部状態が数値なら入力をポート3に転送する。内部状態が“)”なら計算終了フラグをポート0に返す。 |
| 7. | ポート1に計算終了フラグを受けたらポート2にそれを転送し、ポート3に計算終了フラグを受けたらポート0に転送する。但し、第1行0列プロセッサはポート3に計算終了フラグを受けるがポート2を接続していないことによりポート0への転送は行わず、計算結果の出力要求“=”をポート0に受けて結果のベクトルの出力動作を行う。 |
| 8. | 接続していないポート(第1行のポート0、第0列のポート2) への出力は行わない。 |
. .
行列Aに対してY=AXの関係にあるベクトルYとXが複数組みあるとき、それらの関係は行列の積Y=AXで表せる。このとき行列Xは行列Yと行列Aの商、即ち、演算子の商である。|A|が零でないとき、行列Xの各列ベクトルは連立1次方程式の解X=A−1Yであるから、行列の商は、上に述べた連立1次方程式を解く超並列システムを層状に重ねた三次元配列プロセッサにより超並列計算することができる。本システムに入力されるデータは(2.23)で表され、行列Aと行列Yの任意の列ベクトルとの演算は上に述べた連立1次方程式の解法と同じであるが、行列Aの要素と行列Yの第2列以降のベクトルを第2層以降に転送することが必要である。この操作は行列の積(2.19)のときと同様に行列Yの開始記号“[”により行うことができる。
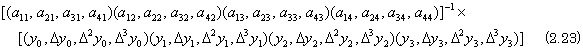
. . 連立1次方程式を読込む動作規則の1から3により行列A及び演算記号“−1×”迄が処理され、次に行列の開始記号“[”が入力され全てのプロセッサに転送され、それを受けたプロセッサは内部状態のコピーをポート5に出力、それをポート4に受けた第2層のプロセッサは内部状態にセットすることにより行列Aのコピーが第2層に構成される。第1層のプロセッサは行列Yの第1列ベクトルを同動作規則4以降により読込み、消去法の動作規則へ移行する。第1層の第1行0列プロセッサは行列Yの第1列の要素終了記号“)”を処理すると続いて第2列要素の開始記号“(”をポート0に受け、先ず、演算記号“−1×”と行列の開始記号“[”をポート5へ出力した後、“(”以降のポート0の入力をポート5に転送する。第2層の第1行0列のプロセッサは演算記号“−1×”以降のポート4の入力をポート0の入力とみなして第1層の第1行0列のプロセッサと同様に処理する。このポート0とみなすポート4を含めるときポート0(ポート4)と記述する。以下同様にして(2.23)の解が各層の第0列プロセッサの内部状態に得られる。このための動作規則は連立1次方程式を読込む動作規則に次の規則を加えればよい。
| . .[追加する動作規則] | |
|---|---|
| ♦ | ポート4の入力が数値なら内部状態にセットする。 |
| ♦ | ポート4の入力が演算記号“−1×”なら(=第2層以降の第1行0列プロセッサ)以後のポート4の入力をポート0の入力とみなす。 |
| ♦ | ポート0(ポート4)又はポート2の入力が行列開始記号“[”なら内部状態のコピーをポート5に出力し、入力がポート0(ポート4)からならポート1と3に転送し、入力がポート2からならポート3に転送する。 |
| ♦ | ポート0(ポート4)の入力がベクトル要素の開始記号“(”のとき、ベクトルの要素終了記号“)”を転送した後なら“−1×”と“[”をポート5に出力した後、“(”以降のポート0(ポート4)の入力をポート5に転送する。 |
. .
上に述べた演算子法の超並列処理(ポリプロセッシング)においてベクトルの要素が一つの場合、配列プロセッサは必要なく一つのプロセッサで処理され、その処理は通常の数値計算となる。又、演算子法の超並列処理システムがブラックボックスであり、その中の構造を見ることができず、入力したデータと出力された結果だけからその機能、構造を推定するとき、人間が紙に数式を書いて計算するのと同じ方法で、高性能な一つのコンピュータが高度なプログラムにより計算していると推定するのが最も簡単で容易に思いつく結論である。しかし、実際は超並列プロセッサが簡単な規則に基づく超並列処理(ポリプロセッシング)により計算している。著者が第一節で、目に見える世界と見えない世界では機能、構造は相似ではないと述べた意味である。著者の演算子法や連立1次方程式だけでなくあらゆる情報処理を超並列処理機構(ポリプロセッサ)により超並列処理(ポリプロセッシング)することができる。それらの代表的なものについては次節以降に述べる。
. .
著者は脳における情報処理もポリプロセッシングであると考える。脳細胞も身体の細胞も皆同じDNAを持っていて、身体の細胞は蛋白質を合成し細胞分裂するが、脳細胞は蛋白質の合成も細胞分裂も行わない。脳細胞は情報処理を行うためにDNAを使用していると考えられ、DNAはチューリングマシンのテープ、又は、マイクロコンピュータのROMに相当するものと考えられる。