4.4　微分解析と認識

　　図5.15の２分木はf₀, f₀′, f₀″, ・・・・・が未定のとき一般的なアナログ信号の形という概念、又は、関数という概念を表す。入力があると特定の関数を表し、f₀⁽³⁾以上が零なら２次関数、f₀″以上が零なら１次関数を表す。即ち、類という概念は根を基準にした部分木で表されるのであり、図5.15の２分木解析では分類という操作は行われていない。分類という概念は、n-1次関数はn次関数のtⁿの項の係数が零の特別な場合であり、n次関数に含まれるという関係を表現することである。従って、n次関数の分類木は図5.16の２分木で表される。これは図5.15の２分木からf₀⁽ⁿ⁾≠0に対応するn次関数という概念と、f₀⁽ⁿ⁾=0の部分木に対応するn-1次関数という概念を出力して２分木に表し、f₀^(n-1)≠0の関数とf₀^(n-1)=0の部分木に対応するn-2次関数に分けるという操作を繰り返して得られる。即ち、分類木は数式や言語と同じ外部表現である。
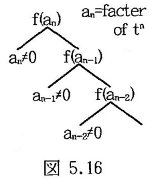　　図5.16の分類木でアナログ信号が分類木のどの位置に属すかを判定するには２分木を演繹的に辿ってf₀⁽ⁿ⁾, f₀^(n-1), ・・・・・, f₀′, f₀の順に零でないものを捜す必要があるが、これは微分操作と逆の手続きであり解析に時間を要する。又、この分類木は関数の次数という特徴だけに関するものであり、別の特徴に関しては別の分類木を必要とする。情報処理で分類木が用いられる理由は検索の範囲を絞り処理時間を短縮するためであるが、その処理時間の短縮はアナログ信号に含まれる無限の情報を分類の対象とした情報だけに限定することにより達成されている。当然に、可能な情報処理の範囲も限定されるのであり、知的情報処理におけるコンピュータの限界は分類という手法を用いることに起因すると言ってよい。
　　図5.15の２分木による解析は理想的状態ではt=0の瞬間に完了し、アナログ信号に含まれる全ての情報を抽出している。従って、その全ての情報の処理が可能である。アナログ信号が２次関数であれば、解析結果を(5.23)のn=2の数式で出力することができるが、これは２次関数であると答えたのと同じである。英語や日本語による出力でも、順序対(f₀, f₀′, f₀″)で出力しても同様である。又、順序対と言語の対応表により２次関数という言語で出力してもよい。これらの出力があればアナログ信号は認識されたのであり、従って、微分解析と認識は同じである。
　　微分解析はコンピュータによる文字の認識のような標準パターンとの比較解析ではなく、入力のアナログ信号だけで特徴抽出する点に特徴がある。標準パターンとの比較解析では比較事項に情報が限定され、又、予め記憶された標準パターンの範疇にない文字は処理できない。人間が著しく形の崩れた文字でも認識できるのは標準パターンを必要としない微分解析を行っているからである。
　　２次関数をy=at²+bt+cと表せばf₀″=2a, f₀′=b, f₀=cであるから、f₀′とf₀は２次関数の位置に関する情報であり、f₀″が２次関数の形に関する情報を示す。f₀″が大きければ頂点の尖った２次関数であり、小さければ頂点の曲率が小さく太い２次関数である。符号が負ならば180°回転した２次関数である。これらは文字が何処にあっても、大きくても小さくても、縦長でも横長でも上下が逆でも、人間が正しく認識できる原理を示している。２次関数であることは３次以上の微係数が零であることにより認識される。このとき、f₀⁽³⁾≠0を付け加えて出力すれば、t=0で互いに接し、この近傍で曲率の略等しい３次関数を答えたのであり、連想に相当する。
　　２次関数のアナログ信号の形が崩れている結果、f₀⁽³⁾が零でないが、著しく小さいとする。t=0の近傍ではf₀⁽³⁾の影響は殆どなく２次関数であるが、tが大になるとf₀⁽³⁾の影響により２次関数から外れる。従って、t=0の近傍を何の範囲と決めるかにより２次関数であるとも、３次関数であるとも答えることができる。これは曖昧と言われる現象であるが、普通は設問においてt=0の近傍を規定せず、認識側の自由に任せることに原因があり、設問が曖昧なのであって認識が曖昧なのではない。
　　文字パターンの形崩れはこれと同様にtが大なる点における情報であり、その文字の認識に重要でなく、型崩れがあっても文字の認識ができるためにはt=0の近傍の情報が重要なのである。周波数解析ならω=0の近傍は無意味でω→∞の領域が重要であるが、２次関数の周波数スペクトルはω³に逆比例するので重要な領域が減衰してしまう。文字パターンでも同様でスペクトル解析等の積分解析では重要な情報が失われてしまい、重要でない情報が強調されるのでパターンの形崩れを文字の違いと認識することになる。数式による理論計算では如何に減衰が大きくても正確な計算ができるから積分解析により認識を論ずることもできるが、数値計算やアナログ計算では脳並みの認識は期待できない。t=0の近傍、即ち、ωの大なる領域を強調するには微分解析でなければならない。
　　任意のアナログ信号を微分解析した結果は上記のように微係数のまゝで処理する他に、第４章3.2節(HPの4.2節)の微分方程式の導出及び同章3.3節(HPの4.3節)の周波数解析で述べた方法により周波数に変換することができる。２次関数の場合の微分方程式は定数関数y″=f₀″であるから周波数スペクトルは1/ωで２次関数のω²倍であり、微分解析による周波数解析は人間の感覚と同じである。音声の周波数解析は母子音という概念を生じ、光信号の周波数解析は色という概念を生ずる。これらの概念による情報処理も２分木で処理できる。
　　一般的な概念における認識は微分解析に相当する差分解析または違の検出による解析でなければならない。違いが見出されたとき新たな概念の認識が起こるから、環境の変化により認識能力は向上する。分類とは類似のものを集める処理であり、標本にないものは処理できない。従来、コンピュータによる認識では設計時に考慮された範囲を越えた認識処理はできない理由である。
　　赤い林檎と緑の林檎があるとき、両者に共通する情報は林檎であり、異なる情報は赤色と緑色である。従って、林檎をA、赤色をR、緑色をGで表して両者に共通するAを根のプロセッサの内部状態とし、異なるRとGをポート1とポート2に接続するプロセッサに転送すれば図5.17(a)の２分木が構成され、赤い林檎と緑の林檎が記憶される。赤い林檎を見せたとき、各プロセッサは内部状態と一致する情報を取り込んでそれをポート0に返すと、この２分木は記号の順序対(A, R)を出力する。これは赤い林稿を認識したという答である。黄色の林檎を見せれば(A, R, G)と答え、今迄見たことのない黄色の林檎を認識できる。これは思考と言われる現象である。赤い林檎を見せたとき、RをGに替えて(A, G)と答えれば緑の林檎の連想である。
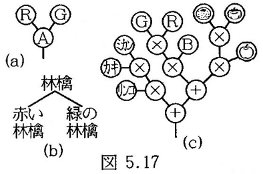　　分類という処理では、赤い林檎も緑の林檎も林檎という範疇に属すから図5.17(b)の２分木が構成される。この分類木を学習により構成することはできるが、この分類木により今迄見たことのない黄色の林檎を認識することはできない。黄色の林檎を分類木に記録した後でなければその認識はできないのである。
　　色は青赤緑の様々な割合の組み合わせで表され、色を持つ個体も林檎、柿、密柑等々あり、これらの関係を多分木で表すのは進歩はあっても進化がない。赤い林檎と緑の林檎の間には林檎という共通の情報があるが、赤色と林檎は異なる概念であり類似な点もないから２つの枝に分けなければならない。このとき、節のプロセッサの内部状態として演算子という概念が導入される。解析で林檎と赤色を分離したのであるから演算子は分離の逆操作で色を着ける操作である。この演算子は色が何であっても、個体が柿でも蜜柑でも、個体と色の間にある共通の情報である。
　　青赤緑は三原色であるから共通な点はないので２つの枝に分けなければならない。このとき、節のプロセッサには両者の混合操作を表す演算子が三原色の間にある共通の情報として導入される。着色より先に色の混合をしなければならないから演算子に操作の優先順位という概念が生ずる。従って、着色演算子を+で表し、混合演算子を×で表せば図5.17(c)の2分木で個体と色の関係を表すことができる。
　　この２分木解析では三原色を学習すれば七色を認識することができる。各色と濃度という概念を組にすれば無限の色を認識できる。林檎、柿、蜜柑という個体も演算子×で結合される。実際にこれらが混合された情報が入力されることはないが、林檎と柿を混合した中間体を認識したと答えることはできる。これは空想と言われる。
　　林檎や柿という個体には大きさや形状という情報もあり、これらもそれぞれ部分木を構成して演算子により一本の２分木に結合された構造となる。これは脳の機能分化と言われる現象に相当する。分類という処理では階層構造が用いられるが、これは外部表現の構造であり、脳の機能分化はこれとは点対象的な構造、即ち、ポリプロセッサと同じ２分木構造でなければならない。演算式の各項の記述順は計算の順序で規定されるが、個体名、色、形には決まった順序はない。しかし、この順序は学習又は設計により決定され、図5.17(c)の場合は個体名、色、形の順でなければならない。
　　個体名や形は色とは異なり、普通は、どれか一つの名前及び形を採るので演算子×は必ずしも必要ではない。このとき変数という概念が導入され、具体的な名前や形は変数に与えられる値となり、変数を内部状態とするプロセッサの局所RAMに記憶することができる。こゝに、２分木データベースという概念が生まれる。
　　所謂データベースシステムは主記憶装置にデータベースを構築し、管理プログラムが検索や更新を行う。この関係は数値計算プログラムとインタプリタまたはデコーダの関係に相当し、両者は明確に区別される。２分木データベースでは両者は一体であり、管理プログラムの機能を持つ２分木ポリプロセッサの各局所RAMに項目毎に分散されてデータベースが構築される。