4.3 視聴覚情報の超並列処理
自動制御で扱う入出力はLaplace変換の定義域の関数でt<0では関数値は零でなければならない。システムに入力が加わった瞬間がt=0であるからそれで差し支えないが、視聴覚情報は常に入力されていて、その一部を解析する場合に開始時刻をt=0としてよいけれども、t<0では零でt=0で突然初期値 f0の関数が入力開始すると考えることはできない。両者は微分演算子を掛けたとき結果に大きな相違が生ずる。Laplace変換の扱う関数及び導関数はユニットステップ関数を用いて、f(t)u(t), f ′(t)u(t),
f″(t)u(t), ・・・・・と表される。これらのLaplace変換をF(s), F′(s), F″(s), ・・・・・で表してこれらの関係を求める。u(0)=0, t>0のときu(t)=1であるから、
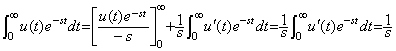 (5.4)
(5.4)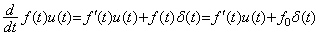 (5.5)
(5.5)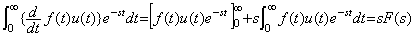 (5.6)
(5.6)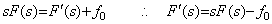 (5.7)
(5.7)故に、f0≠0であってもf(t)u(t)を微分することはLaplace変換ではF(s)に s を掛けることであり、結果にはf0δ(t)のインパルスが重畳する。積分定数を零としてこれを積分すると、
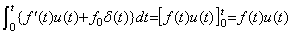 (5.8)
(5.8)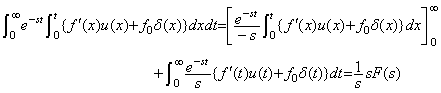 (5.9)
(5.9)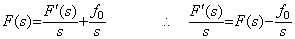 (5.10)
(5.10)故に、積分定数を零として積分することはLaplace変換では1/sを掛けることであり、 結果はf(t)の初期値 f0を回復する。即ち、Laplace変換はu′(t)=δ(t)となるu(t)を導入して関数をf(t)u(t),
f ′(t)u(t), ・・・・・に変換したことにより、微分演算が初期値をインパルスに変換するから微積分演算が可逆となる。
t≥0でf(t)である関数はLaplace変換可能ではあるが、u(t)を掛けてないので微分演算が初期値を変換しない。従って、それを積分定数零で積分すると初期値 f0が得られないのでf(t)-f0となる。この関係は上記の各式でu(t)を定数1に置き換えれば得られる。(5.4)でu(t)を1に置き換えると部分積分は必要なく、1/sが得られる。同様 に、関数f(t), f ′(t), f″(t), ・・・・・のLaplace変換はf(t)u(t), f ′(t)u(t), ・・・・・のそれと同じで、F(s), F′(s), F″(s), ・・・・・となる。(5.5)の右辺は単にf ′(t)となり、(5.6)の部分積分は第1項が零でないから(5.7)の右の式が直接得られる。即ち、微分することは s を掛けて初期値を引くことであり、(d/dt)f(t)=(d/dt){f(t)-f0}という普通の微分と同じである。(5.8)のf ′(t)の積分はf(t)-f0となり、(5.9)は、
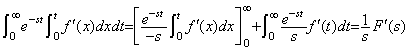 (5.11)
(5.11)unit doublet u″(t)=δ′(t)を導入すると(5.5)より、
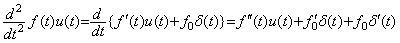 (5.12)
(5.12) (5.13)
(5.13)(5.5)により、f(t)u(t)を微分してインパルスf0δ(t)を抽出し、残りを再度微分すればインパルスf0′δ(t)を抽出できる。このようにしてf0, f0′, f0″, ・・・・・を抽出することができる。
 しかし、脳は1本のインパルスに乗った情報を認識する機能は持たず、インパルスは電波の搬送波に相当するものである。実際に、頭を急に振って別の場所に視野を移し、そこに書かれた文字を認識するには少し時間が必要であり、これは過渡応答の影響が消える迄正確な認識ができないことを示す。また、映画やテレビの画面に別の画面を毎秒1コマ程度混合しても認識できない。
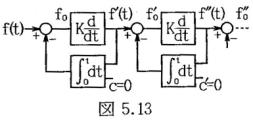
しかし、脳は1本のインパルスに乗った情報を認識する機能は持たず、インパルスは電波の搬送波に相当するものである。実際に、頭を急に振って別の場所に視野を移し、そこに書かれた文字を認識するには少し時間が必要であり、これは過渡応答の影響が消える迄正確な認識ができないことを示す。また、映画やテレビの画面に別の画面を毎秒1コマ程度混合しても認識できない。図5.13に示すように、微分増幅器に積分負帰還回路を設けた微分装置を従属接続して脳の解析装置を模擬する。1段目の入力をf(t)、出力をy(t)とすると、
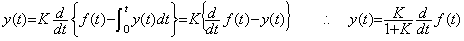 (5.14)
(5.14)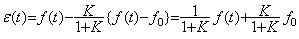
t=τで急に入力を零にすると、-f(t)u(t-τ)が入力に重ねられるから、
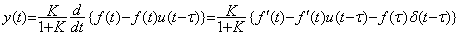
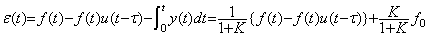
1段目の入力がf(t)u(t)であるとき、y(t)は(5.5)のk/(1+k)倍、その積分は(5.8)のK/(1+K)倍であるから、ε(t)は次式となりオフセットにf0は得られない。同様に、f0′, f0″, ・・・・・も得られず認識に必要な情報が得られない。
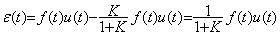
f(z+τ)u(z+τ)=f(z+τ)で、出力は(5.5)より、
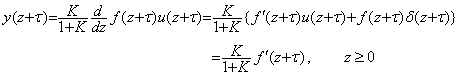
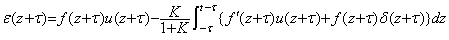
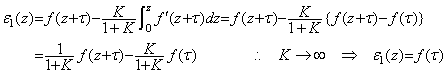
実現可能な簡単な微分及び積分回路は(5.15)の伝達関数で表され、f(t)に含まれる 最高周波数で決まるTL=1/ωHよりT1が十分に小で、最低周波数で決まるTH=1/ωLよりT2が十分に大であれば s 及び1/sと見做すことができ、上記の現象が生ずる。
 (5.15)
(5.15)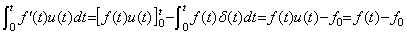
理想的な微分、積分回路又は数値微積分により図5.13を実現する場合には定数値のオフセットは微分出力に影響しないから自動制御の特性に影響はないが、入力が飽和するか、(5.15)の時定数T1, T2が条件を十分に満たさない場合は問題が生ずる。負帰還出力をg(t)、微分出力をy(t)とすれば、
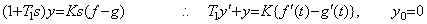 (5.16) (5.16) | ||
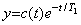 | と置けば、 |
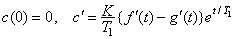 |
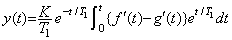 (5.17)
(5.17)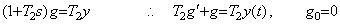 (5.18)
(5.18)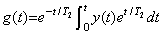 (5.19)
(5.19)f(t)とg(t)の関係は(5.16)と(5.18)からy, y′を消去すれば得られる。y0=0, g0=0であるからg0′=0であり、
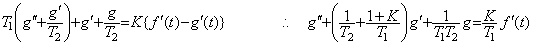
f ′(t)u(t)+f0δ(t)に置き換えれば2つの微分方程式に分けることができ、f0のg(t)への影響は次の微分方程式で得られる。
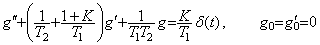 (5.20)
(5.20)u′(t)に替えてT1→0とした解が同じであるから、(5.21)によりδ(t)が定義される。t<0の場合をt=0に対称なδ(-t)で表せば、Diracのデルタ関数は{δ(-t)+δ(t)}/2に相当し、δ(t)は指数関数の極限関数であるからt≠0で無限に微分可能な連続関数であるが、t=0で不連続である。Diracのデルタ関数の積分値のみが必要な場合は差し支えないが、積分した関数はユニットステップ関数にならない。又、このδ(t)もδ0=∞であるからδ′, δ″, ・・・・・を定義できない。これが可能なδ(t)は本webページの第2章3.2節で定義したδ0, δ0′, δ0″, ・・・・・が全て零のインパルス関数である。
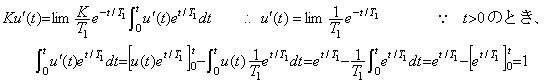
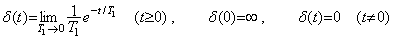 (5.21)
(5.21)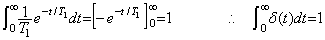
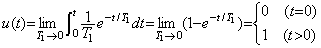 (5.22)
(5.22)インパルス応答(5.20)はδ(t)を(5.21)の指数関数に置き換えて解いた後にT1→0として得られる。その結果は、(5.20)に初期値を代入してg″ を微小区間積分したg0′ を初期値とする、g0=0, g0′=Kf0/T1の同次方程式と同じである。故に、その解は、
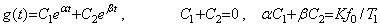
T1«T2なら、
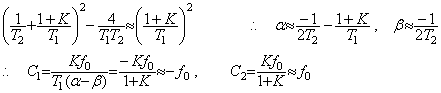
g(t)は図5.14(a)の太線で表され、オフセットf0u(t)-g(t)は同図(b)の太線で表される。従って、t>2T2ならば0.63f0以上のオフセットが得られる。(5.15)の1次遅れ伝達関数の入出力関係は(5.19)で表され、[0, t]の積分結果に時定数T2の減衰関数が掛けられているからt=T2において0.37f0にリセットしたことに相当し、t=2T2で0.63f0のオフセットが得られるのである。
このオフセットは定数でないから(5.17)により出力に影響を及ぼし、応答特性改善のため微分制御を付加したシステムでは不測の事態を招く。工程制御では制御装置をOFFにすれば工程も停止するから差し支えないが、飛行機はオートパイロットをOFFにしても飛び続けなければならない。水平飛行のときはオートパイロットをON-OFFしても何の影響もないが、着陸体制でこの操作を行えば制御不能に陥る。
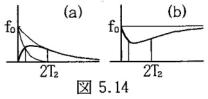 白紙の左半分を黒く塗りつぶし、境界線に垂直な線を t 軸とすれば、t 軸上の明暗はf0u(t)で表すことができる。このとき、図5.14(b)のオフセットはマッハ帯と呼ばれる現象である。この場合は、t<0の方向の明暗の変化にもt>0の場合と点対称的なマッハ帯が観測される。マッハ帯は図5.13の微分増幅器と積分負帰還回路が理想的な微分と積分でないことに起因して、明暗の変化速度が時定数T1の減衰速度より速い場合に起こり、変化が遅い場合には起きない。
白紙の左半分を黒く塗りつぶし、境界線に垂直な線を t 軸とすれば、t 軸上の明暗はf0u(t)で表すことができる。このとき、図5.14(b)のオフセットはマッハ帯と呼ばれる現象である。この場合は、t<0の方向の明暗の変化にもt>0の場合と点対称的なマッハ帯が観測される。マッハ帯は図5.13の微分増幅器と積分負帰還回路が理想的な微分と積分でないことに起因して、明暗の変化速度が時定数T1の減衰速度より速い場合に起こり、変化が遅い場合には起きない。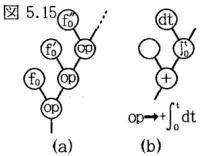 図5.13の回路に、視聴覚に起こるこれらの現象が起こることは、脳がこのような回路で微分解析を行っていることを示す。各段の負帰還微分増幅器の機能を1つのプロセッサで実現し、オフセットをポート1に接続するプロセッサに転送すればf(t)の2分木解析ポリプロセッサが実現される。f0, f0′, f0″, ・・・・・が確定すればTaylor展開によりf(t)が確定するから、この解析により
図5.13の回路に、視聴覚に起こるこれらの現象が起こることは、脳がこのような回路で微分解析を行っていることを示す。各段の負帰還微分増幅器の機能を1つのプロセッサで実現し、オフセットをポート1に接続するプロセッサに転送すればf(t)の2分木解析ポリプロセッサが実現される。f0, f0′, f0″, ・・・・・が確定すればTaylor展開によりf(t)が確定するから、この解析によりf(t)の特徴の抽出は完全である。2分木の節のプロセッサの微分機能は演算式の解析動作規則に相当し、演算子に相当する内部状態は積分作用でなければならない。従って、図5.15(a)の2分木によりf(t)の解析結果を表すことができ、更に、+, ∫, dtを分離して詳細に表せば同図(b)の2分木でopを内部状態とするプロセッサを置き換えることができる。
図(a)の演算子を内部状態とするプロセッサがポート1と2の入力に演算を行いポート0に出力するとf(t)が再生される。このとき、f(t)は次式で表される。
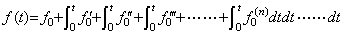 (5.23)
(5.23)| f(t) is f0 plus the integral of the function which is f0′ plus the integral of the function which is f0″ plus the integral of ・・・・・ |
| 「f0(n)を積分してf0(n-1)を加え、積分してf0(n-2)を加え、・・・・・、積分してf0″ を加え、積分してf0′ を加え、積分してf0を加えればf(t)」 |