第四章 . .微分方程式及び応用
1. 一階の微分方程式
1.1 本演算子法による解法
. .
一階の微分方程式は一般に次のように表すことができる。f(y)は微分方程式を駆動する関数に依存するがその関数の明記は省略する。
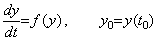 ________(1.1)
________(1.1)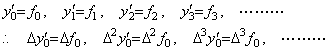
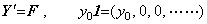 ______(1.2)
______(1.2)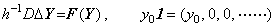 ______(1.3)
______(1.3)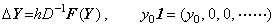 ______(1.4)
______(1.4)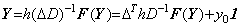 ______(1.5)
______(1.5). . 右辺の関数 f が解 y(t)に依存するとき、(1.4) の積分演算は任意の Y 及び Z に対して次の関係になる。
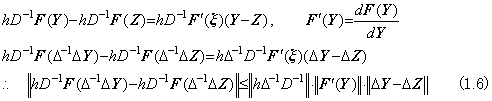
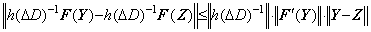 ______(1.7)
______(1.7)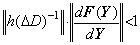 ________(1.8)
________(1.8)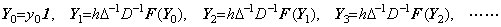
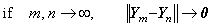 ________(1.9)
________(1.9). . 初期値 y0 が零であり、f( y0 )の値も零であり、且つ、関数 f(y)が y(t)以外に変数 t を持たないなら、この反復は恒等的に零の解を与える。もし、恒等的に零でない解が存在するなら、最初の反復処理はその解を得るために幾分変えなければならない。上記の条件の一つが満たされなければ恒等的には零でない解が得られる。
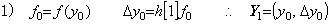
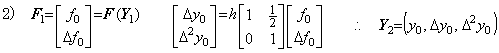
Δy0 は修正され、 Δ2y0 が予測される。
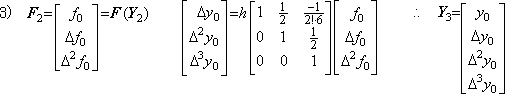
Δy0 及び Δ2y0 は修正され、 Δ3y0 が予測される。
4)__同様にして、予測を伴った修正を Yn−1 が得られるまで反復する。但し、n の値は予め指定される。
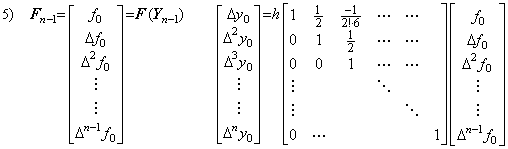
Δy0, Δ2y0, ………, Δn−1y0 が修正され、Δny0 が予測される。故に、
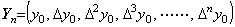
6)__Yn の全ての要素が(n×(n+1))次の矩形行列の積分演算子により修正される。
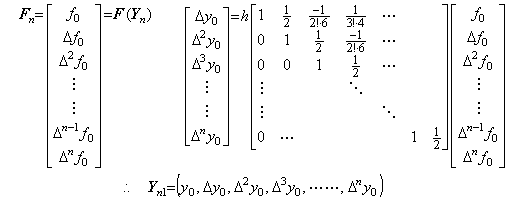 ___(1.10)
___(1.10). . Yn1−Yn のノルムが解の最後の有効桁の最小値より大きい値 ε より小さいなら、Yn1 は収束解である。その条件が満たされないならもう一度(1.10)で表された修正を Yn の代わりに Yn1 を用いて繰り返す必要がある。その結果を Yn2 で表すと、Yn2−Yn1 のノルムが ε より小さいなら Yn2 は収束解である。その条件が満たされないなら未だ収束でない。この場合、n の値を増加するか、条件(1.8)が十分に満たされていないかそのチェックがされていないなら等間隔区分幅 h を減少する必要がある。計算所要時間を短縮するためには等間隔区分幅を半分にするのが良い。
. . n=2 及び n=4 の場合は、著者はベクトル計算を使わずに上記のベクトル式を等間隔点の関数値 yk と fk を使う式に変換したプログラムを示した。しかし、n の値が 3 より大きいときはベクトル計算を使う方が良い。何故なら、積分行列の第一行と被演算ベクトルの積を計算するサブルーチンを他の行と被演算ベクトルの積全てを計算するために使うことができるからである。これはプログラムを簡単にし、並列計算を容易にする。
1.2 数式処理による解
. .
等間隔区分幅を記号 h で表すと、ベクトルの要素は記号 h を用いて表される。要素が記号で表された(1.10)の積分行列を使うと、数式処理により数式で表された解を得ることができる。その解は剰余項つきの Taylor 展開であるが剰余項は誤差を持つ。
. .
微分方程式 y' =−ty, y(0)=1 は次のような剰余項つき Taylor 展開で表される解を持つ。
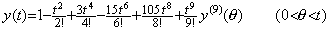 ______(1.11)
______(1.11)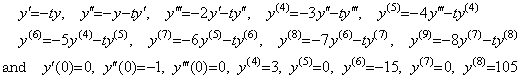
. . ベクトル関数を用いると、この微分方程式は次のように表される。
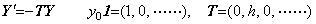 _____(1.12)
_____(1.12)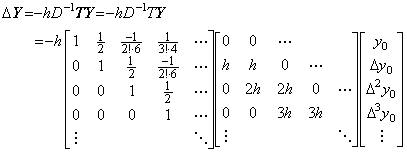 ____(1.13)
____(1.13)1)__

______誤差は剰余項 y' (ξ)h である。
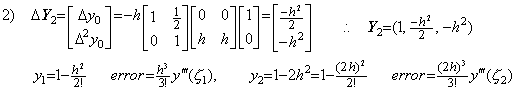
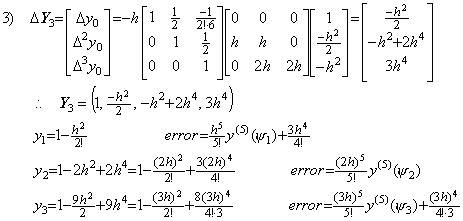
4)__3行4列の積分演算子を用いて Y3 を修正すると、
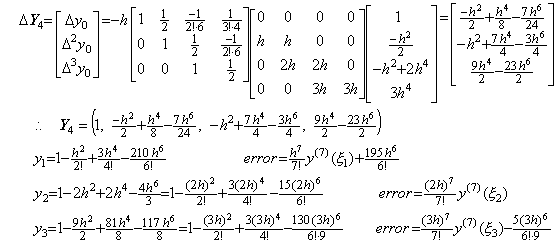
5)__もう一度3行4列の積分演算子を用いて Y4 を修正すると、
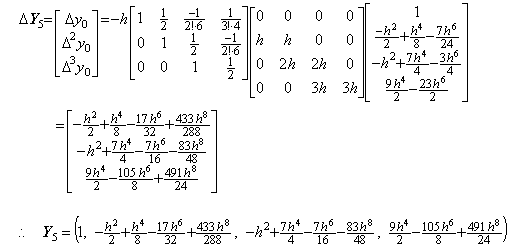
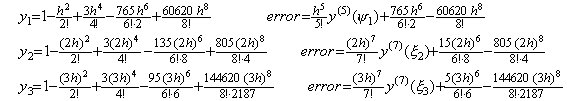
. . 数式で表した解はこの二度の修正で得られた結果の一致した部分である。3行4列の積分行列を用いる二度より多くの修正は h6 の項の正しい係数を得られず、非常に大きな係数を持つ h8, h9, ……… 等の項を生ずる。Taylor 展開が収束するための条件を区間 3h が十分に満たさないなら、これ等の項は異常な解の原因となる。しかし、実際の数値解では Taylor 展開に一致しない高次の項がすべて誤差ではないことに注意しなければならない。数値解が正しい値であるためには、Taylor 展開に一致する h4 迄の項の他に剰余項が必要である。Taylor 展開に一致しない高次の項はその剰余項の一部でもあり、必ずしも数値解の誤差ではないのである。その実例は第1.4節の外挿解法の実例で示す。
. . Taylor 展開(1.11)の t=0, h, 2h, 3h における y(t)の逐次階差を計算すると下記に示す結果が得られ、上記のベクトルで表された解の各要素をこれと比較すると、h4 の項以降が一致しない。しかし、ステップ 4)とステップ 5)の h4 の項は一致しており、収束している。更に、この項迄を使用した解 y1, y2, y3 は h4 の項迄 Taylor 展開(1.11)に一致している。これは、ベクトル要素の h4 の項は Taylor 展開に一致しなくても収束していれば良いことになる。従って、ベクトルを関数に変換しなくても、ベクトルの要素により下記の収束判定を行うことができる。数値計算の場合も同様である。
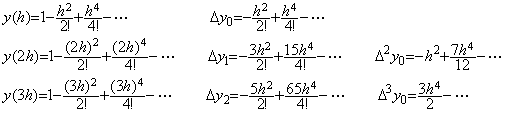
. . 数値計算においては、ステップ3), 4), 5)の結果は数値解が収束しているか否かを決定できるデータを与える。ステップ3)と4)の結果に有意な違いがなければ h4 の項の係数の違いは有意ではなく、解は収束している。それらの間にいくらかの有意の違いがあるなら h4 の項の係数の違いは有意である。この場合、ステップ4)と5)の結果に有意な違いがないなら h6 の項の係数の違いは有意ではなく、解は収束している。それらの間にいくらかの有意な違いがあるなら h6 の項の係数の違いは有意であり、解は未だ収束ではない。この場合、区間 4h が Taylor 展開の要求する条件を十分に満たしているなら n の値を 1 増加してよい。区間 4h がその条件を十分に満たしていないなら等間隔区分幅 h を減じなければならない。これらが、著者の演算子法が前節で述べた処理手続きを用いる理由である。
. . 等間隔区分幅を減じたなら反復法はステップ1)から再出発しなければならない。n の値を増加したならステップ1)から再出発するか、ステップ4)から積分行列 D−1の第4行を追加して継続しなければならない。ステップ5)の結果を使用してはならない。何故なら、それは係数の正しくない h6 及び h8 の項を持っているからである。従って、n=4 の場合にはステップ4)以降は次のように部分修正される。
4)__積分行列の第4行を追加すると、次のように Δ4y0 が ΔY4 に追加される。
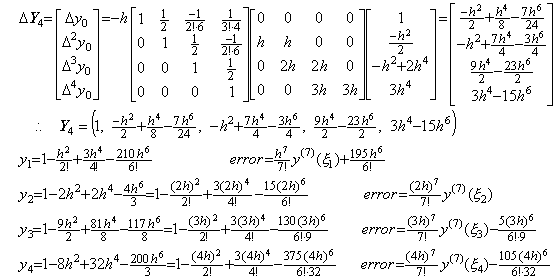
5)__4行5列の積分行列を用いて Y4 を修正すると、
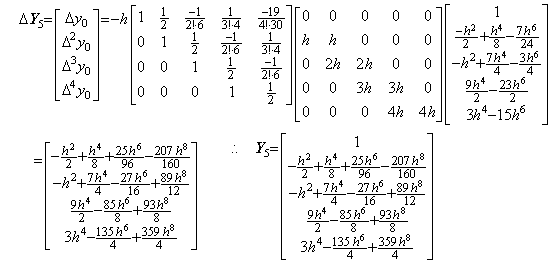
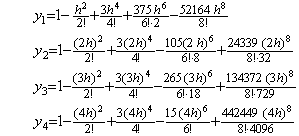
6)__もう一度4行5列の積分行列を用いて Y5 を修正すると、

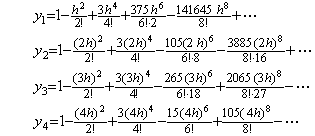
. . 4行4列の積分行列を用いた予測ステップ4)は y2 だけが h6 迄正しい項を持つ結果を与える。しかし、4行5列の積分行列を用いた修正ステップ5)は y4 だけが h6 迄正しい項を持つ結果を与える。4行5列の積分行列を用いてもう一度修正するステップ6)は h6 迄の全ての項が収束である結果を与える。しかし、y4 が h6 及び h8 の正しい項を持つのを除いて h6 の項の係数は正しくない。全て正しい h6 の項を得るためには、5行5列の積分行列を用いて予測ステップ5)を行い、5行6列の積分行列を用いて二度の修正ステップを行わなければならない。
. . これらが、第二章のプログラムで n 行 n+1 列の積分行列を用いた場合にノルムの代わりに yn の収束により数値解の収束を判定し、又、 yn を初期値として次の n 区間を解いていく理由である。従来のP-C法のように1区間づつ進行する方法は解の精度と安定性に多少の損失を生ずる。
. . Milne の予測子は上記ステップ4)における y4 の計算と同じものであるが、その h6 の項は正しくない。彼の修正子は Simpson の1/3則であり精度は予測子より悪いから、その項を正しくすることは出来ない。彼の予測子は前節のステップ5)で4行4列の積分行列を用いて次のように求められる。
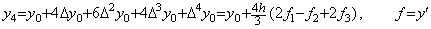 _____(1.14)
_____(1.14)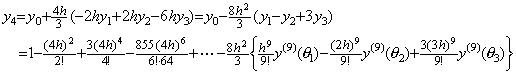 ___(1.15)
___(1.15). . 微分方程式により与えられる値を Milne の修正子に代入し、(1.11)で表される二つの正確な値 y2, y3 及び、予測値 y4 の h6 の項以外の誤差を ER で表したものを与えると、
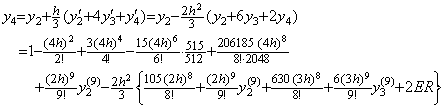 ____(1.16)
____(1.16). . 通常、Milne 法は y0, y1, y2, y3 の結果を用いて t3=t0+3h から t4=t0+4h 迄の区間 h を積分すると見なされている。しかし、(1.15)及び(1.16)に示したように t0 から t4 迄の4区間の積分である。その級数が収束するためには、Taylor 展開が収束する条件をその4区間 4h が十分に満たすことが必要である。一方、Runge-K 法は以下に示すように区間 h をその半分の区間を用いて積分し、区間 h がその条件を十分に満たすことを必要とするのみである。
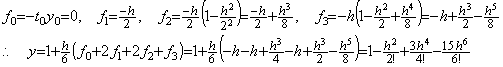
. . 表1.1は初期値 y(0)=10 に対する数値計算結果の比較を示す。Milne 1 の欄は修正子を一度だけ使用する Milne 法の結果を示す。Milne 2 の欄は修正子を N 回以上使用する結果を示す。N の値は大括弧の中に示され、解の収束を表す。但し、N=21 は収束しないことを示す。前者は t=5 より後では後者よりずっと正確で安定である。修正子の繰返し使用は t=5 より後の悪い結果をもたらすだけで殆ど効果はない。
. . R.-K. 1 の欄は Milne の予測子の積分区間である4区間を積分する Runge-K.法の結果を示す。この結果は Milne 1 より少し悪く、t=4 の後は意味がない。R.-K. 2 の欄は Milne の修正子の積分区間である2区間を積分する Runge-K.法の結果を示す。この結果は t=0 の辺りでは Milne 1 よりやや良いが、t=1.6 より後では Milne 1 より悪くなる。R.-K. 3 の欄はこの二つの解法の従来の比較で使用される積分区間である1区間を積分する Runge-K.法の結果を示す。この結果は Milne 1 より良いが、この比較は積分範囲が Milne 法の修正子の半分であるから意味がない。
| 表 1.1 Milne法とRunge-Kutta法の比較 | |||||||
|---|---|---|---|---|---|---|---|
| t | Milne 1 | [N] Milne 2 | 真 値 | 10n | R.-K. 1 | R.-K. 2 | R.-K.3 |
| -0.2 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6.0 |
* * * * 9.801985 9.559971 9.231156 8.824958 8.352687 7.827025 7.261467 6.669740 6.065277 5.460712 4.867491 4.295543 3.753084 3.246501 2.780355 2.357447 1.978980 1.644742 1.353355 1.102511 8.892256 7.100641 5.613601 4.393810 3.404867 2.612241 1.984204 1.492146 1.110959 8.189017 5.976289 4.317867 3.088738 2.187330 1.533693 1.064518 7.316307 4.976955 3.352948 2.235188 1.476127 9.641744 6.242481 3.994103 2.535664 1.588600 9.891442 6.065259 3.704269 2.222832 1.330509 7.824053 4.573649 2.649826 1.498494 8.658934 4.659715 2.722967 1.388222 |
* * * * [1] 9.801985 [2] 9.559971 [2] 9.231157 [2] 8.824961 [2] 8.352690 [2] 7.827032 [2] 7.261475 [2] 6.669752 [2] 6.065289 [2] 5.460727 [21] 4.867506 [2] 4.295559 [2] 3.753097 [3] 3.246514 [2] 2.780364 [3] 2.357455 [3] 1.978982 [3] 1.644743 [3] 1.353352 [3] 1.102507 [4] 8.892171 [4] 7.100566 [3] 5.613492 [4] 4.393728 [3] 3.404758 [3] 2.612172 [4] 1.984113 [3] 1.492105 [3] 1.110893 [4] 8.188920 [21] 5.975855 [5] 4.318048 [5] 3.088463 [21] 2.187724 [5] 1.533482 [5] 1.065061 [5] 7.313908 [21] 4.983469 [4] 3.349478 [7] 2.242724 [6] 1.470929 [8] 9.730303 [7] 6.166814 [8] 4.102402 [8] 2.428532 [9] 1.726982 [8] 8.395819 [9] 7.900475 [9] 1.620723 [10] 4.726138 [10]-1.587930 [11] 4.269(-5) [21]-3.669(-5) [11] 5.203(-5) [11]-5.751(-5) [11] 7.179(-5) [11]-8.492(-5) [12] 1.035(-4) [21]-1.249(-4) |
9.80198673 9.95012479 1.00000000 9.95012479 9.80198673 9.55997478 9.23116344 8.82496903 8.35270199 7.82704545 7.26149030 6.66976789 6.06530660 5.46074412 4.86752228 4.29557318 3.75311111 3.24652467 2.78037290 2.35746057 1.97898674 1.64474464 1.35335283 1.10250492 8.89216081 7.10053615 5.61347500 4.39369336 3.40474421 2.61214065 1.98410974 1.49207819 1.11089965 8.18869738 5.97602198 4.31784069 3.08871441 2.18749112 1.53380989 1.06476605 7.31802551 4.97955236 3.35462628 2.23745881 1.47748183 9.65933345 6.25214775 4.00652974 2.54193577 1.59667624 9.92949522 6.11356511 3.72665317 2.24905706 1.34381028 7.94938558 4.65571332 2.69957850 1.54975396 8.80816483 4.95639984 2.76124090 1.52299797 |
+0 +0 +1 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -2 -2 -2 -2 -2 -2 -2 -3 -3 -3 -3 -3 -4 -4 -4 -4 -4 -5 -5 -5 -5 -5 -6 -6 -6 -6 -7 -7 -7 -7 |
* * * * * * 9.231147 * * * 7.261394 * * * 4.867729 * * * 2.782125 * * * 1.357819 * * * 5.681144 * * * 2.055314 * * * 6.536229 * * * 1.879862 * * * 5.107530 * * * 1.390(-3) * * * 4.047(-4) * * * 1.345(-4) * * * 5.365(-5) * * * 2.659(-5) |
* * * * 9.801987 * 9.231163 * 8.352701 * 7.261490 * 6.065314 * 4.867548 * 3.753172 * 2.780485 * 1.979161 * 1.353590 * 8.895055 * 5.616689 * 3.408020 * 1.987196 * 1.113606 * 5.998208 * 3.105769 * 1.546143 * 7.402126 * 3.408833 * 1.510565 * 6.443620 * 2.647193 * 1.047986 * 4.000694 * 1.473920 * 5.245412 * 1.805212 * 6.015464 * 1.943720 |
* * * 9.950125 9.801987 9.559975 9.231163 8.824968 8.352701 7.827044 7.261489 6.669767 6.065306 5.460744 4.867524 4.295576 3.753114 3.246529 2.780379 2.357469 1.978997 1.644756 1.353366 1.102520 8.892320 7.100702 5.613648 4.393867 3.404918 2.612308 1.984269 1.492228 1.111037 8.189947 5.977133 4.318812 3.089554 2.188204 1.534407 1.065258 7.322023 4.982759 3.357159 2.239432 1.479001 9.670855 6.260771 4.012900 2.546580 1.600024 9.953292 6.130269 3.738234 2.256986 1.349177 7.985244 4.679385 2.715018 1.559705 8.871569 4.996307 2.786066 1.538262 |
. . 2区間の積分の場合は、著者の方法はステップ3)及び4)を2行3列の積分行列を使う修正処理に少し変更した数式で表された次の結果を与える。ステップ4)の y2 の式は半区間として h を使用し、2区間 2h を積分する Runge-K.法の結果と同じである。従って、数値解の比較は R.-K. 2 と行わねばならない。
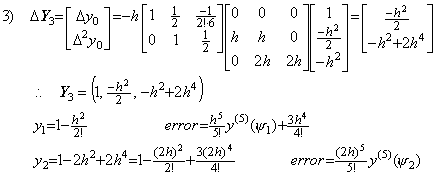
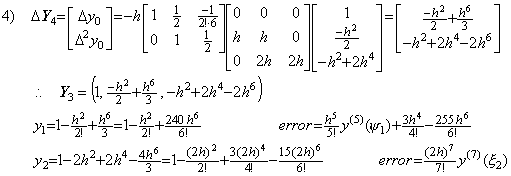
. . この方法に等価なプログラムは第2章1.3節に示されている。但し、ベクトル計算は使用していない。上記の微分方程式を零から6迄 30 等区分点を用いて解くために 56 行以降のサブルーチンを書き換えると、t=6 において y=1.522434×10−7 の結果を得る。この結果は著者の解法の1積分幅の半分を積分する表 1.1 の R.-K. 3 より精度が良い。これは Runge-K.法は数値計算ではより多くの誤差を生ずることを示す。
. . 著者の解法はステップ2), 3)及び4)の結果の y2 が解 y2 の収束又は積分幅の適否を判断できるデータであり、積分幅を可変にしてもっと正確な解を得ることができると言う理由でも従来の解法より優れている。著者の可変区分幅解法は第2章2.4節の表 2.7 に示すように t=13.0 において y=2.005017×10−36 の結果を与える。その解の真値は 2.00500878……×10−36 である。
1.3 Lipschitz 条件
. .
積分演算子値は一定値であるから(1.7)の左辺は次のようになる。
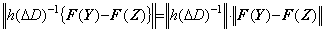
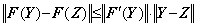 _________(1.17)
_________(1.17)(1.8)は |F' (Y)|≤k を満たす定数 k が存在することを必要とする。故に、ベクトル値関数 F(Y)又は関数 f(y) は Lipschitz 条件を満たさなければならない。しかし、Lipschitz 条件は厳密には(1.7)の導出過程により |F' (ξ)| の最大値又は |f ' (ξ)| の最大値であるから、y と z の間に平均値 |f ' (ξ)| の最大値が存在するなら関数 f(y) は f ' (y) の値が無限大となる点を持っても良い。
. . 微分方程式(1.18)は(1.19)に示すように f(y)、即ち、y' (y)が Lipschitz 条件を満たさないから数値計算では解くことが出来ないと言われる。
 __________(1.18)
__________(1.18)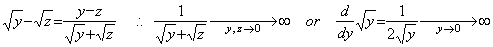 ____(1.19)
____(1.19)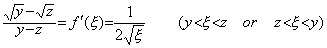
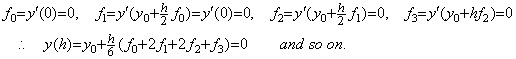
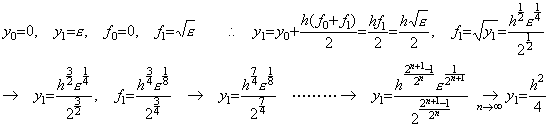
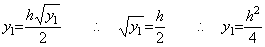 ______(1.20)
______(1.20)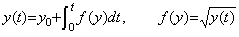 ________(1.21)
________(1.21). . (1.21)の方程式は不動点を持つために必要な条件、即ち、(1.8)を h の値に無関係に満たしている。y>ξ>z>0 と仮定すると、
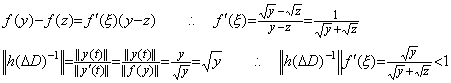
. . 著者の解法はステップ1)をとばしてステップ2)の被演算子として(1.20)の不動点を用いてこの微分方程式を解くことができる。
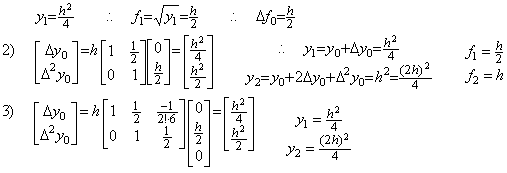
通常、微分方程式(1.18)の解は任意の定数 c に対して(1.22)であると言われる。
 ______(1.22)
______(1.22). . 上記の例は台形法の不動点が正確な解の場合である。不動点が近似解であっても著者の解法は数値的に正しい解を得ることができる。微分方程式(1.12)の場合には、台形法の不動点は h4 以上の項が正しくない級数で表される。
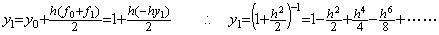
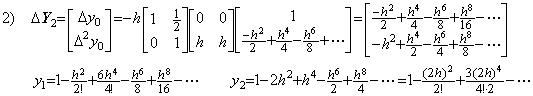
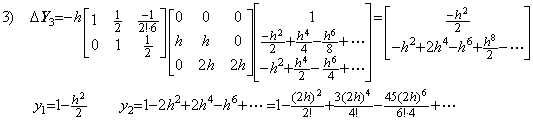
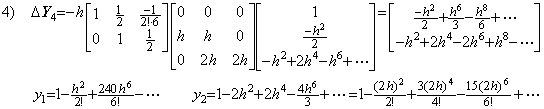
結果の y2 は h8 以上の項が数値的に無視できるなら前節最後のステップ4)の結果と同じである。
. . 数値解法は(1.23)の微分方程式を、f(0)が無限大であるから解くことが出来ない。この理由は Lipschitz 条件とは無関係である。何故なら、(1.24)に示すように yz≠0 なら平均値 f ' (ξ)が存在するからである。
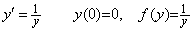 ________(1.23)
________(1.23)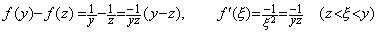 _____(1.24)
_____(1.24). . 台形法も、h が等区分幅のとき t=h において初期値 y0 が与えられれば、この微分方程式を解くことができる。t=2h における y1 の値を任意の値に仮定して、(1.25)の台形法を反復すると等区分幅が h=0.1 のとき解は表1.2 の A 欄に示すようになる。
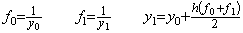 ______(1.25)
______(1.25)| 表 1.2__y0=y(0.1), h=0.1 | |||
|---|---|---|---|
| t | A | B | 真__値 |
| 0.1 0.2 0.3 0.4 0.5 : 1.0 2.0 3.0 4.0 5.0 : : 10.0 : : 100.0 |
0.447213 0.637454 0.779994 0.899673 1.00500 : 1.41819 2.00297 2.45196 2.83058 3.16421 : : 4.47352 : : 14.1426 |
0.450000 0.639319 0.781506 0.900981 1.00617 : 1.41902 2.00355 2.45243 2.83100 3.16459 : : 4.47378 : : 14.1427 |
(初 期 値) 0.6324555 0.7745966 0.8944271 1.0000000 : 1.4142135 2.0000000 2.4494897 2.8284271 3.1622776 : : 4.4721359 : : 14.142135 |
これらは yk に関する下記の方程式の不動点と同じである。
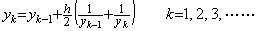 _____(1.26)
_____(1.26). . (1.25)の f0 と f1 の平均値は t=0.1 の近辺における積分の平均値とは大きく異なる。正確な平均値 f は以下に示すように f0 及び f1 の逆数により与えられる。(1.23)の微分方程式の両辺を逆数にして独立変数を y に代えると、
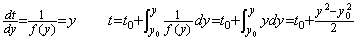
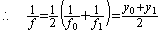 __________(1.27)
__________(1.27)| 0.4472136, 0.6708204, 0.6260990, 0.6335526, 0.6322675, 0.6324878, 0.6324500 0.6324565, 0.6324554, 0.6324556, 0.6324555 |
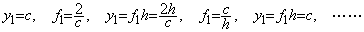
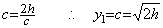 ________(1.28)
________(1.28)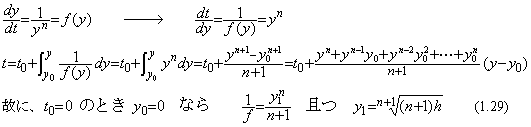
| 1) | 非常に小さな値 y=ε における解 t=δ を求める。 |
| 2) | 独立変数を t に代えて、f(y)を t=δ から t=h まで積分して解 y1 を得る。 |
| 3) | t=h における初期値 y1 で t=kh, (k>1) における解 yk を求める。 |
. . 微分方程式(1.23)の場合には、ε を 0.1 と仮定すると、中間点は y=0.05 で、ステップ1)は次の結果を与える。
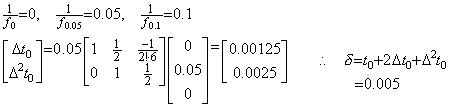
| 56 F=1/Y(1):RETURN 58 XB=0.005:XE=0.1:N=1:ND=1:Y(1)=0.1:EE=16:RETURN 60 Y#=SQR(X#):PRINT USING"True=##.########^^^^";Y#:RETURN |
. . ステップ 3)は表 1.4 に示すように t=0.1+kh における解 yk+1 を k=IB に対して与える。そのために第 58 行は次のようにする。
| 表 1.3__t=0.005 から 0.1 迄の解 | ||||
|---|---|---|---|---|
| EB | EE | t (10n) | y (10n) | 真 値 (10n) |
| 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 6 7 8 9 10 11 12 7 8 |
64 64 64 64 64 64 64 64 64 64 32 32 32 32 32 16 16 16 16 16 16 16 8 8 |
6.48438(-3) 7.96875(-3) 9.45313(-3) 0.0109375 0.0124219 0.0139062 0.0153906 0.016875 0.0183594 0.0198437 0.0228125 0.0257813 0.02875 0.0317187 0.0346875 0.040625 0.0465625 0.0525 0.0584375 0.064375 0.0703125 0.07625 0.088125 0.1 |
1.138805(-1) 1.262439(-1) 1.375001(-1) 1.479020(-1) 1.576190(-1) 1.667709(-1) 1.754459(-1) 1.837118(-1) 1.916214(-1) 1.992173(-1) 2.136001(-1) 2.270738(-1) 2.397916(-1) 2.518681(-1) 2.633914(-1) 2.850439(-1) 3.051640(-1) 3.240371(-1) 3.418699(-1) 3.588176(-1) 3.750001(-1) 3.905126(-1) 4.198215(-1) 4.472137(-1) |
1.13880419(-1) 1.26243811(-1) 1.37500002(-1) 1.47901993(-1) 1.57619004(-1) 1.66770799(-1) 1.75445862(-1) 1.83711734(-1) 1.91621377(-1) 1.99217217(-1) 2.13600096(-1) 2.27073783(-1) 2.39791578(-1) 2.51868019(-1) 2.63391346(-1) 2.85043851(-1) 3.05163891(-1) 3.24037030(-1) 3.41869859(-1) 3.58817497(-1) 3.75000000(-1) 3.90512488(-1) 4.19821403(-1) 4.47213599(-1) |
| 表 1.4__t=0.1 から 10 迄の解 | |||||
|---|---|---|---|---|---|
| IB | EB | EE | t | y (10n) | 真 値 (10n) |
| 1 | 1 2 3 4 5 6 4 |
8 8 8 8 8 8 4 |
0.1125 0.125 0.1375 0.15 0.1625 0.175 0.2 |
4.743421(-1) 5.000004(-1) 5.244048(-1) 5.477229(-1) 5.700880(-1) 5.916082(-1) 6.324558(-1) |
4.74341658(-1) 5.00000000(-1) 5.24404430(-1) 5.47722568(-1) 5.70087702(-1) 5.91607973(-1) 6.32455537(-1) |
| 2 | 1 2 3 4 |
4 4 4 4 |
0.225 0.25 0.275 0.3 |
6.708207(-1) 7.071070(-1) 7.416201(-1) 7.745969(-1) |
6.70820407(-1) 7.07106781(-1) 7.41619857(-1) 7.74596646(-1) |
| 3 | <1 2 2 |
4 4 2 |
0.325 0.35 0.4 |
8.062260(-1) 8.366602(-1) 8.944274(-1) |
8.06225760(-1) 8.36660019(-1) 8.94427164(-1) |
| 4 | 1 2 |
2 2 |
0.45 0.5 |
9.486835(-1) 1.000000 |
9.48683285(-1) 9.99999970(-1) |
| 5 | 1 2 |
2 2 |
0.55 0.6 |
1.048809 1.095445 |
1.04880880 1.09544508 |
| 6 | 1 2 |
2 2 |
0.65 0.7 |
1.140176 1.183216 |
1.14017540 1.18321595 |
| 7 8 9 19 29 39 49 59 69 79 89 99 |
1 1 1 1 1 1 1 1 1 1 1 1 |
1 1 1 1 1 1 1 1 1 1 1 1 |
0.8 0.9 1 2 3 4 5 6 7 8 9 10 |
1.264911 1.341641 1.414214 2.000000 2.449490 2.828427 3.162278 3.464102 3.741658 4.000001 4.242641 4.472137 |
1.26491107 1.34164077 1.41421356 1.99999994 2.44948965 2.82842704 3.16227751 3.46410148 3.74165726 3.99999988 4.24264069 4.47213595 |
1.4 内挿解法と外挿解法
. .
n 次の積分行列を使用する著者の解法は n+1 個の等間隔区分点を必要とする。1積分区間が与えられた積分範囲をその解を得るべき点の数で割ることにより与えられたとき、通常、これ等の点は前節で述べたように各積分区間を n で割ることにより得られる。故に、著者はそれらを内挿による解と呼ぶ。それは積分区間の中点の予測結果を使用する Runge-Kutta 法と類似である。但し、Runge-Kutta 法は著者の3点を使用する方法とは異なる予測結果を使用する点では異なる。
. .
内挿解法は各積分区間を細分した可変積分区間を使用し、可変次数の積分行列を使用して微分方程式を解くことができる。しかし、表に表された関数はそのデータ間隔を n 分割した等間隔点の関数値を得ることが出来ないから内挿解法で積分することは出来ない。この場合は、著者の解法は必要な n+1 個の等間隔区分点を得るために n 個の表データの区間を使用しなければならない。これ等の解は t=t0+h の解を修正するために k>1 に対する t=t0+kh の点を使用するので著者はこれらを外挿による解と呼ぶ。
. .
外挿解法は固定次数か可変次数の積分行列を使用することができる。両解法は積分の下限を進める二つの方法を使うことができる。積分行列が
. .
表 1.5 は微分方程式 y' =−ty, y(0)=10 を等間隔区分幅 h=0.1 及び可変次数 n≤11 の積分行列を使った外挿解法により解いた解を示す。欄 IB は等間隔区分点であり、欄 E は積分行列の次数、即ち、修正子は((E−1)×E)の次数である。IB が1のとき、t=0.1 における解は4点の等間隔区分点 t=0, 0.1, 0.2, 0.3 を用いて収束するが、t=0.2, 0.3 における解は収束していないので IB の値は1増加する。IB が2のとき、t=0.1 における解を初期値とした t=0.2, 0.3, 0.4, 0.5 における解は全て収束するので IB の値は4増加する。IB が 28 以上では、解は IB の値が示す点においてのみ収束する。IB が 52 以上では、積分行列の次数は与えられた制限により増加しない。この制限は解の精度を減少させる。しかし、その減少は表 1.1 に示した Milne 法及び Runge-Kutta 法に比べれば僅かである。
| 表 1.5 . .外挿解法による y' =−ty, y(0)=10 の解 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IB | E | t | y (10n) | 真 値 (10n) | . . | IB | E | t | y (10n) | 真 値 (10n) |
| 1 2 6 7 10 14 15 16 21 22 28 29 30 31 32 33 34 |
4 5 4 4 5 6 6 6 6 7 7 7 8 6 6 7 7 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 |
9.950120(0) 9.801984(0) 9.559971(0) 9.231160(0) 8.824965(0) 8.352683(0) 7.827014(0) 7.261469(0) 6.669735(0) 6.065274(0) 5.460716(0) 4.867497(0) 4.295553(0) 3.753093(0) 3.246508(0) 2.780359(0) 2.357449(0) 1.978977(0) 1.644736(0) 1.353346(0) 1.102500(0) 8.892118(-1) 7.100501(-1) 5.613449(-1) 4.393672(-1) 3.404729(-1) 2.612128(-1) 1.984100(-1) 1.492071(-1) 1.110894(-1) 8.188665(-2) 5.975999(-2) 4.317823(-2) 3.088704(-2) |
9.95012479(0) 9.80198673(0) 9.55997478(0) 9.23116344(0) 8.82496903(0) 8.35270199(0) 7.82704545(0) 7.26149030(0) 6.66976789(0) 6.06530660(0) 5.46074412(0) 4.86752228(0) 4.29557318(0) 3.75311111(0) 3.24652467(0) 2.78037290(0) 2.35746057(0) 1.97898674(0) 1.64474464(0) 1.35335283(0) 1.10250492(0) 8.89216081(-1) 7.10053615(-1) 5.61347500(-1) 4.39369336(-1) 3.40474421(-1) 2.61214065(-1) 1.98410974(-1) 1.49207819(-1) 1.11089965(-1) 8.18869738(-2) 5.97602198(-2) 4.31784069(-2) 3.08871441(-2) |
35 : : : : 51 52 53 54 55 56 57 58 59 60 61 : : 89 90 91 |
7 : : : : 10 11 11 11 11 11 11 11 11 11 11 : : 10 11 11 |
3.5 : : : : 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6.0 6.1 : : 8.9 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 9.8 9.9 10. |
2.187483(-02) : : : : 2.249050(-05) 1.343809(-05) 7.949373(-06) 4.655704(-06) 2.699572(-06) 1.549749(-06) 8.808157(-07) 4.956393(-07) 2.761235(-07) 1.522994(-07) 8.316679(-08) : : 6.306696(-17) 2.576850(-17) 1.042381(-17) 4.175947(-18) 1.660551(-18) 6.670604(-19) 3.025806(-19) 2.349915(-19) 4.096942(-19) 1.019628(-18) 2.731899(-18) 7.452993(-18) |
2.18749112(-02) : : : : 2.24905706(-05) 1.34381028(-05) 7.94938558(-06) 4.65571332(-06) 2.69957850(-06) 1.54975396(-06) 8.80816483(-07) 4.95639984(-07) 2.76124090(-07) 1.52299797(-07) 8.31670729(-08) : : 6.30615778(-17) 2.57675711(-17) 1.04240256(-17) 4.17501738(-18) 1.65551973(-18) 6.49931301(-19) 2.52616378(-19) 9.72094942(-20) 3.70353883(-20) 1.39694133(-20) 5.21670711(-21) 1.92874985(-21) | |
. . IB が 91 のとき、t=9.1 より後の全ての点における解は収束していると見なされる。その理由は、IB が 92 になると 9.1≤t≤10 の範囲には 11 個の等間隔区分点が存在しないからである。t=9.5 より後の解は正確な解とは大きく異なるが、これらは t=9.1 における解を収束させるために有用である。この現象は、表 1.6 に示すように IB が1だけ増加する場合は常に起こる。その解が t=5.2 で収束したとき、t=5.2 より後の解は収束しておらず、t=6 における解は表 1.1 の R.-K. 3 欄の結果と同じくらい不正確である。この理由により、Milne 法は後退補間公式で導かれた予測子を使い、最後の点における解を正確に予測できると言われる。しかし、この考えは間違いである。何故なら、Milne の予測子は前進補間公式により導かれた(1.14)と同じものである。又、高次多項式を用いる予測子・修正子法は不安定であるとも言われる。しかし、その原因は最後の点における解を予測し、修正することにある。
| 表 1.6 . .t=0 から 6 迄の解(h=0.1) | ||||
|---|---|---|---|---|
| IB | E | t | y (10−n) | 真 値 (10−n) |
: 46 47 48 49 50 51 52 |
: 9 9 10 10 10 10 10 |
: 4.6 4.7 4.8 4.9 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6.0 |
: 2.541928(-4) 1.596674(-4) 9.929478(-5) 6.113552(-5) 3.726643(-5) 2.249050(-5) 1.343809(-5) 7.949374(-6) 4.655708(-6) 2.699582(-6) 1.549770(-6) 8.808545(-7) 4.957133(-7) 2.762749(-7) 1.526310(-7) |
: 2.54193577(-4) 1.59667624(-4) 9.92949522(-5) 6.11356511(-5) 3.72665317(-5) 2.24905706(-5) 1.34381028(-5) 7.94938558(-5) 4.65571332(-6) 2.69957850(-6) 1.54975396(-6) 8.80816483(-7) 4.95639984(-7) 2.76124090(-7) 1.52299797(-7) |
. . 悪条件の微分方程式を解く数値解法は次の条件を満たさなければならない。それらが内挿補間による解法を使うものであるなら、等間隔区分幅は可変でなければならず、積分行列は可変次数でも固定次数でも良い。解が収束しているか否かは最後の点で判断しなければならない。それらが外挿補間による解法を使うものなら、積分行列は可変次数でなければならない。解が収束しているか否かは初期値点の次の点で判断しなければならない。解が引き続く k 点で収束しているときは次のステップは初期値点を k 番目の点まで進めてよい。
1.5 ベクトル関数の Taylor 展開
. .
微分方程式を著者の演算子法でベクトルコンピュータを使って解くために、微分方程式 y' =f(y)のベクトル値関数 F(Y)はベクトル Y を直接に使って計算されなければならない。通常のコンピュータの場合には、このベクトル値は等間隔区分点においてベクトル Y から変換された解の値 yk に対応する関数値 fk の逐次階差を計算することにより得ることができる。この場合、その計算が逐次階差に多くの有効桁桁落ちを惹き起こすなら、解は十分な精度を得られないであろう。それを避けるためには、ベクトル値関数はベクトル Y から直接に計算されるべきである。従って、F(Y)は1.2節で述べたベクトル関数でなければならない。その関数が無理関数なら通常 Taylor 展開により計算される。
. .
各等間隔区分点 tk=t0+kh, (k≥0)において関数 f(t)の Taylor 展開を実行し、その各 Taylor 展開の t=tk+h における値 f(tk+h)と初期値 f(tk)の差分を計算すると、
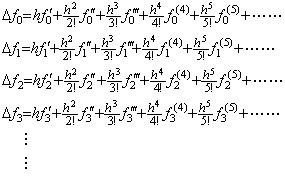
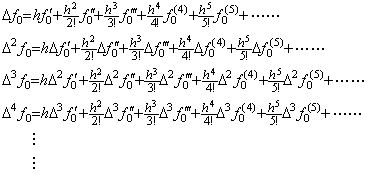
. .
[定理 401] f(t)∈Cp+1[a, b]のとき、関数 Δf(t)を表すベクトル ΔF の Taylor 展開は次のように表される。
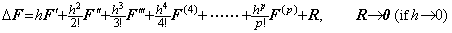 _____(1.30)
_____(1.30)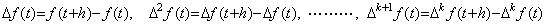
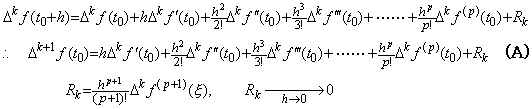
. .
従って、関数 f(y)が y の無理関数なら、微分方程式 Y' =F は(1.30)の F に代入すれば(p+1)階の微分方程式に等価である。しかし、f(y(t)) の逐次導関数が y に無関係なら、その微分方程式は一階の微分方程式として解くことができる。その例は第 1.3 節の(1.18)の微分方程式である。
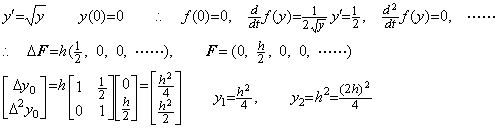 . .(1.31)
. .(1.31)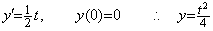
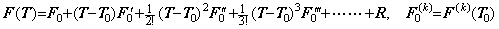 ____(1.32)
____(1.32). . ベクトル T0 が関数 t(u)を表し、ベクトル T が関数 t(u)+h を表すとき、ベクトル T は t0+h, t1+h, t2+h, ………, tm+h の逐次階差からなる。故に、
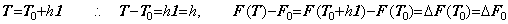
. . ベクトル T が u0 から um 迄の関数 t(u)を表し、ベクトル T0 が定数関数 t=t(u0)=t0を表すとき、
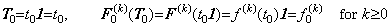
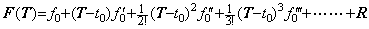 ____(1.33)
____(1.33). . 関数 t(u)が t(u)=t0+hu なる関数のとき、等間隔点 u=0, 1, 2, 3, ……… に対する t(u)の値も等間隔であり、関数 t(u)はベクトル T=(t0, h, 0, 0, ………)で表される。故に、
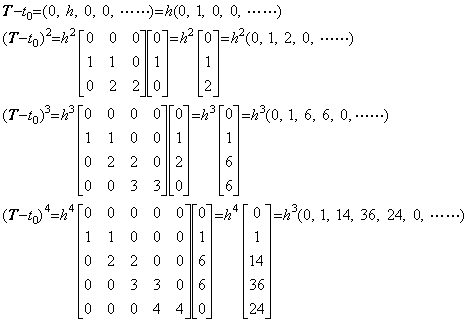
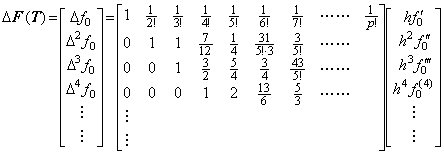 __(1.34)
__(1.34)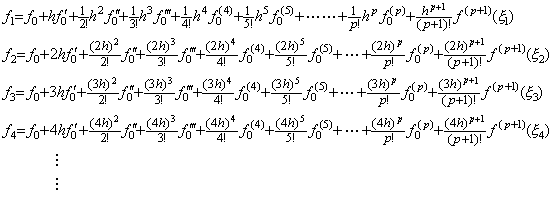
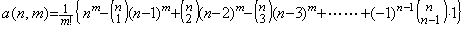 ___(1.35)
___(1.35)但し、 _____n, m=1, 2, 3, 4, ………
. .
[定理 402]. .m≥n+1 の場合は、
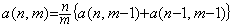 ______(1.36)
______(1.36)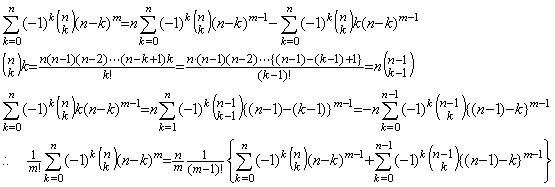
| [Q.E.D.] |
. . 微分方程式(1.31)の場合には、f0", f0(3), f0(4), ……… の値は全て零であるから行列演算式(1.34)は次のようになる。
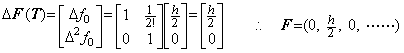
. . 一般に、微分方程式が微分可能なら逐次の整数 k に対する初期値 y0(k) を得ることができ、解 y(t)は積分することなく Taylor 展開で得ることができる。数値解も(1.34)の行列演算式で記号 F 及び f をそれぞれ Y 及び y に置き換えて得ることができる。従って、微分方程式の数値解が存在することは Taylor 展開の収束に等価である。
. . y' =f(y) で表される一階の微分方程式を反復積分により解くとき、関数 f(y)が無理関数なら独立変数 y の関数である Taylor 展開で表して良い。ベクトル関数 F(Y)は記号 T 及び t をそれぞれ Y 及び y で置き換えることにより(1.37)で表される。
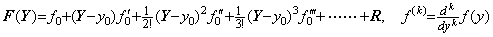 ____(1.37)
____(1.37)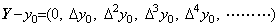
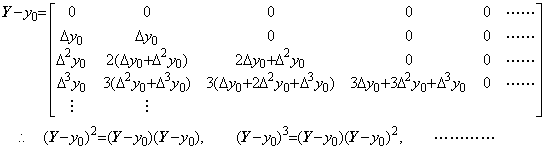
. . 関数 y(t)及び f(y)が(1.38)であるとき、
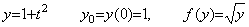 ______(1.38)
______(1.38)
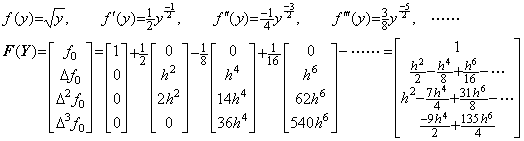 __(1.39)
__(1.39)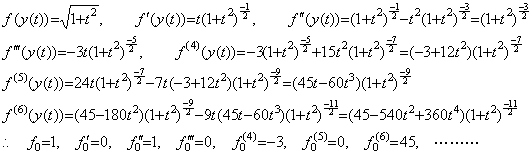
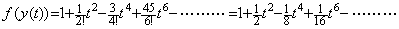 ____(1.40)
____(1.40)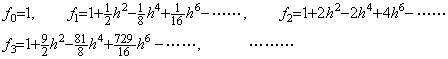
1.6 Newton-Raphson 法
. .
ある数 y の平方根を x で表すと、それは関数 f(x)=x2−y の曲線が x 軸と交わる点で与えられる。同様に、あるベクトル Y の平方根をベクトル X で表すと、それは、ベクトルの順序対(X, F)の全てを意味する平面でベクトル関数 F(X)=X2−Y の曲線が X 軸と交わる点で与えられる。その点は Newton-Raphson 法で得ることができる。
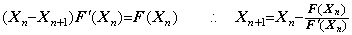 _____(1.41)
_____(1.41)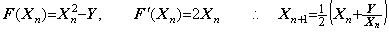 ___(1.42)
___(1.42)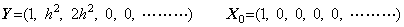
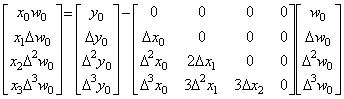 ____(1.43)
____(1.43)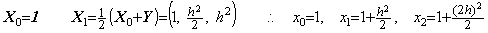
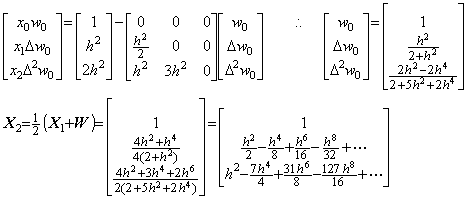
1.7 微分及び積分の公式
. .
著者の微積分演算子は微分方程式を解くために記号演算子として使うことができる。その場合、第二章2.2節に述べたように、演算子とベクトルの積は数の積と同じ交換則及び結合側が必ずしも成立しないことに注意しなければならない。第1.3節の(1.18)の微分方程式は関数 y の平方根を使わずに両辺を自乗して解くことができる。
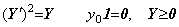 ________(1.44)
________(1.44)
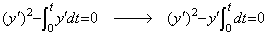
. .
[定理 403]. .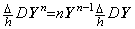 ________(1.45)
________(1.45)
[証明]. . yn(t)の導関数は次のようになる。
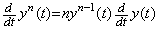
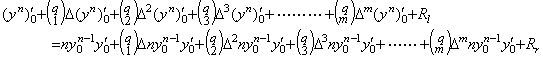
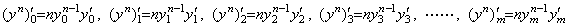
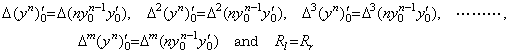
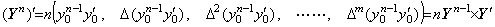 ____[Q.E.D.]
____[Q.E.D.]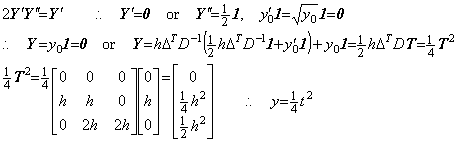
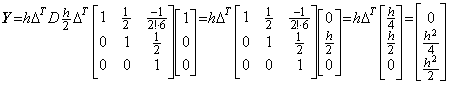
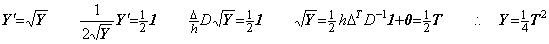
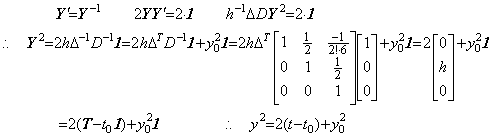
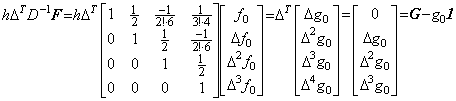 ____(1.46)
____(1.46)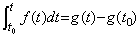 ________(1.47)
________(1.47). . 不定積分は微分方程式の解が無数にあることを意味するのではなく、初期値が不明であることを意味する。従って、積分演算は一意である。微分演算は任意の定数 c を持つ全ての関数、即ち、g(t)+c から一つの導関数 g' (t)を得ると言われる。しかし、著者は、微分演算は初期値と導関数の対、即ち、(g(0), g' (t))を得るのであり、それぞれの c の値に対する微積分演算は一意に可逆であると主張する。
. .
[定理 404]. .
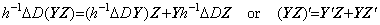 ______(1.48)
______(1.48)
[証明]. .二つの関数の積 y(t)z(t)の導関数は(yz)' =y' z+yz' である。この等式を Newton の補間公式で表すと、定理403 の証明と同じ方法でベクトルの等式(1.48)で表される。_______________[Q.E.D.]
. .
[定理 405]. .
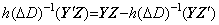 ________(1.49)
________(1.49)
[証明] (1.48)の両辺を積分することにより明らかである。__________[Q.E.D.]
. .
微分方程式 y' =y−1, y(t0)=y0 は定理405により次のように解ける。
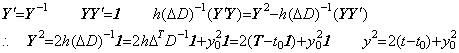
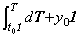
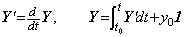
. .
[定理 406]. . Y=eT のとき、 その導関数は Y' =eT である。
[証明]. . y=et 及び y' =et により明らかである。__________[Q.E.D.]
. .
ベクトル関数 eT は Taylor 展開で次のように表される。
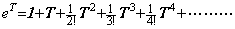 ________(1.50)
________(1.50)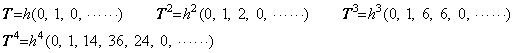
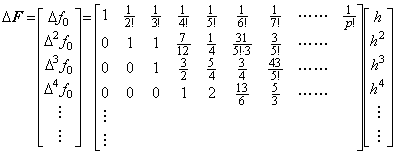 ____(1.51)
____(1.51)