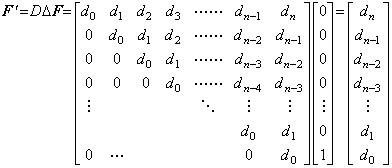|
4.. . Introducing the integral operator.
4.1. .Summary explanation of the integral operator.
. .
The differentiable function y(t) is expressed in the integral from t0 to t of the derivative y' (t) as follows, where y0 denotes the value y(t0).
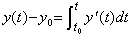 ______(4.1)
The successive differences are obtained by use of the values at the equidistant points t=t0+qh as follows. ______(4.1)
The successive differences are obtained by use of the values at the equidistant points t=t0+qh as follows.
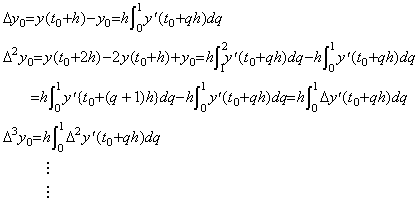 . .If the value h is very small, these integrands are nearly equal to the constants y0', Δy0', Δ2y0', ……… for 0≤q≤1. Accordingly, Eq.(4.1) may be expressed in the matrix equation ΔY=hAY ', where the character A denotes a matrix. The value y0 of the left side of Eq.(4.1) at t=t0 does not appear on the matrix equation, because it is not the result of the integral operation. The matrix A is not the expansion of a vector because the integration is not a function. It is a quotient without vector form or an operator other than quotient. Hence it is not able to calculate the matrix A by the vectors ΔY and Y ' of only a function. It must be calculated by use of the vectors of all the differentiable functions and the first derivatives.
. .If the value h is very small, these integrands are nearly equal to the constants y0', Δy0', Δ2y0', ……… for 0≤q≤1. Accordingly, Eq.(4.1) may be expressed in the matrix equation ΔY=hAY ', where the character A denotes a matrix. The value y0 of the left side of Eq.(4.1) at t=t0 does not appear on the matrix equation, because it is not the result of the integral operation. The matrix A is not the expansion of a vector because the integration is not a function. It is a quotient without vector form or an operator other than quotient. Hence it is not able to calculate the matrix A by the vectors ΔY and Y ' of only a function. It must be calculated by use of the vectors of all the differentiable functions and the first derivatives.
. .
If the derivative is constant, that is, y' (t)=c1, Eq.(4.1) comes to y(t)−y0=c1t and the successive difference is only Δy0=c1h. Hence the matrix equation is c1h1=hAc11. It requires the first column of the matrix to have the elements which are all zero except the first element is one.
. .
If the derivative is y' (t)=c1+2c2t, Eq.(4.1) comes to y(t)−y0=c1t+c2t2. Hence the matrix equation is,
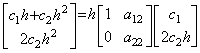 It requires the second column of the matrix to have a12=1/2, a22=1 and the other elements which are all zero.
It requires the second column of the matrix to have a12=1/2, a22=1 and the other elements which are all zero.
. .
If the derivative is y' (t)=c1+2c2t+3c3t2, Eq.(4.1) comes to y(t)−y0=c1t+c2t2+c3t3. Hence,
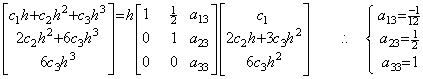 . .The more iteration give the triangular matrix A which has the first row expressed below and the other rows whose elements are of the same as the upper row except those are shifted to the right by one cell.
. .The more iteration give the triangular matrix A which has the first row expressed below and the other rows whose elements are of the same as the upper row except those are shifted to the right by one cell.
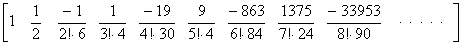 . .The matrix is the inverse matrix of the differential matrix D. Hence the integral in Eq.(4.1) may be expressed in,
. .The matrix is the inverse matrix of the differential matrix D. Hence the integral in Eq.(4.1) may be expressed in,
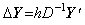 _______(4.2)
However, it is hard to make the proof that the matrix is held for all the integrable functions. The proof can be made by use of Newton's interpolation formula with remainder term and its integral, if the integrated functions are the continuous (p+1)th differentiable functions. It is shown in following sections. _______(4.2)
However, it is hard to make the proof that the matrix is held for all the integrable functions. The proof can be made by use of Newton's interpolation formula with remainder term and its integral, if the integrated functions are the continuous (p+1)th differentiable functions. It is shown in following sections.
. .
The author said the differential operator was Δh−1D in Section 3.5. However, supposing the operand is ΔY, the differential operator comes to h−1D and Eq.(4.2) comes to the inverse operation of the differentiation. The idea will solve the trouble of usual differential operator. If the function is constant, because of the operand ΔY =0, the derivative comes to Y ' =0.
. .
In case of usual differentiation too, it should be the inverse operation of Eq.(4.1). Accordingly, the operand of differentiation should be y(t)−y0. The definition of differentiation is expressed in,
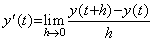 _______(4.3)
In case that the function y(t) is constant, the derivative y' (t) comes to zero for arbitrary h value. The reason is that the operand of the operator lim is identical with zero. Furthermore it is able to consider the above definition as the simplified definition of Eq. (4.4), so the operand of differentiation is y(t)−y0 and identical with zero. _______(4.3)
In case that the function y(t) is constant, the derivative y' (t) comes to zero for arbitrary h value. The reason is that the operand of the operator lim is identical with zero. Furthermore it is able to consider the above definition as the simplified definition of Eq. (4.4), so the operand of differentiation is y(t)−y0 and identical with zero.
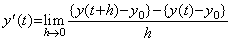 ______(4.4)
. .In usual definition, the integral operation includes the operation adding arbitrary constant c. Hence the integration is expressed in, ______(4.4)
. .In usual definition, the integral operation includes the operation adding arbitrary constant c. Hence the integration is expressed in,
 ______(4.5)
In this case, the value y(t0) is the result of the integral operation in Eq. (4.5) because the operation adding an indefinite constant is also carried out at t=t0. Hence the integral operator must be considered as the complex operator including the adding operator. In this operational calculus, the result vector Y has the constant as the first component. It is expressed in the matrix equation by multiplying Eq.(4.2) by ΔT and adding the constant vector c1 to it as follows. ______(4.5)
In this case, the value y(t0) is the result of the integral operation in Eq. (4.5) because the operation adding an indefinite constant is also carried out at t=t0. Hence the integral operator must be considered as the complex operator including the adding operator. In this operational calculus, the result vector Y has the constant as the first component. It is expressed in the matrix equation by multiplying Eq.(4.2) by ΔT and adding the constant vector c1 to it as follows.
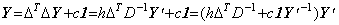 ____(4.6)
The integral operator has an indefinite operator, which is not vector and is denoted by the second term in parentheses as a matter of form. ____(4.6)
The integral operator has an indefinite operator, which is not vector and is denoted by the second term in parentheses as a matter of form.
. .
If the constant is y0=y(t0), Eq.(4.5) comes to the solution of the differential equation. In this case, the constant vector y01 must be expressed in the rigorous form which shows the constant y0 is the first element of the vector Y before differentiation. It is expressed in U0Y, where U0 is the matrix unit, which has the value 1 at the first element of the first row and is mentioned in Section 2.4 The summation operator. Accordingly, Eq.(4.6) is expressed in rigorous form by use of Δ−1 defined in Section 2.4.
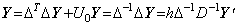 ______(4.7). .
The differential operator h−1D operates the operand ΔY, which has not the initial value y0. Hence it does not operate the initial value. The inverse operator is hD−1 and the result of the operation is ΔY uniquely. The differential operator Δh−1D gives the same derivative as the operator h−1D does but it operates the initial value y0 because the operand is the vector Y. This operator transforms the vector Y into the differential equation. Hence the initial value is held as it is and must be described with the differential equation. The inverse operator is hΔ−1D−1 and the result is Y uniquely. ______(4.7). .
The differential operator h−1D operates the operand ΔY, which has not the initial value y0. Hence it does not operate the initial value. The inverse operator is hD−1 and the result of the operation is ΔY uniquely. The differential operator Δh−1D gives the same derivative as the operator h−1D does but it operates the initial value y0 because the operand is the vector Y. This operator transforms the vector Y into the differential equation. Hence the initial value is held as it is and must be described with the differential equation. The inverse operator is hΔ−1D−1 and the result is Y uniquely.
. .
Usual differentiation does not distinguish these two operations so it has some troubles. The troubles will be solved by making distinction between the definitions in Eq.(4.3) and Eq.(4.4). The derivative y' (t) should be defined by Eq.(4.4) so the differentiation may be denoted by d(y-y0)/dt and the inverse operation is expressed in Eq.(4.1). The definition by Eq. (4.3) may be denoted by dy/dt and this differentiation operates the initial value y0. However, it dose not change the value and constructs the pair of the derivative and the initial value, that is, it transforms the function y(t) into the differential equation. The inverse operation is expressed in Eq.(4.5) with c=y(t0).
. .
The Laplace transform defines the differential operator by the operation for L{y(t)−y(0)} as follows, where the symbol L denotes the Laplace transformation.
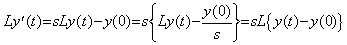 Hence the inverse operation must give L{y(t)−y(0)}. However it transposes sLy(0) to the opposite side and multiplies the both sides by s−1 as follows.
Hence the inverse operation must give L{y(t)−y(0)}. However it transposes sLy(0) to the opposite side and multiplies the both sides by s−1 as follows.
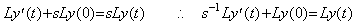 It is equivalent to Eq.(4.5) with t0=0 and c=y(0). These relation between the operator s and the operator s−1 are not shown explicitly in usual definition.
It is equivalent to Eq.(4.5) with t0=0 and c=y(0). These relation between the operator s and the operator s−1 are not shown explicitly in usual definition.
. .
Supposing all the functions and derivatives are defined by y(t)u(t), y' (t)u(t), y"(t)u(t), ………, y(n)(t)u(t), where u(t) is the unit step function, it does not need to distinguish the two differential operations because the differentiation holds the initial value y0 as the continuous differentiable impulse function y0δ(t), which was mentioned in Chapter 2 Section 3.2 but was not the Dirac delta function. Laplace transform treats these functions but usually omits u(t) from the expression of these functions. The rigorous Laplace transform expressing u(t) explicitly was mentioned in Chapter 2 Section 3.4 Laplace transform of any function.
. .
Mikusinski's operational calculus also treats these functions but it denotes the functions by {y(t)}, {y' (t)}, {y"(t)}, …… and the impulse function y0δ(t) as the numeric operator y0. The differential and integral operations are equivalent to following equations.
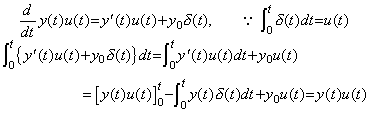 If (d/dt)y(t)u(t) is identical with zero, the operand y(t)u(t) is identical with zero. The derivative y' (t)u(t) must be obtained by transposing y0δ(t) to the left side. Hence the operand of the differentiation comes to y(t)u(t)−y0u(t) in the case too.
If (d/dt)y(t)u(t) is identical with zero, the operand y(t)u(t) is identical with zero. The derivative y' (t)u(t) must be obtained by transposing y0δ(t) to the left side. Hence the operand of the differentiation comes to y(t)u(t)−y0u(t) in the case too.
. .
The author's operational calculus is based on Newton's interpolation formula, which can not express the phenomena of u(t) starting up at t=0. Hence the two differential operations and the inverse operations must be distinguished. The operator hΔ−1D−1 gives the solution of the differential equation theoretically. However, in practical calculus, Eq.(4.7) is changed to Eq.(4.2) by multiplying the both sides by Δ and after ΔY has been obtained, the solution Y is obtained by use of Y=ΔTΔY+U0Y in Eq.(4.7).
4.2. .The integral of Newton's interpolation formula.
. .
In introducing the differential operator, the author treated the differentiation of the functions which are of the continuous (p+1)th differentiable functions. In introducing the integral operator, the integrands must be of the continuous p-th differentiable functions, because the integral is the inverse operation of the differential operation. Hence this section obtains the integral formula of y' (t) expressed in Newton's interpolation formula Eq.(3.21) in Section 3.4. The usual integral formula is expressed in use of Newton's interpolation formula of a function f(t) such that f(t)∈Cp+1[a, b]. The formula is obtained by substituting p+1, f for p, y' respectively and the result y(t) comes to the continuous (p+2)th differentiable function. . .
[Theorem 4.1]. .When y' (t)∈Cp[a, b], integrating it from tm to tm+1, where the limits are equidistant points expressed in tm=t0+mh for any integer m,
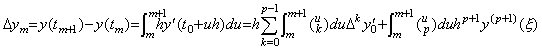 ____(4.8)
where ξ is a value which gives the remainder of the interpolation of y' (t) for a value q such that m<q<m+1. ____(4.8)
where ξ is a value which gives the remainder of the interpolation of y' (t) for a value q such that m<q<m+1.
[Proof]. .Substituting t=t0+uh,
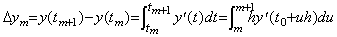 As mentioned in Section 3.4, expressing the derivative y' (t) in Eq.(3.22), the residual F(u) is expressed in Eq.(3.23), when the approximate formula has the constant Rq which is the R value of the remainder of Eq.(3.22) for a value q. These are given below.
As mentioned in Section 3.4, expressing the derivative y' (t) in Eq.(3.22), the residual F(u) is expressed in Eq.(3.23), when the approximate formula has the constant Rq which is the R value of the remainder of Eq.(3.22) for a value q. These are given below.
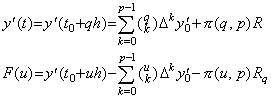 When the value q satisfies m<q<m+1, the residual F(u) is approximately expressed in Fig 3.1 of Section 3.2 around the range [m, m+1]. Hence there exists a value q such that the integral from m to m+1 of the residual F(u) comes to zero and there exists an approximate formula whose R value in the remainder is the constant Rq, which is the value for the value q. In the case,
When the value q satisfies m<q<m+1, the residual F(u) is approximately expressed in Fig 3.1 of Section 3.2 around the range [m, m+1]. Hence there exists a value q such that the integral from m to m+1 of the residual F(u) comes to zero and there exists an approximate formula whose R value in the remainder is the constant Rq, which is the value for the value q. In the case,
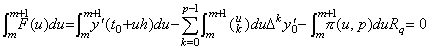 ____(4.9)
There exists a value ξ=t0+uh such that F(p)(u)=0 is satisfied for the value q. Hence, ____(4.9)
There exists a value ξ=t0+uh such that F(p)(u)=0 is satisfied for the value q. Hence,
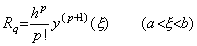 Therefore, multiplying Eq.(4.9) by h, Eq.(4.8) is obtained._________[Q.E.D.]
Therefore, multiplying Eq.(4.9) by h, Eq.(4.8) is obtained._________[Q.E.D.]. .
[Theorem 4.2]
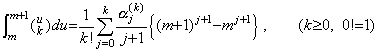 ____(4.10)
[Proof]. .By Theorem 3.27, ____(4.10)
[Proof]. .By Theorem 3.27,
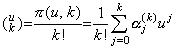 ______and______ ______and______
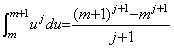 | [Q.E.D.] |
. .Substituting m=0 into Eq.(4.8), it is the formula obtaining Δy0, that is, the integral from t0 to t0+h of Newton's interpolation formula with the remainder. The coefficient of every term is expressed in Eq.(4.11) substituted m=0 into Eq.(4.10) and denoted by ak.
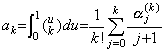 ______(4.11)
The sum of the right side means the product of the matrix expressed in Table 3.3 of Section 3.7 and the vertical vector whose components are 1/(j+1) as follows, where the matrix has zero in all the null cells of Table 3.3. ______(4.11)
The sum of the right side means the product of the matrix expressed in Table 3.3 of Section 3.7 and the vertical vector whose components are 1/(j+1) as follows, where the matrix has zero in all the null cells of Table 3.3.
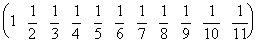 Accordingly, the coefficients ak for k=0 to 10 come to,
Accordingly, the coefficients ak for k=0 to 10 come to,
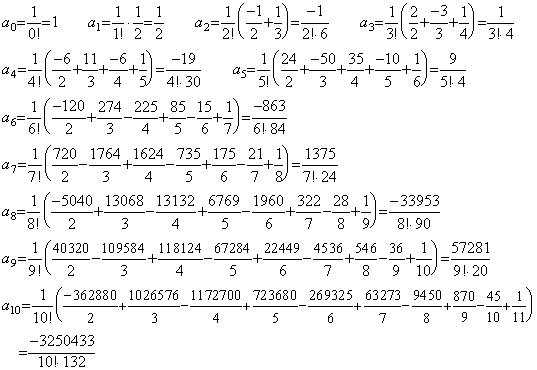
. .
Hence Eq.(4.8) comes to Eq.(4.12) when m=0, where ξ0 denotes the ξ value for the value q such that 0<q<1.
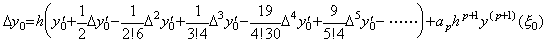 ____(4.12)
In the case m≥1, it is also able to calculate the coefficients of Eq.(4.8) by use of Eq.(4.10) and Table 3.3. However it is easier to use the following theorem. ____(4.12)
In the case m≥1, it is also able to calculate the coefficients of Eq.(4.8) by use of Eq.(4.10) and Table 3.3. However it is easier to use the following theorem.. .
[Theorem 4.3]
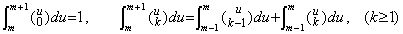 ____(4.13)
[Proof]. .If k=0, ____(4.13)
[Proof]. .If k=0,
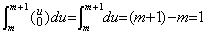 If k≥1, substituting u−1=v,
If k≥1, substituting u−1=v,
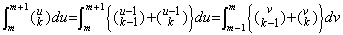 |
[Q.E.D.] |
. .
Accordingly, the n-th coefficient of Δy1 expressed in Eq.(4.8) is obtained by the sum of the (n−1)th and n-th coefficients of Δy0, where n≥2. The coefficients of Δy2 are also obtained by use of the coefficients of Δy1 in a similar way. Hence it is able to obtain the p integral formulas of the equidistant intervals from [t0, t1] to [tp−1, tp] successively, starting from Eq.(4.12).
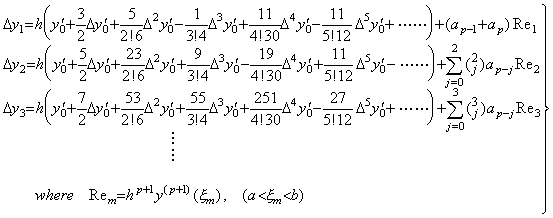 (4.14) (4.14)
4.3 The remainder of Simpson's 1/3 rule.
. .
Changing the integral interval of Eq.(4.9) with the two intervals from t0 to t2,
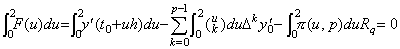 ____(4.15) ____(4.15)
where ____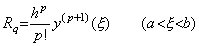 Therefore the integral formula from t0 to t2 of Newtorn's interpolation formula will come to,
Therefore the integral formula from t0 to t2 of Newtorn's interpolation formula will come to,
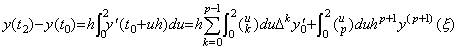 _____(4.16)
The coefficients expressed in integral in the right side are obtained by changing the integral interval of Eq.(4.10) with the two intervals from m to m+2 and substituting zero for m. Hence, _____(4.16)
The coefficients expressed in integral in the right side are obtained by changing the integral interval of Eq.(4.10) with the two intervals from m to m+2 and substituting zero for m. Hence,
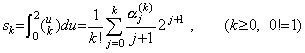 Using Table 3.3 Stirling's numbers of the first kind in Section 3.7, the values sk come to,
Using Table 3.3 Stirling's numbers of the first kind in Section 3.7, the values sk come to,
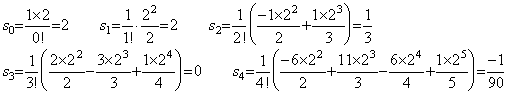 Hence Eq.(4.16) comes to Simpson's 1/3 rule with remainder in case of p=4.
Hence Eq.(4.16) comes to Simpson's 1/3 rule with remainder in case of p=4.
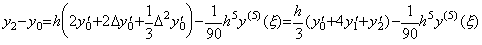 ____(4.17)
Usually the integrand is not denoted by the derivative form so denoting y' by f, the remainder is expressed by use of f(4)(ξ) instead of y(5)(ξ). ____(4.17)
Usually the integrand is not denoted by the derivative form so denoting y' by f, the remainder is expressed by use of f(4)(ξ) instead of y(5)(ξ).
. .
It is well known as the remainder of Simpson's 1/3 rule but it is not correct rigorously speaking. Simpson's 1/3 rule has no effect of the third difference as shown in Eq.(4.17). Accordingly, it is applicable to the function f(t) whose third derivative is not continuously differentiable. In the case there does not exist the value ξ by which the above remainder gives the correct value. For example, letting the function be,
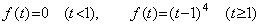 _____(4.18)
The integral from zero to two, Simpson's 1/3 rule by h=1, the correct remainder and the remainder of Eq.(4.17) are shown as follows. _____(4.18)
The integral from zero to two, Simpson's 1/3 rule by h=1, the correct remainder and the remainder of Eq.(4.17) are shown as follows.
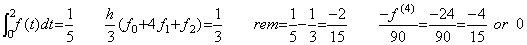 Hence there does not exist the value ξ such that −f(4)/90=−2/15 is satisfied. If f(t) is also (t−1)4 for t<1, there exists a value ξ such that the remainder gives the correct estimation.
Hence there does not exist the value ξ such that −f(4)/90=−2/15 is satisfied. If f(t) is also (t−1)4 for t<1, there exists a value ξ such that the remainder gives the correct estimation.
. .
The cause of the trouble is the assumption that the fourth derivative is continuous and that there exists a value q such that the integral of the residual in Eq.(4.15) is satisfied. All the usual proof of the remainder uses this assumption. Even if the fourth derivative is continuous, there does not exist a value q such that the integral of the residual F(u) comes to zero in case of the integral of two intervals. The reason is below.
 . .
The residual F(u) has the zero value for u=q and increases in the absolute value by increasing in |u−q|, because the constant Rq increases in the difference from the R value for any u. However it comes to zero at the equidistant points because of multiplying the difference by π(u, p). Hence the graph of the residual F(u) will summarily be expressed in Fig. 4.1. The amplitude of the graph is smallest in the interval where the point q exists and it becomes greater in the far interval. Accordingly, in case of the integral of one interval of F(u), there surely exists a value q such that the integral comes to zero but there does not exist such a value q in case of the integral of two intervals. In case of the integral of three intervals, there may exist such a value q but it is not sure. In case of the integral of four intervals, there will not exist such a value q. . .
The residual F(u) has the zero value for u=q and increases in the absolute value by increasing in |u−q|, because the constant Rq increases in the difference from the R value for any u. However it comes to zero at the equidistant points because of multiplying the difference by π(u, p). Hence the graph of the residual F(u) will summarily be expressed in Fig. 4.1. The amplitude of the graph is smallest in the interval where the point q exists and it becomes greater in the far interval. Accordingly, in case of the integral of one interval of F(u), there surely exists a value q such that the integral comes to zero but there does not exist such a value q in case of the integral of two intervals. In case of the integral of three intervals, there may exist such a value q but it is not sure. In case of the integral of four intervals, there will not exist such a value q.
. .
However, in case that the residual F(u) comes to zero at the point q' symmetric for q with respect to the point m+1, there exists the point q by which the integral of two intervals of F(u) comes to zero. Speaking the other way, if there exists a point q by which the integral of two intervals of F(u) comes to zero, the residual F(u) also must come to zero at the point q' symmetric for q with respect to the point m+1. Accordingly, the remainder of the interpolation formula of the integrand y' comes to zero at the p+2 points which are the p points from t0 to tp−1 and two points of q and q'. The integrand π(u, p) of the remainder of Eq. (4.15) is changed to π(u, p+1). The expression p in the upper limit of Σ and in the equation giving the constant Rq of remainder are also changed to p+1, provided that the derivative y' is the continuous (p+1)th differentiable function and not the continuous p-th differentiable function. The integral formula is expressed in Eq. (4.19), changing p in Eq. (4.16) to p+1.
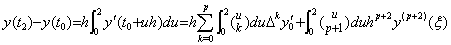 ____(4.19)
Simpson's 1/3 rule is the case of p=3 and not p=4, the successive differences exist up to the second derivative because of the coefficient s3=0, and the remainder term is s4h5y(5)(ξ) because of p+1=4 and p+2=5. Hence, it comes to the same formula as Eq. (4.17). Denoting y' by f, the remainder term is expressed by use of f(4)(ξ). It is evident that the both of integrand and integrated result have not the third difference when the approximation of function uses only 3 points. ____(4.19)
Simpson's 1/3 rule is the case of p=3 and not p=4, the successive differences exist up to the second derivative because of the coefficient s3=0, and the remainder term is s4h5y(5)(ξ) because of p+1=4 and p+2=5. Hence, it comes to the same formula as Eq. (4.17). Denoting y' by f, the remainder term is expressed by use of f(4)(ξ). It is evident that the both of integrand and integrated result have not the third difference when the approximation of function uses only 3 points.
. .
Still, there exist some trouble. The remainder is given by the constant Rq in the remainder of the residual F(u) and the constant is what has p+1 instead of p of Rq in Eq. (4.15) and what is substituted p=3. Accordingly, the residual F(u) comes to (4.20).
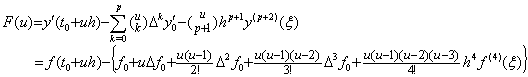 ___(4.20)
When the integrand is f(t)=t4 for t≥0, the integral from t=0 to t=2, Simpson's 1/3 rule without remainder by h=1, the remainder by both, the constant Rq, the successive differences, the residual F(u) are shown below. ___(4.20)
When the integrand is f(t)=t4 for t≥0, the integral from t=0 to t=2, Simpson's 1/3 rule without remainder by h=1, the remainder by both, the constant Rq, the successive differences, the residual F(u) are shown below.
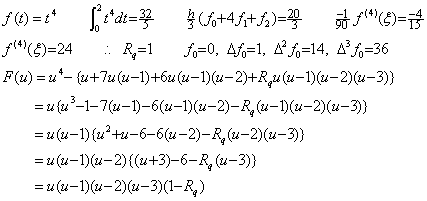 The residual F(u) becomes zero at the equidistant point u=0, 1, 2 and u=3 outside of the integral range, but there does not exist more one point. In this case, there does not exist trouble by the reason that the residual F(u) is identical with zero, because f(4)(t) and the value Rq are constant everywhere.
The residual F(u) becomes zero at the equidistant point u=0, 1, 2 and u=3 outside of the integral range, but there does not exist more one point. In this case, there does not exist trouble by the reason that the residual F(u) is identical with zero, because f(4)(t) and the value Rq are constant everywhere.
. .
When the integrand is f(t)=t5 for t≥0, the integral from t=0 to t=2, Simpson's 1/3 rule without remainder by h=1, the remainder by both, the constant Rq, the successive differences, the residual F(u) are shown below.
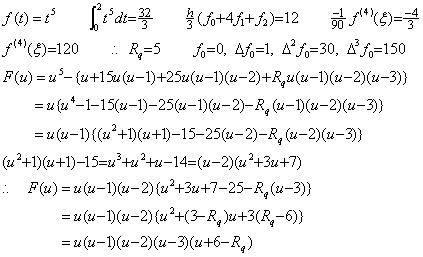 . .
The residual F(u) becomes zero at two points of u=3 and u=−1 together with the three equidistant points. The function (u−3)(u+1) becomes (q−2)(q+2) by substituting u=1+q, so it is symmetric with respect to q=0, that is, u=1. The residual F(u) which is the product of this function and the point symmetric function u(u−1)(u−2) with respect to the point u=1 is also point symmetric with respect to the point u=1, so it is evident that the integral from u=0 to u=2 is zero. The point u=3 is not used by Simpson's 1/3 rule but it is a mater of course that the residual becomes zero at the point because it is used in the proof of the rule. The residual becomes also zero at the point u=−1 symmetric with respect to u=1 which is the mid point of the integral range. However, it contradicts the supposition that the two points exist in the integral range. It shows that the integral using two interval has not the point q where F(q)=0 is satisfied except at the equidistant points in the integral range and by which the integral of the residual F(u) becomes zero. . .
The residual F(u) becomes zero at two points of u=3 and u=−1 together with the three equidistant points. The function (u−3)(u+1) becomes (q−2)(q+2) by substituting u=1+q, so it is symmetric with respect to q=0, that is, u=1. The residual F(u) which is the product of this function and the point symmetric function u(u−1)(u−2) with respect to the point u=1 is also point symmetric with respect to the point u=1, so it is evident that the integral from u=0 to u=2 is zero. The point u=3 is not used by Simpson's 1/3 rule but it is a mater of course that the residual becomes zero at the point because it is used in the proof of the rule. The residual becomes also zero at the point u=−1 symmetric with respect to u=1 which is the mid point of the integral range. However, it contradicts the supposition that the two points exist in the integral range. It shows that the integral using two interval has not the point q where F(q)=0 is satisfied except at the equidistant points in the integral range and by which the integral of the residual F(u) becomes zero.
. .
In usual, Simpson's 1/3 rule with remainder is proofed by use of the supposition that the integrand is expressed in Taylor's expansion of the third order with remainder. However, the function of the third order is not fixed by use of only three equidistant points. It is wrong to consider that there is no trouble because the term of the third order does not influence the result of integral. Above results show it. In practice, fixing the function of the third order by use of the fourth point u=3 implicitly, it integrates the two intervals of the three intervals, so it is the same as the integrand of Eq. (4.19) uses the fourth point. The integral of two intervals must be equal to the sum of the integral of every interval but usual remainder of Simpson's 1/3 rule is not equal to it. The integral of the first interval of the three intervals using four equidistant points is expressed as follows by use of p=4 and y'=f in Eq. (4.12).
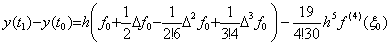 ____(4.21)
When the integrand is f(t)=t4, using the equidistant interval h=1, the constant Rq of remainder and the residual F(u) are obtained as follows and the residual F(u) is identical with zero because of Rq=1. ____(4.21)
When the integrand is f(t)=t4, using the equidistant interval h=1, the constant Rq of remainder and the residual F(u) are obtained as follows and the residual F(u) is identical with zero because of Rq=1.
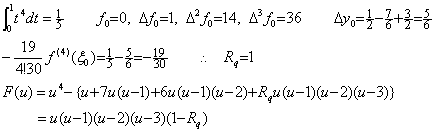 ____
In case of f(t)=t5, it is sure that the residual becomes F(u)=0 at u=0.447…, where is about mid point of the first interval because of Rq=5 as follows. ____
In case of f(t)=t5, it is sure that the residual becomes F(u)=0 at u=0.447…, where is about mid point of the first interval because of Rq=5 as follows.
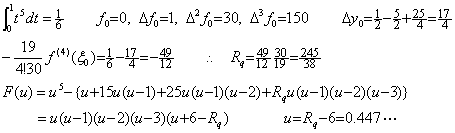 ____
The integral of the second interval of the three intervals is expressed in Eq. (4.22) by the first equation of Eq. (4.14). ____
The integral of the second interval of the three intervals is expressed in Eq. (4.22) by the first equation of Eq. (4.14).
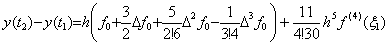 ____(4.22)
In case of f(t)=t4, the residual F(u) is identical with zero, because Rq=1 is obtained by the constant derivative f(4)(t)≡4!, without using the error of the approximate integral from the correct integral of this interval. In case of f(t)=t5, the constant Rq and the residual F(u) are as follows and it is sure that the residual becomes F(u)=0 at the mid point u=1.5 of the second interval. ____(4.22)
In case of f(t)=t4, the residual F(u) is identical with zero, because Rq=1 is obtained by the constant derivative f(4)(t)≡4!, without using the error of the approximate integral from the correct integral of this interval. In case of f(t)=t5, the constant Rq and the residual F(u) are as follows and it is sure that the residual becomes F(u)=0 at the mid point u=1.5 of the second interval.
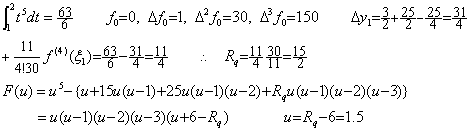 . .
The integral of two intervals is the sum of both integral. Adding Eq. (4.21) and Eq. (4.22), Simpson's 1/3 rule is obtained but the remainder is not equal to the remainder of Eq. (4.17). f(4)(ξ0) of the remainder in Eq. (4.21) is the value giving the remainder of the integrand f(t) at the point q=0.447…, where of the interval [0, 1] the residual is F(u)=0. f(4)(ξ1) of the remainder in Eq. (4.22) is the value giving the remainder of the integrand f(t) at the point q=1.5, where of the interval [1, 2] the residual is F(u)=0. Both are not equal in general. In such case that the integrand is y'(t)=f(t)=t4 so f(4)(t) is constant, both are equal and the remainder of Eq. (4.17) is satisfied. The usual remainder of Simpson's 1/3 rule is satisfied only in such case. However, more strictly speaking, the integral of two intervals must be obtained by using the integrand fixed in the two intervals and by adding the integral results of every interval, where it is certain that the integral of the residual F(u) becomes zero. Accordingly, Simpson's 1/3 rule must be obtained as follows. . .
The integral of two intervals is the sum of both integral. Adding Eq. (4.21) and Eq. (4.22), Simpson's 1/3 rule is obtained but the remainder is not equal to the remainder of Eq. (4.17). f(4)(ξ0) of the remainder in Eq. (4.21) is the value giving the remainder of the integrand f(t) at the point q=0.447…, where of the interval [0, 1] the residual is F(u)=0. f(4)(ξ1) of the remainder in Eq. (4.22) is the value giving the remainder of the integrand f(t) at the point q=1.5, where of the interval [1, 2] the residual is F(u)=0. Both are not equal in general. In such case that the integrand is y'(t)=f(t)=t4 so f(4)(t) is constant, both are equal and the remainder of Eq. (4.17) is satisfied. The usual remainder of Simpson's 1/3 rule is satisfied only in such case. However, more strictly speaking, the integral of two intervals must be obtained by using the integrand fixed in the two intervals and by adding the integral results of every interval, where it is certain that the integral of the residual F(u) becomes zero. Accordingly, Simpson's 1/3 rule must be obtained as follows.
. .
[Theorem 4.4] . . Simpson's 1/3 rule with remainder is,
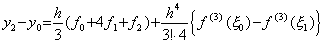 ____(4.23)
[Proof]. .Using p=3 for Eq.(4.12) and (4.14), ____(4.23)
[Proof]. .Using p=3 for Eq.(4.12) and (4.14),
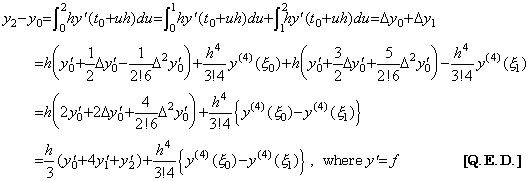
. .
In case of integrating the previous example in Eq. (4.18) from t=0 to t=1 by use of the above mentioned integral formula of the interval [0, 1] with the equidistant interval h=1, the remainder term and the residual F(u) become as follows and F(u) becomes zero at mid point u=1/2. It does not become zero at u=2, because the points such that F(u)=0 is satisfied are three points only in case that F(u) is the third order. However, it does not influence the integral of this interval.
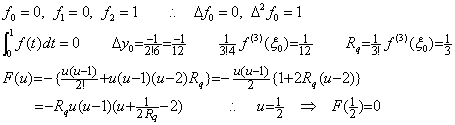 In case of integrating Eq. (4.18) from t=1 to t=2 by use of the above mentioned integral formula of the interval [1, 2], the remainder term and the residual F(u) become as follows and F(u) becomes zero at a point between u=1 and u=2. In this case, F(u) does not become zero at u=0. The cause is that the integrand is what connects distinct two functions at t=1 so smoothly that f(3)(t) is continuous. However, it does not influence the integral of this interval.
In case of integrating Eq. (4.18) from t=1 to t=2 by use of the above mentioned integral formula of the interval [1, 2], the remainder term and the residual F(u) become as follows and F(u) becomes zero at a point between u=1 and u=2. In this case, F(u) does not become zero at u=0. The cause is that the integrand is what connects distinct two functions at t=1 so smoothly that f(3)(t) is continuous. However, it does not influence the integral of this interval.
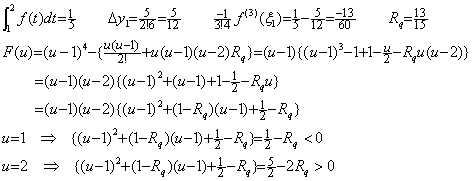 The integral from t=0 to t=2 is the sum of both and the remainder term of Theorem 4.4 gives the correct remainder of Simpson's 1/3 rule as follows.
The integral from t=0 to t=2 is the sum of both and the remainder term of Theorem 4.4 gives the correct remainder of Simpson's 1/3 rule as follows.
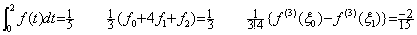 In order that the residual F(u) becomes zero at a point between every interval together with u=0, 1, 2, the integrand f(t) must be one and the same over this two intervals and f(3)(t) must be more once continuous differentiable. If the integrand is f(t)=(t−1)4 in case of t<1 too, this condition is satisfied and the residual becomes zero at u=7/15 for the integral of the interval [0, 1] or at u=23/15 for the integral of the interval [1, 2] as follows.
In order that the residual F(u) becomes zero at a point between every interval together with u=0, 1, 2, the integrand f(t) must be one and the same over this two intervals and f(3)(t) must be more once continuous differentiable. If the integrand is f(t)=(t−1)4 in case of t<1 too, this condition is satisfied and the residual becomes zero at u=7/15 for the integral of the interval [0, 1] or at u=23/15 for the integral of the interval [1, 2] as follows.
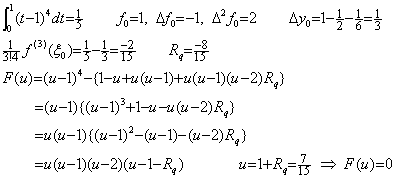
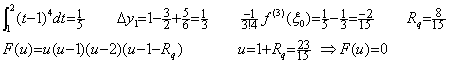 The integral of the twice interval [0, 2] is the sum of above integrals and the value of remainder is equal to the error of Simpson's 1/3 rule without remainder term as follows.
The integral of the twice interval [0, 2] is the sum of above integrals and the value of remainder is equal to the error of Simpson's 1/3 rule without remainder term as follows.
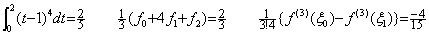 In this case, applying the mean value theorem to the difference of the two remainders because f(3)(t) is differentiable, the result is equivalent to the remainder of Eq. (4.17). However, it is wrong to consider that Simpson's 1/3 rule has the precision corresponding to f(4)(ξ), that is, approximation by the function of the third order.
In this case, applying the mean value theorem to the difference of the two remainders because f(3)(t) is differentiable, the result is equivalent to the remainder of Eq. (4.17). However, it is wrong to consider that Simpson's 1/3 rule has the precision corresponding to f(4)(ξ), that is, approximation by the function of the third order.
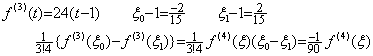 . .If the function f(t) is at3+bt2+ct+d, the integral from t0 to t2 is obtained correctly by Simpson's 1/3 rule because f(3)(t)=3!a, but the first term at3 has no effect on the integral because the integral from t0 to t2 of a(t−t0)(t−t1)(t−t2) is zero. Furthermore, even if the integrand is added k(t−t0)(t−t1)(t−t2) with arbitrary coefficient k, the addend has no influence on the integral. However, the function is very different from f(t) and the integral of one interval, that is, from t0 to t1 or from t1 to t2, is also very different from that of f(t). The cause is that the function of the third order is indefinite in case of using only three equidistant points. . .If the function f(t) is at3+bt2+ct+d, the integral from t0 to t2 is obtained correctly by Simpson's 1/3 rule because f(3)(t)=3!a, but the first term at3 has no effect on the integral because the integral from t0 to t2 of a(t−t0)(t−t1)(t−t2) is zero. Furthermore, even if the integrand is added k(t−t0)(t−t1)(t−t2) with arbitrary coefficient k, the addend has no influence on the integral. However, the function is very different from f(t) and the integral of one interval, that is, from t0 to t1 or from t1 to t2, is also very different from that of f(t). The cause is that the function of the third order is indefinite in case of using only three equidistant points.
. .
It also comes to the same thing in case that any function f(t) is approximated by the function of the third order. The solution of the trouble requires the equidistant point t3=t2+h. In the case, from the second formula of Eq.(4.14),
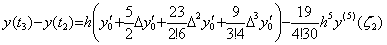 _____(4.24)
Accordingly, by Eq.(4.21) Eq.(4.22) and Eq.(4.24), the integral of the three intervals [t0, t3] becomes as follows. _____(4.24)
Accordingly, by Eq.(4.21) Eq.(4.22) and Eq.(4.24), the integral of the three intervals [t0, t3] becomes as follows.
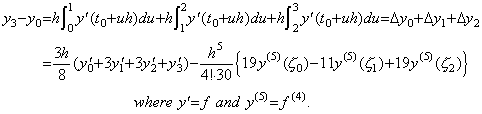 ___(4.25)
. .This is the integral which uses the integrand approximated by the function of the third order. It seems that the remainder is greater than the remainder of Simpson's 1/3 rule obtained by adding Eq. (4.21) and Eq.(4.22). However, the comparison is not correct because this obtains the integral of three equidistant intervals, while Simpson's 1/3 rule obtains the integral of two equidistant intervals, approximating the integrand by use of three equidistant intervals. The comparison must be drawn in case of the same integral range by use of the equidistant interval equal to 2h/3, where h is the equidistant interval of Simpson's 1/3 rule. ___(4.25)
. .This is the integral which uses the integrand approximated by the function of the third order. It seems that the remainder is greater than the remainder of Simpson's 1/3 rule obtained by adding Eq. (4.21) and Eq.(4.22). However, the comparison is not correct because this obtains the integral of three equidistant intervals, while Simpson's 1/3 rule obtains the integral of two equidistant intervals, approximating the integrand by use of three equidistant intervals. The comparison must be drawn in case of the same integral range by use of the equidistant interval equal to 2h/3, where h is the equidistant interval of Simpson's 1/3 rule.
4.4 The integral operator.
. .
Comparing Theorem 4.3 with Theorem 3.7, it is found that the relation between the coefficients of the integral formulas in Eqs.(4.12) and (4.14) is of the same as the relation between the coefficients of the differential formulas in Eq.(3.33). The proof of Theorem 3.10 only uses the property which is independent of the actual values except the coefficients must satisfy the relation described in Theorem 3.7. Accordingly, obtaining the successive differences of the integral formulas in Eqs.(4.12) and (4.14), those have the same relation as the relation between the first formula of Eq.(3.33) and the successive differences in Theorem 3.10. . .
[Theorem 4.5]. .Supposing ak is expressed in Eq.(4.11) and denoting the remainders of Eqs.(4.12) and (4.14) by AmRem, for 0≤m≤p−1,
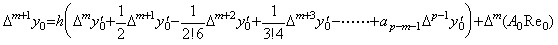 ____(4.26) ____(4.26)
| for m=p, |
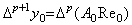 |
(4.27) |
[Proof]. .Expressing every equation of Eqs.(4.12) and (4.14) in general form,
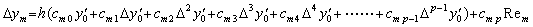 where there exist the equality c0k=ak and the following relation by Theorem 4.3.
where there exist the equality c0k=ak and the following relation by Theorem 4.3.
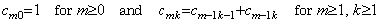 The (m+1)th difference Δm+1y0 is obtained by calculating the m-th differences by respective terms in the right sides of the equations expressed in general form. It results to calculating the m-th differences of the coefficients of respective terms except the remainder term is denoted as Δm(A0Re0) because of Am=cmp.
The (m+1)th difference Δm+1y0 is obtained by calculating the m-th differences by respective terms in the right sides of the equations expressed in general form. It results to calculating the m-th differences of the coefficients of respective terms except the remainder term is denoted as Δm(A0Re0) because of Am=cmp.
| 1) | . .If m=0, Eq.(4.26) is of the same as Eq.(4.12). |
| 2) | . .If m=1, the first term with y0' vanishes from the second difference Δ2y0=Δy1−Δy0 because the coefficient is Δc00=c10−c00=1−1=0. The coefficient of every term with k≥1 comes to the coefficient of the term with k−1 in the case m=0, because it is Δc0k=c1k−c0k=c0k−1. Hence,
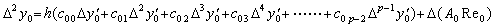 |
| 3) | . .If m=2, the first term with y0' vanishes from the third difference Δ3y0=Δy2−2Δy1+Δy0 because the coefficient is Δ2c00=c20−2c10+c00=1−2+1=0. The second term with Δy0' also vanishes because the coefficient is,
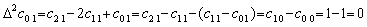
The coefficient of every term with k≥2 comes to the coefficient of the term with k−1 in the case m=1, because of
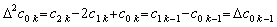 Hence,
Hence,
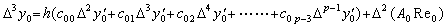 |
| 4) | . .Supposing Eq.(4.26) is held for m=n, the coefficients are zero up to the term with Δn−1y0'. Hence,
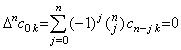 . .(k<n),______ . .(k<n),______
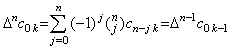 . .(k≥n), . .(k≥n),
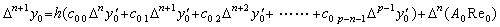 Accordingly if m=n+1,
Accordingly if m=n+1,
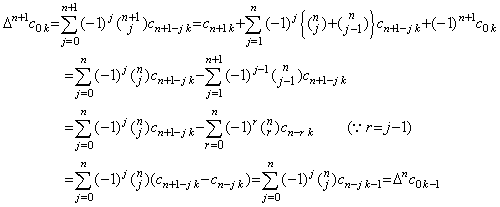 where Δn+1c0k=0 if k≤n because Δnc0k−1=0 for k−1<n by the supposition. Therefore,
where Δn+1c0k=0 if k≤n because Δnc0k−1=0 for k−1<n by the supposition. Therefore,
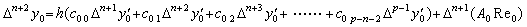 |
| 5) | . .In above case, the integer k must be 0≤k≤p−1. Hence if n+1=p, the above equation comes to Δp+1y0=Δp(A0Re0) because all the terms except of the remainder have vanished by the reason that the suffix of the coefficient is p−n−2<0. |
| [Q.E.D.] |
. .By Theorem 4.5, the integral of the derivative y' (t) expressed in Eq.(4.8) is expressed in following matrix equation. The element Δp+1y0 may not appear on the left side because it is independent of the integrand Y0' and only depends on the element Δp(A0Re0) of the remainder.
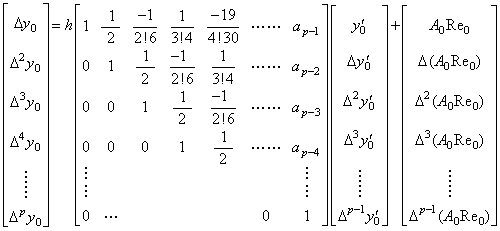 ___(4.28) ___(4.28)
. .
[Theorem 4.6]. .For the integer k such that 0≤k≤p,
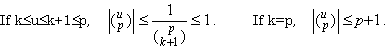 ____(4.29)
[Proof]. .If 0≤k≤p−1, there are following relations. ____(4.29)
[Proof]. .If 0≤k≤p−1, there are following relations.
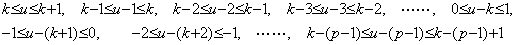 Accordingly, if j≤k, the maximum values of |u−j| are the upper limits and if j≥k+1, they are the absolute values of the lower limits. Hence,
Accordingly, if j≤k, the maximum values of |u−j| are the upper limits and if j≥k+1, they are the absolute values of the lower limits. Hence,
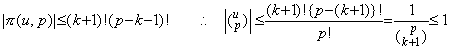 If k=p, because the last (u−j) is 1≤u−p+1≤2 and all are positive,
If k=p, because the last (u−j) is 1≤u−p+1≤2 and all are positive,
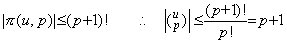 ______[Q.E.D.] ______[Q.E.D.]
. .By Theorem 4.6,
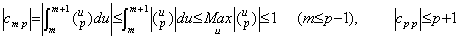 ___(4.30). .
The remainder in Eq.(4.28) is the vector of the product of the two functions which have the following values Am and Rem respectively for u=m. ___(4.30). .
The remainder in Eq.(4.28) is the vector of the product of the two functions which have the following values Am and Rem respectively for u=m.
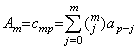 _________ _________
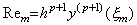 Hence it may be expressed in the product of the two vectors which are the vectors of respective functions. The successive differences of the values Am are ap−m obviously. Accordingly, the two vectors are,
Hence it may be expressed in the product of the two vectors which are the vectors of respective functions. The successive differences of the values Am are ap−m obviously. Accordingly, the two vectors are,
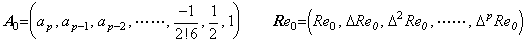 The remainder is expressed in R0=A0×Re0, where the last elements of the both vectors are omitted in Eq.(4.28). Because the matrix into which the vector A0 is expanded has cmp in the principal diagonal and that of the vector Re0 has Rem there, by Eq.(4.30),
The remainder is expressed in R0=A0×Re0, where the last elements of the both vectors are omitted in Eq.(4.28). Because the matrix into which the vector A0 is expanded has cmp in the principal diagonal and that of the vector Re0 has Rem there, by Eq.(4.30),
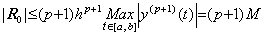 The conditions R0→0 and then Δp+1y0→0 are satisfied because there exists the condition M=0 or h→0, when the integrand y' (t) is expressed in the vector Y0'. Hence denoting the matrix of Eq.(4.28) by D−1, the matrix equation comes to,
The conditions R0→0 and then Δp+1y0→0 are satisfied because there exists the condition M=0 or h→0, when the integrand y' (t) is expressed in the vector Y0'. Hence denoting the matrix of Eq.(4.28) by D−1, the matrix equation comes to,
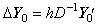 ________(4.31)
. .
The left side ΔY0 is equal to the difference Y1−Y0, that is, it expresses Δy(t)=y(t+h)−y(t). Accordingly, Eq.(4.28) and Eq.(4.31) express the difference of the integral expressed in Eq.(4.1). It is, ________(4.31)
. .
The left side ΔY0 is equal to the difference Y1−Y0, that is, it expresses Δy(t)=y(t+h)−y(t). Accordingly, Eq.(4.28) and Eq.(4.31) express the difference of the integral expressed in Eq.(4.1). It is,
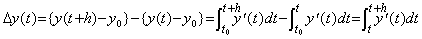 _____(4.32)
Hence the operator hD−1 denotes the integral of the interval h from any point t of the integrand y' (t). Because of (Δ+1)y(t)=y(t+h), _____(4.32)
Hence the operator hD−1 denotes the integral of the interval h from any point t of the integrand y' (t). Because of (Δ+1)y(t)=y(t+h),
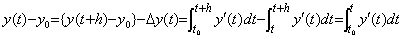 _____(4.33)
This equation is equivalent to Eq.(4.1) and is expressed in matrix equation by use of the operator ΔT and Eq.(4.31) as follows. _____(4.33)
This equation is equivalent to Eq.(4.1) and is expressed in matrix equation by use of the operator ΔT and Eq.(4.31) as follows.
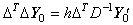 _______(4.34)
The operator ΔT shifts the elements of the vector ΔY0 and the matrix D−1 down by one cell and changes the first elements of the vector and columns of the matrix to zero. The last term of Eq.(4.33) shows that the last elements of the vector and columns are removed. The meaning will be mentioned in Section 4.5. _______(4.34)
The operator ΔT shifts the elements of the vector ΔY0 and the matrix D−1 down by one cell and changes the first elements of the vector and columns of the matrix to zero. The last term of Eq.(4.33) shows that the last elements of the vector and columns are removed. The meaning will be mentioned in Section 4.5.
. .
Accordingly, Eq.(4.34) has no difference from Eq.(4.31) except the value zero of Eq.(4.1) at t=t0 is the result of the integral operation. The author's operational calculus does not treat it as the result of the integral operation and treats Eq.(4.34) as a part of the operation obtaining the vector Y0 as follows.
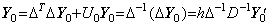 ________(4.35)
where U0 is the matrix unit which has the value 1 in the first row first column. Hence the author simply describes the operational expression of Eq.(4.1) as Eq.(4.31), because there is no confusion in the usual case. ________(4.35)
where U0 is the matrix unit which has the value 1 in the first row first column. Hence the author simply describes the operational expression of Eq.(4.1) as Eq.(4.31), because there is no confusion in the usual case.
. .
Because Eq.(4.35) adds the initial value y(t0) to the integral of the derivative y' (t), it gives the solution of the differential equation. Substituting Eq.(3.40) into Eq.(4.35),
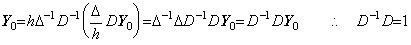 ______(4.36)
Hence the author defines h(ΔD)−1 as the integral operator, which is the inverse operator of the differential operator Δh−1D. Eq.(4.36) is held independently of the remainder approaching to zero as follows, if the order of both matrix is equal. ______(4.36)
Hence the author defines h(ΔD)−1 as the integral operator, which is the inverse operator of the differential operator Δh−1D. Eq.(4.36) is held independently of the remainder approaching to zero as follows, if the order of both matrix is equal.. .
[Theorem 4.7]. .D−1D=1 is always held for any order of the matrices.
[Proof]. .1). .If the matrices are of order 1, it is evidently held.
| 2) | . .If the matrices are of order 2,
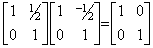 |
| 3) | . .Supposing it is held when the matrices are of order n, it is also held when the matrices are of order n+1 as follows. Denoting the elements of the first row of D−1 and D by ak and dk respectively, what should be shown is the proof of,
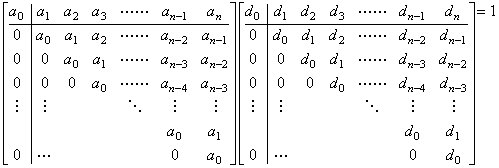 . .Let us denote the i-th row of the left matrix by Ai and the j-th column of the right matrix by Dj. In case of i≥2, the products of Ai and D1 are all zero because the first elements of Ai are all zero and the products of Ai and Dj with j≥2 come to the product of the submatrices of order n separated by the two lines. The product is the unit submatrix by the supposition. In case of i=1, the product of A1 and D1 is one but the products of A1 and Dj with 2≤j≤n are all zero, because the products are equivalent to the products of the first row of the left submatrix of order n and the right submatrix of order n by the reason that the last elements of Dj with j≤n are all zero. Therefore the proof is completed by showing the product of A1 and Dn+1 comes to zero. Denoting it by s,
. .Let us denote the i-th row of the left matrix by Ai and the j-th column of the right matrix by Dj. In case of i≥2, the products of Ai and D1 are all zero because the first elements of Ai are all zero and the products of Ai and Dj with j≥2 come to the product of the submatrices of order n separated by the two lines. The product is the unit submatrix by the supposition. In case of i=1, the product of A1 and D1 is one but the products of A1 and Dj with 2≤j≤n are all zero, because the products are equivalent to the products of the first row of the left submatrix of order n and the right submatrix of order n by the reason that the last elements of Dj with j≤n are all zero. Therefore the proof is completed by showing the product of A1 and Dn+1 comes to zero. Denoting it by s,
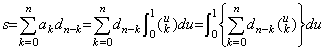 ______(4.37)
. .Supposing, ______(4.37)
. .Supposing,
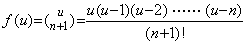 it is able to express the function in Newton's interpolation formula with p=n+1 and with the remainder, which is zero because of f(n+2)(u)≡0. Supposing equidistant points are u=0, 1, 2, ………, n+1 with the interval h=1, the successive differences are Δkf0=0 for k≤n and Δn+1f0=1 because of f0=f1=f2= ………=fn=0 and fn+1=1. Hence the interpolation formula is also expressed in f(u). The derivative of Newton's interpolation formula has no remainder for any point in case of
it is able to express the function in Newton's interpolation formula with p=n+1 and with the remainder, which is zero because of f(n+2)(u)≡0. Supposing equidistant points are u=0, 1, 2, ………, n+1 with the interval h=1, the successive differences are Δkf0=0 for k≤n and Δn+1f0=1 because of f0=f1=f2= ………=fn=0 and fn+1=1. Hence the interpolation formula is also expressed in f(u). The derivative of Newton's interpolation formula has no remainder for any point in case of
f(n+2)(u)≡0. By Eq.(3.29),
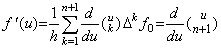 The author's operational calculus expresses the derivative in the matrix equation with the remainder, which is identical with zero.
The author's operational calculus expresses the derivative in the matrix equation with the remainder, which is identical with zero.
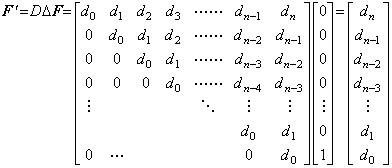 Accordingly, the derivative f ' (u) may be expressed in Newton's interpolation formula by using the components of the vector F'. It comes to the integrand of Eq.(4.37). Therefor the integral is,
Accordingly, the derivative f ' (u) may be expressed in Newton's interpolation formula by using the components of the vector F'. It comes to the integrand of Eq.(4.37). Therefor the integral is,
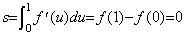 ________[Q.E.D.] ________[Q.E.D.] |
. .
The integral operator has the operator Δ−1, which is the inverse operator of the operator Δ but not the inverse matrix of the matrix Δ because there does not exists the inverse matrix by det(Δ)=0. It was defined in the matrix equation Δ−1Δ=ΔTΔ+U0=1 in Section 2.4. Accordingly, the integral operator must operate the initial value y0 by the equation after ΔY0 has been obtained by Eq.(4.31).. .
[Theorem 4.8]. .Denoting the elements standing in the first row and (k+1)th column of the matrix D and D−1 by dk and dk−1 respectively for k≥0,
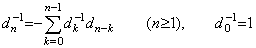 ______(4.38)
[Proof]. .Because the value s in Eq.(4.37) is zero for n≥1, ______(4.38)
[Proof]. .Because the value s in Eq.(4.37) is zero for n≥1,
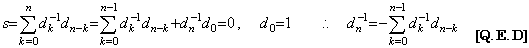
. .
The element standing in the first row and (k+1)th column of the matrix D is easily obtained by (−1)k/(k+1) for k≥0. Accordingly, the element standing in the first row and (n+1)th column of the matrix D−1 is successively obtained for n≥0 by Theorem 4.8 without using Stirling's numbers.
To 4.5 The predictor and corrector.
|
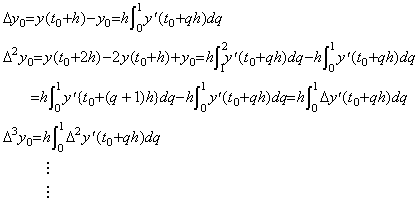
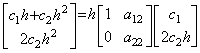
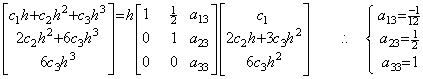
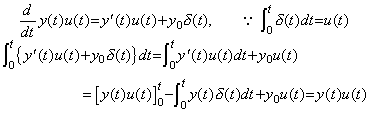
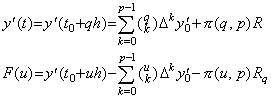
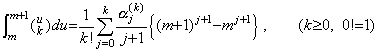 ____(4.10)
____(4.10)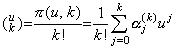 ______and______
______and______
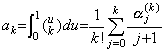 ______(4.11)
______(4.11)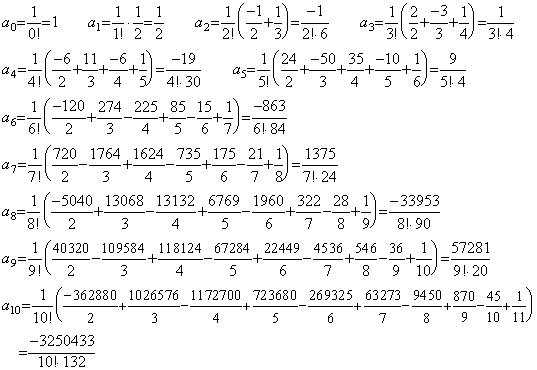
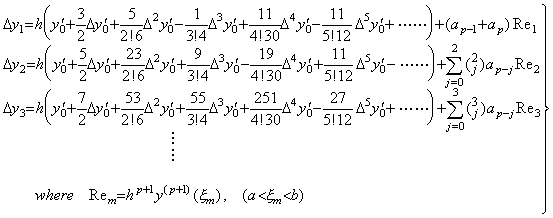 (4.14)
(4.14)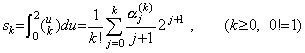
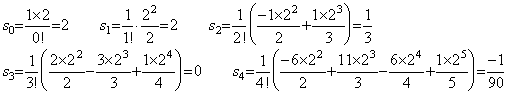
 . .
The residual F(u) has the zero value for u=q and increases in the absolute value by increasing in |u−q|, because the constant Rq increases in the difference from the R value for any u. However it comes to zero at the equidistant points because of multiplying the difference by
. .
The residual F(u) has the zero value for u=q and increases in the absolute value by increasing in |u−q|, because the constant Rq increases in the difference from the R value for any u. However it comes to zero at the equidistant points because of multiplying the difference by 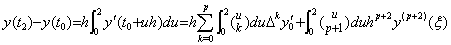 ____(4.19)
____(4.19)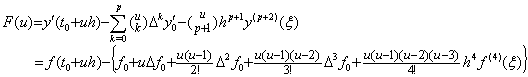 ___(4.20)
___(4.20)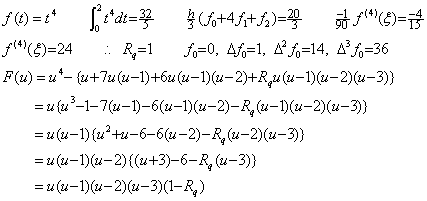
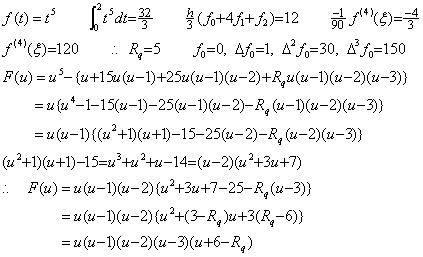
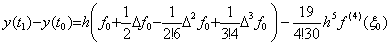 ____(4.21)
____(4.21)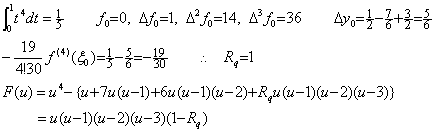 ____
____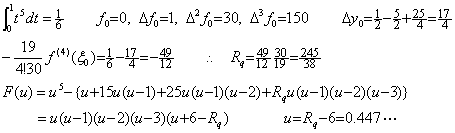 ____
____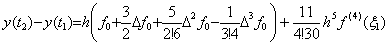 ____(4.22)
____(4.22)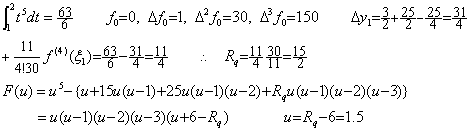
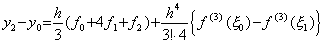 ____(4.23)
____(4.23)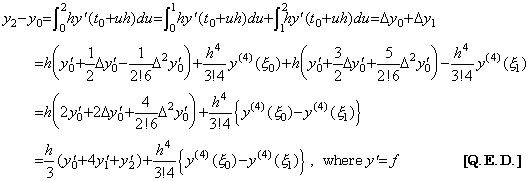
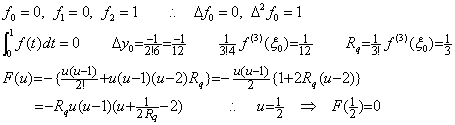
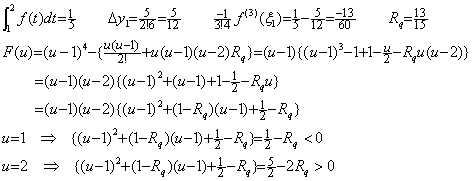
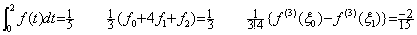
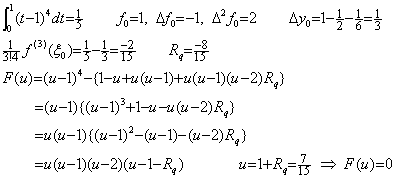
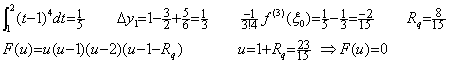
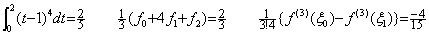
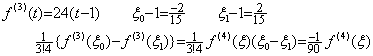
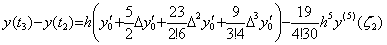 _____(4.24)
_____(4.24)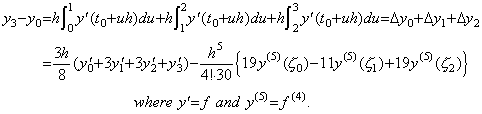 ___(4.25)
___(4.25)![]() ____(4.26)
____(4.26)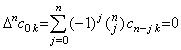 . .(k<n),______
. .(k<n),______
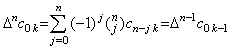 . .(k≥n),
. .(k≥n),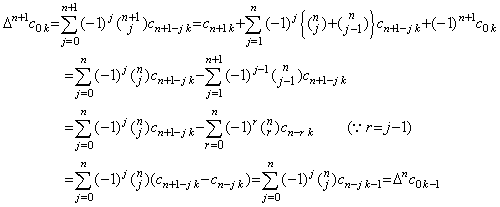
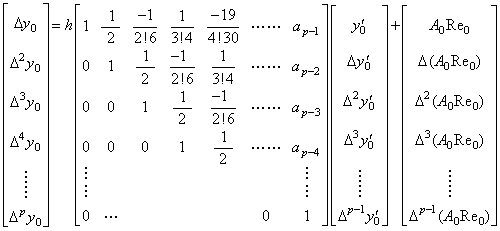 ___(4.28)
___(4.28)
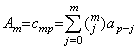 _________
_________
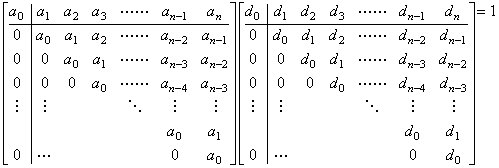
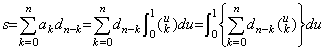 ______(4.37)
______(4.37)