. . The integral operator obtains the solution of differential equations and the operation is expressed in Eq.(4.35). It must be carried out by use of Eq.(4.31) except for the initial value. If the integrand Y0' consists of the p values of y0' to yp−1', the result ΔY0 consists of the p+1 values of y0 to yp as expressed in Eq.(4.28). Accordingly, the value yp' at the last point tp has no effect on the result. By the reason, if the integrand is the function of order p−1, the result comes to the function of order p with no remainder. However, if the integrand is any continuous function, the result with effect of yp' will have better accuracy than the result without use of yp', because the integrand is of higher order.
. . The author names the integral operator multiplied by Δ, that is, hD−1 in Eq.(4.28) as the predictor by the reason that it obtains the integral from t0 to tp by use of the integrand from t0 to tp−1. The usual predictors are obtained by expressing yp in y0', y1', ………, yp−1' for successive p values as follows.
. . When the matrix D−1 is of order one, that is p=1, it is Euler's rule because the matrix equation is equivalent to
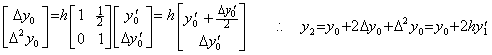
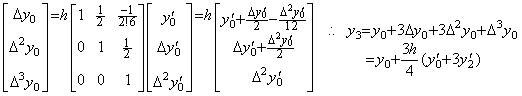
hD−1 as the corrector when the matrix D−1 has all zero elements in the last row. Accordingly, the corrector for the predictor of order p is the submatrix of the matrix of order p+1 and is expressed in the rectangular matrix of order (p×(p+1)). The usual correctors are obtained by expressing yp in y0', y1', ………, yp−1' and yp' for successive p values as follows.
. . When the matrix D−1 is of order (1×2), it is the corrector for Euler's rule and is the trapezoidal rule because of,
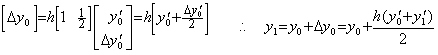
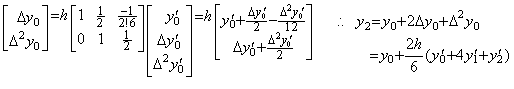
. . When the matrix D−1 is of order (3×4), it is Simpson's 3/8 rule, that is,
. . Printing out Milne's solutions of the differential equation y' =−ty by every iteration, we shall find that they approach the accurate solutions by once or twice iterations around t=0 but they does not approach the accurate solutions around t=5 even if the corrector is iterated many times. The cause is that it is sufficient to use Simpson's 1/3 rule as corrector around t=0 but it is not sufficient around t=5. It has no effect to use Milne's predictor, because it is sufficient to use the midpoint rule as mentioned in Chapter 2 Section 1 and 2.
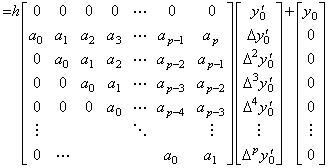
. . In Eq.(4.31), the vector ΔY0 and Y0' have the equal number of components because the operator is the square matrix of order p. The corrector must append the last component Δpy0' to the vector Y0', because it must obtain the integral from t0 to tp by use of the integrand from t0 to tp. In the case, the operator becomes the matrix of order p+1 and the vector ΔY0 has the last component Δp+1y0. It is removed by premultiplying ΔY0 by ΔT and the vector ΔTΔY0 has the initial value zero as the first element. This operation means subtracting the integral of t to t+h of y' (t) from the integral of t0 to t+h of y' (t) as expressed in Eq.(4.33) and the matrix equation is expressed in Eq.(4.34). Adding the initial value y0 to the both sides of Eq.(4.33), the solution y(t) is obtained. It is expressed in Eq.(4.35) and also expressed in following equation.
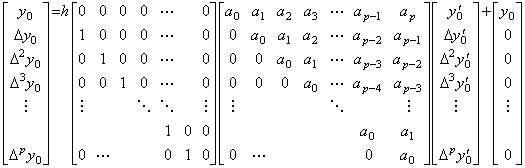
 ____(4.40)
____(4.40). . The integral operator h(ΔD)−1 in Eq.(4.35) is the corrector rigorously speaking, because it obtains the integral from t0 to tp by use of the integrand from t0 to tp as shown in the detailed expression of Eq.(4.39). However, supposing the last component Δpy0' is zero when it is unknown, the operator obtains the integral from t0 to tp by use of the integrand from t0 to tp−1 and the supposition means the prediction. Hence the author usually uses both of Eq.(4.31) and (4.35) without distinction between the predictor and the corrector.
. . When we will obtain the integral of a given function, it is better to use the corrector of order (p×(p+1)) because it usually gives more precise results than the predictor of order p. When we will obtain the solution of a given differential equation, it is able to use a pair of the predictor and corrector as follows.
. . We first obtain y0' by the given initial value y0, which is the only starting value required in case of this calculus. Then we obtain the required precise p solutions by successive use of the predictor of order 1, the corrector of order (1×2), the predictor of order 2, the corrector of order (2×3), ………, the predictor of order p and the corrector of order (p×(p+1)). All the correctors except the last corrector may be omitted because the predictor of order k includes the corrector of order ((k−1)×k).
. . The last corrector must not be repeated many times by use of a constant p, because it has no effect on obtaining more precise result except of twice or three times repeats and has the cause of the unstable result as the usual predictor-corrector methods.
4.6 The double integral operator.
. .
The derivative y' (t) is obtained by the differentiation of y(t)−y0 and the second derivative y"(t) is obtained by the differentiation of y' (t)−y0'. Hence,
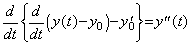 ____(4.42)
____(4.42)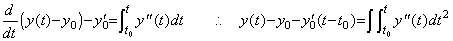 ___(4.43)
___(4.43)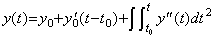 _____(4.44)
_____(4.44). .
[Theorem 4.9]. .Eliminating y0 and y0' from Eq.(4.43),
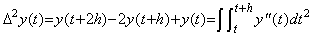 _____(4.45)
_____(4.45)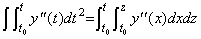
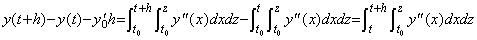
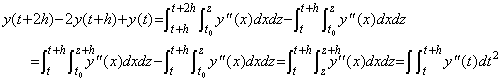
| [Q.E.D.] |
Appendix
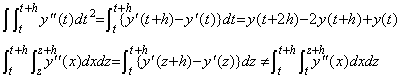
. . [Theorem 4.10]. .When m≥0, the double integral from t to t+h of Δmy"(t) is,
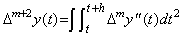 _____(4.46)
_____(4.46)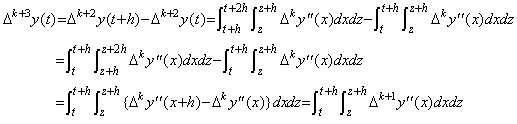
| [Q.E.D.] |
Appendix
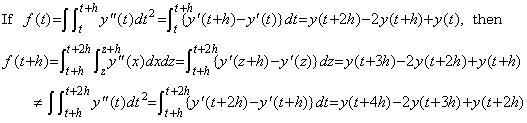
. . [Theorem 4.11]. .Supposing y(t)∈Cp+1[a, b] and 1≤m≤p+1, there exists a value ξ such that,
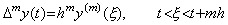 ______(4.47)
______(4.47)| 1). . | if m=1,. .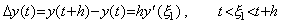 |
| 2) | if m=2,. .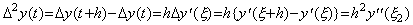 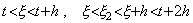 |
| 3) | Supposing the theorem is held for m=n, if m=n+1,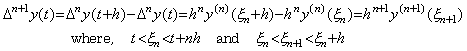 . .[Q.E.D.] . .[Q.E.D.] |
. . [Theorem 4.12]. .Supposing y(t)∈Cp+1[a, b], Δmy(t) is expressed in Eq.(4.48) for the real number r such that t=t0+rh∈[a, b].
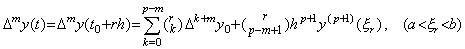 ___(4.48)
___(4.48)| 1) | . .If m=0, Eq.(4.48) is Newton's interpolation formula of y(t) shown in Theorem 3.1. |
| 2) | . .If m=1, it is the difference of the formula as shown in Theorem 3.3. The number of the equidistant points at which the remainder vanishes is decreased to the p points of r=0 to p−1, while Δy(t)∈Cp+1[a, b]. |
| 3) | . .If it is held for m=n, by Theorem 4.11 there exist a value ξ such that,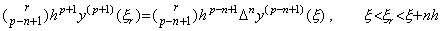 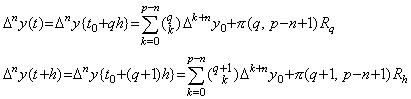 . . Considering the function F(u) as the residual of the function Δny(t0+uh) and its approximate formula with the constant Rq, the function G(u) or F(u+1) is the residual of the function Δny{t0+(u+1)h} and its approximate formula with the constant Rq instead of Rh. Using that G(u)−F(u) vanishes at the p−n+1 points of u=0 to p−n−1 and r, the following result is obtained in a similar way as the proof of Theorem 3.3. 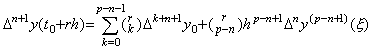 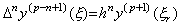 .. .[Q.E.D.] .. .[Q.E.D.]
|
. . The step 3 of the above proof may be shown by immediately using Eq.(4.48) substituted the value n for m as follows.
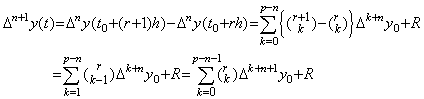
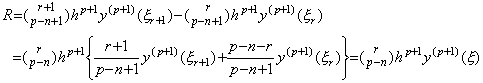
. . The inverse operation of the second differentiation is expressed in Eq.(4.43). When we express it in the matrix equation, we must obtain the successive differences of the left side. If t=t0, the left side comes to y(t)−y0−y0' (t−t0)=0 but it is not the result of the double integral. If t=t0+h, it is the result of the double integral but the difference of the two values of the left side has the value independent of the double integral and is not the component of the vector Y0, because it is expressed in Δy0−
. .
[Theorem 4.13]. .When y"(t)∈Cp−1[a, b], expressing it in Newton's interpolation formula, the successive differences of the results of the double integral is,
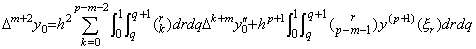 ___(4.49)
___(4.49)[Proof]. .The relation between y(t) and y"(t) is expressed in Eq.(4.46). Substituting t=t0 into it, Δm+2y0 is obtained.
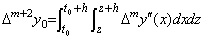
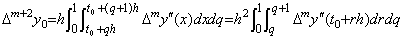 ____(4.50)
____(4.50)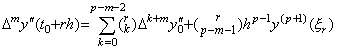
| [Q.E.D.] |
. . [Theorem 4.14]. .Denoting the double integral in the coefficient of Δk+my0" of Eq.(4.49) by ak2,
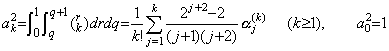 ____(4.51)
____(4.51)[Proof]. .Using Stirling's numbers,
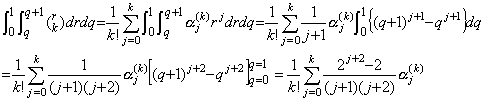
| [Q.E.D.] |
. . Using Stirling's numbers in Table 3.3, the values of Eq.(4.51) are obtained for k=0 to 10 as follows.
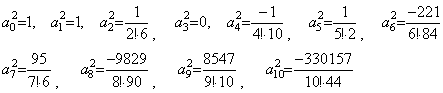
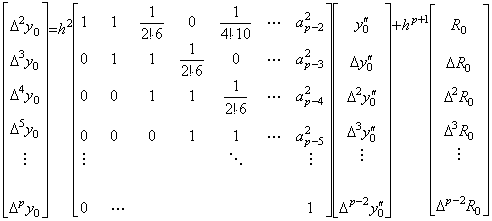 __(4.52)
__(4.52)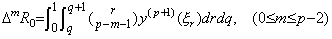
. . When the m value is m=p−1, Eq.(4.49) becomes the remainder only.
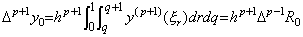 _____(4.53)
_____(4.53)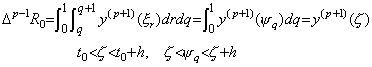
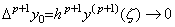
Accordingly, it is not expressed in the matrix equation (4.52).
. .
[Theorem 4.15]. .If h→0, the remainder of Eq.(4.52) is hp+1R→0.
[Proof]. .The diagonal elements hp+1Rm of the matrix into which the vector hp+1R is expanded are equivalent to the remainder at t=t0+mh of the equation which expresses the integrand of Eq.(4.45) in Newton's interpolation formula. Changing the integral variables x, z of Eq.(4.45) into r, q such that x=t0+rh and z=t0+qh.
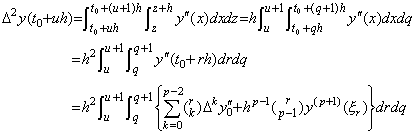
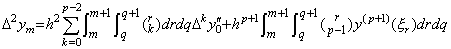 ___(4.54)
___(4.54)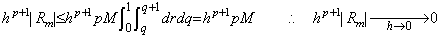
| [Q.E.D.] |
. .
Accordingly, denoting the matrix of Eq.(4.52) by D−2, the double integral is expressed in,
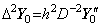 _______(4.55)
_______(4.55)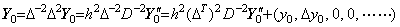 ___(4.56)
___(4.56). . The initial value y0' is expressed in the first row of the matrix equation of the differentiation Y0' =h−1DΔY0, that is,
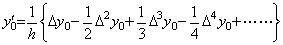 _____(4.57)
_____(4.57). . The matrix equation (4.55) obtains the results from t0 to tp by integrating the integrand from t0 to tp−2 as shown in Eq.(4.52). Hence the operator h2D−2 is the predictor which is the matrix of order p−1 and predicts the two interval from tp−2 to tp. On the other hand, the matrix equation (4.56) obtains the results from t0 to tp by integrating the integrand from t0 to tp, if the integrand may be expressed in the vector with the p+1 components of y0" to Δpy0". The matrix (ΔT)2D−2 is the matrix whose first and second rows have all zero and whose third to (p+1)th rows are of the same as the first to (p−1)th rows of the matrix D−2 of order p+1. Premultiplying the equation (4.56) by Δ2,
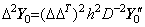 _______(4.58)
_______(4.58). .
[Theorem 4.16]. .The following is always held independently on the remainder.
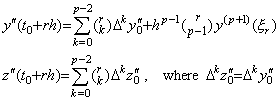
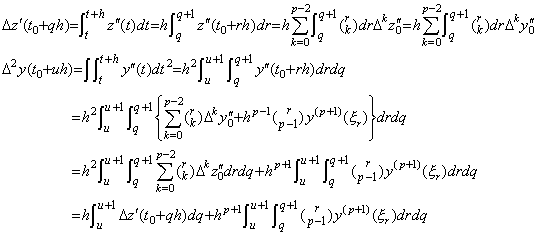
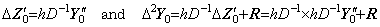
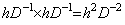 _____________[Q.E.D.]
_____________[Q.E.D.]. . Accordingly, the double integral by h2D−2 is equivalent to the twice integrals by hD−1. In the latter case, it is able to use the program of the single integral twice and it is not required to transform the initial value y0' to the difference Δy0 by Eq.(4.57) because the difference Δy0 is obtained by the second integral expressed in ΔY0=hD−1Y0', using the initial value y0'. However, it requires the twice calculating times of the former case and there may be the case in which some accuracy of results will be lost by the cause that Theorem 4.16 is not held accurately by the truncation errors of the elements of D−1.
4.7 The n multiple integral operator.
. .
The derivative y' (t) is obtained by the differentiation of y(t)−y0 and the second derivative y"(t) is obtained by the differentiation of y' (t)−y0'. In a similar way, the n-th derivative is obtained by the differentiation of y(n−1)(t)−y0(n−1). Hence,
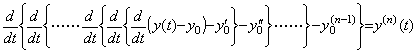 ___(4.60)
___(4.60)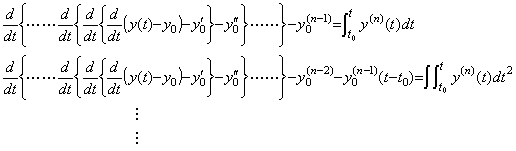
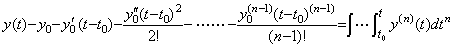 ____(4.61)
____(4.61)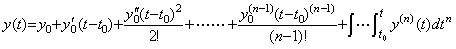 ___(4.62)
___(4.62)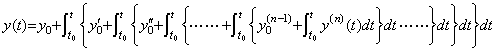 ___(4.63)
___(4.63)
. .
[Theorem 4.17]. .If y(t)∈Cp[a, b], there exists a value ξ such that,
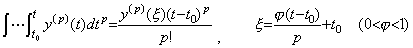 _____(4.64)
_____(4.64)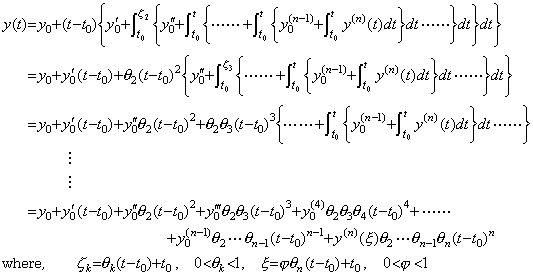
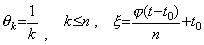
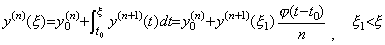
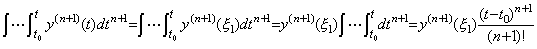
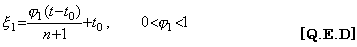
. . In order to introduce the n multiple integral operator, Eq.(4.61) is first expressed in the matrix equation using the successive differences of y(t) and y(n)(t). Accordingly, the initial values must be all eliminated from the equation because these are not the components of the both vectors of y(t) and y(n)(t).
. .
[Theorem 4.18]. .Eliminating all the initial values from Eq.(4.61),
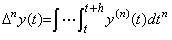 ________(4.65)
________(4.65)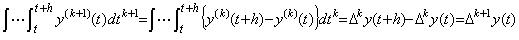
| [Q.E.D.] |
. . [Theorem 4.19]. .If the integer m is m≥0, Δm+ny(t) is,
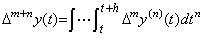 ________(4.66)
________(4.66)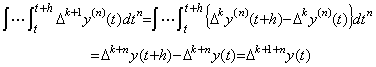
| [Q.E.D.] |
. . [Theorem 4.20]. .When y(n)(t)∈Cp−n+1[a, b], expressing it in Newton's interpolation formula with remainder, the following is the successive differences of the n multiple integral from t0 to t of it, where 0≤m≤p−n.
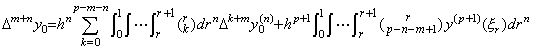 ____(4.67)
____(4.67)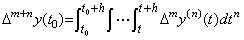
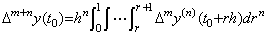 ________(4.68)
________(4.68)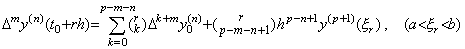
| [Q.E.D.] |
. . [Theorem 4.21]. .When the integers m and n satisfy 0≤m<n,
 _____(4.69)
_____(4.69)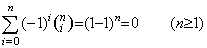
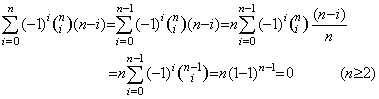
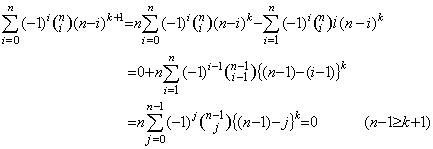
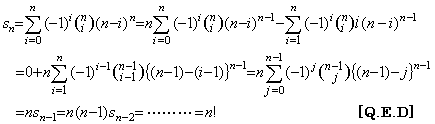
. . [Theorem 4.22]. .Denoting the coefficient of Δk+my0(n) of Eq.(4.67) by akn,
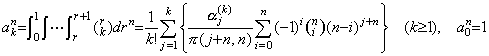 _____(4.70)
_____(4.70)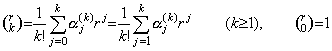 ______(4.71)
______(4.71)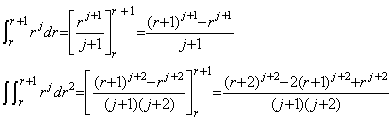
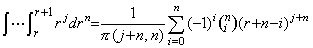 _____(4.72)
_____(4.72)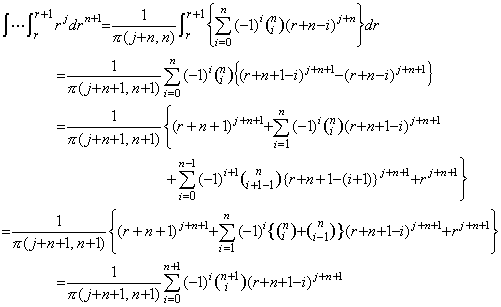
| [Q.E.D.] |
. .
By Theorem 4.20 and 4.22, it is able to express the relation between the vectors of y(n)(t) and Δny(t) in the following matrix equation, arranging the equations expressed in Eq.(4.67) with the m values such that 0≤m≤p−n.
 __(4.73)
__(4.73)where. .
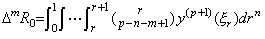
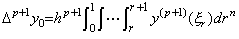 ______(4.74)
______(4.74)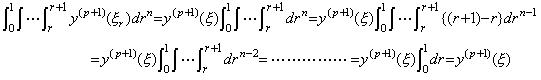
. .
[Theorem 4.23]. .If both y(t) and g(t) are continuous and g(t) does not change the sign in the interval between t0 and t, there exists a value ξ such that,
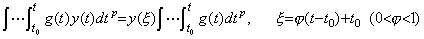 ____(4.75)
____(4.75)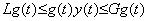
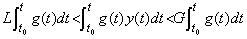
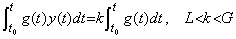
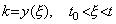
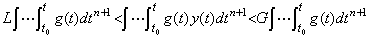
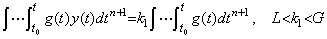
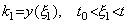
In case of g(t)<0, the proof is also shown in a similar way.______[Q.E.D.]
. . Denoting the innermost integral of the remainder ΔmR0 by f(r), by Theorem 4.17 there exists a value u such that,
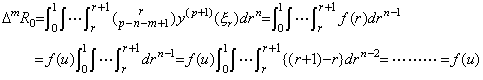
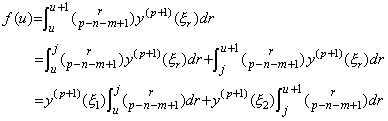
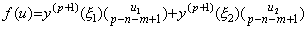
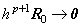
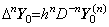 ______(4.76)
______(4.76)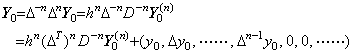 _____(4.77)
_____(4.77). . The transformation was the start how the author found this operational calculus. It is expressed in the matrix equation similar to this operational calculus but the matrix is not the operator of this operational calculus because the operand is the vector whose elements are not successive differences but successive derivatives at the initial point. It is the operator interfacing usual numerical calculus with this operational calculus. The details will be mentioned in Chapter 4.
. . The operator hnD−n of Eq.(4.76) obtains the n multiple integral from t0 to tp by use of the integrand from t0 to tp−n because the matrix D−n is of order p−n+1. Hence it is the predictor which predicts the n multiple integral from tp−n to tp. When the matrix D−n of Eq.(4.77) is of order p+1, premultiplying Eq.(4.77) by Δn,
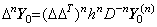 ________(4.78)
________(4.78). .
[Theorem 4.24]. .The following is always held independently on the remainder.
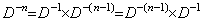 _______(4.79)
_______(4.79)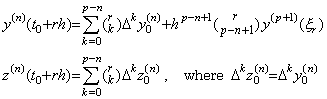
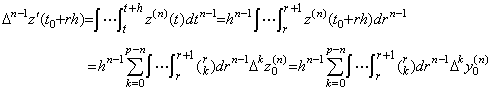
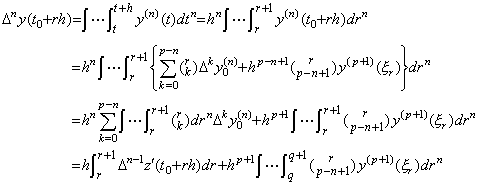
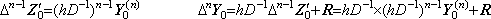
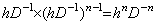
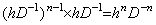 ________[Q.E.D.]
________[Q.E.D.]. . Accordingly, the n multiple integral may be carried out by n times use of the single integral program. In the case, there is no need to transform the initial values from y0' to y0(n−1) into the differences from Δy0 to Δn−1y0, because the successive integrals are,
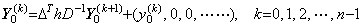 _____(4.80)
_____(4.80)