The differential operator (c) 1998 Akio Wakabayashi

3. Introducing the differential operator.
3.1 Summary explanation of the differential operator.
. . If the function y(t) is continuously differentiable, the vectors Y and Y' are obtained by the finite differences of the function and the first derivative. The relation of the vectors are expressed in the matrix equation Y' =AY. The matrix A is not the expansion of a vector because the differentiation is not a function. It is a quotient without vector form or an operator except quotient. Hence it is not able to calculate the matrix A by only the two vectors Y and Y' . It must be calculated by use of the vectors of all the continuous differentiable functions and the first derivatives.
. . If the function is constant, that is, y(t)=c₀, the derivative is y' (t)=0. Hence the matrix equation is 0=Ac₀1. It requires the first column of the matrix A to have the elements which are all zero. If the function is y(t)=c₀+c₁t, the derivative is y' (t)=c₁. Hence the matrix equation is c₁1=A(c₀, c₁h, 0, ……). It requires the second column to have the elements which are all zero except the first element is 1/h. If the function is y(t)=c₀+c₁t+c₂t², the derivative is y' (t)=c₁+2c₂t. Hence, Eq_a

___∴_

___∴_

If the function is y(t)=c₀+c₁t+c₂t²+c₃t³, the derivative is y' (t)=c₁+2c₂t+3c₃t². Hence,
Eq_d

___∴_

∴_

. . The more iterations give the differential operator which the author will denote as (1/h)ΔD, where the triangular matrix ΔD has the first row expressed below and the other rows whose elements are of the same as the upper row except those are shifted to the right by one cell.

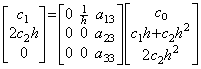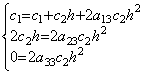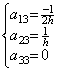
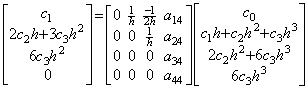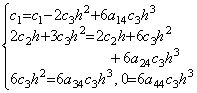
. . However, it is hard to make the proof that the matrix is held for all the continuous differentiable functions by this way. The proof is made by use of Newton's interpolation formula with remainder term and its derivative, if the functions are the continuous (p+1)th differentiable functions. Hence this operational calculus treats of differentiating such functions hereafter.

3.2 Newton's interpolation formula with remainder term.
. . It is usual for the remainder term of Newton's interpolation formula to be obtained by use of the term which has no meaning at the equidistant points by the reason that the denominator comes to zero. It causes trouble to the differentiation of the formula. Therefore the author obtains Newton's interpolation formula with remainder term by no use of the troubled term, supposing the range [a, b] has p+1 equidistant points with the interval h.

. . [Theorem 3.1]__When y(t)∈C^p+1[a, b], if t=t₀+qh∈[a, b] for any real number q,

_____(3.1) [Proof]__Supposing the remainder term at t=t₀+qh is,

_____(3.2) it satisfies the condition that the remainder must be zero at q=0, 1, 2, ……, p. Hence, Eq3_3

_____(3.3). . The denotation R is a function of q. Considering the approximated formula whose R is the constant R_q, where R_q denotes the R value for a noninteger value q, the function F(u) expressing the difference of y(t) and the approximated formula for t=t₀+uh is,
Eq3_4

_____(3.4). . The function F(u) comes to zero for the p+2 points of u=0, 1, 2, ……, p and q. Therefore, F^(p+1)(u)=0 is satisfied at a point between the minimum and the maximum of these u by Rolle's theorem. Denoting the point by ξ=t₀+uh,

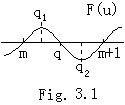_____(3.5) Fig3_1

. . It is shown as follows that Eq.(3.5) is also held for an integer q. Supposing m<q<m+1 for an integer m, the function F(u) is summarily figured in Fig. 3.1 around here. Because the function R is continuous by Eq.(3.3), there exist R→R_m and ξ→ξ_m for q→m and,

_____(3.6)
Therefore Eq.(3.5) is held at equidistant points m.__________[Q.E.D.]

__ [Theorem 3.2]____ _______(3.7)
[Proof]__Substituting q=p+1 to Eq.(3.1), there exists the value ξ_p+1 which satisfies Eq.(3.6), because it is able to carry out m=p and q→m+1 in Fig. 3.1, where the function F(u) does not intersect the abscissa at m+1. Hence,

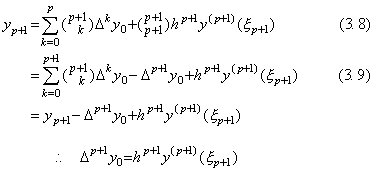[Q.E.D.]

. . When the range [a, b] has the p+1 intervals with the equidistance h, the function y(t) is expressed in Eq.(3.1) on the range [a, b−h] and the remainder terms are zero at y₀, y₁, ……, y_p. However, the value y_p+1 on the extension has the remainder term which is usually not zero as expressed in Eq.(3.8) and is given by Δ^p+1y₀. Therefore the value y_p+1 exists on the function of (p+1)th degree as expressed in Eq.(3.9). If y^(p+1)(t)≡0, the function y(t) is p-th degree. If there exists such a value M as |y^(p+1)(t)|≤M, it is satisfied that Δ^p+1y₀→0 for h→0 and the value y_p+1 exists on the function of p-th degree with the enough accurate approximation in case of small h. Accordingly, the function y(t) is able to be expressed in Eq.(3.1) without the remainder term and in the vector as follows in the range [a, b].

_____(3.10). . If it is not able to ignore Δ^p+1y₀ for y_p+1, the function must be approximated by the interpolation formula of higher than or equal to (p+1)th degree. However, if the function y^(p+1)(t) is not differentiable any more, we must divide the range [a, b] into smaller ranges and approximate the function y(t) by the interpolation formula of p-th degree.
. . It is generally hard to obtain the correct value of the remainder term of Eq.(3.1). Substituting Δ^p+1y₀ for h^p+1y^(p+1)(ξ) of the remainder term approximately by above property of Δ^p+1y₀, the result comes to the interpolation formula of (p+1)th degree without remainder term. Hence it is able to consider Δ^p+1y₀ as the approximate accuracy of the interpolation formula over the range [a, b], if it is not zero. Accordingly, it is able to use that for the purpose of determining whether the degree and interval is proper or not and whether the solution is converged or not in solving differential equations by the method with variable degree and interval.
. . If the function y^(p)(t) is not differentiable, the remainder term is not obtained. Even the case, substituting Δ^p+1y₀ for h^p+1y^(p+1)(ξ) of Eq.(3.9), the value y_p+1 is correctly expressed in the interpolation formula of (p+1)th degree without remainder term. Accordingly, it may be able to consider that the uppermost difference Δ^p+1y₀ gives the accuracy of approximation of the function by the interpolation formula of p-th degree over the range [a, b]. However, it is not certain whether Δ^p+1y₀→0 is certified or not, because the theorem 3.2 is not held in the case.
. . For example, Eq.(3.11) is one of the solutions of the differential equation y' = √y, y₀=0, which are mentioned in Chapter 1 Section 3.4.

_____(3.11) It is a function in C¹[0, 2] because the second derivative is not continuous at t=1. It comes to y"(t)=0 for t≤1 and y"(t)=1/2 for t>1. Dividing the range into two equidistant intervals with h=1, the function is expressed in Eq.(3.1) with p=1 in the range [0, 1], where the remainder term is zero. The value y₂ on the extension requires the value R of the remainder term to be Δ²y₀=1/4 and the function y(t) may be approximated in Eq.(3.12) over the range [0, 2]. The theorem 3.1 and 3.2 is not held in this case and the value R is equal to the average of the two values h²y"(t).

_____(3.12). . Dividing the range into three equidistant intervals with h=2/3, the function is expressed in Eq.(3.1) with p=2, y₀=Δy₀=0 and Δ²y₀=1/36 in the range [0, 4/3], where the remainder term is not zero whereas y⁽³⁾(t)≡0. The value y₃ on the extension requires the value R of the remainder term to be Δ³y₀=1/6. In the case, the function y(t) may be approximated by the interpolation formula of third degree as in Eq.(3.13) over the range [0, 2].

_____(3.13). . Dividing the range into four equidistant intervals with h=1/2, the function is expressed in Eq.(3.1) with p=3, y₀=Δy₀=Δ²y₀=0 and Δ³y₀=1/16 in the range [0, 3/2], where the remainder term is not zero whereas y⁽⁴⁾(t)≡0 and Δ⁴y₀=0. Substituting Δ⁴y₀=0 for R, the function y(t) is also approximated by the formula of third degree as in Eq.(3.14) over the range [0, 2]. However, it is not equal to both of Eq.(3.13) and Eq.(3.11).

_____(3.14). . In the interpolation formula of higher degree than the continuous differentiable order of a given function, the upper most difference does not give the correct estimation of accuracy of the formula as mentioned above. Accordingly, we must use the interpolation formula of lower degree by dividing the range into smaller ranges. In above example, we obtain the best result when the range is divided into [0, 1] and [1, 2]. Therefore the differential equation mentioned above must be solved for the case that the solution is always zero and for the case that the solution is not always zero as mentioned in Chapter 1 Section 3.4.

3.3 The difference of Newton's interpolation formula.
. . Expressing the subtraction of the function y(t)∈C^p+1[a, b] from the shifted function y(t+h) in Δy(t)=y(t+h)−y(t), the function Δy(t) is what gives the differences Δy₀, Δy₁, Δy₂, ……… for the values t₀, t₁, t₂, ……… with equidistant interval h and is expressed in the difference of vectors.

. . [Theorem 3.3]. .When y(t)∈C^p+1[a, b], for any real number r such that t=t₀+rh∈[a, b],

_____(3.15) [Proof]. .Because the function y(t+h) is what we obtain by shifting y(t) in parallel with the axis t by −h, it is expressed in following interpolation formula by shifting Eq.(3.3) and the remainder term comes to zero at the p+1 points of q=−1, 0, 1, 2, ………, p−1.
Eq3_16

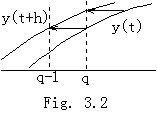_____(3.16) Fig3_2

. . Because the value y(t+h) for q−1 is equal to the value y(t) for q, the value R_h for q−1 is equal to the value R for q in Eq.(3.3). Accordingly, if the value of the function R_h is set to the constant R_q which was set in Eq.(3.4), the difference of the approximate formula from the function in Eq.(3.16) for t=t₀+uh is expressed in Eq.(3.17) and the function G(u) comes to zero at the p+2 points of u=−1, 0, 1, 2, ………, p−1 and q−1 because of G(u)=F(u+1).
Eq3_17

_____(3.17)
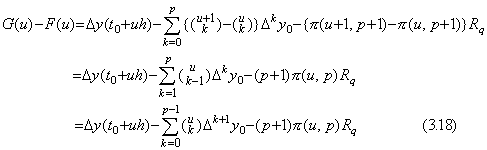
Eq3_18

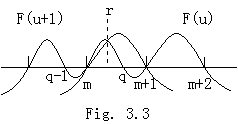
. . The function G(u)−F(u) comes to zero at the p+1 points of u=0, 1, 2, ………, p−1 and r such that q−1<r<q as in Fig. 3.3. Therefore the p-th derivative comes to zero at a value between the minimum and the maximum of these u values by Rolle's theorem. Supposing it is ξ=t₀+uh,

Because y^(p)(t) is differentiable once more, there exists a value ξ_r such that ξ<ξ_r<ξ+h and,

, where G(r)−F(r)=0 is satisfied in Eq.(3.18). Therefore Eq.(3.15) is satisfied for any noninteger r. It is also held for integer r, because we obtain r→m by carrying out q→m when m<r<q or q→m+1 when q−1<r<m as in Fig. 3.3.

______________________________________[Q.E.D.]

. . The remainder term of Eq.(3.15) is zero for the integer r such that r<p. In case of r=p, it is not always zero and Δy_p is expressed as follows. Therefore the (p+1)th difference is equal to the remainder term.
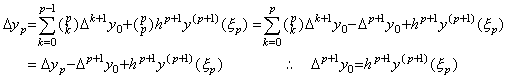
Eq3_18c

. . When the function y(t) is expressed in the vector Y₀, the (p+1)th difference comes to Δ^p+1y₀→0 because of h^p+1y^(p+1)(t)→0. Hence the function Δy(t) may be expressed in the formula of (p−1)th degree, which is equal to Eq.(3.15) without the remainder term in the range [a, b]. Accordingly, it may be expressed in following vector.

_____(3.19). . Supposing ΔY₀ is the product of a scalar Δ and the vector Y₀=(y₀, Δy₀, Δ²y₀, ……, Δ^py₀), the last element of the product is Δ^p+1y₀. It is equivalent to that of the difference ΔY₀=Y₁−Y₀. However, it may be omitted in the expression of the vector ΔY₀, because of Δ^p+1y₀→0. Accordingly, the last elements of the vector Y₁ and Y₀ are equivalent, that is, Δ^py₁=Δ^py₀. In practice, the denotation Δ of ΔY₀ is the operator expressed in matrix and above relations is expressed as follows.
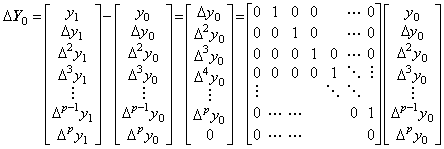Eq3_20

___(3.20)

3.4 Differentiation of Newton's interpolation formula.
. . Because of y' (t)∈C^p[a, b] when y(t)∈C^p+1[a, b], the derivative must be expressed in Newton's interpolation formula with remainder term by use of the differences up to Δ^p−1y₀' . Accordingly, the formula has less degree by one than the formula of y(t). In order to obtain the relation between y(t) and y' (t), the equidistant interval h must be of the same so the range [a, b] must be divided into p+1 equidistant intervals.

. . [Theorem 3.4]. .When y' (t)∈C^p[a, b], for any real q such that t=t₀+qh∈[a, b],

____(3.21) [Proof]. .Substituting y' (t) for y(t) and p−1 for p in the proof of Theorem 3.1, Eq.(3.3) and Eq.(3.4) come to following expressions.
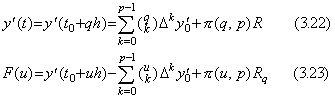
Eq3_22

. . If the value q is not integer, the function F(u) comes to zero at the p+1 points of u=0, 1, 2, ………, p−1 and q. Hence the p-th derivative comes to zero at a point between the maximum and minimum of these u values by Rolle's theorem. Supposing the value u is ξ' =t₀+uh,
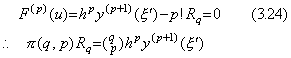
Eq3_24

. . If the value q is integer, the proof is completed by carrying out q→m for Eq.(3.24) as mentioned in the proof of Theorem 3.1. _____________________[Q.E.D.]

. . Substituting q=p for Eq.(3.21), Δ^py₀' comes to the remainder term by the method which is similar to the proof of Theorem 3.2 and it may be used in the remainder term of Eq.(3.21) instead of h^py^(p+1)(ξ' ) approximately.

_____(3.25). . When the vector Y₀ is defined by the members up to Δ^py₀, it is satisfied that h^py^(p+1)(t)→0 for h→0. Accordingly, the function y' (t) is approximated with enough accuracy in the range [a, b] by the formula of (p−1)th degree, that is, Eq.(3.21) without the remainder term. Therefore it is expressed in following vector.

_____(3.26)
. . The relation between Y₀' and Y₀ must be introduced by differentiating Newton's interpolation formula in Eq.(3.1). However, the differentiation must indirectly be carried out by use of the function F(u), because the derivative y^(p+1)(t) in the remainder term is not continuously differentiable as to t any more and the function ξ can not be expressed in q or t evidently.

. . [Theorem 3.5]. .When y(t)∈C^p+1[a, b], for any integer m such that t=t₀+mh∈[a, b],

_____(3.27) [Proof]. .When the formula Eq.(3.3) has the constant R_q which is the R value in the remainder term for any real number q such that m<q<m+1, the difference F(u) of the approximate formula from the function y(t) is expressed in Eq.(3.4). Differentiating it by u, the term with k=0 vanishes and it comes to,
Eq3_28

_____(3.28). . There exists a point q₁ such that F' (q₁)=0 for m<q₁<q as presented in Fig. 3.1 in the proof of Theorem 3.1. The point q₁ comes to q₁→m for q→m and there exists a value ξ_m such that ξ→ξ_m, because the derivative F' (u) is continuous as to the value u and the function R in the remainder term is continuous as to the value q. Hence,

_____[Q.E.D.]
. . It is evident from above proof that the derivative y' (t₀+rh) for noninteger r is expressed in as follows.
Eq3_29

___(3.29) Here, it is necessary to remember that the value ξ is not the value ξ_r which gives the remainder term of the value of the function y(t₀+rh) but the value ξ_q which gives the remainder term of the value of the function y(t₀+qh) for the value q such that m<r<q<m+1 and F' (r)=0.
. . The derivative dπ(u, p+1)/du is the sum of all the terms which are obtained by removing every one factor from π(u, p+1), so it does not come to zero even if the value u is integer less than p+1 because there exists always one of the terms. Accordingly, the remainder term of Eq.(3.27) does not come to zero at equidistant points if y^(p+1)(ξ_m) is not zero. The exponent of h is also less than that of the interpolation formula of y(t). Hence the numerical differentiation has less accuracy than the numerical approximation of function in general.

. . [Theorem 3.6]

______(3.30)
[Proof]. .1) If k=1, _____

2) If k=2, . .

3) If it is held for k=n, then for k=n+1,

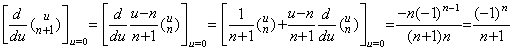[Q.E.D.]

. . By Theorem 3.5 and 3.6, the differential formula of Newton's interpolation formula with remainder term is expressed as follows at t=t₀.
Eq3_31

_____(3.31)

. . [Theorem 3.7]. .For integers m≥1 and k≥2,

, where for k=1,. .

____(3.32)
[Proof]. .It is held evidently for k=1 by the term 1 of the proof of Theorem 3.6.
Substituting u−1=v for k≥2,

_____[Q.E.D.]
. . In case of k≥2, the coefficient of the k-th term of y' _m is the sum of the coefficients of the (k−1)th and k-th terms of y' _m−1 by Theorem 3.7. Hence the differential formulas of Newton's interpolation formula with remainder term are obtained for t=t₀+mh in the order of increasing m from Eq.(3.31) as follows.
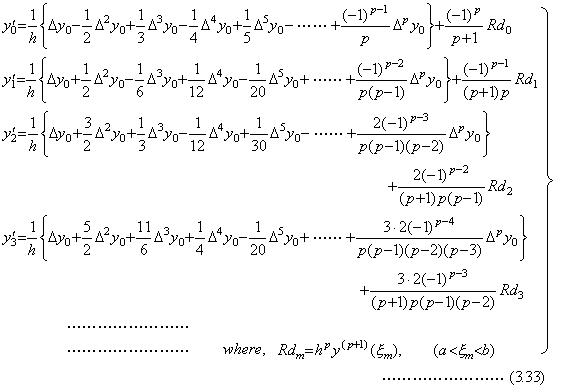
Eq3_33

. . The coefficients of above formulas are expressed in general form as mentioned in following two theorems.

. . [Theorem 3.8]. .For k≥m+1,

____(3.34) [Proof]. .When m=0, it is of the same as Theorem 3.6.
. . When m≥1, by Theorem 3.6 and 3.7,
1) When m=1, for k≥2,
Eq3_34a

2) If it is held for m=n and k≥n+1, in case of m=n+1 and k≥n+2,
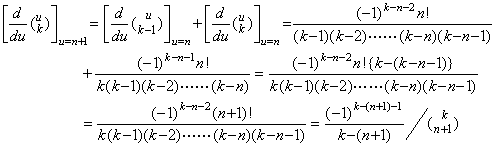Eq3_34b

[Q.E.D.]
. . When k≤m, the general form can not be expressed in the form of Theorem 3.8 because the denominator comes to zero. Hence it is expressed in the case for k−1<m of the series in Theorem 3.9.

. . [Theorem 3.9]

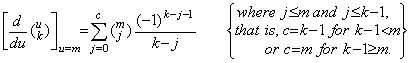_____(3.35) [Proof]

. .If m=0, the condition is c=0 for k≥1. Hence Eq.(3.35) comes to Theorem 3.6 because of j=0 and

. .If m=1, the condition is c=0 for k=1 or c=1 for k≥2. If k=1, the both sides of Eq.(3.35) come to the value 1.
If k=2,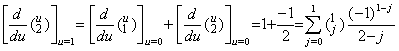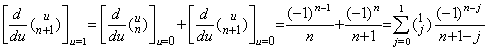
Eq3_35b

If Eq.(3.35) is held for k=n, it is also held for k=n+1 as follows.
Eq3_35c

Hence it is held for m=1.

. .If it is held for m=p, it is held for m=p+1 as follows.
If k=1, the both sides come to the value 1 because of c=0 for all m.
If k=2, the condition is c=k−1=1 because of m=p+1≥2. Hence,
Eq3_35d

If it is held for k=n, it is held for k=n+1 as follows. The condition as to the value c is determined as in Table 3.1 by the relation between the value n and p because it is equal to the less value of k−1 or m.

Table 3.1
	m=p and k=n	m=p and k=n+1	m=p+1 and k=n+1
n<p	k−1<m__∴ c=n−1	k−1<m__∴ c=n	k−1<m__∴ c=n
n=p	k−1<m__∴ c=n−1	k−1=m__∴ c=p=n	k−1<m__∴ c=n
n>p	k−1≥m__∴ c=p	k−1>m__∴ c=p	k−1≥m__∴ c=p+1

. . Hence it follows that there exist the two case of n≤p and n>p. If n≤p,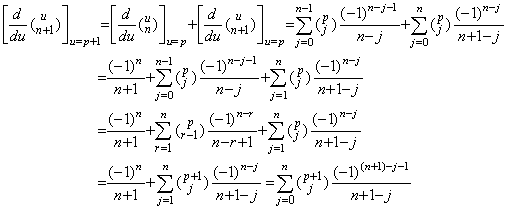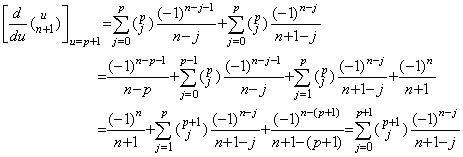
Eq3_35e

If n>p,

[Q.E.D.]

3.5 The differential operator.
. . Eq.(3.31) is the formula obtaining the value of derivative y₀' at t₀ from the values of function at all the equidistant points in the range [t₀, t_p]. The value of derivative y_m' at t_m may be obtained by the formula which uses the values of function at all the equidistant points in the range [t_m, t_m+p] and is expressed in Eq.(3.31) using the subscript m instead of the subscript 0. Accordingly,

where the remainder terms are expressed by use of Rd_m' for m≥1, because the values ξ in these remainder terms are different from those of Eqs.(3.33).
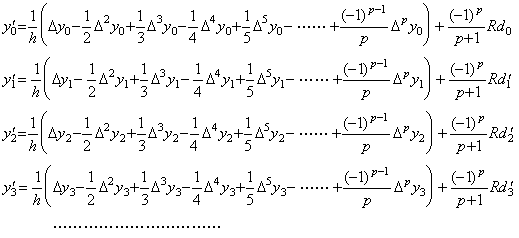
. . Calculating the difference of every order from above equations,
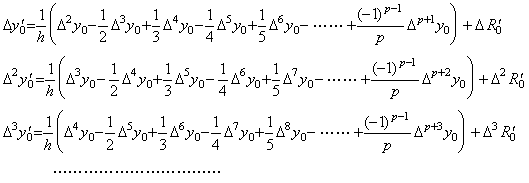
Eq3_5_b

. . However, if the difference Δ^my₀' needs to use the differences up to Δ^p+my₀ for m≥1, it means that it is not able to ignore the higher order differences so these should also be used in the expression of y₀' . Inversely speaking, the higher order differences than Δ^py₀ in the right sides of the equations Δ^my₀' should be included in the remainder terms, because the value y₀' may be expressed in the differences up to Δ^py₀. This is also evident from the definition of the vector Y₀, where the vector consists of the elements up to Δ^py₀ and the other higher order differences must be Δ^p+my₀→0 for m≥1. In accuracy, the proof is made by calculating the successive differences of the both sides of Eqs.(3.33) respectively. Hence it follows that the relation between Y₀ and Y₀' can be expressed in the relation over the same range [a, b].

. . [Theorem 3.10]. .Denoting the m-th difference of the remainder term of Eqs.(3.33) as Δ^mR₀,
if 0≤m≤p−1,

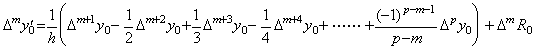
If m=p,______

(3.36)

[Proof]. .Expressing every equation of Eqs.(3.33) in general form,

where there exists the relation which are a_mk=a_m−1k−1+a_m−1k for m≥1 and k≥2 by Theorem 3.7 and a_m1=1 for m≥0 by Theorem 3.9. The m-th difference Δ^my₀' is obtained by calculating the m-th differences by respective terms in the right sides of the equations. It results to calculating the m-th differences of the coefficients of respective terms except the remainder term is denoted as Δ^mR₀.

1)	__If m=0, Eq.(3.36) is equivalent to the first equation of Eqs.(3.33).
2)	__If m=1, the first term with Δy₀ vanishes from the difference Δy₀' =y₁' −y₀' because the coefficient is Δa₀₁=a₁₁−a₀₁=1−1=0. The coefficient of every term with k≥2 comes to the coefficient of the term with k−1 in the case m=0, because it is Δa_0k=a_1k−a_0k=a_0k−1. Hence,
3)	__If m=2, the first term with Δy₀ vanishes from the second difference Δ²y₀' =y₂' −2y₁' +y₀' because the coefficient is Δ²a₀₁=a₂₁−2a₁₁+a₀₁=1−2+1=0. The second term with Δ²y₀ also vanishes because the coefficient is, . . The coefficient of every term with k≥3 comes to the coefficient of the term with k−1 in the case m=1, because of Hence,
4)	__Supposing Eqs.(3.36) is held for m=n, The coefficients are zero up to the term with Δⁿy₀. Hence,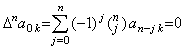 _for 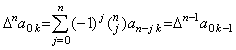k≤n, . ._for k>n and . . 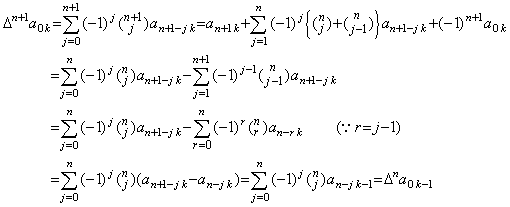Accordingly if m=n+1, where Δⁿ⁺¹a_0k=0 if k≤n+1 because Δⁿa_0k−1=0 for k−1≤n by the supposition. Therefore,
5)	__In above case, the integer k must be 1≤k≤p. Hence if n+1=p, the above equation comes to Δ^py₀' =Δ^pR₀ because all the terms with Δ^ky₀ has vanished by the reason that the suffix of the coefficient is p−n−1=0.______________________________________[Q.E.D.]

. . By Theorem 3.10, it is able to express the relation between the vectors of the function y and the derivative y' in the matrix equation Eq.(3.37). The p-th difference Δ^py₀' does not appear in the components of the vector Y₀' because it does not depend on the components of the vector ΔY₀. The last component Δ^pR₀ of the remainder vector is also omitted because it does not affect any component of the vector Y₀' except for Δ^py₀' .
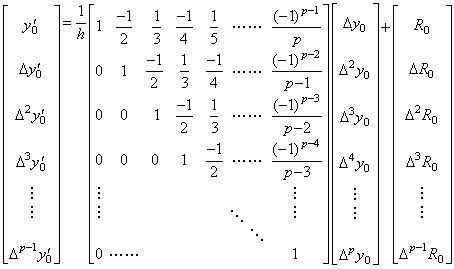Eq3_37

__(3.37). . The vector R₀, which denotes the remainder of Eq.(3.37), consists of the components which are the successive differences of the product of following two functions, because the remainders of Eqs.(3.33) have the coefficients for k=p+1 in respective case of m=0, 1, 2, ……, p−1, p in Theorem 3.8. Hence it can be expressed in the product of the vectors into which the respective functions are transformed.

______

_____(3.38). . The successive differences of the left function of m is equivalent to the coefficient of Δ^p+1y₀ if p+1 is substituted for p in Theorem 3.10, because Theorem 3.7 is held in the relation between the coefficients of Δ^py₀ and Rd_m in Eqs.(3.33). Hence the vector into which the left function is transformed is equivalent to the last column of the matrix of Eq.(3.37), if p+1 is substituted for p of the column. Accordingly, expanding the right vector of the product of two vectors into the matrix by the commutative law, the remainder vector comes to, Eq3_38b

where the last components of these vectors are omitted in Eq.(3.37).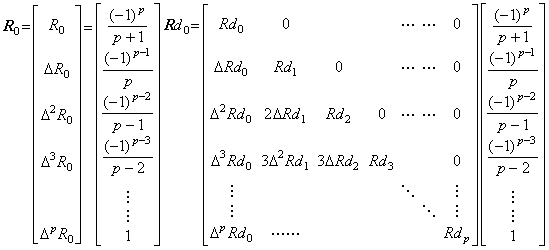
. . The magnitude of a vector is the maximum absolute value of the principal diagonal elements of the expanded matrix. Hence,

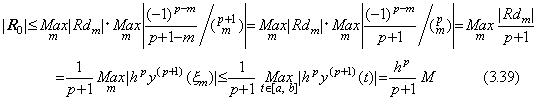
The condition R₀→0 is satisfied by y^(p+1)(t)≡0 or h→0 when it is able to express the function y(t) in the vector Y₀. Hence the p-th difference Δ^py₀' satisfies Δ^py₀' =Δ^pR₀→0 in Theorem 3.10.
. . The vector ΔY₀ is equivalent to the product of the operator Δ and the vector Y₀. The matrix of Eq.(3.37) is the upper triangular matrix whose rows have all the same elements, which are shifted to the right by one cell from the upper row. That is of the same property as the matrix A mentioned in Section 2.3 The difference operator. Accordingly, denoting the matrix of Eq.(3.37) as the symbol D, the product of the matrix D and the operator Δ is commutative, that is, DΔ=ΔD. Therefore Eq.(3.37) may be expressed in Eq.(3.40) symbolically.

______(3.40). . If the vector Y₀ is zero, the vector Y₀' comes to zero. However, even if the vector Y₀ is a constant vector and not zero, that is, Y₀=(y₀, 0, 0, ……), the vector Y₀' comes to zero. Accordingly, the matrix ΔD/h is not the quotient of the vector Y₀' and Y₀ but the operator. Therefore it is the differential operator. The matrix D is also the operator which is the quotient of the differential operator by the operator Δ/h.
. . When the associative law D(ΔY₀)=(DΔ)Y₀ is carried out in the mid side of Eq.(3.40), the vector Y₀ has the p+1 components of y₀ to Δ^py₀, whereas the difference vector ΔY₀ has the p components of Δy₀ to Δ^py₀. The right side of above equation is equivalent to the equation which has the product of zero and Δ^my₀ as the first term in the parentheses of Eq.(3.36). Hence the matrix DΔ has the (p+1)² elements and the first column and last row have all the elements of zero. This is the matrix ΔD mentioned in Section 3.1 Summary explanation of the differential operator.
. . Accordingly, the matrix D must have the (p+1)² elements which are the p² elements of the matrix in Eq.(3.37) and the elements of the column appended after the last column and of the row appended under the last row. The new last column has the elements expressed in Eq.(3.41) and the new last row has the elements of zero except the last element is one.

______(3.41) Hence the vector ΔY₀ must also have the p+1 components, where the last component is Δ^p+1y₀=0. Accordingly, the left side of the associative law is equivalent to the equation appended the product of Eq.(3.41) and zero after the last term in the parentheses of Eq.(3.36).
. . The matrix ΔD is the product of the matrix Δ and D. Hence the rightest side of Eq.(3.40) corresponds to the expression in Eq.(3.42), where it has the product of Eq.(3.41) and Δ^p+1y₀ as the last term in the parentheses of Eq.(3.36) and takes the symbol Δ outside the parentheses. The last term comes to zero if the symbol Δ is distributed into the parentheses because of Δ^p+1y₀=0. Although the operator Δ is different from the symbol Δ which denotes the numerical difference, it is able to suppose the multiplication of the operator Δ to a vector as the usual product of a scalar and a vector when the components of the vector are expressed in symbolical form as Δ^ky₀.
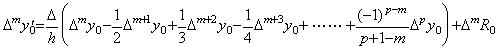Eq3_42

____(3.42) These relations should be explained in rigorous speaking in case of using the difference operator. However these may be omitted in usual case because there exists no confusion in result. Accordingly, these relations are being expressed in Eq.(3.40) implicitly.

Return to CONTENTS

3.6. .The second differential operator