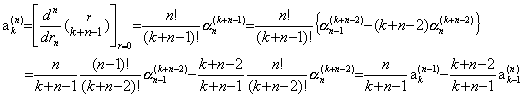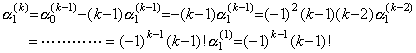3.6 The second differential operator.
. .
When there is a function y(t) such that y(t)∈Cp+1[a, b], the derivative is y' (t)∈Cp[a, b] and must be expressed in Newton's interpolation formula Eq.(3.21), because the equidistant points at which the remainder comes to zero are decreased to the p points of t0 to tp−1, where the formula of y(t) has p+1 points. In a similar way, the second derivative is y"(t)∈Cp−1[a, b] and the equidistant points at which the remainder comes to zero are decreased to the p−1 points of t0 to tp−2. Accordingly, it is expressed in Newton's interpolation formula as follows.. .
[Theorem 3.11]. .When y"(t)∈Cp−1[a, b], for any real q such that t=t0+qh∈[a, b],
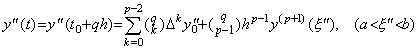 ____(3.43)
[Proof]. .Substituting y"(t) and p−2 for y(t) and p respectively at the proof of Theorem 3.1, Eq.(3.3) and the residual F(u) in Eq.(3.4) come to, ____(3.43)
[Proof]. .Substituting y"(t) and p−2 for y(t) and p respectively at the proof of Theorem 3.1, Eq.(3.3) and the residual F(u) in Eq.(3.4) come to,
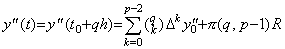 ________(3.44) ________(3.44)
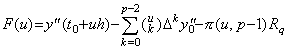 ________(3.45)
The residual F(u) comes to zero at the p points of u=0, 1, 2, ……, p−2 and q. Hence the (p−1)th derivative comes to zero at a point between the maximum and minimum of these points by Rolle's theorem. Supposing the point is ξ"=t0+uh, ________(3.45)
The residual F(u) comes to zero at the p points of u=0, 1, 2, ……, p−2 and q. Hence the (p−1)th derivative comes to zero at a point between the maximum and minimum of these points by Rolle's theorem. Supposing the point is ξ"=t0+uh,
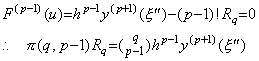 The remainder is also held in the case when the value q is integer. The proof is made in the similar way mentioned in Eq.(3.6).___________________[Q.E.D.]
The remainder is also held in the case when the value q is integer. The proof is made in the similar way mentioned in Eq.(3.6).___________________[Q.E.D.]. .
In the similar way with the proof of Theorem 3.2, it is able to show that the (p−1)th difference Δp−1y0" is expressed in the formula with only the remainder term as follows.
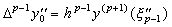 ________(3.46)
When |y(p+1)(t)|≤M is satisfied, the (p−1)th difference satisfies Δp−1y0"→0 for h→0 and the second derivative y"(t) can be approximated by the function of (p−2)th order with sufficient accuracy. Hence it is expressed in the vector as follows. ________(3.46)
When |y(p+1)(t)|≤M is satisfied, the (p−1)th difference satisfies Δp−1y0"→0 for h→0 and the second derivative y"(t) can be approximated by the function of (p−2)th order with sufficient accuracy. Hence it is expressed in the vector as follows.
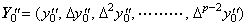 ________(3.47)
The relation between the vector Y0" and Y0' must be obtained by differentiating Newton's interpolation formula of y' (t) in Eq.(3.21). The differentiation must be carried out indirectly by use of the residual F(u) in Eq.(3.23). ________(3.47)
The relation between the vector Y0" and Y0' must be obtained by differentiating Newton's interpolation formula of y' (t) in Eq.(3.21). The differentiation must be carried out indirectly by use of the residual F(u) in Eq.(3.23).. .
[Theorem 3.12]. .When y' (t)∈Cp[a, b], for any integer m such that t=t0+mh∈[a, b],
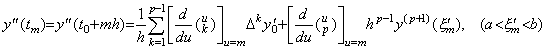 _____(3.48)
[Proof]. .There exists the residual F(u) expressed in Eq.(3.23) between the derivative y' (t) and the interpolation formula with the approximate remainder except at a real q such that m<q<m+1. Differentiating it by the variable u, the derivative is expressed in Eq.(3.49) because the term with k=0 vanishes and the value Rq is constant as to the variable u. _____(3.48)
[Proof]. .There exists the residual F(u) expressed in Eq.(3.23) between the derivative y' (t) and the interpolation formula with the approximate remainder except at a real q such that m<q<m+1. Differentiating it by the variable u, the derivative is expressed in Eq.(3.49) because the term with k=0 vanishes and the value Rq is constant as to the variable u.
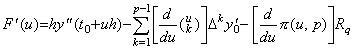 ______(3.49)
The residual F(u) is expressed in the graph which is similar to Fig. 3.1 around the point q. Hence the derivative F' (u) comes to zero for a value q1 such that m<q1<q. The point q1 comes to q1→m for q→m and there exists a value ξm' such that ξ' →ξm' and F' (m)=0, because the sequence of F(u) as to q is continuous. Here the value Rq is given by Eq.(3.24) as follows. ______(3.49)
The residual F(u) is expressed in the graph which is similar to Fig. 3.1 around the point q. Hence the derivative F' (u) comes to zero for a value q1 such that m<q1<q. The point q1 comes to q1→m for q→m and there exists a value ξm' such that ξ' →ξm' and F' (m)=0, because the sequence of F(u) as to q is continuous. Here the value Rq is given by Eq.(3.24) as follows.
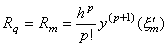 _______________[Q.E.D.] _______________[Q.E.D.]
. .
Theorem 3.10 is also held when y0", y0' and p−1 are substituted for y0' , y0 and p respectively, because the coefficients of Eq.(3.48) hold Theorem 3.6, 3.7, 3.8 and 3.9. Hence the successive differences of Eq.(3.48) are expressed as follows.
If 0≤m≤p−2,
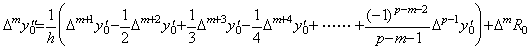
and if m=p−1, ____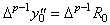 __________(3.50). .
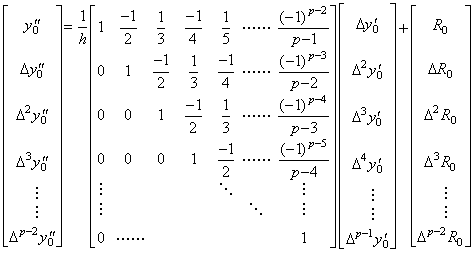
Expressing the successive differences in matrix equation, __________(3.50). .
Expressing the successive differences in matrix equation,
 ___(3.51). .
Eq.(3.38) and (3.39) are also held when y0", y0' and p−1 are substituted for y0' , y0 and p respectively, where the value ξm is different. Accordingly, ___(3.51). .
Eq.(3.38) and (3.39) are also held when y0", y0' and p−1 are substituted for y0' , y0 and p respectively, where the value ξm is different. Accordingly,
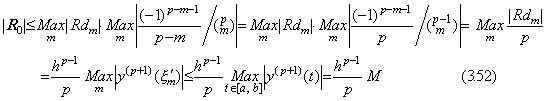 . .
The condition R0→0 is satisfied by y(p+1)(t)≡0 or h→0 when it is able to express the function y' (t) in the vector Y0' . Hence the (p−1)th difference satisfies Δp−1y0"=Δp−1R0→0 in Eq.(3.50). . .
The condition R0→0 is satisfied by y(p+1)(t)≡0 or h→0 when it is able to express the function y' (t) in the vector Y0' . Hence the (p−1)th difference satisfies Δp−1y0"=Δp−1R0→0 in Eq.(3.50).
. .
The matrix in Eq.(3.51) consists of the elements except of the last column and row of the matrix D in Eq.(3.37). However, the matrix is of the same as the matrix D and the last column and row are only being omitted by the reason that the components of Δpy0' and the differences of higher order come to all zero in the vector ΔY0' for h→0. Accordingly, substituting the rightest side of Eq.(3.40) for the vector Y0' , Eq.(3.51) comes to,
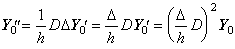 ______(3.53)
Therefore the author names (ΔD/h)2 as the second differential operator. ______(3.53)
Therefore the author names (ΔD/h)2 as the second differential operator.
. .
The second differential operator was obtained by the two steps of differentiating Newton's interpolation formula of y(t) and y' (t). It must be equivalent to the second differentiation of Newton's interpolation formula of y(t) by one step. The operator is expressed in Δ2D2/h2 and the matrix denoted as D2 is equal to the product D×D. These are shown by following theorems.. .
[Theorem 3.13]. .When y(t)∈Cp+1[a, b], for any real number r such that t=t0+rh∈[a, b],
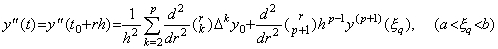 ___(3.54)
where ξq is the value which gives the remainder of Newton's interpolation formula of y(t) for some point t=t0+qh∈[a, b]. ___(3.54)
where ξq is the value which gives the remainder of Newton's interpolation formula of y(t) for some point t=t0+qh∈[a, b].
[Proof]. .When the constant Rq was substituted for the function R in the remainder of Eq.(3.3), the residual F(u) between the function y(t) and the approximate formula was expressed in Eq.(3.4) and expressed in Fig. 3.1 around u=q. The derivative F' (u) comes to zero at the points q1, q2 such that m<q1<q<q2<m+1. Hence the second derivative F"(u) expressed in Eq.(3.55) comes to zero for a point r such that q1<r<q2.
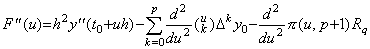 ____(3.55)
Hence at the point r, ____(3.55)
Hence at the point r,
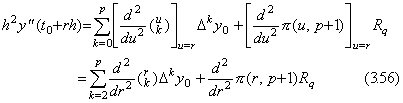 where the constant Rq is given by Eq.(3.5) as follows, denoting ξ by ξq.
where the constant Rq is given by Eq.(3.5) as follows, denoting ξ by ξq.
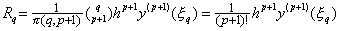 ________[Q.E.D] ________[Q.E.D]
. .
The point r where the second derivative is F"(r)=0 does not come to the equidistant point m for q→m, because the point q2 only approaches about the midpoint of the interval [m, m+1], though the point q1 approaches to the point m. When the point q has come to the left of the point m, the relation of these points comes to m−1<q<q1<m<q2<m+1 and the point r approaches about the point m but it is not certain that it comes to the point m. If the point q approaches to the point m+1 or m+2, the point r approaches about the point m+1 but it is not certain that it comes to the point m+1. However, there exists enough small value M which satisfies following condition by Eq. (3.55), because F"(u) is the second derivative of the residual between y(t) and its approximated formula.
|F"(u)|≤Mh2≤h2|y"(t0+uh)|max________∴. .|F"(u)|→0 for h→0
Accordingly, the values of the second derivatives at equidistant point m are expressed in following equation by denoting the remainder as Rm. The remainder approaches to zero for h→0.
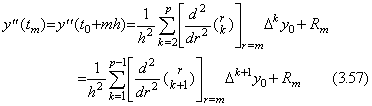
. .
[Theorem 3.14]. .For k≥1,
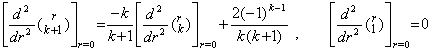 ____(3.58)
[Proof]. .Twice differentiating the product of a function f(r) and a linear equation g(r), by g"(r)≡0, ____(3.58)
[Proof]. .Twice differentiating the product of a function f(r) and a linear equation g(r), by g"(r)≡0,
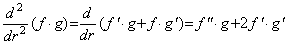 _____(3.59)
Therefore, _____(3.59)
Therefore,
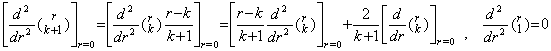 By Theorem 3.6,
By Theorem 3.6,
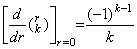 | [Q.E.D.] |
. .
Accordingly, the coefficients of the rightest side of Eq.(3.57) are obtained successively for m=0 and k≥1 as follows. They are one for k=1, (−2/3)+(2/3)(−1/2)=−1 for k=2, (−3/4)(−1)+(2/4)(1/3)=11/12 for k=3, (−4/5)(11/12)+(2/5)(−1/4)=−5/6 for k=4 and so on. . .
[Theorem 3.15]
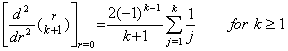 ______(3.60)
[Proof]. .If the linear equation is g(r)=r in Eq.(3.59), ______(3.60)
[Proof]. .If the linear equation is g(r)=r in Eq.(3.59),
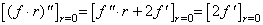 Therefore,
Therefore,
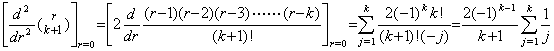
. .
[Theorem 3.16]. .For m≥1 and k≥2,
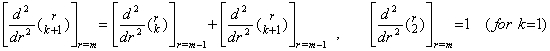 ____(3.61)
[Proof] ____(3.61)
[Proof]
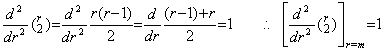 When k≥2, by the substitution r−1=u,
When k≥2, by the substitution r−1=u,
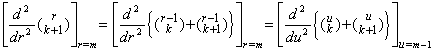
. .
[Theorem 3.17]. .For m≥1 and k≥m+1,
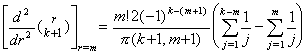 _____(3.62)
[Proof]. .1) If m=1, it is held for k≥2 by Theorem 3.15 as follows. _____(3.62)
[Proof]. .1) If m=1, it is held for k≥2 by Theorem 3.15 as follows.
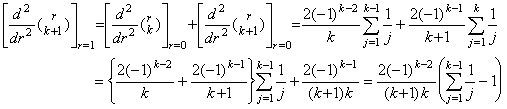 2) Supposing it is held for m=n and k≥n+1,
2) Supposing it is held for m=n and k≥n+1,
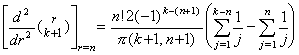 . .It is also held for m=n+1 and k≥n+2 as follows.
. .It is also held for m=n+1 and k≥n+2 as follows.
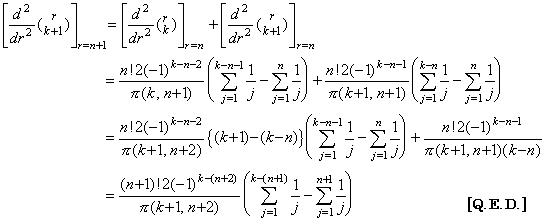
. .Accordingly, the value of the second derivative of Newton's interpolation formula is expressed in the following first formula at t=t0 by Eq.(3.57). The formulas at the other equidistant points are successively obtained as follows by above Theorems, where the coefficients of the last terms in the braces are the values of Eq.(3.62) for k+1=p.
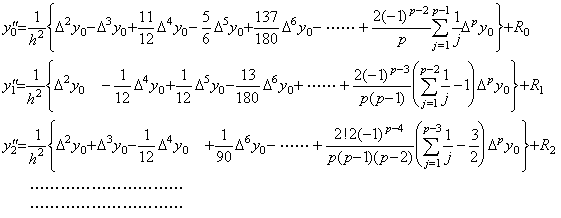 . .The successive differences of y"(tm) are obtained by those of the right sides of above equations. It results in obtaining the successive differences of the coefficients of Δk+1y0 with the same k value and results in Eq.(3.63) by use of the coefficients of above first equation, where the value m is less than or equal to p−2 and Δp−1y0"=Δp−1R0 is satisfied. The proof is easily shown by the proof of Theorem 3.10, because it only depends on the relation of the coefficients mentioned in Theorem 3.7 and Theorem 3.16 is of the same relation as it.
. .The successive differences of y"(tm) are obtained by those of the right sides of above equations. It results in obtaining the successive differences of the coefficients of Δk+1y0 with the same k value and results in Eq.(3.63) by use of the coefficients of above first equation, where the value m is less than or equal to p−2 and Δp−1y0"=Δp−1R0 is satisfied. The proof is easily shown by the proof of Theorem 3.10, because it only depends on the relation of the coefficients mentioned in Theorem 3.7 and Theorem 3.16 is of the same relation as it.
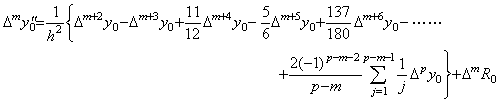 ___(3.63). .
Eq.(3.63) is able to be expressed in following matrix equation. ___(3.63). .
Eq.(3.63) is able to be expressed in following matrix equation.
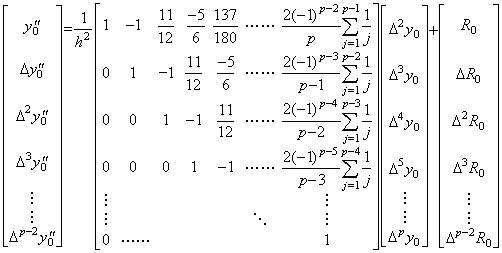 __(3.64). .
The remainder vector R0 is the product of following two functions of m for 0≤m≤p−1 because of k=p≥m+1, where it is supposed that the sum from j=1 to j=0 denotes zero. __(3.64). .
The remainder vector R0 is the product of following two functions of m for 0≤m≤p−1 because of k=p≥m+1, where it is supposed that the sum from j=1 to j=0 denotes zero.
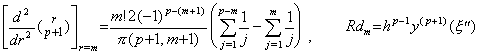 Hence,
Hence,
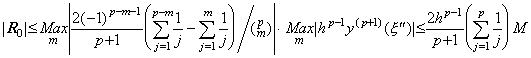 . .
The condition R0→0 is satisfied by y(p+1)(t)≡0 or h→0 when it is able to express the function y(t) in the vector Y0. Hence the (p−1)th difference satisfies Δp−1y0"=Δp−1R0→0. . .
The condition R0→0 is satisfied by y(p+1)(t)≡0 or h→0 when it is able to express the function y(t) in the vector Y0. Hence the (p−1)th difference satisfies Δp−1y0"=Δp−1R0→0.
. .
The vector Δ2Y0 is equivalent to the product of the operator Δ2 and the vector Y0. The matrix of Eq.(3.64) is the upper triangular matrix whose rows have all the same elements, which are shifted to the right by one cell from the upper row. Accordingly, denoting the matrix as the symbol D2, the product of the matrix D2 and the operator Δ2 is commutative and,
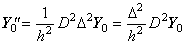 _______(3.65) _______(3.65). .
[Theorem 3.18]_____D2=D×D
[Proof]. .Denoting the k-th element in the first row of the operator D as dk, the k-th column of the operator D comes to the vertical vector expressed in,
(dk, dk−1, dk−2, ………, d2, d1, 0, 0, ………)
Hence the k-th element in the first row of the product D×D comes to,
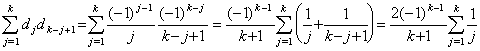 ____(3.66)
This is equal to the k-th element in the first row of the matrix denoted as D2 by Theorem 3.15. ____(3.66)
This is equal to the k-th element in the first row of the matrix denoted as D2 by Theorem 3.15.
. .
Denoting the k-th element in the j-th row of the operator D as djk, it is zero for k<j and dk−j+1 for k≥j. Hence the k-th element in the j-th row of the product D×D is zero in case of k<j, because of djm=0 for m<j and dmk=0 for m≥j. In case of k≥j, it comes to,
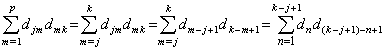 This is the (k−j+1)th element in the first row by Eq.(3.66). Therefore the j-th row of the product D×D is of the same as the first row except it is shifted to the right by j−1 cells and the product D×D is equal to the matrix D2.
This is the (k−j+1)th element in the first row by Eq.(3.66). Therefore the j-th row of the product D×D is of the same as the first row except it is shifted to the right by j−1 cells and the product D×D is equal to the matrix D2.
. .
The product D×D is the square matrix of order p, because the operator D is the square matrix of order p. On the other hand, the matrix denoted D2 is the square matrix of order p−1 as expressed in Eq.(3.64). However, the p-th column and row are only omitted from expression by the reason that Δp+1y0→0 is satisfied and Δp−1y0"→0 depends only on the remainder.
3.7 The differential operator of higher order.
. .
When there is a function y(t) such that y(t)∈Cp+1[a, b], the n-th derivative is y(n)(t)∈Cp−n+1[a, b]. Accordingly, when it is expressed in Newton's interpolation formula, the equidistant points at which the remainder comes to zero are decreased to the p−n+1 points of t0 to tp−n. . .
[Theorem 3.19]. .When y(n)(t)∈Cp−n+1[a, b], for any real q such that t=t0+qh∈[a, b],
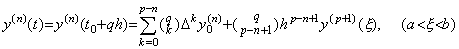 ___(3.67)
[Proof]. .The interpolation formula of y(n)(t) and the residual F(u) with the constant Rq, which is the R value for q, are expressed in, ___(3.67)
[Proof]. .The interpolation formula of y(n)(t) and the residual F(u) with the constant Rq, which is the R value for q, are expressed in,
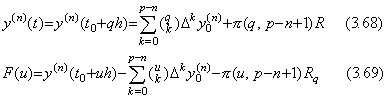 . .The residual F(u) comes to zero at the p−n+2 points of u=0, 1, 2, ……, p−n and q. Hence the (p−n+1)th derivative comes to zero at a point between the maximum and minimum of these points by Rolle's theorem. Supposing the point is ξ=t0+uh,
. .The residual F(u) comes to zero at the p−n+2 points of u=0, 1, 2, ……, p−n and q. Hence the (p−n+1)th derivative comes to zero at a point between the maximum and minimum of these points by Rolle's theorem. Supposing the point is ξ=t0+uh,
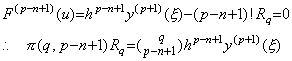 The remainder is also held in the case when the value q is integer. The proof is made in the similar way mentioned in Eq.(3.6)._________________________________[Q.E.D.]
The remainder is also held in the case when the value q is integer. The proof is made in the similar way mentioned in Eq.(3.6)._________________________________[Q.E.D.]. .
In the similar way with the proof of Theorem 3.2, it is able to show that the (p−n+1)th difference is expressed in the formula with only the remainder term as follows.
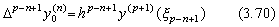 . .When |y(p+1)(t)|≤M is satisfied, the (p−n+1)th difference satisfies Δp−n+1y0(n)→0 for h→0 and the n-th derivative y(n)(t) can be approximated by the function of (p−n)th order with sufficient accuracy. Hence it is expressed in the vector as follows.
. .When |y(p+1)(t)|≤M is satisfied, the (p−n+1)th difference satisfies Δp−n+1y0(n)→0 for h→0 and the n-th derivative y(n)(t) can be approximated by the function of (p−n)th order with sufficient accuracy. Hence it is expressed in the vector as follows.
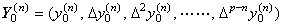 _____(3.71). .
The (n−1)th derivative y(n−1)(t) is expressed in Newton's interpolation formula by substituting n−1 for n of Eq.(3.67) as follows. _____(3.71). .
The (n−1)th derivative y(n−1)(t) is expressed in Newton's interpolation formula by substituting n−1 for n of Eq.(3.67) as follows.
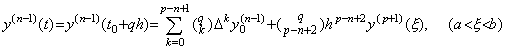 ___(3.72)
Hence it is expressed in the vector as follows. ___(3.72)
Hence it is expressed in the vector as follows.
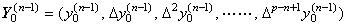 _____(3.73). .
Differentiating y(n−1)(t), the values y(n)(tm) at equidistant points are expressed in the successive differences of y(n−1)(tm) as follows by the similar proof as Theorem 3.12. _____(3.73). .
Differentiating y(n−1)(t), the values y(n)(tm) at equidistant points are expressed in the successive differences of y(n−1)(tm) as follows by the similar proof as Theorem 3.12.
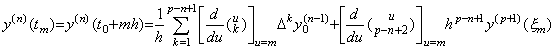
(a<ξm<b) | _____(3.74) |
. .
The successive differences of the both sides of above equations are expressed in Eq.(3.75) for 0≤m≤p−n and in Δp−n+1y0(n)=Δp−n+1R0 for m=p−n+1, where ΔmR0 denotes the successive differences of the remainder of Eq.(3.74), denoting them by Rm. This is evident by Theorem 3.6, 3.7, 3.8, 3.9 and 3.10.
 _____(3.75). .
Expressing the successive differences in matrix equation, _____(3.75). .
Expressing the successive differences in matrix equation,
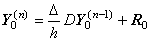 _____(3.76) _____(3.76)
. .
[Theorem 3.20]. .The n-th differential operator is,
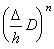 ________(3.77)
[Proof]. .It is already shown that it is held for n=1 and n=2. Supposing it is held for the (n−1)th differential operator, by Eq.(3.76), ________(3.77)
[Proof]. .It is already shown that it is held for n=1 and n=2. Supposing it is held for the (n−1)th differential operator, by Eq.(3.76),
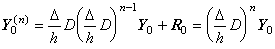 _____(3.78)
because substituting Rdm for hp−n+1y(p+1)(ξm), by Theorem 3.8, _____(3.78)
because substituting Rdm for hp−n+1y(p+1)(ξm), by Theorem 3.8,
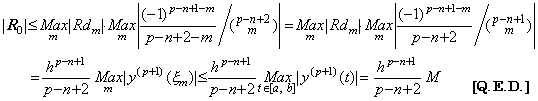
. .The n-th differential operator in Eq. (3.77) is obtained by differentiating Newton's interpolation formula of y(n−1)(t). It must be shown that it is equivalent to the operator obtained by n-th differentiating Newton's interpolation formula of y(t).
. .
[Theorem 3.21]. .When y(t)∈Cp+1[a, b] and 1≤n≤p, for any real number r such that t=t0+rh∈[a, b],
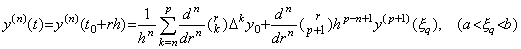 ___(3.79)
where ξq is the value which gives the remainder of Newton's interpolation formula of y(t) for some point t=t0+qh∈[a, b]. ___(3.79)
where ξq is the value which gives the remainder of Newton's interpolation formula of y(t) for some point t=t0+qh∈[a, b].
[Proof]. .It is already shown that it is held for n=1 and n=2. Let us suppose it is held for the (n−1)th derivative y(n−1)(t).
. .
The (n−1)th derivative of the residual F(u) expressed in Eq.(3.4) is expressed in Eq.(3.80) and it comes to zero at p−(n−1)+2 points because the residual comes to zero at p+2 points. Denoting these points by uk(k=1, 2, ……, p−n+3), the derivative of F(n−1)(u) comes to zero at a point between uk and uk+1. Denoting the point by r, the value of the derivative at r is obtained by Eq.(3.81).
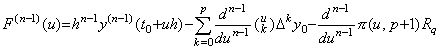 ____(3.80) ____(3.80)
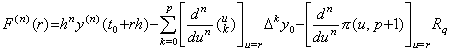 ____(3.81)
The constant Rq is given by Eq.(3.5) as follows. ____(3.81)
The constant Rq is given by Eq.(3.5) as follows.
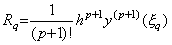
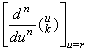 is equivalent to
is equivalent to
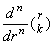 and it is zero for k<n.
and it is zero for k<n.
. .
The derivative F(n)(r) does not come to zero at points except for above p-n+2 points. However, there exists enough small value M which satisfies following condition by Eq. (3.81), because F(n)(r) is the n-th derivative of the residual between y(t) and its approximated formula. Therefore Eq.(3.79) is held for any r.
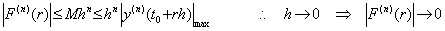 ____[Q.E.D.] ____[Q.E.D.]
. .
Accordingly, the values of the n-th derivatives at equidistant points are expressed in following equation, denoting the remainder by Rm.
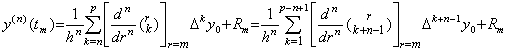 ___(3.82) ___(3.82)
. .
[Theorem 3.22]. .The n-th derivative of the product of a function f(r) and a linear equation g(r) is,
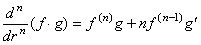 ______(3.83)
[Proof]. .It is evidently held for n=1 and for n=2 by the proof of Theorem 3.14. ______(3.83)
[Proof]. .It is evidently held for n=1 and for n=2 by the proof of Theorem 3.14.
Supposing it is held for n=k, by g"(r)≡0,
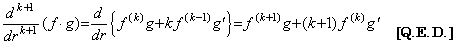
. .
[Theorem 3.23]. .Denoting the k-th coefficient of Eq.(3.82) with m=0 by ak(n),
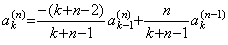 for k≥1 and n≥2, where a0(n)=0.____(3.84)
[Proof]. .In case of k≥1 and n≥2, by Eq.(3.83),
for k≥1 and n≥2, where a0(n)=0.____(3.84)
[Proof]. .In case of k≥1 and n≥2, by Eq.(3.83),
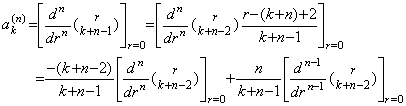 The n-th derivative of
The n-th derivative of
 is identical with zero because the function is of the (n−1)th order. Hence,
is identical with zero because the function is of the (n−1)th order. Hence,
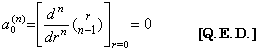
. .
These coefficients are expressed in Table 3.2 for p=10.
Table 3.2___The k-th coefficient of Eq.(3.82) for p=10 and m=0.
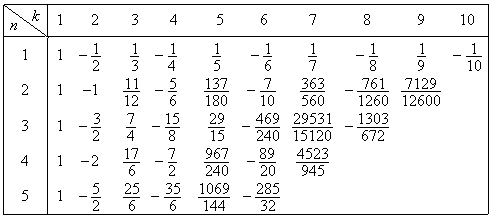
. .
[Theorem 3.24]. .Denoting the k-th coefficient of Eq.(3.82) by amk, it is expressed in Table 3.2 for m=0 and any n. For m≥1 and k≥2,
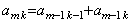 , where am1=1 for any m.____(3.85)
[Proof]. .It was shown by Theorem 3.7 and 3.16 for n=1 and n=2. Supposing it is held for the (n−1)th derivative, by Eq.(3.83), , where am1=1 for any m.____(3.85)
[Proof]. .It was shown by Theorem 3.7 and 3.16 for n=1 and n=2. Supposing it is held for the (n−1)th derivative, by Eq.(3.83),
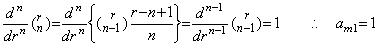 Substituting u for r−1 in case of k≥2,
Substituting u for r−1 in case of k≥2,

. .
[Theorem 3.25]. .Denoting the m-th difference of the remainder term of Eq.(3.82) as ΔmR0,
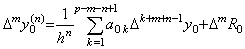 . .for 0≤m≤p−n,. . . .for 0≤m≤p−n,. .
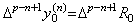 ____(3.86)
[Proof]. .Expressing Eq.(3.82) in the coefficients amk, ____(3.86)
[Proof]. .Expressing Eq.(3.82) in the coefficients amk,
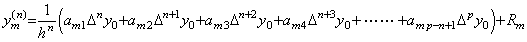 The m-th difference Δmy0(n) is obtained by calculating the m-th differences of the coefficients by respective terms in the right side. It results in Eq.(3.86). By Theorem 3.24, the Proof is of the same as Theorem 3.10 except there are ym(n) in the left side and Δny0 in the first term of the right side.
The m-th difference Δmy0(n) is obtained by calculating the m-th differences of the coefficients by respective terms in the right side. It results in Eq.(3.86). By Theorem 3.24, the Proof is of the same as Theorem 3.10 except there are ym(n) in the left side and Δny0 in the first term of the right side.
. .
Hence it is able to express Eq.(3.86) in the matrix equation,
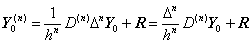 ______(3.87)
The matrix denoted by D(n) consists of the first row whose k-th element is a0 k and the p−n rows whose m-th row has a0 k−m as the k-th element, where a0 k−m denotes zero for k≤m. ______(3.87)
The matrix denoted by D(n) consists of the first row whose k-th element is a0 k and the p−n rows whose m-th row has a0 k−m as the k-th element, where a0 k−m denotes zero for k≤m.
. .
The remainder comes to R→0 for h→0, because the coefficient am p−n+2 in the remainder term of Eq.(3.82) is,
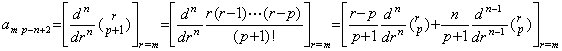 and there exists a value βn such that,
and there exists a value βn such that,
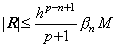 , _____where |y(p+1)(t)|≤M , _____where |y(p+1)(t)|≤M
. .
[Theorem 3.26]. .The matrix denoted by D(n) is the product of the n operators denoted by D, that is,
D(n)=D×D×………×D.
[Proof]. .It was already shown for n=2. Supposing it is held for D(n−1), the proof is completed by showing D(n)=D×D(n−1). Using j, k, aj(n), R(n) instead of k, m, a0k, R0 of Eq.(3.86) respectively and substituting n−1 for n,
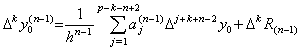 Substituting it for Δky0(n−1) of Eq.(3.75) and using R(1) instead of R0,
Substituting it for Δky0(n−1) of Eq.(3.75) and using R(1) instead of R0,
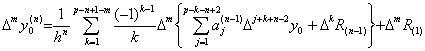 _______(3.88)
Supposing y(p+1)(t)≡0, the terms with ΔkR(n−1), R(1) and R(n) vanish and Eq.(3.88) comes to, _______(3.88)
Supposing y(p+1)(t)≡0, the terms with ΔkR(n−1), R(1) and R(n) vanish and Eq.(3.88) comes to,
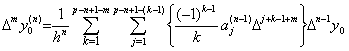 _______(3.89)
There exist the values j and k such as j+k−1+m>p−n+1 and the differences are higher order than Δpy0. The differences are a part of remainder and vanish by the supposition. Replacing j+k−1+m by i and rearranging the other terms by Δi of the order of i=1, 2, 3, ………, in case of m=0, _______(3.89)
There exist the values j and k such as j+k−1+m>p−n+1 and the differences are higher order than Δpy0. The differences are a part of remainder and vanish by the supposition. Replacing j+k−1+m by i and rearranging the other terms by Δi of the order of i=1, 2, 3, ………, in case of m=0,
- If i=1, it must be k=1 and j=1. Hence, the coefficient of Δ is the expression 1) below. It is the product of the first row of D and the first column of D(n−1).
- If i=2, it must be (k=1, j=2) and (k=2, j=1). Hence, the coefficient of Δ2 is the expression 2) below. It is the product of the first row of D and the second column of D(n−1).
- If i=3, it must be (k=1, j=3), (k=2, j=2) and (k=3, j=1). Hence, the coefficient of Δ3 is the expression 3) below. It is the product of the first row of D and the third column of D(n−1).
- In the same way, if i=p−n+1, it must be j=(p−n+1)∼1 for k=1∼(p−n+1). Hence, the coefficient of Δp−n+1 is the expression 4) below. It is the product of the first row of D and the (p−n+1)th column of D(n−1).
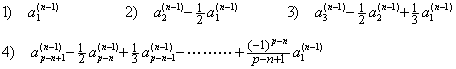 . .
In case of m=1, if i=1, there dose not exists the value of k and j because of j+k=1. Hence, the coefficient of Δ is zero. It is the product of the second row of D and the first column of D(n−1). If i=2, the case of j and k is the first item above and the coefficient of Δ2 is the expression 1) above. It is the product of the second row of D and the second column of D(n−1). If i=3, the case of j and k is the second item above and the coefficient of Δ3 is the expression 2) above. It is the product of the second row of D and the third column of D(n−1). If i=4, the case of j and k is the third item above and the coefficient of Δ4 is the expression 3) above. It is the product of the second row of D and the fourth column of D(n−1). If i=p−n+1, it must be j=(p−n)∼1 for k=1∼(p−n) because of j+k=p−n+1. Hence, the coefficient of Δp−n+1 is the expression below. It is the product of the second row of D and the (p−n+1)th column of D(n−1). . .
In case of m=1, if i=1, there dose not exists the value of k and j because of j+k=1. Hence, the coefficient of Δ is zero. It is the product of the second row of D and the first column of D(n−1). If i=2, the case of j and k is the first item above and the coefficient of Δ2 is the expression 1) above. It is the product of the second row of D and the second column of D(n−1). If i=3, the case of j and k is the second item above and the coefficient of Δ3 is the expression 2) above. It is the product of the second row of D and the third column of D(n−1). If i=4, the case of j and k is the third item above and the coefficient of Δ4 is the expression 3) above. It is the product of the second row of D and the fourth column of D(n−1). If i=p−n+1, it must be j=(p−n)∼1 for k=1∼(p−n) because of j+k=p−n+1. Hence, the coefficient of Δp−n+1 is the expression below. It is the product of the second row of D and the (p−n+1)th column of D(n−1).
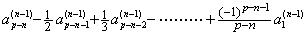 . .
In case of any m such as m≤p−n, if i is less than or equal to m, there dose not exists the value of k and j because of j+k−1+m≤m, that is, j+k≤1. Hence, the coefficient of Δi is zero. It is the product of the (m+1)th row of D and the i-th column of D(n−1). If i=m+1, the case of j and k is the first item above and the coefficient of Δm+1 is expression 1) above. It is the product of the (m+1)th row of D and the (m+1)th column of D(n−1). In the same way, if i=p−n+1, it must be j=(p−n+1−m)∼1 for k=1∼(p−n+1−m) because of j+k=p−n+2−m. Hence, the coefficient of Δp−n+1 is the expression below. It is the product of the (m+1)th row of D and the (p−n+1)th column of D(n−1). . .
In case of any m such as m≤p−n, if i is less than or equal to m, there dose not exists the value of k and j because of j+k−1+m≤m, that is, j+k≤1. Hence, the coefficient of Δi is zero. It is the product of the (m+1)th row of D and the i-th column of D(n−1). If i=m+1, the case of j and k is the first item above and the coefficient of Δm+1 is expression 1) above. It is the product of the (m+1)th row of D and the (m+1)th column of D(n−1). In the same way, if i=p−n+1, it must be j=(p−n+1−m)∼1 for k=1∼(p−n+1−m) because of j+k=p−n+2−m. Hence, the coefficient of Δp−n+1 is the expression below. It is the product of the (m+1)th row of D and the (p−n+1)th column of D(n−1).
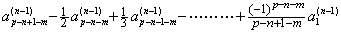 . .
When y(p+1)(t) is not identical with zero, Newton's interpolation formula separates the function y(t) into the two parts which are of the lower order than tp+1 and the remainder. The differentiation does not yield the differences of higher order than Δpy0 in the part of lower order and the remainder vanishes for h→0. Therefore D(n)=D×D(n−1) is always held for the function y(t) such that y(t)∈Cp+1[a, b]. . .
When y(p+1)(t) is not identical with zero, Newton's interpolation formula separates the function y(t) into the two parts which are of the lower order than tp+1 and the remainder. The differentiation does not yield the differences of higher order than Δpy0 in the part of lower order and the remainder vanishes for h→0. Therefore D(n)=D×D(n−1) is always held for the function y(t) such that y(t)∈Cp+1[a, b].
. .
Accordingly, the coefficients of Δi for any m are expressed in Eq. (3.90) in general.
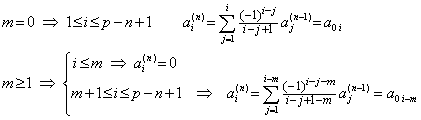 _____(3.90)
Using these coefficients and using k instead of i−m, Eq. (3.89) comes to, _____(3.90)
Using these coefficients and using k instead of i−m, Eq. (3.89) comes to,
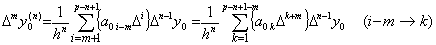 This is equivalent to Eq.(3.86) without remainder term.
This is equivalent to Eq.(3.86) without remainder term.. .
[Theorem 3.27]
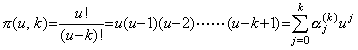 _____(3.91) _____(3.91)
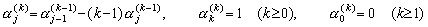 ____(3.92)
(Stirling's numbers of the first kind)
[Proof]. .α0(0)=1 is evident because of π(u,0)=1. If k≥1, ____(3.92)
(Stirling's numbers of the first kind)
[Proof]. .α0(0)=1 is evident because of π(u,0)=1. If k≥1,
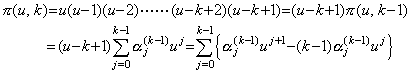 Comparing the coefficient of uk with Eq.(3.91), we obtain
Comparing the coefficient of uk with Eq.(3.91), we obtain
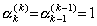 . There does not exist the term with u0 for k≥1. Hence α0(k)=0. For the coefficients of the other uj,
. There does not exist the term with u0 for k≥1. Hence α0(k)=0. For the coefficients of the other uj,
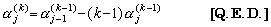
. .
The coefficients of the mid-side of Eq.(3.82) are expressed in Stirling's numbers at t=t0 by Eq. (3.91) as follows, because there exists only the case of j=n for r=0.
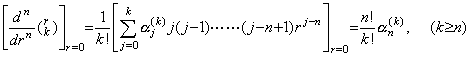 ____(3.93)
It is zero for k<n because there is no term with rj−n for j<n. Accordingly, substituting k+n−1 for k, the new value k becomes k≥1 because of k+n−1≥n and we obtain the coefficients of the rightest side of Eq.(3.82) at m=0. Substituting Eq.(3.92) for it, Theorem 3.23 is obtained as follows. ____(3.93)
It is zero for k<n because there is no term with rj−n for j<n. Accordingly, substituting k+n−1 for k, the new value k becomes k≥1 because of k+n−1≥n and we obtain the coefficients of the rightest side of Eq.(3.82) at m=0. Substituting Eq.(3.92) for it, Theorem 3.23 is obtained as follows.
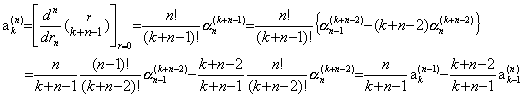 . .
In case of n=1, the value j is j=1 in Eq. (3.93) and Stirling's numbers comes to following expression so Eq.(3.30) is obtained. . .
In case of n=1, the value j is j=1 in Eq. (3.93) and Stirling's numbers comes to following expression so Eq.(3.30) is obtained.
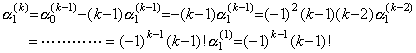 . .
It is not easy to express Stirling's numbers for j>1 in simple formula. However, it is easily computed by use of Table 3.3 as follows. Setting αj(k)=1 for j=k and α0(k)=0 for k≥1, αj(k) is obtained by Eq.(3.92) for j<k. . .
It is not easy to express Stirling's numbers for j>1 in simple formula. However, it is easily computed by use of Table 3.3 as follows. Setting αj(k)=1 for j=k and α0(k)=0 for k≥1, αj(k) is obtained by Eq.(3.92) for j<k.
. .
It is able to compute the first row k-th element of the operator Dn by use of Table 3.3 and Eq.(3.93), where the value j and k are respectively n and k+n−1 of Table 3.2. For example, the coefficient of n=5 and k=6 in Table 3.2 is,
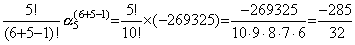

Return to CONTENTS
|
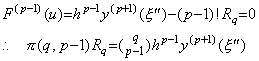
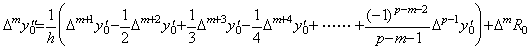
 ___(3.51)
___(3.51)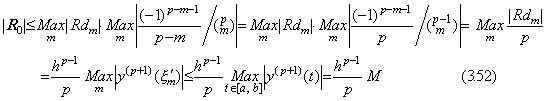
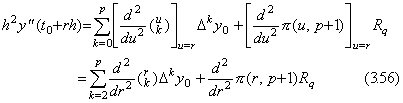
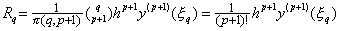 ________[Q.E.D]
________[Q.E.D]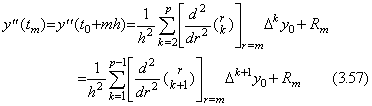
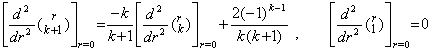 ____(3.58)
____(3.58)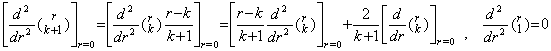
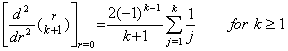 ______(3.60)
______(3.60)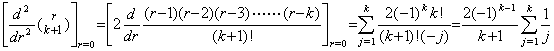
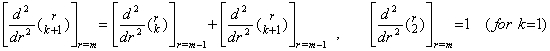 ____(3.61)
____(3.61)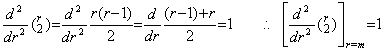
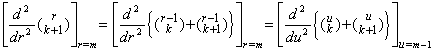
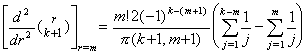 _____(3.62)
_____(3.62)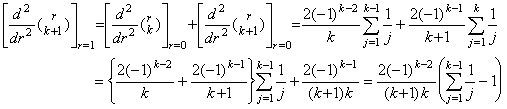
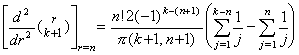
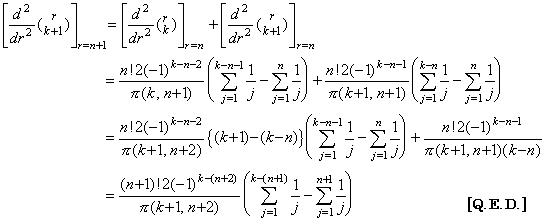
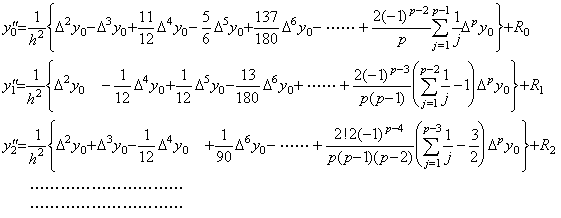
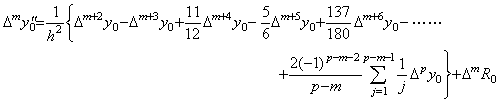 ___(3.63)
___(3.63)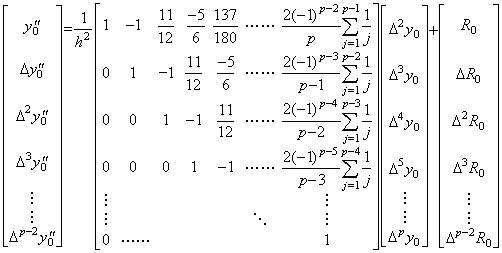 __(3.64)
__(3.64)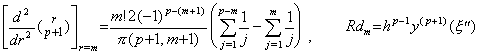
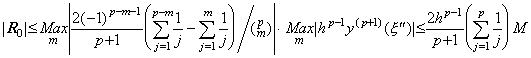
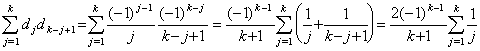 ____(3.66)
____(3.66)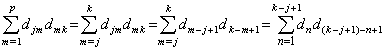
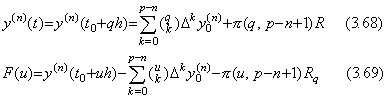
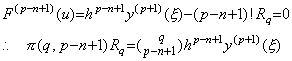
 _____(3.75)
_____(3.75)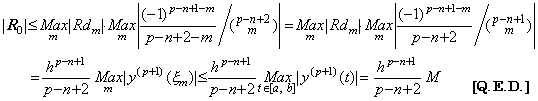
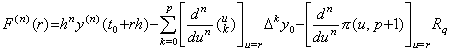 ____(3.81)
____(3.81)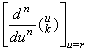 is equivalent to
is equivalent to
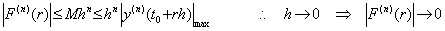 ____[Q.E.D.]
____[Q.E.D.]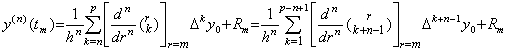 ___(3.82)
___(3.82)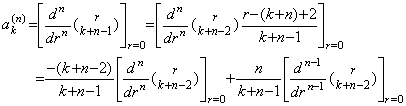
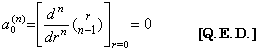


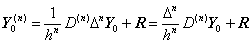 ______(3.87)
______(3.87)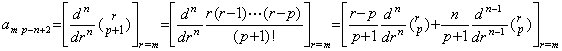
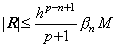 , _____where |y(p+1)(t)|≤M
, _____where |y(p+1)(t)|≤M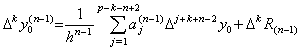
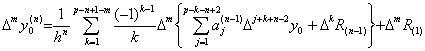 _______(3.88)
_______(3.88)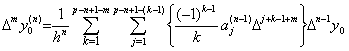 _______(3.89)
_______(3.89)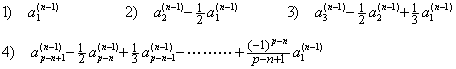
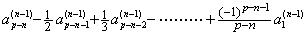
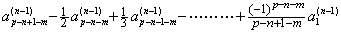
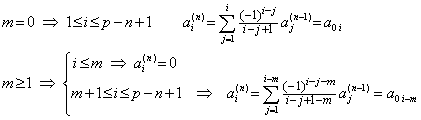 _____(3.90)
_____(3.90)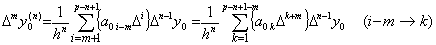
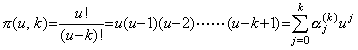 _____(3.91)
_____(3.91)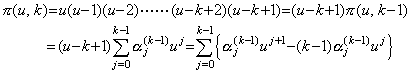
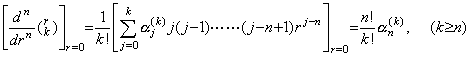 ____(3.93)
____(3.93)