|
5. 演算子空間
5.1 ベクトル空間
. .
数値計算は無理数を持たないがそれに近い有理数及び有理関数を用いて無理数及び無理関数の近似計算を行うことが出来る。本演算子法も無理数及び無理関数に相当するベクトルや演算子を持たないが、それに近いベクトルやベクトル値関数を用いてこれらを扱うことが出来る。又、複素数や複素関数も2つのベクトルの順序対を用いて扱うことが出来る。
. .
ある数 a の平方根は自乗すると a になる数と定義される。同様に、ある関数 y(t) の平方根は自乗すると y(t) になる関数と定義される。その関数を z(t) で表すと、等間隔区分点 t=t0+kh (k=0, 1, 2, ………) における関数値の間には zk2=yk という関係がある。両辺の逐次階差を計算すると、右辺はベクトル Y の要素になり、左辺は関数 z2(t) を表すベクトルの要素になる。後者はベクトルの積 Z×Z の要素に等しい。故に、ベクトル Y の平方根は自乗するとベクトル Y になるベクトルと定義される。このベクトル Z は zk (k=0, 1, 2, ………) の逐次階差を計算して求めてもよい。又、本演算子法を用いた Newton-Raphson 法により得ることも出来る。
. .
関数 y(t) が2次関数のとき、その平方根 z(t) は2次方程式 y(t)=0 の判別式が零の場合を除き Taylor 展開において無限次数の関数になる。従って、そのベクトルの平方根は無限個の要素を持ち、無限次元のベクトル空間にある。そのようなベクトルはベクトル記号を用いた数式で扱うことが出来る。数値計算は要素の数を最初の p 個の要素 z0 から Δp−1z0 迄に切詰めざるを得ない。但し、その他の要素が全て Newton の補間公式の剰余項として無視できるものとする。従って、p の値を全ベクトル中の最大の次元数とすれば全てのベクトルは p 次元距離空間 Rp にある。
. .
次元数の切詰めは距離空間 R∞ のベクトルがその部分空間 Rp へ正射影されることを意味する。何故なら、それは Rp の外側の空間の全ての要素を零にすることと同じであるからである。ベクトル列の軌跡が3次元ユークリッド空間で連続なら、2次元空間への正射影はベクトルの3次元目の要素を零にするだけであり、3次元目の要素が零でないベクトルを取り除くのではないから連続である。同様に、ベクトル列が距離空間 R∞ において連続なら、部分空間 Rp への正射影は連続性を保つ。
. .
著者は第 1.2 節でベクトル Y の大きさを関数 y(t) のノルムで定義した。実数の絶対値は又実数であるように、ベクトルの大きさもまたベクトルであり、与えられた閉区間で |y(t)|≤||y(t)|| である定数関数を表すベクトルである。従って、著者はこの距離空間における二つのベクトル Y と Z の間の距離を関数の差のノルム ||y(t)−z(t)|| を表す定数ベクトルで定義する。本演算子法では定数ベクトルと数値の区別をしないから、ベクトルの大きさ及び距離は理解が煩雑でなければ数値で表してもよい。ベクトルの絶対値の表記 |Y| は関数 |y(t)| を表す。同様に、ベクトルの大きさは ||y(t)|| であるからベクトルのノルム ||Y|| で表す。故に、
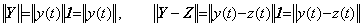 _____(5.1) _____(5.1)
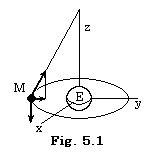 . .
空間 Rp+1 で起こる現象を空間 Rp の現象として観測すると、空間 Rp には実際には存在しない現象があたかも存在するように見える。3次元ユークリッド空間において Fig. 5.1 に示すような振子を考える。重力は x−y 面に垂直とし、振子はその錘が原点の周りを回るように振られているとする。振子の錘を月と呼び、原点にある球体を地球と呼ぶことにする。我々が x−y 平面で表される2次元空間に居るなら、月が地球の周りを回転するのは見えるが振子の紐および重力は見えず、月が地球の周りを回転するのを止めれば月は地球に落ちるのを見る。月と地球は紐で繋がれていないにもかかわらず両者の間には力が働き、それは万有引力が存在するかのように見える。或いは、紐の正射影が両者を繋いでいるのが見えるのかもしれないが、その紐は目には見えるが触ることのできない不思議な紐である。実際には、我々は3次元空間に居てその求心力は振子の紐の張力の x−y 平面への正射影であることが分かる。ここで、2次元空間に居る我々が求めたいものは月 M に働く真の力、即ち、3次元空間の紐に働く張力である。しかし、張力の z 軸成分は x−y 平面に直交しているため見ることができない。x−y 平面の成分からそれを推測することも不可能である。月 M に働く真の力を知るためには3次元空間に出なければならない。 . .
空間 Rp+1 で起こる現象を空間 Rp の現象として観測すると、空間 Rp には実際には存在しない現象があたかも存在するように見える。3次元ユークリッド空間において Fig. 5.1 に示すような振子を考える。重力は x−y 面に垂直とし、振子はその錘が原点の周りを回るように振られているとする。振子の錘を月と呼び、原点にある球体を地球と呼ぶことにする。我々が x−y 平面で表される2次元空間に居るなら、月が地球の周りを回転するのは見えるが振子の紐および重力は見えず、月が地球の周りを回転するのを止めれば月は地球に落ちるのを見る。月と地球は紐で繋がれていないにもかかわらず両者の間には力が働き、それは万有引力が存在するかのように見える。或いは、紐の正射影が両者を繋いでいるのが見えるのかもしれないが、その紐は目には見えるが触ることのできない不思議な紐である。実際には、我々は3次元空間に居てその求心力は振子の紐の張力の x−y 平面への正射影であることが分かる。ここで、2次元空間に居る我々が求めたいものは月 M に働く真の力、即ち、3次元空間の紐に働く張力である。しかし、張力の z 軸成分は x−y 平面に直交しているため見ることができない。x−y 平面の成分からそれを推測することも不可能である。月 M に働く真の力を知るためには3次元空間に出なければならない。
. .
同様の現象が本ベクトル空間においても Newton の補間公式の剰余項により起こる。本演算子法においては、関数は y(t)∈Cp+1[a, b] を満たすことが仮定されている。故に、全てのベクトルは p+1 次元空間に存在し、剰余項はその外側の空間に存在する。空間 R∞ のベクトルを Y で表し、空間 Rp+1 へのその正射影を Z で表すと、剰余項は Y−Z であり、空間 Rp+1 に直交するから空間 Rp+1 へのその正射影は零である。ベクトル Z はベクトル Y の Rp+1 における部分ベクトルであるが、ベクトル Z の表す関数 z(t)はベクトル Y の表す関数 y(t)とは区分点以外では一致せず、剰余項という補正を加える必要があると Newtonの剰余項付補間公式は述べている。剰余項はベクトル Y−Z の要素だけ、即ち、Rp+1 に直交する外の空間にあるベクトル Y の要素で決まる量であり、Rp+1 には実在しない量である。この量は Rp+1 の内部に居ては知ることは不可能であり、この空間の外に出る、即ち、より高次の補間公式と比較すればその量をある程度推測することができる。
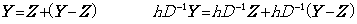 _____(5.1a). .
ベクトル Y に積分演算子を掛けたベクトルとベクトル Z に積分演算子を掛けたベクトルとの関係は(5.1a)で表される。Y−Z は Rp+1 の外のベクトル要素であるから(5.1a)はhD−1Y の Rp+1 の部分ベクトルとhD−1Z とは一致することを表しているように見える。しかし、第4.4節の(4.28)に示した剰余項付積分公式は剰余項 Y−Z に積分演算子を掛けて得られる補正値を加えたものが hD−1Y の Rp+1 の部分ベクトルと一致するのであることを述べている。この補正なしに両者が一致するのは Y=Z の場合、即ち、Y が Rp+1 のベクトルである場合に限られる。このことは微分方程式の数値解を求めるとき、空間 Rp+1 の内部のみで反復修正しても真の解の空間 Rp+1 への正射影に収束するとは限らないことを示す。正しい反復修正は現空間での予測・修正値と少なくとも1次元高次の空間での予測・修正値との差を比較することが必要である。あるいは区分幅を小さくすることでも等価な効果が得られる。Milne法のような予測子修正子法が固定次数の修正子で何度も反復修正するのは剰余項が零の解への収束を求めていることを意味し、剰余項が無視できない場合には真の解から外れていくのは当然であって、解法の安定不安定の問題ではない。 _____(5.1a). .
ベクトル Y に積分演算子を掛けたベクトルとベクトル Z に積分演算子を掛けたベクトルとの関係は(5.1a)で表される。Y−Z は Rp+1 の外のベクトル要素であるから(5.1a)はhD−1Y の Rp+1 の部分ベクトルとhD−1Z とは一致することを表しているように見える。しかし、第4.4節の(4.28)に示した剰余項付積分公式は剰余項 Y−Z に積分演算子を掛けて得られる補正値を加えたものが hD−1Y の Rp+1 の部分ベクトルと一致するのであることを述べている。この補正なしに両者が一致するのは Y=Z の場合、即ち、Y が Rp+1 のベクトルである場合に限られる。このことは微分方程式の数値解を求めるとき、空間 Rp+1 の内部のみで反復修正しても真の解の空間 Rp+1 への正射影に収束するとは限らないことを示す。正しい反復修正は現空間での予測・修正値と少なくとも1次元高次の空間での予測・修正値との差を比較することが必要である。あるいは区分幅を小さくすることでも等価な効果が得られる。Milne法のような予測子修正子法が固定次数の修正子で何度も反復修正するのは剰余項が零の解への収束を求めていることを意味し、剰余項が無視できない場合には真の解から外れていくのは当然であって、解法の安定不安定の問題ではない。
. .
従来、Runge K. 法は安定であるといわれるが、著者の解法と同様に、オイラー法、中点法、シンプソン法と解の近似次数を上げていくから Milne 法よりは安定である。しかし、解法として安定か、不安定かに関する従来の議論は意味がない。両者の比較例として下記(A)の微分方程式の数値解がよく挙げられる。表5.1の(A)欄に Java による区分幅 h=0.1 の単精度計算の解を示す。Java では単精度変数に代入しない限り、途中の計算は二倍長で行われるので BASIC 等よりは多少精度はよくなる。この解は t=7.0 でも有効桁2桁の精度を持っているが、Milne 法では t=5 辺りから暴走を開始する。しかし、Runge K. 法が安定であるといえるのは1階の微分方程式の場合だけである。(A)の微分方程式を微分すると(B)の微分方程式を得るが、表5.1の(B)欄に示すように、t=0.3 辺りから最下位桁の精度が落ち始め、t=5.7 辺りから Milne 法と同じ様な暴走を開始し、t=7.0 では真の解の 1000 倍に達する。(B)の微分方程式を微分すると(C)の微分方程式を得るが、表5.1の(C)欄に示すように、t=0.3 辺りから(B)より更に精度が落ち、t=5.6 辺りでは(B)の解の2倍程の値となり、t=7.0 では真の解の 3000 倍に達する。従来、微分方程式の数値解法は固定次数で十分とする議論は間違っている。
| 表 5.1 Runge K. 法による1, 2, 3 階の微分方程式の解(Java) |
| t | (A) | (B) | (C) | 10exp(−t2/2) |
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
:
:
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
6.0
:
:
7.0 |
10.0
9.950125
9.801987
9.559975
9.231163
8.824968
8.352701
7.8270445
7.26149
6.669768
6.0653067
:
:
1.3491768E-5
7.985243E-6
4.679384E-6
2.7150177E-6
1.5597049E-6
8.871567E-7
4.996307E-7
2.786066E-7
1.5382618E-7
:
:
2.3525334E-10 |
10.0
9.950125
9.801988
9.559977
9.231166
8.824973
8.352707
7.827051
7.261497
6.669775
6.0653133
:
:
1.31268E-5
7.6325705E-6
4.33697E-6
2.381408E-6
1.2338529E-6
5.683E-7
1.8720138E-7
-2.7829543E-8
-1.4696013E-7
:
:
-2.5513947E-7 |
10.0
9.950125
9.801988
9.5599785
9.231171
8.82498
8.352717
7.8270645
7.2615128
6.669793
6.0653334
:
:
1.4252864E-5
8.749632E-6
5.4440843E-6
3.4780796E-6
2.3198932E-6
1.6437227E-6
1.2521507E-6
1.02687E-6
8.977589E-7
:
:
7.0546184E-7 |
10.0
9.950124790
9.801986727
9.559974784
9.231163442
8.824969026
8.352701995
7.827045448
7.261490301
6.669767894
6.065306597
:
:
1.343810278E-5
7.949385579E-6
4.655713318E-6
2.699578503E-6
1.549753963E-6
8.808164832E-7
4.956399836E-7
2.761240903E-7
1.522997974E-7
:
:
2.289734846E-10 |
. .
Milne 法等の従来の予測子・修正子法は二つの誤りを犯している。一つは固定次数の固定区分幅解法で修正子を反復すれば正しい解に収束するという考え、もう一つは予測子より修正子の次数が低いことである。これでは予測子で得た精度を修正子で落としていることになる。ただ、異なる次数の近似積分式の結果を比較するという点だけは正しいが、それ以後の修正子の反復は意味がない。
5.2 演算子値とノルムに関する諸問題
. .
通常の微分及び積分演算において、その定義は変数 t が変化しても被演算関数が変わっても変わらない。これは被演算関数に対して演算結果の関数を対応させる法則が、被演算関数が変わっても変わらないのであるから、演算子値は一定値であることを意味する。関数 f(t)は独立変数 t に対して f という法則を作用させる対応である。例えば、三次関数 t3 場合は、f は3個の t を掛けるという法則であるが、t に t2 を掛けるという法則でもある。何れにせよ、掛ける量が独立変数 t の変化に従って変化するから、この法則は独立変数 t により変化する。定数関数は独立変数 t に対して常にある定数を対応させるものであり、この法則は独立変数 t が変化しても変化しない。微積分演算子が被演算関数に演算結果の関数を対応させる法則はこれと同様の関係にあり、演算子の違いは法則、即ち、定義の違いであるから関数の違いに相当し、それぞれの演算子は、その定義が独立変数に相当する被演算関数が変わっても変化しないのであるから、定数関数に相当する。従って、それぞれの演算子の違いは定数関数の定数の違いに相当する。従来、抽象的にのみ終始する議論では、積分演算子は上に有界であるが、微分演算子は上に有界でないとされるが、全く意味がないと考えられる。
. .
被演算関数が atn, (n≠−1)の場合には積分演算子は次のように一次関数に等価である。
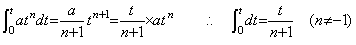 _____(5.2)
従来の微積分演算における演算子の考えでは、この関数を積分演算子の演算子値と考えることが出来る。この演算子値は被演算関数の n の値が変わらないなら積分の上限が何処にあっても変わらない。従って、この演算子値を掛けることにより t0 から t 迄の積分を求めることも可能である。 _____(5.2)
従来の微積分演算における演算子の考えでは、この関数を積分演算子の演算子値と考えることが出来る。この演算子値は被演算関数の n の値が変わらないなら積分の上限が何処にあっても変わらない。従って、この演算子値を掛けることにより t0 から t 迄の積分を求めることも可能である。
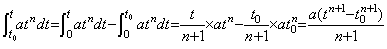 ____(5.3)
n の値が変わると演算子値は変わるように見える。しかし、勾配は異なるが一次関数であることに変わりはない。故に、文字が傾斜していても同じものであるのと同様に演算子値は勾配が変わっても同じ値である。演算子は一定値の演算子値を持つけれども、被演算関数に応じてその係数を変える。係数が変わっても積分の定義は変わらないから、この係数の違いは演算子値の違いではない。この点が演算子の関数との違いである。 ____(5.3)
n の値が変わると演算子値は変わるように見える。しかし、勾配は異なるが一次関数であることに変わりはない。故に、文字が傾斜していても同じものであるのと同様に演算子値は勾配が変わっても同じ値である。演算子は一定値の演算子値を持つけれども、被演算関数に応じてその係数を変える。係数が変わっても積分の定義は変わらないから、この係数の違いは演算子値の違いではない。この点が演算子の関数との違いである。
. .
n の値が演算子値の違いを表すとすると、n の値が −1 に漸近するなら演算子値は無限大になり、積分演算子のノルムは存在しないことになる。n の値が演算子値に無関係であるから n=0 のときの関数 t が積分演算子値であるとするのが正しい。この演算子値は被演算関数が変わっても変化しないから積分演算子値のノルムも関数 t である。積分の上限が負の場合も考慮に入れるなら、被演算関数のノルムとの積が負にならないためには関数 |t| が積分演算子のノルムとなる。実数の絶対値が実数であるように、演算子値のノルムもまた演算子値である。
. .
演算子法は演算子値が一定値であることを明示的に示す。Laplace 変換及び Mikusinski の演算子法は二つの関数の積を畳込み積分で定義する。従って、積分演算子の演算子値は畳込み積分が被積分関数の積分となるような関数である。この関数は Laplace 変換では s−1 で表される。即ち、それはユニットステップ関数 u(t) である。この演算子値は被積分関数が変わっても変わらない、即ち、一定値である。この積を記号 * で表し、第2章3節で定義したインパルス関数及びユニットステップ関数を用いると、
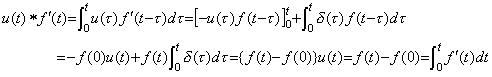 __(5.4)
関数及び導関数が f(t)u(t) 及び f '(t)u(t) で表される場合には、t の値は積分の上限であるから被積分関数において u(t)=1 を用いれば、 __(5.4)
関数及び導関数が f(t)u(t) 及び f '(t)u(t) で表される場合には、t の値は積分の上限であるから被積分関数において u(t)=1 を用いれば、
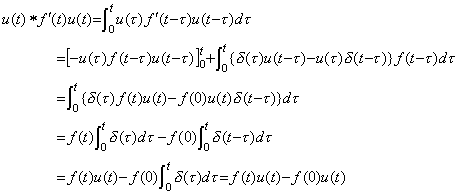 __(5.5)
これは f '(t)u(t) の積分に等しい。何故なら、 __(5.5)
これは f '(t)u(t) の積分に等しい。何故なら、
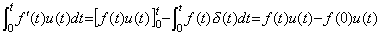 _____(5.6)
Mikusinski は関数 f(t)u(t) 及び f '(t)u(t) を、{f(t)}, {f '(t)} と表し、積分演算子の演算子値、即ち、ユニットステップ関数を {1} で表す。 _____(5.6)
Mikusinski は関数 f(t)u(t) 及び f '(t)u(t) を、{f(t)}, {f '(t)} と表し、積分演算子の演算子値、即ち、ユニットステップ関数を {1} で表す。
. .
この演算子値のノルムは又ユニットステップ関数である。何故なら、
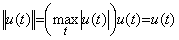 ________(5.7)
演算子値のノルムと被演算子のノルムの積も畳込み積分で行われねばならない。 ________(5.7)
演算子値のノルムと被演算子のノルムの積も畳込み積分で行われねばならない。
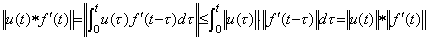 ____(5.8)
従って、このノルムの積を通常の積で表すと、積分演算子のノルムは次に示すように関数 t となる。 ____(5.8)
従って、このノルムの積を通常の積で表すと、積分演算子のノルムは次に示すように関数 t となる。
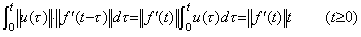 _____(5.9). .
第2章 1.5 節の定理 1.1 において著者は区間が [t, t+h] であるとき積分演算子のノルムは h であることを示した。従来の積分演算においても、区間が [t0, t] なら次の定理が成立する。しかし、これは積分演算子値が変化することを意味するものではない。積分の定義はその下限から上限までを積分するのであるから、下限が移動すれば演算子もその位置に移動しなければならない。従って、積分演算子値である関数 t が関数 t−t0 にシフトされただけで演算子値が変わったのではない。 _____(5.9). .
第2章 1.5 節の定理 1.1 において著者は区間が [t, t+h] であるとき積分演算子のノルムは h であることを示した。従来の積分演算においても、区間が [t0, t] なら次の定理が成立する。しかし、これは積分演算子値が変化することを意味するものではない。積分の定義はその下限から上限までを積分するのであるから、下限が移動すれば演算子もその位置に移動しなければならない。従って、積分演算子値である関数 t が関数 t−t0 にシフトされただけで演算子値が変わったのではない。
. .
[定理 5.1]. .積分区間が t0 から t 迄なら積分演算子のノルムは関数 |t−t0| である。
[証明]. .t>t0 とすると、
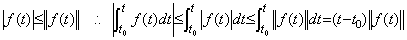 ____(5.10)
t<t0 の場合は、 ____(5.10)
t<t0 の場合は、
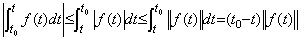 _____(5.11)
関数 f(t) が定数なら全ての等号が成立する。______________________[Q.E.D.] _____(5.11)
関数 f(t) が定数なら全ての等号が成立する。______________________[Q.E.D.]
. .
n の値が −1 以外なら負でも整数でなくても(5.2)は成立するが、−1 に近づくなら、(5.2)の一次関数の係数は無限大に近づく。これらの場合は、関数 atn を f(t) で表すと、この関数は t0≠0 に対して剰余項付きの Taylor 展開で表される。
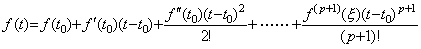 ____(5.12)
この右辺の各項を積分する積分演算子の演算子値は 0 以上 p+1 迄の整数を分母に持つ一次関数で表される。故に、(5.2)の演算子値は n の値として零以上の整数だけを持つ一次関数を考えればよい。これも n の値が演算子値の違いを意味するものでないことを示す。 ____(5.12)
この右辺の各項を積分する積分演算子の演算子値は 0 以上 p+1 迄の整数を分母に持つ一次関数で表される。故に、(5.2)の演算子値は n の値として零以上の整数だけを持つ一次関数を考えればよい。これも n の値が演算子値の違いを意味するものでないことを示す。
. .
(5.2)の積分演算の被積分関数を一般的に atn, (n≠−1)で表したのであるから、その逆演算である微分演算の被微分関数は一般的に bt(n+1) で表すことが出来る。この場合の微分演算及びその演算子値は次のように表される。
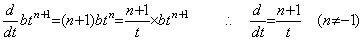 _____(5.13)
或る n の値を持つ積分演算子の逆演算子は同じ n の値を持つ(5.13)の微分演算子であり、両者の積は必ず1になる。従来、微分演算子を作用させた後に積分演算子を作用させる場合は両者の積は1にならないとされているが、積分演算子を積分と初期値加算の合成演算と考えている重大な間違いによるものである。積分演算子は初期値加算演算を含まない演算で、積分結果は y(t)−y0 になるというのが正しい。従って、微分演算の被演算関数は従来 y(t) とされているのも間違いであり、y(t)−y0 でなければならない。積分演算子値が n の値に無関係な一定値であるから、微分演算子値も n の値に無関係な一定値であり、n=0 のときの関数 1/t である。そのノルムも関数 1/t であるが、t が負のとき被微分関数のノルムとの積が負にならないためには関数 |1/t| が微分演算子のノルムである。従って、両者のノルムの積も次の関係を満たす。 _____(5.13)
或る n の値を持つ積分演算子の逆演算子は同じ n の値を持つ(5.13)の微分演算子であり、両者の積は必ず1になる。従来、微分演算子を作用させた後に積分演算子を作用させる場合は両者の積は1にならないとされているが、積分演算子を積分と初期値加算の合成演算と考えている重大な間違いによるものである。積分演算子は初期値加算演算を含まない演算で、積分結果は y(t)−y0 になるというのが正しい。従って、微分演算の被演算関数は従来 y(t) とされているのも間違いであり、y(t)−y0 でなければならない。積分演算子値が n の値に無関係な一定値であるから、微分演算子値も n の値に無関係な一定値であり、n=0 のときの関数 1/t である。そのノルムも関数 1/t であるが、t が負のとき被微分関数のノルムとの積が負にならないためには関数 |1/t| が微分演算子のノルムである。従って、両者のノルムの積も次の関係を満たす。
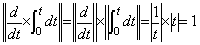 ______(5.14). .
演算子を T で表すと、T が積分演算子なら次の関係が成立する。 ______(5.14). .
演算子を T で表すと、T が積分演算子なら次の関係が成立する。
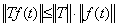 ______(5.15)
しかし、微分演算子の場合は成立しない。(5.15)の f(t) を導関数 f '(t) に替えて積分結果 Tf '(t) を f(t)−f0 で表すと(5.16)の関係が得られる。この式は従来の議論に於いて微分演算子が上に有界でない根拠とされているようであるが、それは間違いである。微分演算子値が上に有界でないということは微分の定義が無限に存在することであり、定義が変わらない事実に矛盾する。 (5.16)は、導関数の最大絶対値は微分演算子のノルムと被微分関数のノルムの積以上になると述べているに過ぎない。導関数にノルムが存在しない場合でも、(5.16)の導関数 f '(t) のノルムを無限大に置き換えた不等号は成立する。従来、微分演算子は上に有界でないとしている議論は誤りである。 ______(5.15)
しかし、微分演算子の場合は成立しない。(5.15)の f(t) を導関数 f '(t) に替えて積分結果 Tf '(t) を f(t)−f0 で表すと(5.16)の関係が得られる。この式は従来の議論に於いて微分演算子が上に有界でない根拠とされているようであるが、それは間違いである。微分演算子値が上に有界でないということは微分の定義が無限に存在することであり、定義が変わらない事実に矛盾する。 (5.16)は、導関数の最大絶対値は微分演算子のノルムと被微分関数のノルムの積以上になると述べているに過ぎない。導関数にノルムが存在しない場合でも、(5.16)の導関数 f '(t) のノルムを無限大に置き換えた不等号は成立する。従来、微分演算子は上に有界でないとしている議論は誤りである。
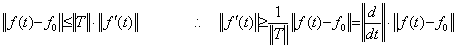 _____(5.16). .
Laplace 変換は微分演算子を s で表す。これは Dirac のデルタ関数ではなく、第2章 3.2 節で定義したインパルス関数 δ(t) の導関数である。この畳込み積分は次のようになる。 _____(5.16). .
Laplace 変換は微分演算子を s で表す。これは Dirac のデルタ関数ではなく、第2章 3.2 節で定義したインパルス関数 δ(t) の導関数である。この畳込み積分は次のようになる。
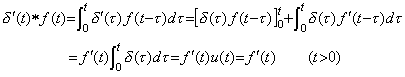 ____(5.17)
f(t)u(t) 及び f '(t)u(t) で表される関数及びその導関数の場合には、t は積分の上限であるから被積分関数において u(t)=1 及び δ(t)=0 を用いると、 ____(5.17)
f(t)u(t) 及び f '(t)u(t) で表される関数及びその導関数の場合には、t は積分の上限であるから被積分関数において u(t)=1 及び δ(t)=0 を用いると、
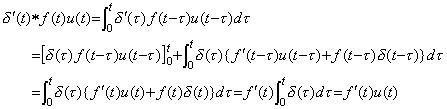 ___(5.18). .
従って、微分演算子値は被演算関数が何であっても関数 δ' (t) である、即ち、一定値である。第2章 3.9 節の定理 3.7 を用いると、u(t) と δ' (t) の積、即ち、畳込み積分は次のようになる。 ___(5.18). .
従って、微分演算子値は被演算関数が何であっても関数 δ' (t) である、即ち、一定値である。第2章 3.9 節の定理 3.7 を用いると、u(t) と δ' (t) の積、即ち、畳込み積分は次のようになる。
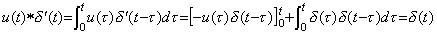 ___(5.19)
インパルス関数は恒等演算を意味する。何故なら、 ___(5.19)
インパルス関数は恒等演算を意味する。何故なら、
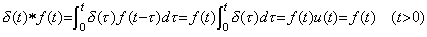 ____(5.20) ____(5.20)
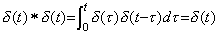 ______(5.21)
Mikusinski はそれを数値演算子 1 で表す。関数としては δ' (t) は t=+0 において +∞ から −∞ 迄変わり、δ(t) は t=+0 において 0 から +∞ 迄変わるけれども、微分演算子値及び恒等演算子値は演算子値として正の一定値である。何故なら、畳込み積分は u(t) 及び f(t) の符号を変えないからである。故に、 ______(5.21)
Mikusinski はそれを数値演算子 1 で表す。関数としては δ' (t) は t=+0 において +∞ から −∞ 迄変わり、δ(t) は t=+0 において 0 から +∞ 迄変わるけれども、微分演算子値及び恒等演算子値は演算子値として正の一定値である。何故なら、畳込み積分は u(t) 及び f(t) の符号を変えないからである。故に、
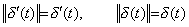 ________(5.22) ________(5.22)
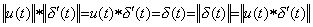 ____(5.23)
これらの畳込み積分としての積を通常の積に変換すると、恒等演算子及び微分演算子のノルムは次のようにそれぞれ1及び 1/t となる。 ____(5.23)
これらの畳込み積分としての積を通常の積に変換すると、恒等演算子及び微分演算子のノルムは次のようにそれぞれ1及び 1/t となる。
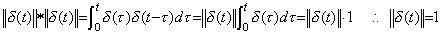 ___(5.24) ___(5.24)
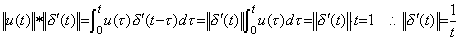 ___(5.25)
被演算関数により定義が変わらない演算子の演算子値は被演算関数に対して変化しない一定値であり、演算子のノルムもその演算子値に同じであるから、二つの演算子の積とそのノルムに関する(5.15)に相当する関係式は不等号は必要なく等号のみが成立する。 ___(5.25)
被演算関数により定義が変わらない演算子の演算子値は被演算関数に対して変化しない一定値であり、演算子のノルムもその演算子値に同じであるから、二つの演算子の積とそのノルムに関する(5.15)に相当する関係式は不等号は必要なく等号のみが成立する。
. .
演算子を T で表し、関数 f(t) を Maclaurin 展開で表すと、
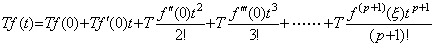 ___(5.26)
T が積分演算子なら、右辺の n+1 番目の T は t/(n+1)に等価であるが、分配則が成立しているのであるから、n=0, 1, 2, 3, ………に対するこれら T の値は演算子値として全て同じである。従来の議論では、左辺の被積分関数 f(t)が変更されると演算子値が変わると考えられているが、変化するのは演算子値ではなく Maclaurin 展開の係数 f(n)(0)である。従って、積分演算子値は一定値、即ち、関数 t であり、そのノルムも関数 t である。T が微分演算子なら、右辺の n+1 番目の T は n/t に等価であるが、積分演算子の場合と同様に、これらの値は演算子値として全て同じであり、被微分関数 f(t)が変更されても変わらない。従って、微分演算子値は一定値、即ち、関数 1/t であり、そのノルムも関数 1/t である。 ___(5.26)
T が積分演算子なら、右辺の n+1 番目の T は t/(n+1)に等価であるが、分配則が成立しているのであるから、n=0, 1, 2, 3, ………に対するこれら T の値は演算子値として全て同じである。従来の議論では、左辺の被積分関数 f(t)が変更されると演算子値が変わると考えられているが、変化するのは演算子値ではなく Maclaurin 展開の係数 f(n)(0)である。従って、積分演算子値は一定値、即ち、関数 t であり、そのノルムも関数 t である。T が微分演算子なら、右辺の n+1 番目の T は n/t に等価であるが、積分演算子の場合と同様に、これらの値は演算子値として全て同じであり、被微分関数 f(t)が変更されても変わらない。従って、微分演算子値は一定値、即ち、関数 1/t であり、そのノルムも関数 1/t である。
. .
ベクトルの概念を用いれば演算子値とそのノルムの間のこれらの関係を理解することは容易である。Maclaurin 展開で表された(5.26)の関数 f(t) を縦ベクトルで表し、余白の節約のため( )を用いて横方向にあらわすと、
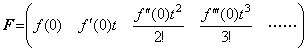 ____(5.27)
T が積分演算子なら(5.26)は次のように表される。 ____(5.27)
T が積分演算子なら(5.26)は次のように表される。
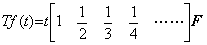 ____(5.28)
T が微分演算子なら(5.26)は(5.29)のように表される。L_shiftは(5.27)のベクトルFからf(0)を取除き、全要素を1要素左へ移す演算子である。 ____(5.28)
T が微分演算子なら(5.26)は(5.29)のように表される。L_shiftは(5.27)のベクトルFからf(0)を取除き、全要素を1要素左へ移す演算子である。
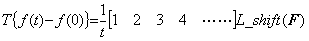 _____(5.29)
横ベクトルで表されたこれらの演算子値は被演算関数 F が変更されても変わらない。即ち、演算子値は一定値である。被積分関数が f(t)=atn なら、n=0 のとき(5.30)の1番目の要素であるから、ベクトル F は n+1 番目の要素だけが零でない。 _____(5.29)
横ベクトルで表されたこれらの演算子値は被演算関数 F が変更されても変わらない。即ち、演算子値は一定値である。被積分関数が f(t)=atn なら、n=0 のとき(5.30)の1番目の要素であるから、ベクトル F は n+1 番目の要素だけが零でない。
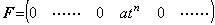 _____(5.30)
従って、積分演算子ベクトルとの積を演算した結果は、(5.2)に示したように積分演算子は(5.28)の n+1 番目の要素の値を持つかのように見えるのである。この積分結果は f(t)−f0 であるから btn+1 であり、(5.30)の1要素右の n+2 番目だけが零でない。L_shiftの演算により n+1 番目の要素だけが零でないから、(5.13)に示したように逆演算の微分演算子は(5.29)の n+1 番目の要素の値を持つかのように見えるのである。これが n の値が演算子値として意味を持たない理由である。故に、ベクトル演算(5.28)(5.29)の演算子ベクトルの値は n=0 である第1要素の値であり、積分演算子値はベクトルt、微分演算子値はベクトル1/tである。 _____(5.30)
従って、積分演算子ベクトルとの積を演算した結果は、(5.2)に示したように積分演算子は(5.28)の n+1 番目の要素の値を持つかのように見えるのである。この積分結果は f(t)−f0 であるから btn+1 であり、(5.30)の1要素右の n+2 番目だけが零でない。L_shiftの演算により n+1 番目の要素だけが零でないから、(5.13)に示したように逆演算の微分演算子は(5.29)の n+1 番目の要素の値を持つかのように見えるのである。これが n の値が演算子値として意味を持たない理由である。故に、ベクトル演算(5.28)(5.29)の演算子ベクトルの値は n=0 である第1要素の値であり、積分演算子値はベクトルt、微分演算子値はベクトル1/tである。
. .
関数 f(t) のノルムは又次のような第一要素のみが零でないベクトルで表される関数である。
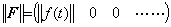 ____(5.31)
故に、T が積分演算子なら、 ____(5.31)
故に、T が積分演算子なら、
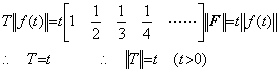 ____(5.32)
従って、(5.28)の横ベクトルは積分演算子値及びそのノルムに無関係であり、これも(5.2)の n の値がノルムに関して意味を持たない理由である。又、|F|≤||F|| であるから、 ____(5.32)
従って、(5.28)の横ベクトルは積分演算子値及びそのノルムに無関係であり、これも(5.2)の n の値がノルムに関して意味を持たない理由である。又、|F|≤||F|| であるから、
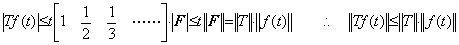 ___(5.33)
. .
演算子 T が微分演算子のときは、(5.29)のベクトルF を ||F|| に替えると T||F||=0 となり、(5.32)に相当する演算が出来ないので微分演算子値もノルムも直接求めることは出来ない。通常の微分演算のときも、被微分関数が定数関数 ||f(t)|| ならその初期値も ||f(t)|| であるから、初期値を減算した結果は零となるので微分結果は得られない。微分演算子のノルムが得られない原因は、関数のノルムの概念が微分結果のノルムを与えるための全ての性質を失ってしまうことにある。微分演算子のノルムは(5.32)に示した関数のノルム ||f(t)|| の積分結果 T||f(t)|| を微分することにより得なければならない。T||f(t)|| は t の一次関数だからベクトルで表すと(5.34)で表される。 ___(5.33)
. .
演算子 T が微分演算子のときは、(5.29)のベクトルF を ||F|| に替えると T||F||=0 となり、(5.32)に相当する演算が出来ないので微分演算子値もノルムも直接求めることは出来ない。通常の微分演算のときも、被微分関数が定数関数 ||f(t)|| ならその初期値も ||f(t)|| であるから、初期値を減算した結果は零となるので微分結果は得られない。微分演算子のノルムが得られない原因は、関数のノルムの概念が微分結果のノルムを与えるための全ての性質を失ってしまうことにある。微分演算子のノルムは(5.32)に示した関数のノルム ||f(t)|| の積分結果 T||f(t)|| を微分することにより得なければならない。T||f(t)|| は t の一次関数だからベクトルで表すと(5.34)で表される。
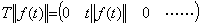 ____(5.34)
(5.29)の微分演算子をDで表し、T||f(t)||を微分すると、 ____(5.34)
(5.29)の微分演算子をDで表し、T||f(t)||を微分すると、
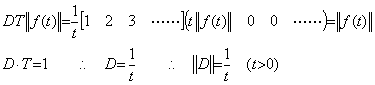 _____(5.35)
(5.33)の被積分関数をf '(t)に替えると、 _____(5.35)
(5.33)の被積分関数をf '(t)に替えると、
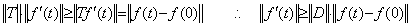 _____(5.36). .
(5.28)の積分演算子をベクトル T で表し、(5.29)の微分演算子をベクトル D で表すと、両演算子の積は右側のベクトルを縦ベクトルに変換して行わなければならない。(5.30)の説明で示したように、ベクトル T の n+1 番目の要素が作用する積分演算の逆演算はベクトル D の n+1 番目の要素が作用するから、ベクトル T とベクトル D との積の結果のベクトル要素は全て 1 になる。これは両演算子の演算順序を逆にしても同じである。従来の微積分における考え方では逆順の場合は恒等変換でないといわれるが、この考え方は間違っている。既に述べているように、被微分関数は f(t)−f(0)であり、これを微分した導関数を逆に積分した結果も f(t)−f(0)である。従来は、これに初期値 f(0)を加えたものを逆演算の積分結果としているが、これは積分と初期値加算の合成演算であって積分演算ではない。また、導関数に存在しない積分結果の初期値を積分演算の被演算子とすること自体が間違いである。両演算子の積は恒等変換演算子としてベクトル(5.37)で表される。 _____(5.36). .
(5.28)の積分演算子をベクトル T で表し、(5.29)の微分演算子をベクトル D で表すと、両演算子の積は右側のベクトルを縦ベクトルに変換して行わなければならない。(5.30)の説明で示したように、ベクトル T の n+1 番目の要素が作用する積分演算の逆演算はベクトル D の n+1 番目の要素が作用するから、ベクトル T とベクトル D との積の結果のベクトル要素は全て 1 になる。これは両演算子の演算順序を逆にしても同じである。従来の微積分における考え方では逆順の場合は恒等変換でないといわれるが、この考え方は間違っている。既に述べているように、被微分関数は f(t)−f(0)であり、これを微分した導関数を逆に積分した結果も f(t)−f(0)である。従来は、これに初期値 f(0)を加えたものを逆演算の積分結果としているが、これは積分と初期値加算の合成演算であって積分演算ではない。また、導関数に存在しない積分結果の初期値を積分演算の被演算子とすること自体が間違いである。両演算子の積は恒等変換演算子としてベクトル(5.37)で表される。
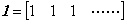 ________(5.37). .
微分演算子ベクトル D と積分演算子ベクトル T は共に関数ベクトル F に対しては横ベクトルであるが、両演算子の積の場合は右の演算子を縦ベクトルに変換しなければならない原因は演算子と関数ベクトルの積の結果を関数ベクトルで表していないことにある。結果を関数ベクトルで表せばこれらの積は行列演算で表され、Maclaurin展開またはTaylor展開に基づくもう一つの演算子法が導かれる。 ________(5.37). .
微分演算子ベクトル D と積分演算子ベクトル T は共に関数ベクトル F に対しては横ベクトルであるが、両演算子の積の場合は右の演算子を縦ベクトルに変換しなければならない原因は演算子と関数ベクトルの積の結果を関数ベクトルで表していないことにある。結果を関数ベクトルで表せばこれらの積は行列演算で表され、Maclaurin展開またはTaylor展開に基づくもう一つの演算子法が導かれる。
. .
(5.26)の関数 f(t)を関数 y(t)の導関数とすると、(5.26)の左辺は、演算子 T が積分演算子なら y(t)−y(0)になる。この左辺を Maclaurin 展開で表すと、
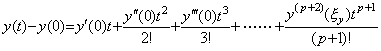 ____(5.38)
この右辺の各項は(5.26)のそれぞれに対応する項に等しい。従って、f(t) 及び y(t)−y(0) を(5.27)に述べたベクトルで表すと、積分演算は次の行列演算で表される。 ____(5.38)
この右辺の各項は(5.26)のそれぞれに対応する項に等しい。従って、f(t) 及び y(t)−y(0) を(5.27)に述べたベクトルで表すと、積分演算は次の行列演算で表される。
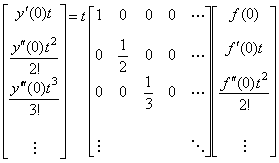 _____(5.39)
(5.26)の各項を左辺に置けば、微分演算は次のよう表される。 _____(5.39)
(5.26)の各項を左辺に置けば、微分演算は次のよう表される。
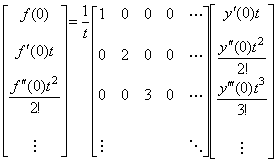 _____(5.40)
この二つの演算子の積は順序に関係なく単位行列、即ち、恒等演算子になる。 _____(5.40)
この二つの演算子の積は順序に関係なく単位行列、即ち、恒等演算子になる。
. .
二つの関数 f(t) 及び g(t) の積を逐次に微分すると、
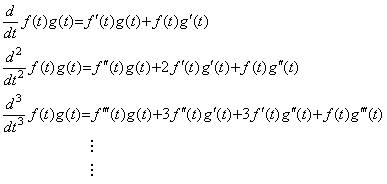 ____(5.41)
従って、積 f(t)g(t) の Maclaurin 展開を f(t) 及び g(t) の Maclaurin 展開の積で表すと、関数を表す二つのベクトルの積は行列演算で表される。 ____(5.41)
従って、積 f(t)g(t) の Maclaurin 展開を f(t) 及び g(t) の Maclaurin 展開の積で表すと、関数を表す二つのベクトルの積は行列演算で表される。
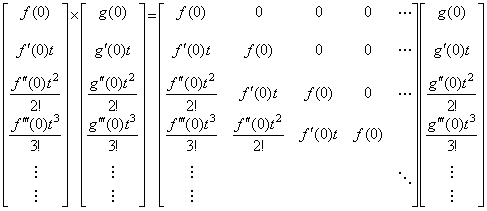 ___(5.42)
この行列はベクトルに等価な演算子である。著者はこれをベクトルの行列、即ち、演算子への展開と呼ぶ。二つのベクトルの積は、左のベクトルを演算子に換えて積の演算を行う必要があるが、整数に小数点をつけて実数に変換するのと同様に、表記形式の変換であってノルム等ベクトルの特性に変化を与えるものではない。Laplace 変換及び Mikusinski の演算子法は二つの関数の積を畳込み積分で定義したのと同様に、これは二つのベクトルの積の定義である。従って、微積分演算子とベクトルの積の場合も微積分演算子を行列に展開しなければならない。積分演算子は関数 t であるが、行列展開すると(5.39)の積分演算子で表され、微分演算子は関数 1/t であるが、行列展開すると(5.40)の微分演算子で表されるのであり、展開された行列は演算子のノルムに影響しない。両演算子は対角要素以外の要素は全て零であり、対角要素は同じ値ではなく、これらの演算子はベクトルの行列への展開とは異なるものである。逐次階差に基づく著者の演算子法の微積分演算子の行列もこれとまったく同様である。 ___(5.42)
この行列はベクトルに等価な演算子である。著者はこれをベクトルの行列、即ち、演算子への展開と呼ぶ。二つのベクトルの積は、左のベクトルを演算子に換えて積の演算を行う必要があるが、整数に小数点をつけて実数に変換するのと同様に、表記形式の変換であってノルム等ベクトルの特性に変化を与えるものではない。Laplace 変換及び Mikusinski の演算子法は二つの関数の積を畳込み積分で定義したのと同様に、これは二つのベクトルの積の定義である。従って、微積分演算子とベクトルの積の場合も微積分演算子を行列に展開しなければならない。積分演算子は関数 t であるが、行列展開すると(5.39)の積分演算子で表され、微分演算子は関数 1/t であるが、行列展開すると(5.40)の微分演算子で表されるのであり、展開された行列は演算子のノルムに影響しない。両演算子は対角要素以外の要素は全て零であり、対角要素は同じ値ではなく、これらの演算子はベクトルの行列への展開とは異なるものである。逐次階差に基づく著者の演算子法の微積分演算子の行列もこれとまったく同様である。
5.3 通常の微積分における演算子のノルムの定義
. .
前節の(5.2)に示した被積分関数 at n, (n≠−1)の積分の仕方は平均値の定理に基づいていると考えることができる。この関数の 0 から t までの積分の平均値を与える点を ξ とすると、その平均値は aξ n であるから積分値は aξ nt となる。ξ n は n=0 なら 1、n=1 なら中間点 t/2、n=2 以降(5.43)に示すようになる。従って、(5.2)に示した n+1 を分母に持つ一次関数は、関数 t と被積分関数を任意の t 迄の平均値に変換する演算子との積である。
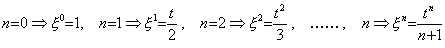 _______(5.43). .
この被積分関数を任意の t 迄の平均値に変換する演算子は、被積分関数の次数 n が変われば変わるように見える。しかし、(5.26)の Maclaurin 展開の積分で分配則が成立することを見れば、この平均値に変換する演算子は演算子値としては全て同じであると考えなければならない。演算子値として n の値が無関係であるから、この変換演算子の演算子値は 1 であると考えなければならない。従って、積分演算子の演算子値は関数 t である。 _______(5.43). .
この被積分関数を任意の t 迄の平均値に変換する演算子は、被積分関数の次数 n が変われば変わるように見える。しかし、(5.26)の Maclaurin 展開の積分で分配則が成立することを見れば、この平均値に変換する演算子は演算子値としては全て同じであると考えなければならない。演算子値として n の値が無関係であるから、この変換演算子の演算子値は 1 であると考えなければならない。従って、積分演算子の演算子値は関数 t である。
. .
(5.28)に大括弧で示したベクトル表記の考えを取り入れると、この平均値に変換する演算子は 1/(n+1)で計算される全ての値を要素とする集合であり、被積分関数 at n, (n≠−1)の n の値に応じてその要素の一つが作用すると考えることが出来る。この集合は一つしかないのであるから(5.26)の右辺の積分演算子 T は全て同じであり、分配則が成立する。又、左辺の積分演算子 T と右辺の積分演算子 T は n が何でも同じであるから、演算子としてのこの集合の値は n=0 の要素の値 1 でなければならず、そのノルムも 1 である。従って、積分演算子の演算子値は関数 t であり、そのノルムも関数 t である。
. .
関数 at n, (n≠−1)の積分結果は一般的に bt (n+1) で表すことが出来る。この逆演算である微分演算は(5.13)で表されるが、積分結果が平均値に t を掛けたものであるから、その逆演算は 1/t を掛けて平均値 aξ n を得た後、n+1 を掛けて関数 at n, に変換すると考えることが出来る。(5.43)から、(n+1)ξ n は n の値に対して(5.44)に示すようになる。従って、(5.13)の微分演算子の分子の n+1 は平均値を関数に変換する演算子である。
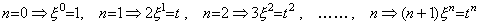 _________(5.44). .
積分演算子の場合と同様に、この平均値を関数に変換する演算子は n+1 で計算される値を要素とする集合であり、被微分関数 bt (n+1) の n の値に応じてその一つの要素が作用する。Maclaurin 展開の微分演算、即ち、(5.26)の演算子 T が微分演算子の場合も分配則の成立する理由であり、この平均値を関数に変換する演算子の値は集合としての値 1 でなければならず、そのノルムも 1 である。従って、微分演算子の値には何の影響もなく、微分演算子の値は関数 1/t であり、そのノルムも関数 1/t である。 _________(5.44). .
積分演算子の場合と同様に、この平均値を関数に変換する演算子は n+1 で計算される値を要素とする集合であり、被微分関数 bt (n+1) の n の値に応じてその一つの要素が作用する。Maclaurin 展開の微分演算、即ち、(5.26)の演算子 T が微分演算子の場合も分配則の成立する理由であり、この平均値を関数に変換する演算子の値は集合としての値 1 でなければならず、そのノルムも 1 である。従って、微分演算子の値には何の影響もなく、微分演算子の値は関数 1/t であり、そのノルムも関数 1/t である。
. .
関数を平均値に変換する演算子も、逆に平均値を関数に変換する演算子もその値及びノルムが 1 であるということは両変換とも等価変換であり、(5.42)に示したベクトルの行列展開と同様に、被演算関数の性質に何の変化も与えないことを意味する。又、両者の集合の同じ n に対する要素は逆数の関係にあるから、集合は関数を平均値に変換するもの一つとし、微分演算の場合はその要素の逆数が作用すると考えることも出来る。Maclaurin 展開の微積分を行列演算で表した(5.39)及び(5.40)に含まれる行列もこれらと同じ意味を持っている。著者の演算子法の微積分演算子の行列もまた同様である。. .
[定義 5.1]. .関数 f(t)を t=0 から任意の t 迄積分した平均値を与える点をξ t とすると、平均値は t の関数 f(ξ t)で表される。この関数を f(t)の平均関数と呼ぶ。. .
上記の議論を一般的な関数の微積分演算に拡張する。関数 y(t)の導関数を f(t)で表すと、積分演算は平均関数 f(ξ t)を用いて次のように表される。
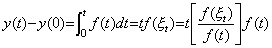 _________(5.45)
大括弧で示したのが関数を平均値に変換する演算子である。この演算子は、あらゆる積分可能な関数について、関数 f(t)とその平均関数 f(ξ t)の対を要素とする集合である。そして、被積分関数に一致する関数 f(t)及びその平均関数 f(ξ t)の対の要素が(5.45)に基づいて作用する。(5.43)の場合は、被積分関数が at n であり、その平均関数が at n/(n+1)であるから、この対の要素が平均値変換に作用する値は 1/(n+1)となったのである。この場合の演算子、即ち、集合のノルムは被積分関数とその平均関数が同じであるときの要素の値であった。同様に、(5.45)の関数を平均関数に変換する演算子、即ち、集合のノルムも関数 f(t)とその平均関数f (ξ t)が同じである要素の与える値 1 である。この演算子は一つしかなく、そのノルムが 1 であるからこの演算子の演算子値も 1 である。従って、被積分関数 f(t)とその平均関数 f(ξ t)とは等価である。故に、積分演算子値は関数 t であり、そのノルムも関数 t である。. .
[定義 5.2]. .あらゆる積分可能な関数 f(t)とその平均関数 f(ξ t)の対を要素とする集合を平均関数変換演算子と呼ぶ。この演算子は、被積分関数に一致する関数 f(t)を持つ要素が関数 f(t)を分母とし、その平均関数 f(ξ t)を分子として作用する。 _________(5.45)
大括弧で示したのが関数を平均値に変換する演算子である。この演算子は、あらゆる積分可能な関数について、関数 f(t)とその平均関数 f(ξ t)の対を要素とする集合である。そして、被積分関数に一致する関数 f(t)及びその平均関数 f(ξ t)の対の要素が(5.45)に基づいて作用する。(5.43)の場合は、被積分関数が at n であり、その平均関数が at n/(n+1)であるから、この対の要素が平均値変換に作用する値は 1/(n+1)となったのである。この場合の演算子、即ち、集合のノルムは被積分関数とその平均関数が同じであるときの要素の値であった。同様に、(5.45)の関数を平均関数に変換する演算子、即ち、集合のノルムも関数 f(t)とその平均関数f (ξ t)が同じである要素の与える値 1 である。この演算子は一つしかなく、そのノルムが 1 であるからこの演算子の演算子値も 1 である。従って、被積分関数 f(t)とその平均関数 f(ξ t)とは等価である。故に、積分演算子値は関数 t であり、そのノルムも関数 t である。. .
[定義 5.2]. .あらゆる積分可能な関数 f(t)とその平均関数 f(ξ t)の対を要素とする集合を平均関数変換演算子と呼ぶ。この演算子は、被積分関数に一致する関数 f(t)を持つ要素が関数 f(t)を分母とし、その平均関数 f(ξ t)を分子として作用する。. .
任意の関数 y(t)を微分する場合は(5.45)より次のように表される。
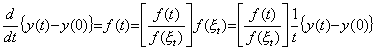 ________(5.46)
従って、微分演算は被微分関数 y(t)−y(0)を t で除した関数(微分の平均値 f(ξ t))に、積分演算の平均関数変換演算子の平均関数 f(ξ t)を対の一方とする要素が積分の場合の逆数で作用する演算である。従って、この変換演算子は平均関数 f(ξ t)を関数 f(t)に変換する演算子で、平均関数変換演算子の逆演算子である。平均関数変換演算子の演算子値及びノルムは 1 であるから、この逆変換演算子の値もノルムも 1 である。故に、微分演算子の演算子値もノルムも関数 1/t である。. .
[定義 5.3]. .微分の場合は、平均関数変換演算子が逆演算子として作用し、平均関数変換の場合と逆に、被微分関数を t で除した関数(微分の平均値)に一致する平均関数 f(ξ t)を持つ要素が関数 f(t)を分子とし、その平均関数 f(ξ t)を分母として作用する。 ________(5.46)
従って、微分演算は被微分関数 y(t)−y(0)を t で除した関数(微分の平均値 f(ξ t))に、積分演算の平均関数変換演算子の平均関数 f(ξ t)を対の一方とする要素が積分の場合の逆数で作用する演算である。従って、この変換演算子は平均関数 f(ξ t)を関数 f(t)に変換する演算子で、平均関数変換演算子の逆演算子である。平均関数変換演算子の演算子値及びノルムは 1 であるから、この逆変換演算子の値もノルムも 1 である。故に、微分演算子の演算子値もノルムも関数 1/t である。. .
[定義 5.3]. .微分の場合は、平均関数変換演算子が逆演算子として作用し、平均関数変換の場合と逆に、被微分関数を t で除した関数(微分の平均値)に一致する平均関数 f(ξ t)を持つ要素が関数 f(t)を分子とし、その平均関数 f(ξ t)を分母として作用する。. .
微積分演算にこのような特殊な演算子の付加を考えなければならない原因は、微積分演算を抽象的に線形演算として関数との四則演算の積で扱おうという具体性を無視した抽象的議論にある。Laplace 変換及び Mikusinski の演算子法では二つの関数の積を畳込み積分で定義することにより、微積分演算を演算子と被演算関数の積で実現することが出来たのである。通常の積分演算を演算子と被演算関数の四則演算の積で実行できるのは被演算関数が定数関数の場合だけであり、微分演算の場合は被演算関数が一次関数の場合だけである。一般的な被演算関数に対しては、既に述べたように、積分演算の場合は被演算関数を平均関数に変換する演算子が必要であり、微分演算の場合は微分結果の平均関数を関数に変換する演算子、即ち、逆演算子が必要である。これ等の演算子は関数に作用するものであり、微積分演算子に作用するものではない。Laplace 変換及び Mikusinski の演算子法と同様に、これ等の演算子により微積分演算子と被演算関数の積を定義するという方法も可能である。積の演算子は値を持たないが、敢えて演算子値を持つとするならその値は 1 であり、ノルムも 1 でなければならない。 . .
[定義 5.4]. .平均関数変換演算子を * で表し、この演算子により積分演算子と被積分関数の積を定義する。従って、積分演算は(5.47)、微分演算は(5.48)で表される。但し、演算子 *−1 は 1/t を作用した後で作用する。
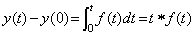 _______(5.47) _______(5.47)
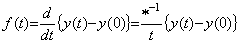 ____(5.48) ____(5.48)
. .
従来、微分演算子は上に有界でないといわれるが実現可能でない抽象的な議論によるもので意味がない。微分演算子が上に有界でない例として次の例がよく示される。(5.49)の関数 y(t)はノルムが零に収束するから関数 y(t)も零に収束する。しかし、関数 y(t)を微分すると、(5.50)に示すように導関数のノルムは 1 に収束し、導関数は零に収束しない。この原因は微分演算子が上に有界でないからであるというものである。
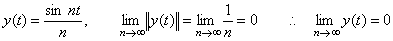 ____(5.49) ____(5.49)
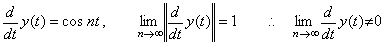 _____(5.50). .
線形演算子を T で表すと、Ty(t)=0 が成立するのは y(t)=0 なる関数の場合に限られる。従って、limy(t)=0 なら limTy(t)=Tlimy(t)=0 とならなければならないが、微分演算子は上に有界でないから lim 演算子との順序を入れ替えることが出来ないので(5.50)になるという主張である。しかし、この議論は大きな間違いを犯している。結論から言えば、微分演算子と lim 演算子の順序を入れ替えなければならないのである。(5.49)の y(t)を微分するには(5.51)に示すように変数変換するが、ここで変数 f による微分を実行すると(5.50)になる。しかし、n→∞ のとき df→∞ であるからこの微分は不可能である。単純に分子と分母の比を求めれば(5.51)に示すように(5.49)の y(t)の微分の極限は零になる。 _____(5.50). .
線形演算子を T で表すと、Ty(t)=0 が成立するのは y(t)=0 なる関数の場合に限られる。従って、limy(t)=0 なら limTy(t)=Tlimy(t)=0 とならなければならないが、微分演算子は上に有界でないから lim 演算子との順序を入れ替えることが出来ないので(5.50)になるという主張である。しかし、この議論は大きな間違いを犯している。結論から言えば、微分演算子と lim 演算子の順序を入れ替えなければならないのである。(5.49)の y(t)を微分するには(5.51)に示すように変数変換するが、ここで変数 f による微分を実行すると(5.50)になる。しかし、n→∞ のとき df→∞ であるからこの微分は不可能である。単純に分子と分母の比を求めれば(5.51)に示すように(5.49)の y(t)の微分の極限は零になる。
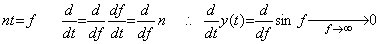 _____(5.51). .
微分の定義に基づいてこの y(t)を微分すると、(5.52)に示すように、n が有限の値のときは h→0 で cos nt に収束するが、n→∞ では nh→0 が必要であり、これは成立しないのである。(5.50)は n を有限な値として先に h→0 としたもので、nh→0 が成立すると断定していることに同じであり間違いである。先に、n→∞とすれば(5.52)の極限は零である。 _____(5.51). .
微分の定義に基づいてこの y(t)を微分すると、(5.52)に示すように、n が有限の値のときは h→0 で cos nt に収束するが、n→∞ では nh→0 が必要であり、これは成立しないのである。(5.50)は n を有限な値として先に h→0 としたもので、nh→0 が成立すると断定していることに同じであり間違いである。先に、n→∞とすれば(5.52)の極限は零である。
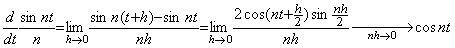 _____(5.52). .
定義 5.4 の平均関数変換演算子を用いてこの y(t)を微分すると、(5.53)に示すように、n が有限な値なら平均関数はcos ξ となり、これを積分の平均値とする関数は cos nt である。しかし、n→∞ では平均関数は恒等的に零であるから、これを積分の平均値とする関数も恒等的に零である。以上から(5.50)の微分演算子とlim演算子の順序は入れ替えなければならない。従って、微分演算子は上に有界であるという結論になる。 _____(5.52). .
定義 5.4 の平均関数変換演算子を用いてこの y(t)を微分すると、(5.53)に示すように、n が有限な値なら平均関数はcos ξ となり、これを積分の平均値とする関数は cos nt である。しかし、n→∞ では平均関数は恒等的に零であるから、これを積分の平均値とする関数も恒等的に零である。以上から(5.50)の微分演算子とlim演算子の順序は入れ替えなければならない。従って、微分演算子は上に有界であるという結論になる。
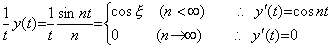 ____(5.53). .
(5.54)の関数 y(t)の微分も微分演算子が上に有界でない例として挙げられる。関数 y(t)は上に有界であるが、導関数 f(t)は t→0 で無限大になり有界でない。これは微分演算子が上に有界でないからであるという。この議論も大きな誤りを犯している。導関数 f(t)は t→0 で無限大になるが、区間[0, t]の積分の平均値 f(ξ)が関数 f(t)より大きな値として常に存在する。積分の平均値 f(ξ)は、t を掛ければ関数 y(t)になるから上に有界である。従って、導関数 f(t)は上に有界であり、微分演算子も上に有界である。 ____(5.53). .
(5.54)の関数 y(t)の微分も微分演算子が上に有界でない例として挙げられる。関数 y(t)は上に有界であるが、導関数 f(t)は t→0 で無限大になり有界でない。これは微分演算子が上に有界でないからであるという。この議論も大きな誤りを犯している。導関数 f(t)は t→0 で無限大になるが、区間[0, t]の積分の平均値 f(ξ)が関数 f(t)より大きな値として常に存在する。積分の平均値 f(ξ)は、t を掛ければ関数 y(t)になるから上に有界である。従って、導関数 f(t)は上に有界であり、微分演算子も上に有界である。
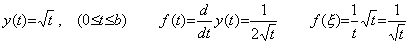 ____(5.54). .
Laplace 変換でよく使われるユニットステップ関数 u(t)はノルムが 1 であり、上に有界であるが、これを微分すると、著者が第2章3.2節で定義したインパルス関数 δ(t)となり、t→0 では δ(t)→∞となる。しかし、この点で導関数は δ'(t)=0 となるので、インパルス関数 δ(t)はこの点でピークを持つ。従って、このピークより大きな有限な値が必ず存在し、インパルス関数は上に有界である。これ等の例は無限大になるというだけで上に有界でないと単純に断定することは出来ないことを示す。インパルス関数 δ(t)は δ(+0)=∞といえるほど大きな値を一点で持つ他は全ての点で零である。このノルムを δ(+0)で定義するのは余にも過大な評価である。前節で述べたように、インパルス関数 δ(t)のノルムは δ(t)で定義して必要にして十分である。その導関数 δ'(t)及びユニットステップ関数 u(t)も同様である。演算子値としての関数のノルムも同様に次のように定義できる。. .
[定義 5.5]. .被演算関数に関わらず同じに定義される演算の演算子としての値である関数は一つであり、ノルムもその関数である。但し、それが被演算関数の符号を変える場合はその関数の絶対値である。 ____(5.54). .
Laplace 変換でよく使われるユニットステップ関数 u(t)はノルムが 1 であり、上に有界であるが、これを微分すると、著者が第2章3.2節で定義したインパルス関数 δ(t)となり、t→0 では δ(t)→∞となる。しかし、この点で導関数は δ'(t)=0 となるので、インパルス関数 δ(t)はこの点でピークを持つ。従って、このピークより大きな有限な値が必ず存在し、インパルス関数は上に有界である。これ等の例は無限大になるというだけで上に有界でないと単純に断定することは出来ないことを示す。インパルス関数 δ(t)は δ(+0)=∞といえるほど大きな値を一点で持つ他は全ての点で零である。このノルムを δ(+0)で定義するのは余にも過大な評価である。前節で述べたように、インパルス関数 δ(t)のノルムは δ(t)で定義して必要にして十分である。その導関数 δ'(t)及びユニットステップ関数 u(t)も同様である。演算子値としての関数のノルムも同様に次のように定義できる。. .
[定義 5.5]. .被演算関数に関わらず同じに定義される演算の演算子としての値である関数は一つであり、ノルムもその関数である。但し、それが被演算関数の符号を変える場合はその関数の絶対値である。
. .
関数 f(t)の t=x における値はこの点にピーク f(x)を持つインパルス関数であり、(5.55)の左辺の被積分関数で表される。−∞<x<∞の全ての点におけるこのようなインパルス関数を全て重ね合わせた、即ち、x により積分したものが関数 f(t)である。この積分は関数 f(t)とインパルス関数の畳込み積分であり、インパルス関数が恒等変換演算子であることからも明らかである。関数 f(t)のノルムはこれらインパルス関数の集合としての大きさである。関数 f(t)の最大絶対値をピークとするインパルス関数は全ての点のインパルス関数以上の大きさを持つが、そのピーク点以外の全ての点では零であり、全てのインパルス関数より小さく、集合の大きさを表すといえない。それら全ての点に、最大のインパルス関数を配置した集合が集合としての大きさ、即ち、ノルムである。それら全てのインパルス関数を重ね合わせると(5.55)と同様にして関数 f(t)の最大絶対値を関数値とする定数関数となる。従って、関数 f(t)のノルムは最大絶対値で定義される。
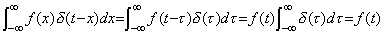 _____(5.55). .
(5.54)の関数 y(t)は連続関数であるが導関数 f(t)は不連続関数であり、これも微分演算子が上に有界でないからであるといわれる。y(t)を微分の定義に基づいて微分すると(5.56)のようになる。従って、t=0 の値は f(t)の積分の平均値であり、導関数 f(t)は t=0 では定義されない。関数 y(t)の t=0 における値は零であるから、f(t)の積分の平均値は無限大であるが上に有界であり、これに零を掛けた値が初期値 y(0)=0 である。しかし、導関数 f(t)は t=0 では定義されないのに積分の平均値が導関数 f(ξ)で定義されるのは矛盾である。従って、関数 y(t)は t=0 では定義できないのであり、不連続関数である。従来、零の平方根は零であるから関数 y(t)は t=0 でも定義されていると単純に考えていることが間違いである。 _____(5.55). .
(5.54)の関数 y(t)は連続関数であるが導関数 f(t)は不連続関数であり、これも微分演算子が上に有界でないからであるといわれる。y(t)を微分の定義に基づいて微分すると(5.56)のようになる。従って、t=0 の値は f(t)の積分の平均値であり、導関数 f(t)は t=0 では定義されない。関数 y(t)の t=0 における値は零であるから、f(t)の積分の平均値は無限大であるが上に有界であり、これに零を掛けた値が初期値 y(0)=0 である。しかし、導関数 f(t)は t=0 では定義されないのに積分の平均値が導関数 f(ξ)で定義されるのは矛盾である。従って、関数 y(t)は t=0 では定義できないのであり、不連続関数である。従来、零の平方根は零であるから関数 y(t)は t=0 でも定義されていると単純に考えていることが間違いである。
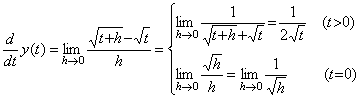 _____(5.56). .
関数 y(t)が t=0 では定義されていないと微分演算の被演算関数が初期値を引いたものであることに問題が生ずると考えるかもしれない。しかし、区間[ε, t]を考えれば、次に示すように微分も積分も何ら問題を生じない。しかし、連続微分可能に関する考え方は変えなければならない。 _____(5.56). .
関数 y(t)が t=0 では定義されていないと微分演算の被演算関数が初期値を引いたものであることに問題が生ずると考えるかもしれない。しかし、区間[ε, t]を考えれば、次に示すように微分も積分も何ら問題を生じない。しかし、連続微分可能に関する考え方は変えなければならない。
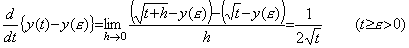 _____(5.57) _____(5.57)
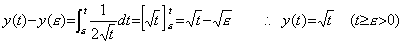 ________(5.58). .
従来、連続微分可能関数の空間に関して(5.59)の関係があるといわれている。この議論も微分のことだけを考慮し、微分演算子は上に有界でないという主張に不都合なため、積分のことは一切考慮していない一方的な議論である。 ________(5.58). .
従来、連続微分可能関数の空間に関して(5.59)の関係があるといわれている。この議論も微分のことだけを考慮し、微分演算子は上に有界でないという主張に不都合なため、積分のことは一切考慮していない一方的な議論である。
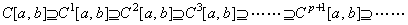 _____(5.59). .
[定理 5.2]_____ _____(5.59). .
[定理 5.2]_____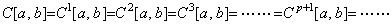 ______(5.60) ______(5.60)
[証明]. .微分可能関数は、微分すると不連続関数になるものと連続関数であるものに分けられるという考えに従えば(5.59)が成立する。一方、C[a, b]の関数を適当な積分定数を与えて積分すれば、それらは全て 1 回連続微分可能関数である。更に、積分定数を変えた関数も全て 1 回連続微分可能関数である。故に、C[a, b]⊆C1[a, b]である。C1[a, b]の関数を同様に積分すれば全て 2 回連続微分可能関数になり、C1[a, b]⊆C2[a, b]である。同様にして(5.61)が成立する。故に、(5.60)でなければならない。
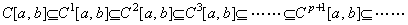 ______(5.61)______[Q.E.D.] ______(5.61)______[Q.E.D.]. .
この定理は、連続関数は無限に連続微分可能であることを示している。一次関数は 2 回微分すると恒等的に零になるが、恒等的に零である関数は微分すると恒等的に零の関数になり、無限に連続微分可能である。(5.54)の関数 y(t)は(5.56)に示したように t=0 で関数の特性である微係数が定義できない。然るに、その点で関数が定義されているとする従来の考えがおかしい。この点では関数値が定義されていない、即ち、不連続関数であるから微分したものも不連続関数なのであり、連続関数が微分により不連続になったのではない。従来の連続関数の定義の問題点については次節に述べる。
5.4 連続関数に関する従来の定義の諸問題
. .
(5.54)の関数 y(t)は t の平方根であることだけを考えれば t=0 で y(t)=0 であり、t≥0 で y(t)は連続であるように見える。従来はこのように考えられている。しかし、微係数を考慮に入れると前節に述べたようにこの考えはおかしい。矢野健太郎編の数学小辞典には連続関数の項に、途中の記述は省略してあるが、次のように二通りに記述されている。
. .[連続関数]. .実数のある開区間で定義され、実数値をとる関数 f(x)が、その区間内の 1 点 a において、条件(5.62)を満たすとき、f(x)は x=a で連続であるという。そして、開区間内の全ての点で連続ならば、関数はその開区間において連続であるという。・・・・・
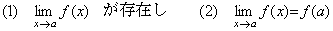 ______(5.62)
・・・関数 f(x)が x=a で連続であるということは次のように述べることができる。即ち、
「任意の正の数 ε をとるとき、それに応じて適当な正の数 δ を選び、|x−a|<δ なる全ての x に対して |f(x)−f(a)|<ε とすることができるならば、f(x)は x=a において連続である。」 ______(5.62)
・・・関数 f(x)が x=a で連続であるということは次のように述べることができる。即ち、
「任意の正の数 ε をとるとき、それに応じて適当な正の数 δ を選び、|x−a|<δ なる全ての x に対して |f(x)−f(a)|<ε とすることができるならば、f(x)は x=a において連続である。」
. .
この前半の定義と後半の定義は同じではないのである。前半の定義の条件(5.62)によれば(5.54)の関数 y(t)は t=0 で連続となるが、後半の定義によれば不連続となる。(5.63)に示すように、|f(x)−f(a)| と |x−a| の比、即ち、微分の平均値の絶対値を k とおくと、kδ の最大値は ε でなければならない。k は x により変わり、x=a では微係数の絶対値になるから、微係数が存在しなくては後半の定義の条件は満たされない。従って、連続であるためには x=a における微係数の存在が必須であり、前半の定義はこの条件を欠いているのである。
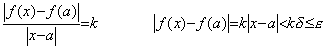 ______(5.63) ______(5.63)
. .
(5.54)の関数 y(t) は t の平方根であるから t→0 では y(t)→0 であるが、y'(0)=∞ であるから t と 0 の距離で測った y(t) と 0 の距離は次第に増加して無限大になる。これは y(t) が 0 に近づく速度が次第に遅くなり、t が +0 から 0 になるとき y(t) が y(+0) から 0 になる速度は零になることを示す。即ち、y(t) は零にはなれないのであり、(5.62)の(2)の条件は満たされないとするのが正しいのである。従来、零の平方根は零であるとする考えに間違いがあり、零の平方根は存在しないのである。t の平方根の定義は y(t)×y(t)=t であるから t>0 なら y(t)=t/y(t) であるが、t=0 のときは 0×0=0 であるが 0=0/0 は成立しない。1次方程式 0×x=0 の解は x=0 ではない。2次方程式 x2=0 の解が x=0 なのは同じものを掛けて零になるのはその場合だけだからで,零の平方根が零だからではない。何故なら,x=0/x は認められない。零は零の平方根としての要件を満たしていないのである。. .
[定理 5.3]. .関数 f(t)が連続関数ならその不定積分は連続関数である。
[証明]. .任意の連続関数を f(t)で表し、任意の積分定数 C を与えて積分すると、関数 y(t)は(5.64)に示すように不定積分で表される。
 ______(5.64). .
関数y(t)は(5.65)の第1式に示すように、任意の t=a において(5.62)の連続の条件を満たしている。(5.65)の第2式に示すように(5.63)の条件も満たしている。 ______(5.64). .
関数y(t)は(5.65)の第1式に示すように、任意の t=a において(5.62)の連続の条件を満たしている。(5.65)の第2式に示すように(5.63)の条件も満たしている。
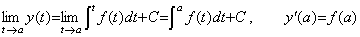 ______(5.65)______[Q.E.D.] ______(5.65)______[Q.E.D.]
. .
この定理は前節の[定理 5.2]の証明の後半(5.61)を補足するものである。これを逆演算で述べれば、導関数 f(t)が連続関数なら被微分関数 y(t)は連続関数であるとなる。又、被微分関数 y(t)が連続関数でないなら導関数 f(t)は連続関数でない。
. .
[定理 5.4]. .導関数 f(t)が連続関数でないなら被微分関数 y(t)は連続関数でない、即ち、被微分関数 y(t)が連続関数なら導関数 f(t)は連続関数である。
[証明]. .関数 y(t)は連続関数であるから上記[連続関数]の後半の定義により任意の t に対して y(t+h)→y(t)であり、微係数 y'(t)が存在する。(y(t), y'(t))の対を考えると、h→0 のとき(y(t+h), y'(t+h))→(y(t), y'(t))であるから、導関数 f(t)=y'(t)は連続の条件(5.62)を満たす。従って、任意の h に対する区間[t−h, t]及び[t, t+h]の微分の平均値の最大絶対値をそれぞれ k1, k2 とすれば、任意の正の数 ε をとるとき、それに応じて適当な正の数 δ を選び、h<δ なる全ての h に対して(5.66)が成立するようにできる。
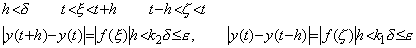 ______(5.66)
このとき、h より小なる全ての |ξ−t|, |ζ−t| に対して f(t)の連続の条件(5.67)が成立する為には、k1, k2, 2k3 の最大のものを k と表せば、kδ≤ε が成立するように δ を選べばよい。 ______(5.66)
このとき、h より小なる全ての |ξ−t|, |ζ−t| に対して f(t)の連続の条件(5.67)が成立する為には、k1, k2, 2k3 の最大のものを k と表せば、kδ≤ε が成立するように δ を選べばよい。
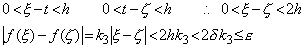 ______(5.67)
h→0 のとき ξ→t, ζ→t であるから、任意の t において f(t)は連続である。______[Q.E.D.] ______(5.67)
h→0 のとき ξ→t, ζ→t であるから、任意の t において f(t)は連続である。______[Q.E.D.]
. .
上記の二つの定理は連続関数と連続微分可能関数の空間は恒等空間であること、即ち、前節[定理 5.2]の別証明である。従来、異なる関数を接続した関数は連続関数であるとされるが、この議論はおかしい。異なる二つの関数を t=1 で接続した(5.68)(A)の関数 y(t)は、接続点でも条件(5.62)を満たし、連続関数であると従来は言われている。しかし、微分すると(B)の関数 f(t)となり、接続点で f(t−0)=2, f(t)=1 であるから関数 f(t)は不連続である。従って、(A)の関数 y(t)も不連続関数である、即ち、異なる微係数で接続された関数は不連続関数である。
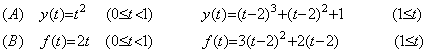 ______(5.68). .
(5.68)(A)の関数を任意の積分定数 C を与えて積分すると(5.69)の関数になる。これ等の関数は全て t=1 において微係数 1 で滑らかに接続していて、連続の条件(5.63)を満たしている。しかし、その導関数(5.68)(A)が不連続関数であるから、これ等の関数は連続の条件(5.63)を満たしていても不連続関数である。(5.69)のどちらかの区間の定数 C をこれと異なる定数 D に替えると、それらの関数は t=1 における値が異なるから明白に不連続関数である。それにもかかわらず、その導関数は(5.68)(A)になる。連続関数の導関数と不連続関数の導関数とが同じ連続関数であるのは不合理である。この意味においても(5.69)の関数は不連続関数であり、異なる二つ以上の関数を接続した関数は接続点の微係数が同じでも不連続関数である。 ______(5.68). .
(5.68)(A)の関数を任意の積分定数 C を与えて積分すると(5.69)の関数になる。これ等の関数は全て t=1 において微係数 1 で滑らかに接続していて、連続の条件(5.63)を満たしている。しかし、その導関数(5.68)(A)が不連続関数であるから、これ等の関数は連続の条件(5.63)を満たしていても不連続関数である。(5.69)のどちらかの区間の定数 C をこれと異なる定数 D に替えると、それらの関数は t=1 における値が異なるから明白に不連続関数である。それにもかかわらず、その導関数は(5.68)(A)になる。連続関数の導関数と不連続関数の導関数とが同じ連続関数であるのは不合理である。この意味においても(5.69)の関数は不連続関数であり、異なる二つ以上の関数を接続した関数は接続点の微係数が同じでも不連続関数である。
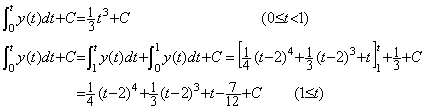 ______(5.69). .
従来、上記のような独立変数が一つの関数は2次元空間に存在するとされている。しかし、第1節で述べたことと同様に、実際は3次元空間の関数を2次元空間で眺めているのであり、そのため上記のような奇妙な現象が見られるのであるということができる。独立変数 t と関数値 y との関係を表す2次元平面の原点(0, 0)においてこの面に直交する第三の座標軸は関数 y(t)の定数項の値を表す。この座標軸を定数項軸と呼ぶことにする。(5.69)の区間(0≤t<1)の関数は定数項軸の C 点においてこの軸に直交する2次元平面にある関数である。区間(1≤t)の関数は定数項軸の y(0)=C+3/4 の点においてこの軸に直交する2次元平面にある関数の(1≤t)の部分である。従って、(5.69)の関数はこの3次元空間においては接続していない。微分演算が定数項に無関係なのは、関数 y(t)の t 軸方向の編微分を求める演算であり、定数項軸方向の微分には無関係だからである。被微分関数は定数項を減算するのも同じ意味であり、微分結果はその定数項の位置にある2次元平面に移動する。逆に、積分演算はその結果の関数が存在する2次元平面の位置を定めなければならないから積分定数を必要とする。従来の議論はこの3次元空間の全ての2次元平面を定数項軸の原点にある2次元平面に重ねて眺めているから(5.68)(A)や(5.69)の関数は接続しているように見えるのである。 ______(5.69). .
従来、上記のような独立変数が一つの関数は2次元空間に存在するとされている。しかし、第1節で述べたことと同様に、実際は3次元空間の関数を2次元空間で眺めているのであり、そのため上記のような奇妙な現象が見られるのであるということができる。独立変数 t と関数値 y との関係を表す2次元平面の原点(0, 0)においてこの面に直交する第三の座標軸は関数 y(t)の定数項の値を表す。この座標軸を定数項軸と呼ぶことにする。(5.69)の区間(0≤t<1)の関数は定数項軸の C 点においてこの軸に直交する2次元平面にある関数である。区間(1≤t)の関数は定数項軸の y(0)=C+3/4 の点においてこの軸に直交する2次元平面にある関数の(1≤t)の部分である。従って、(5.69)の関数はこの3次元空間においては接続していない。微分演算が定数項に無関係なのは、関数 y(t)の t 軸方向の編微分を求める演算であり、定数項軸方向の微分には無関係だからである。被微分関数は定数項を減算するのも同じ意味であり、微分結果はその定数項の位置にある2次元平面に移動する。逆に、積分演算はその結果の関数が存在する2次元平面の位置を定めなければならないから積分定数を必要とする。従来の議論はこの3次元空間の全ての2次元平面を定数項軸の原点にある2次元平面に重ねて眺めているから(5.68)(A)や(5.69)の関数は接続しているように見えるのである。
. .
ユニットステップ関数 u(t)やその導関数であるインパルス関数 δ(t)を用いると、(5.68)や(5.69)の関数を一つの2次元平面にある連続関数として扱うことができる。(5.68)や(5.69)の関数のそれぞれの部分を構成する関数を連続関数 f(t)及び g(t)で表すと、全体を表す関数 y(t)は(5.70)で表すことができる。f(1)≠g(1)であっても両関数はユニットステップ関数で接続されている。ユニットステップ関数は u(0)=0, u(+0)=1 であるが、無限に連続微分可能関数であるから(5.70)の y(t)は連続関数である。従って、連続関数の定義は変更しなければならない。
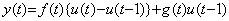 ______(5.70). .
関数 y(t)の導関数 y'(t)は(5.71)で表される。f(1)=g(1)且つ f(0)=0であれば、この導関数は f(t)の導関数と g(t)の導関数を t=1 においてユニットステップ関数で接続した関数であり、f(1)≠g(1)なら、更にインパルス関数を重畳した関数である。f(0)≠0 なら、t=0 にもインパルス関数が存在する。この関数は更に無限に連続微分可能である。従って、連続関数とは無限に連続微分可能関数を言うと定義できる。 ______(5.70). .
関数 y(t)の導関数 y'(t)は(5.71)で表される。f(1)=g(1)且つ f(0)=0であれば、この導関数は f(t)の導関数と g(t)の導関数を t=1 においてユニットステップ関数で接続した関数であり、f(1)≠g(1)なら、更にインパルス関数を重畳した関数である。f(0)≠0 なら、t=0 にもインパルス関数が存在する。この関数は更に無限に連続微分可能である。従って、連続関数とは無限に連続微分可能関数を言うと定義できる。
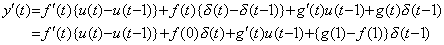 ______(5.71). .
(5.54)の関数 y(t)はユニットステップ関数を掛けることにより y(0)=0 の連続関数とすることは出来ない。(5.72)の第1式だけ見れば問題ないように見える。しかし、導関数 y'(t)は第2式で表され、数値零の平方根は零であるから第2項のインパルス関数は消えるが、第1項は無限大掛ける零となり、導関数 y'(t)は t=0 で不連続である。従って、関数 y(t)も t=0 で不連続である。(5.70)の構成関数がその区間において不連続関数の場合はユニットステップ関数を用いても連続関数に変換することは出来ない。 ______(5.71). .
(5.54)の関数 y(t)はユニットステップ関数を掛けることにより y(0)=0 の連続関数とすることは出来ない。(5.72)の第1式だけ見れば問題ないように見える。しかし、導関数 y'(t)は第2式で表され、数値零の平方根は零であるから第2項のインパルス関数は消えるが、第1項は無限大掛ける零となり、導関数 y'(t)は t=0 で不連続である。従って、関数 y(t)も t=0 で不連続である。(5.70)の構成関数がその区間において不連続関数の場合はユニットステップ関数を用いても連続関数に変換することは出来ない。
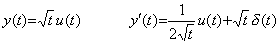 ______(5.72) ______(5.72)
5.5 本演算子法の演算子のノルム
. .
二つのベクトルの積 YZ は乗数ベクトル Y を行列 Y に展開する、即ち、YZ=YZ によって実行される。この行列 Y は演算子であり、演算子値を表すから、そのノルムはベクトル Y のノルムに同じでなければならない。従って、ベクトルが行列展開された演算子のノルムは関数の絶対値の最大値であり、又、等間隔区分点の間隔が適当な値であるなら、行列 Y の対角要素のなかで絶対値最大の要素の値に等しい。そのノルムはベクトルのノルム||Y||を行列展開した行列で表される。
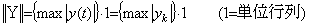 ______(5.73)
(5.73)において単位行列は省略してもよい。何故なら、対角要素が全て同じであるとき、本演算子法はその対角行列を数で表してよいからである。 ______(5.73)
(5.73)において単位行列は省略してもよい。何故なら、対角要素が全て同じであるとき、本演算子法はその対角行列を数で表してよいからである。
. .
積分演算子や微分演算子はベクトルの形で表すことはできない。これら演算子の対角要素及びそれより下にある要素は定数ベクトルを行列展開した演算子に同じであるけれど、対角要素より上にある要素は全てが零ではない。しかし、その行列、即ち、演算子値は被演算子によっても変数 t によっても変化しない。第2章1.2節において著者は、積分演算子は反復演算によりその次元数を増加すると述べた。それは被演算ベクトルの高次行要素が全て零であるのでその記述を省略していることによるものである。又、その演算子値は変数 t が初期値点 t0 から正の方向に変化するなら被演算子の符号も変えない。従って、この演算子値は正の一定値であり、この演算子のノルムはその演算子値に同じでなければならない。
. .
差分演算子 Δ は第2.3節の(2.5)の行列で表される。その対角要素及びそれより下の要素は全て零であるが、対角要素より一つ右の要素が 1 でその他は零である。この行列は被演算子及び変数 t によって変わらないから、その演算子値は一定値である。従って、差分演算子 Δ のノルムはその演算子値に同じでなければならず、Δ で表されなければならない、即ち、||Δ||=Δ である。差分演算子のノルム||Δ||とベクトルのノルム||Y||の積はノルム||Y||をベクトルで表すと零になる。しかし、差分演算子のノルム||Δ||とベクトル Y を行列展開した演算子のノルムとの積は零ではない。ベクトル Y とベクトル Z とのノルムの積はベクトルの形の積でも、演算子としてのノルム、即ち、行列展開した積でも同じであるが、一方が差分演算子のようにベクトルの形をもたない場合には他方も行列の形のノルムで演算しなければならない。
. .
関数 y(t) が定数項 y0 を持つとき、その差分演算は(5.74)に示すように二通りに定義される。微分演算と同様に、第1式は差分方程式に変換する演算で初期値 y0 との対が演算結果となる。第2式が導関数に相当する差分関数を求める通常の差分演算であり、この差分演算子の被演算関数は y(t)−y0 である。この演算はその導関数 f(t) を用いて(5.75)で表すことができる。
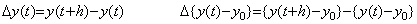 ______(5.74) ______(5.74)
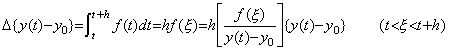 ______(5.75)
差分演算の定義は被演算関数により変化しないから、形式的に演算子 Δ を掛けることでこの演算を表記するとき、その演算子値は一定値でなければならない。しかし、一定値を掛けて差分演算が出来るのは、微分演算と同様に被演算関数が一次関数の場合だけである。一般的にそれが可能であるためには、(5.75)の[ ]で示す被演算関数とその導関数の平均関数との対を全て要素とする集合を演算子として導入しなければならない。その集合は一つしかないから演算子値は一定値であり、差分演算子値はその集合の要素の値と h の積で決まるから集合としての演算子値は 1 でなければならない。或いは、h が[ ]で表した演算子の集合としての値である。従って、差分演算子値及びノルムは||Δ||=Δ=h である。(5.45)及び(5.46)に示した微積分演算の場合も、関数とその平均関数との対を要素とする演算子の集合としての値が積分演算の場合は t、微分演算の場合は 1/t であるとも言える。 ______(5.75)
差分演算の定義は被演算関数により変化しないから、形式的に演算子 Δ を掛けることでこの演算を表記するとき、その演算子値は一定値でなければならない。しかし、一定値を掛けて差分演算が出来るのは、微分演算と同様に被演算関数が一次関数の場合だけである。一般的にそれが可能であるためには、(5.75)の[ ]で示す被演算関数とその導関数の平均関数との対を全て要素とする集合を演算子として導入しなければならない。その集合は一つしかないから演算子値は一定値であり、差分演算子値はその集合の要素の値と h の積で決まるから集合としての演算子値は 1 でなければならない。或いは、h が[ ]で表した演算子の集合としての値である。従って、差分演算子値及びノルムは||Δ||=Δ=h である。(5.45)及び(5.46)に示した微積分演算の場合も、関数とその平均関数との対を要素とする演算子の集合としての値が積分演算の場合は t、微分演算の場合は 1/t であるとも言える。
. .
微積分演算子の場合は、[ ]で表した演算子の要素は被演算関数とその平均関数の対であり、被演算子の特性だけで決まる要素である。しかし、上記の差分演算子の要素は被演算関数とその導関数の平均関数との対であり、この差分演算子は微分演算子の要素を含む複合演算子である。微分演算子の要素を含まない差分演算子は(5.76)に示すようにシフト演算子 E と恒等演算子を用いて表される。シフト演算の定義は被演算関数が何であってもそれを t 軸方向に移動するだけであるから、演算子値は一定値であり、||E||=E=1 である。従って、差分演算子値は零になってしまうが、これは演算子値やそのノルムに位相の概念がないことによるものであり、実際は零ではない。その値は明確にできないが、差分演算子は||Δ||=Δ>0、シフト演算子は||E||=E>1 である。
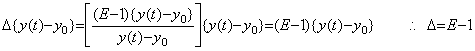 ______(5.76). .
(5.74)の差分演算は、h→0 の極限では差分結果は恒等的に零の関数となる。しかし、差分法の差分演算では差分結果は区分幅 h には無関係である。これは、差分法では区分幅に応じて時間変数を変換するからである。時間変数 t=t0+nh は t0 を 0 に変換して関数値を y0 で表し、t を n に変換してその関数値を yn で表す。従って、常に h=1 に変換されるから差分演算子値が 0 になることはなく、シフト演算子値が 1 になることもない。従って、逆演算子 Δ−1、E−1 が存在する。 ______(5.76). .
(5.74)の差分演算は、h→0 の極限では差分結果は恒等的に零の関数となる。しかし、差分法の差分演算では差分結果は区分幅 h には無関係である。これは、差分法では区分幅に応じて時間変数を変換するからである。時間変数 t=t0+nh は t0 を 0 に変換して関数値を y0 で表し、t を n に変換してその関数値を yn で表す。従って、常に h=1 に変換されるから差分演算子値が 0 になることはなく、シフト演算子値が 1 になることもない。従って、逆演算子 Δ−1、E−1 が存在する。
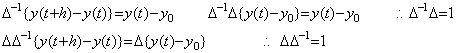 ______(5.77) ______(5.77)
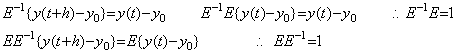 ______(5.78). .
本演算子法のベクトルは、微積分演算や差分演算の数式で集合として[ ]で示した演算子のように、逐次階差を要素とする順序集合であり、その集合としての値がベクトルの大きさ及びノルムであり、それは関数のノルムである。ベクトルの差分演算を行う差分演算子は上記の差分演算子とは少し異なる。(5.79)に示すように、被演算ベクトルが何であっても、即ち、その表す関数が何であっても、差分演算は被演算ベクトルの各要素に差分演算子 Δ を掛けることで実行できる。従って、差分演算子値は Δ であり、そのノルムも||Δ||=Δである。ベクトルの要素ではなくベクトルに差分演算子 Δ を掛けるには、差分演算子を対角要素の一つ右の要素が 1 でその他の要素は全て零である行列で表さねばならない。差分演算子 Δ とこの行列は等価であり、Δ>0 である。二つのベクトルの積は左のベクトルを行列展開して実行するのと同様に、差分演算子 Δ とベクトルの積も差分演算子を行列展開して実行されるのである。この行列を差分演算子 Δ の行列展開と呼ぶ。 ______(5.78). .
本演算子法のベクトルは、微積分演算や差分演算の数式で集合として[ ]で示した演算子のように、逐次階差を要素とする順序集合であり、その集合としての値がベクトルの大きさ及びノルムであり、それは関数のノルムである。ベクトルの差分演算を行う差分演算子は上記の差分演算子とは少し異なる。(5.79)に示すように、被演算ベクトルが何であっても、即ち、その表す関数が何であっても、差分演算は被演算ベクトルの各要素に差分演算子 Δ を掛けることで実行できる。従って、差分演算子値は Δ であり、そのノルムも||Δ||=Δである。ベクトルの要素ではなくベクトルに差分演算子 Δ を掛けるには、差分演算子を対角要素の一つ右の要素が 1 でその他の要素は全て零である行列で表さねばならない。差分演算子 Δ とこの行列は等価であり、Δ>0 である。二つのベクトルの積は左のベクトルを行列展開して実行するのと同様に、差分演算子 Δ とベクトルの積も差分演算子を行列展開して実行されるのである。この行列を差分演算子 Δ の行列展開と呼ぶ。
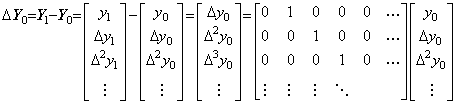 ______(5.79). .
差分演算子 Δ の行列展開は逆行列が存在しないが、差分演算子 Δ の逆演算子は存在する。厳密に言えば、(5.79)の差分演算子 Δ の被演算ベクトルは初期値 y0 を減算したものでなければならない。従って、(5.80)のように記述するべきである。しかし、差分演算子 Δ の行列展開の第一列が全て零であることが初期値を減算して除去することを意味しているので(5.79)で記述しても差支えない。但し、逆演算は初期値を減算した(5.80)の逆演算でなければならないので(5.81)で表される。逆演算子のノルムは||Δ−1||=Δ−1 である。 ______(5.79). .
差分演算子 Δ の行列展開は逆行列が存在しないが、差分演算子 Δ の逆演算子は存在する。厳密に言えば、(5.79)の差分演算子 Δ の被演算ベクトルは初期値 y0 を減算したものでなければならない。従って、(5.80)のように記述するべきである。しかし、差分演算子 Δ の行列展開の第一列が全て零であることが初期値を減算して除去することを意味しているので(5.79)で記述しても差支えない。但し、逆演算は初期値を減算した(5.80)の逆演算でなければならないので(5.81)で表される。逆演算子のノルムは||Δ−1||=Δ−1 である。
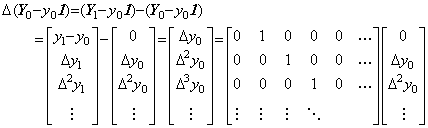 ______(5.80) ______(5.80)
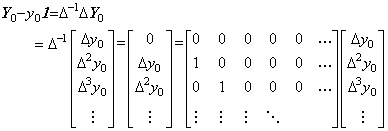 ______(5.81). .
行列演算では Δ−1 の行列展開の第一行が全て零であるので、被演算ベクトル ΔY0 の要素を1行下に下げ、第1要素に零をセットする。被演算ベクトル ΔY0 の各要素に Δ−1 を掛ける演算では Δ−1Δ=1 を用いて演算すればよい、但し、y0=0 である。差分演算子 Δ とその逆演算子 Δ−1 の積は、ΔΔ−1=1 であるが Δ−1Δ≠1 であると従来言われている。これは、差分演算子は初期値を零に変換するという間違った議論によるものである。正しくは、差分演算子の被演算関数は初期値を減算したもの、従って、初期値は零でなければならない。差分演算子と逆演算子を行列展開して掛けると、ΔΔ−1=1、即ち、単位行列になるが、(5.82)に示すように、Δ−1Δの1行1列は零であり、単位行列ではない。しかし、被演算ベクトルの第1要素が y0=0 であるから、単位行列の1行1列は 1 でも 0 でも同じであり、Δ−1Δ=1 である。 ______(5.81). .
行列演算では Δ−1 の行列展開の第一行が全て零であるので、被演算ベクトル ΔY0 の要素を1行下に下げ、第1要素に零をセットする。被演算ベクトル ΔY0 の各要素に Δ−1 を掛ける演算では Δ−1Δ=1 を用いて演算すればよい、但し、y0=0 である。差分演算子 Δ とその逆演算子 Δ−1 の積は、ΔΔ−1=1 であるが Δ−1Δ≠1 であると従来言われている。これは、差分演算子は初期値を零に変換するという間違った議論によるものである。正しくは、差分演算子の被演算関数は初期値を減算したもの、従って、初期値は零でなければならない。差分演算子と逆演算子を行列展開して掛けると、ΔΔ−1=1、即ち、単位行列になるが、(5.82)に示すように、Δ−1Δの1行1列は零であり、単位行列ではない。しかし、被演算ベクトルの第1要素が y0=0 であるから、単位行列の1行1列は 1 でも 0 でも同じであり、Δ−1Δ=1 である。
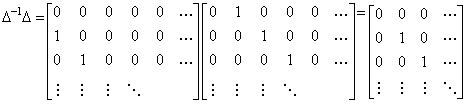 ______(5.82). .
シフト演算子 E は次のように表され、||E||=E である。シフト演算子 E の行列展開は差分演算子 Δ の行列展開の対角要素を全て 1 に換えた行列である。この行列は逆行列が存在し、それが逆演算子 E−1 の行列展開である。逆演算子のノルムは||E−1||=E−1 である。 ______(5.82). .
シフト演算子 E は次のように表され、||E||=E である。シフト演算子 E の行列展開は差分演算子 Δ の行列展開の対角要素を全て 1 に換えた行列である。この行列は逆行列が存在し、それが逆演算子 E−1 の行列展開である。逆演算子のノルムは||E−1||=E−1 である。
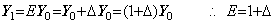 ______(5.83). .
微分演算は第3.5節の(3.37)で表され、被演算ベクトルはY0−y01 であり、初期値、即ち、第1要素が零のベクトルであるが、差分演算子 Δ はこの第1要素を取除くだけなので(5.84)に示すように被演算ベクトルは ΔY0 で表すことができる。h−1ΔY0 は関数 y(t)の微分の平均値を表す関数 f(ξ t)に相当する。従って、行列 D は(5.46)の平均関数 f(ξ t)を関数 f(t)に変換する演算子に相当するが、行列 D の演算子値は 1 ではない。等間隔区分点の関数 y(t)の微分の平均値 f(ξ)=h−1{y(t+h)−y(t)}を与える点 t<ξ<t+h は等間隔区分点上にない。従って、平均関数f(ξ t)に相当するベクトルを関数 f(t)、即ち、導関数 y'(t)のベクトルに変換するには位相の補正が必要であり、それが行列 D の演算子値が 1 でない理由である。しかし、この行列は一つしかないのであり、演算子値は一定値である。ΔY0 の第4階差以上の階差が全て零の場合は、行列 D は3行3列で表せるが、その他の要素を表記することは意味がないから省略されたのであり、異なる行列 D が存在するのではない。本演算子法における微分演算子値及びそのノルムは||h−1D||=h−1D と表され、微分演算子の行列展開である。 ______(5.83). .
微分演算は第3.5節の(3.37)で表され、被演算ベクトルはY0−y01 であり、初期値、即ち、第1要素が零のベクトルであるが、差分演算子 Δ はこの第1要素を取除くだけなので(5.84)に示すように被演算ベクトルは ΔY0 で表すことができる。h−1ΔY0 は関数 y(t)の微分の平均値を表す関数 f(ξ t)に相当する。従って、行列 D は(5.46)の平均関数 f(ξ t)を関数 f(t)に変換する演算子に相当するが、行列 D の演算子値は 1 ではない。等間隔区分点の関数 y(t)の微分の平均値 f(ξ)=h−1{y(t+h)−y(t)}を与える点 t<ξ<t+h は等間隔区分点上にない。従って、平均関数f(ξ t)に相当するベクトルを関数 f(t)、即ち、導関数 y'(t)のベクトルに変換するには位相の補正が必要であり、それが行列 D の演算子値が 1 でない理由である。しかし、この行列は一つしかないのであり、演算子値は一定値である。ΔY0 の第4階差以上の階差が全て零の場合は、行列 D は3行3列で表せるが、その他の要素を表記することは意味がないから省略されたのであり、異なる行列 D が存在するのではない。本演算子法における微分演算子値及びそのノルムは||h−1D||=h−1D と表され、微分演算子の行列展開である。
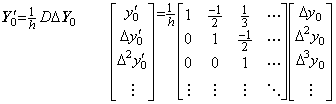 ______(5.84). .
積分演算は第4.4節の (4.28)で表され、演算結果はベクトルY0−y01 であり、この第1要素は零であるが、差分演算子 Δ によりこれを取除いてベクトル ΔY0 で表せる。(5.85)の行列と被演算ベクトルの積は積分の平均関数を表すが、(5.45)の被積分関数を積分の平均関数に変換する演算子とは異なり、行列 D−1 の演算子値は 1 ではない。被積分関数 f(t)=y'(t)の積分の平均値 f(ξ t)を与える点ξ t は被積分ベクトルの要素を与える区分点上にないので位相の補正が必要だからである。行列 D−1 は一つしかないので、本演算子法における積分演算子値及びそのノルムは一定値であり、||hD−1||=hD−1 と表され、積分演算子の行列展開である。 ______(5.84). .
積分演算は第4.4節の (4.28)で表され、演算結果はベクトルY0−y01 であり、この第1要素は零であるが、差分演算子 Δ によりこれを取除いてベクトル ΔY0 で表せる。(5.85)の行列と被演算ベクトルの積は積分の平均関数を表すが、(5.45)の被積分関数を積分の平均関数に変換する演算子とは異なり、行列 D−1 の演算子値は 1 ではない。被積分関数 f(t)=y'(t)の積分の平均値 f(ξ t)を与える点ξ t は被積分ベクトルの要素を与える区分点上にないので位相の補正が必要だからである。行列 D−1 は一つしかないので、本演算子法における積分演算子値及びそのノルムは一定値であり、||hD−1||=hD−1 と表され、積分演算子の行列展開である。
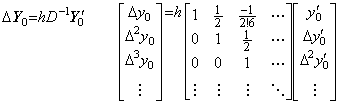 ______(5.85)
目 次 へ ______(5.85)
目 次 へ
|
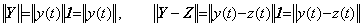 _____(5.1)
_____(5.1) . .
空間 Rp+1 で起こる現象を空間 Rp の現象として観測すると、空間 Rp には実際には存在しない現象があたかも存在するように見える。3次元ユークリッド空間において Fig. 5.1 に示すような振子を考える。重力は x−y 面に垂直とし、振子はその錘が原点の周りを回るように振られているとする。振子の錘を月と呼び、原点にある球体を地球と呼ぶことにする。我々が x−y 平面で表される2次元空間に居るなら、月が地球の周りを回転するのは見えるが振子の紐および重力は見えず、月が地球の周りを回転するのを止めれば月は地球に落ちるのを見る。月と地球は紐で繋がれていないにもかかわらず両者の間には力が働き、それは万有引力が存在するかのように見える。或いは、紐の正射影が両者を繋いでいるのが見えるのかもしれないが、その紐は目には見えるが触ることのできない不思議な紐である。実際には、我々は3次元空間に居てその求心力は振子の紐の張力の x−y 平面への正射影であることが分かる。ここで、2次元空間に居る我々が求めたいものは月 M に働く真の力、即ち、3次元空間の紐に働く張力である。しかし、張力の z 軸成分は x−y 平面に直交しているため見ることができない。x−y 平面の成分からそれを推測することも不可能である。月 M に働く真の力を知るためには3次元空間に出なければならない。
. .
空間 Rp+1 で起こる現象を空間 Rp の現象として観測すると、空間 Rp には実際には存在しない現象があたかも存在するように見える。3次元ユークリッド空間において Fig. 5.1 に示すような振子を考える。重力は x−y 面に垂直とし、振子はその錘が原点の周りを回るように振られているとする。振子の錘を月と呼び、原点にある球体を地球と呼ぶことにする。我々が x−y 平面で表される2次元空間に居るなら、月が地球の周りを回転するのは見えるが振子の紐および重力は見えず、月が地球の周りを回転するのを止めれば月は地球に落ちるのを見る。月と地球は紐で繋がれていないにもかかわらず両者の間には力が働き、それは万有引力が存在するかのように見える。或いは、紐の正射影が両者を繋いでいるのが見えるのかもしれないが、その紐は目には見えるが触ることのできない不思議な紐である。実際には、我々は3次元空間に居てその求心力は振子の紐の張力の x−y 平面への正射影であることが分かる。ここで、2次元空間に居る我々が求めたいものは月 M に働く真の力、即ち、3次元空間の紐に働く張力である。しかし、張力の z 軸成分は x−y 平面に直交しているため見ることができない。x−y 平面の成分からそれを推測することも不可能である。月 M に働く真の力を知るためには3次元空間に出なければならない。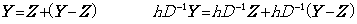 _____(5.1a)
_____(5.1a)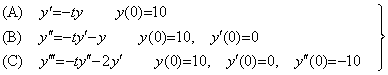
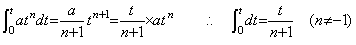 _____(5.2)
_____(5.2)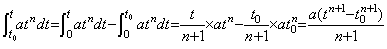 ____(5.3)
____(5.3)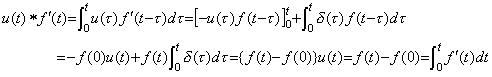 __(5.4)
__(5.4)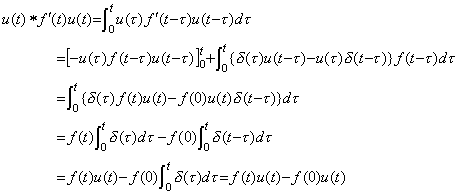 __(5.5)
__(5.5)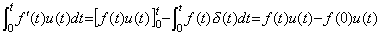 _____(5.6)
_____(5.6)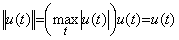 ________(5.7)
________(5.7)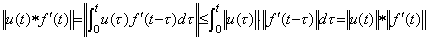 ____(5.8)
____(5.8)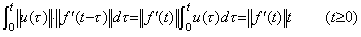 _____(5.9)
_____(5.9)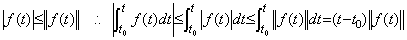 ____(5.10)
____(5.10)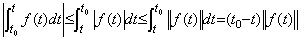 _____(5.11)
_____(5.11)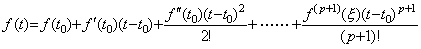 ____(5.12)
____(5.12)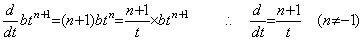 _____(5.13)
_____(5.13)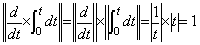 ______(5.14)
______(5.14)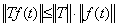 ______(5.15)
______(5.15)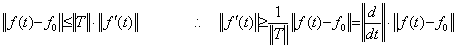 _____(5.16)
_____(5.16)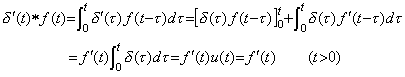 ____(5.17)
____(5.17)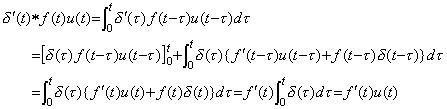 ___(5.18)
___(5.18)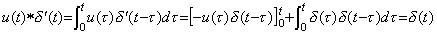 ___(5.19)
___(5.19)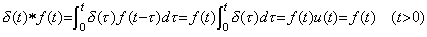 ____(5.20)
____(5.20)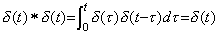 ______(5.21)
______(5.21)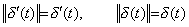 ________(5.22)
________(5.22)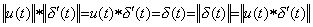 ____(5.23)
____(5.23)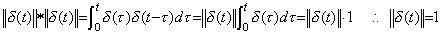 ___(5.24)
___(5.24)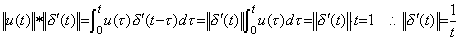 ___(5.25)
___(5.25)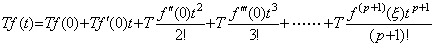 ___(5.26)
___(5.26)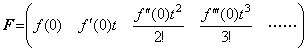 ____(5.27)
____(5.27)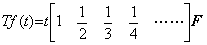 ____(5.28)
____(5.28)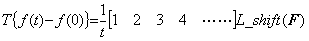 _____(5.29)
_____(5.29)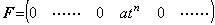 _____(5.30)
_____(5.30)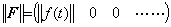 ____(5.31)
____(5.31)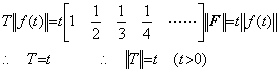 ____(5.32)
____(5.32)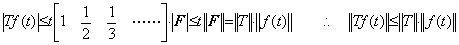 ___(5.33)
___(5.33)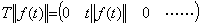 ____(5.34)
____(5.34)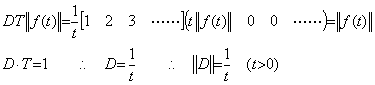 _____(5.35)
_____(5.35)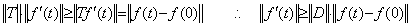 _____(5.36)
_____(5.36)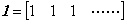 ________(5.37)
________(5.37)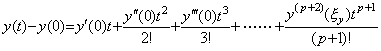 ____(5.38)
____(5.38) _____(5.39)
_____(5.39) _____(5.40)
_____(5.40)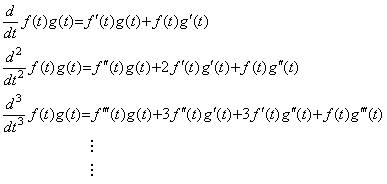 ____(5.41)
____(5.41)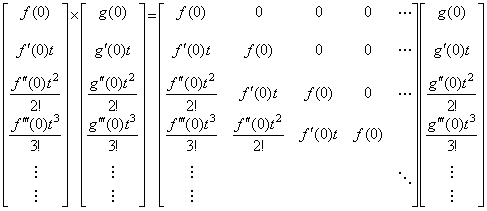 ___(5.42)
___(5.42)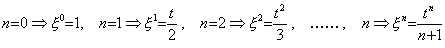 _______(5.43)
_______(5.43)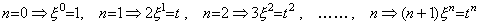 _________(5.44)
_________(5.44)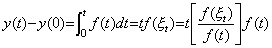 _________(5.45)
_________(5.45)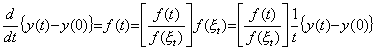 ________(5.46)
________(5.46)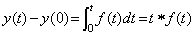 _______(5.47)
_______(5.47)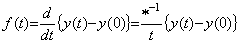 ____(5.48)
____(5.48)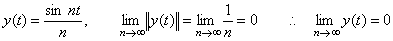 ____(5.49)
____(5.49)
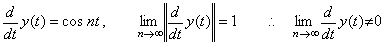 _____(5.50)
_____(5.50)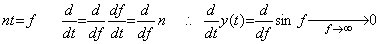 _____(5.51)
_____(5.51)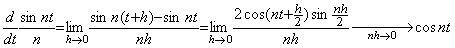 _____(5.52)
_____(5.52)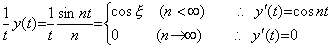 ____(5.53)
____(5.53)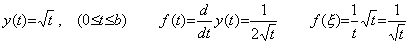 ____(5.54)
____(5.54)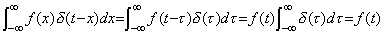 _____(5.55)
_____(5.55)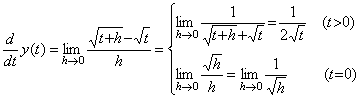 _____(5.56)
_____(5.56)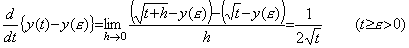 _____(5.57)
_____(5.57)
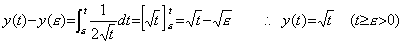 ________(5.58)
________(5.58)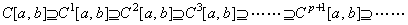 _____(5.59)
_____(5.59)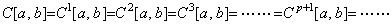 ______(5.60)
______(5.60)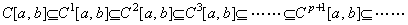 ______(5.61)______[Q.E.D.]
______(5.61)______[Q.E.D.]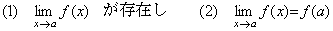 ______(5.62)
______(5.62)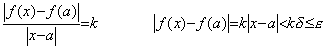 ______(5.63)
______(5.63) ______(5.64)
______(5.64)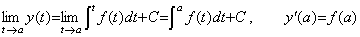 ______(5.65)______[Q.E.D.]
______(5.65)______[Q.E.D.]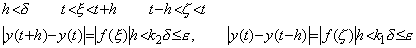 ______(5.66)
______(5.66)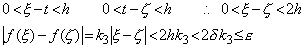 ______(5.67)
______(5.67)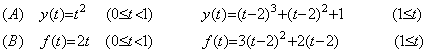 ______(5.68)
______(5.68)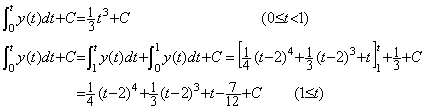 ______(5.69)
______(5.69)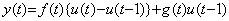 ______(5.70)
______(5.70)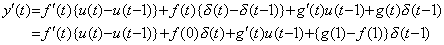 ______(5.71)
______(5.71)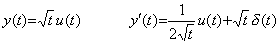 ______(5.72)
______(5.72)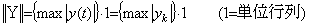 ______(5.73)
______(5.73)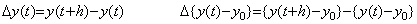 ______(5.74)
______(5.74)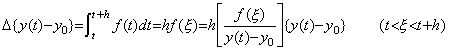 ______(5.75)
______(5.75)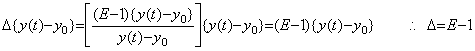 ______(5.76)
______(5.76)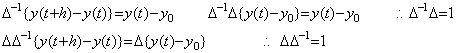 ______(5.77)
______(5.77)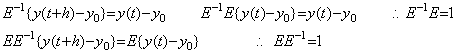 ______(5.78)
______(5.78)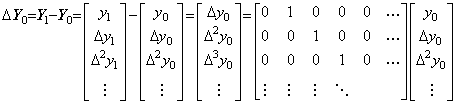 ______(5.79)
______(5.79)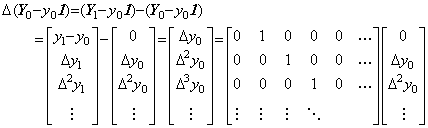 ______(5.80)
______(5.80)
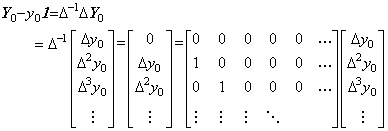 ______(5.81)
______(5.81) ______(5.82)
______(5.82) ______(5.83)
______(5.83)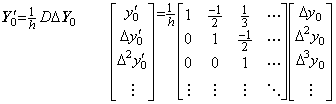 ______(5.84)
______(5.84)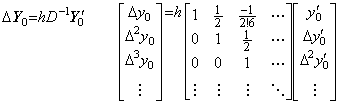 ______(5.85)
______(5.85)