4.5. .予測子と修正子
. .
微分演算子は微分方程式の解を得、その演算は(4.35)で表される。その演算は初期値を除いて(4.31)を用いて実行されねばならない。被積分ベクトル Y0' が y0' から yp−1' 迄の p 個の値で構成されているなら、(4.28)に示すように、解 ΔY0 は y0 から yp 迄の p+1 個の値により構成される。従って、最後の点 tp における yp' の値は結果に影響を与えない。その結果、被積分関数が p−1 次関数なら結果は剰余項のない p 次関数になる。しかし、被積分関数が任意の連続関数なら、yp' の影響のある解の方が被積分関数が高次関数であるから yp' を使用しない解よりよい精度を持つであろう。
. .
著者は Δ を掛けた積分演算子、即ち、(4.28)の hD−1 を予測子と名付ける。その理由は、被積分関数の t0 から tp−1 迄を用いて t0 から tp 迄の積分を求めるからである。従来の予測子は yp を y0', y1', ………, yp−1' で表せば逐次の p の値に対して以下に示すように得られる。
. .
行列 D−1 が1次、即ち、p=1 のときは、行列演算式は
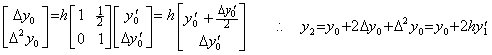
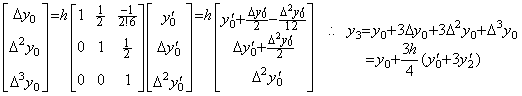
. . 行列 D−1 が(1×2)次のとき Euler 法の修正子であり、次に示すように台形法である。
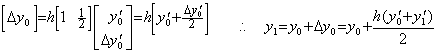
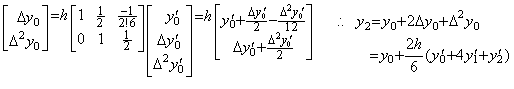
. . 行列 D−1 が(3×4)次のとき Simpson の 3/8 則である。即ち、
. . 微分方程式 y' =−ty の Milne 法による解を反復修正毎にプリントアウトすると、それらは t=0 の近傍では1回ないし2回の反復修正で正確な解に漸近するが、t=5 の近傍では修正子を何回も反復しても正確な解に漸近しないことが分かる。その原因は t=0 の近傍では Simpson の 1/3 を修正子として使用することは十分であるが、 t=5 の近傍では十分でないことである。第2章1節及び2節で述べたように、中点法を用いることで十分であるから Milne の予測子を用いることは効果がない。
. . (4.31)において、演算子は p 次の正方行列であるからベクトル ΔY0 及び Y0' は同数個の要素を持つ。修正子は t0 から tp 迄の積分を被積分関数の t0 から tp 迄を用いて求めなければならないから、最後の要素 Δpy0' をベクトル Y0' に追加しなければならない。その場合、演算子は p+1 次の行列になり、ベクトル ΔY0 は最後の要素 Δp+1y0 を持つ。それは ΔY0 に ΔT を左より掛けることにより取り除かれ、ベクトル ΔTΔY0 は初期値零を第1要素として持つ。(4.33)に示したように、この演算は y' (t) の t から t+h 迄の積分を y' (t) の t0 から t+h 迄の積分から減算することを意味し、その行列演算式は(4.34)で表される。初期値 y0 を(4.33)の両辺に加えると解 y(t) が得られる。それは(4.35)で表され、また、次の式でも表される。
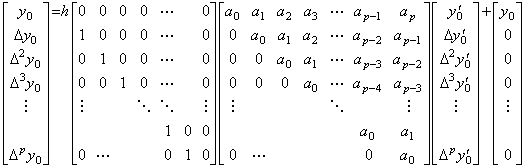
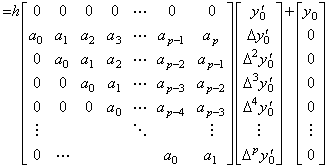
 ____(4.40)
____(4.40). . (4.35)の積分演算子 h(ΔD)−1 は、(4.39)を詳細に表した演算式に示したように、t0 から tp 迄の積分を被積分関数の t0 から tp 迄を用いて求めるから厳密に言えば修正子である。しかし、最後の要素 Δpy0' が未知のときそれを零であると仮定すれば、その演算子は t0 から tp 迄の積分を被積分関数の t0 から tp−1 迄を用いて求め、この仮定は予測を意味する。故に、著者は通常予測子と修正子の区別なしに(4.31)及び(4.35)の両方を使用する。
. . 与えられた関数の積分を得たいとき、通常は p 次の予測子より精度のよい結果を与える(p×(p+1))次の修正子を用いるのがよい。与えられた微分方程式の解を得たいときは、以下に示すように予測子と修正子の対を用いることができる。
. . 本解法においては必要とされる出発値は初期値一つだけであり、先ず最初に与えられた初期値 y0 により y0' を求める。それから逐次に、1次の予測子、(1×2)次の修正子、2次の予測子、(2×3)次の修正子、………、p 次の予測子、(p×(p+1))次の修正子と用いて必要な精度の p 個の解を求める。最後の修正子以外の修正子は全て省略することができる。何故なら、k 次の予測子は((k−1)×k)次の修正子を含んでいるからである。
. . 最後の修正子は次数 p を固定したまま何回も反復繰り返し使用してはならない。その理由は、2ないし3回の繰り返しを除き、より良い精度の結果を得るうえで効果がなく、従来の予測子・修正子法のように不安定現象となる原因であるからである。
4.6 2重積分演算子
. .
導関数 y' (t) は y(t)−y0 の微分によって得られ、2次導関数 y"(t) は y' (t)−y0' の微分によって得られる。故に、
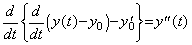 ____(4.42)
____(4.42)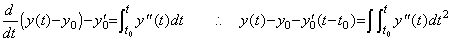 ___(4.43)
___(4.43)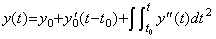 _____(4.44)
_____(4.44). .
[定理 4.9]. .(4.43)から y0 及び y0' を消去すると、
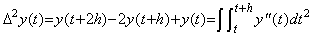 _____(4.45)
_____(4.45)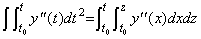
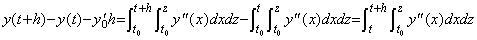
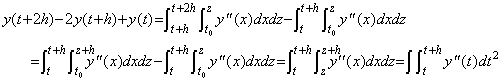
| [Q.E.D.] |
[補足]
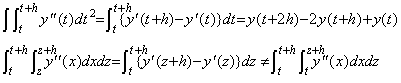
. . [定理 4.10]. .m≥0 のとき、Δmy"(t) の t から t+h 迄の2重積分は、
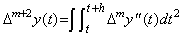 _____(4.46)
_____(4.46)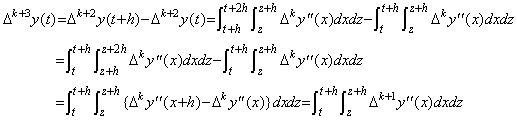
| [Q.E.D.] |
補足
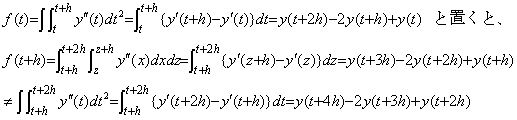
. . [定理 4.11]. . y(t)∈Cp+1[a, b] 及び 1≤m≤p+1 と仮定すると次のような ξ が存在する。
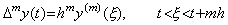 ______(4.47)
______(4.47)| 1). . | m=1 のとき、. .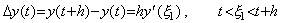 |
| 2) | m=2 のとき、. .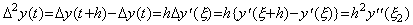 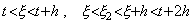 |
| 3) | m=n のとき成立すると仮定すると m=n+1 のときは、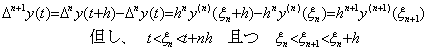 . .[Q.E.D.] . .[Q.E.D.] |
. . [定理 4.12]. . y(t)∈Cp+1[a, b] と仮定すると、Δmy(t) は t=t0+rh∈[a, b] を満たす実数 r に対して(4.48)で表される。
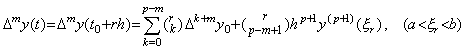 ___(4.48)
___(4.48)| 1) | . .m=0 のとき、(4.48)は定理 3.1 に示した y(t) の Newton の補間公式である。 |
| 2) | . . m=1 のとき、定理 3.3 に示したようにその補間公式の階差である。Δy(t)∈Cp+1[a, b] であるが、剰余項が零になる等間隔区分点の数は r=0 から p−1 迄の p 点に減少する。 |
| 3) | . .m=n のとき成立すると仮定すれば、定理 4.11 により次のような値 ξ が存在する。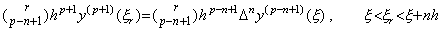 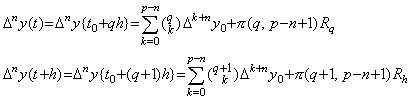 . . 関数 Δny(t0+uh) と定数 Rq を持つ近似関数との残差として関数 F(u) を考えると、関数 G(u) 即ち F(u+1) は関数 Δny{t0+(u+1)h} と Rh の代わりに定数 Rq を持つ近似公式との残差である。G(u)−F(u) は u=0 から p−n−1 及び r の p−n+1 点で零になることを用いると定理 3.3 の証明と同様にして次の結果が得られる。 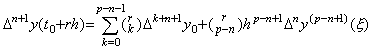 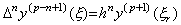 を満たす ξ r が存在する。. .[Q.E.D.] を満たす ξ r が存在する。. .[Q.E.D.]
|
. . 上記証明の 3) は直接(4.48)の m に n を代入した式を用いて以下のように示してもよい。
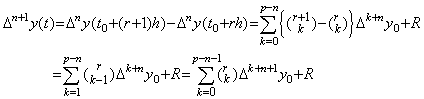
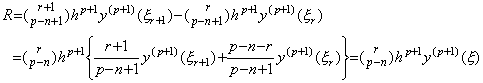
. . 2次微分演算の逆演算は(4.43)で表される。それを行列演算式で表すとき左辺の逐次階差を求めなければならない。t=t0 なら左辺は y(t)−y0−y0' (t−t0)=0 になるが、これは2重積分の結果ではない。t=t0+h なら左辺は2重積分の結果であるが、左辺の2つの値の差は Δy0−
. .[定理 4.13]. .
y"(t)∈Cp−1[a, b] のとき、それを Newton の補間公式で表すと、2重積分の結果の逐次階差は、
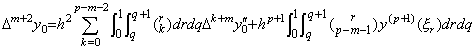 ___(4.49)
___(4.49)[証明]. .y(t) と y"(t) の関係は(4.46)で表される。それに t=t0 を代入すると、Δm+2y0 が得られる。
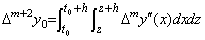
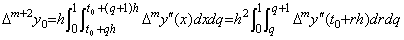 ____(4.50)
____(4.50)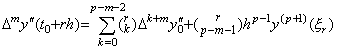
| [Q.E.D.] |
. . [定理 4.14]. .(4.49)の Δk+my0" の係数にある2重積分を ak2で表すと、
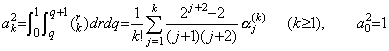 ____(4.51)
____(4.51)[証明]. .Stirling 数を用いると、
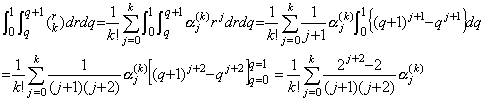
| [Q.E.D.] |
. . Table 3.3 の Stirling 数を用いると、(4.51)の値は k=0 から 10 迄に対して次のように求められる。
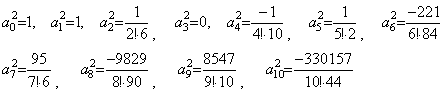
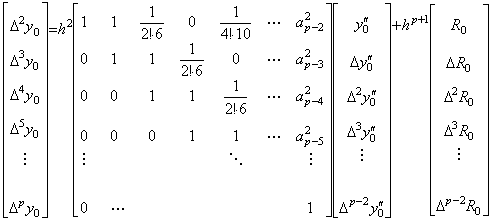 __(4.52)
__(4.52)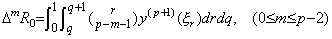
. . m の値が m=p−1 のとき、(4.49)は剰余項のみとなる。
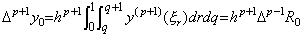 _____(4.53)
_____(4.53)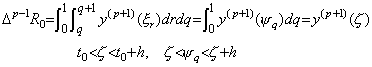
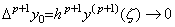
従って、それは行列演算式(4.52)に表されない。
. .[定理 4.15]. .h→0 なら(4.52)の剰余項は hp+1R→0 である。
[証明]. .ベクトル hp+1R を展開した行列の対角要素 hp+1Rm は(4.45)の被積分関数を Newton の補間公式で表した式の t=t0+mh における剰余項に同じである。(4.45)の積分変数 x, z を x=t0+rh 及び z=t0+qh となる r, q に変換すると、
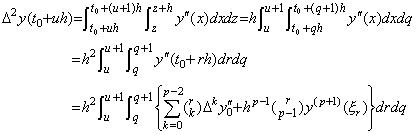
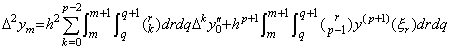 ___(4.54)
___(4.54)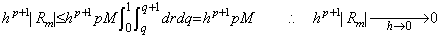
| [Q.E.D.] |
. .従って、(4.52)の行列を D−2 で表すと、2重積分は次のように表される。
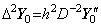 _______(4.55)
_______(4.55)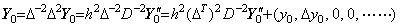 ___(4.56)
___(4.56). . 初期値 y0' は微分 Y0' =h−1DΔY0 の行列演算式の第1行で表される。即ち、
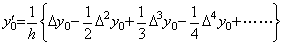 _____(4.57)
_____(4.57). . 行列演算式(4.55)は(4.52)に示すように被積分関数の t0 から tp−2 迄を積分して t0 から tp 迄の結果を得る。故に、演算子 h2D−2 は p−1 次の行列であり、tp−2 から tp 迄の2区間を予測する予測子である。一方、行列演算式(4.56)は被積分関数が y0" から Δpy0" 迄の p+1 要素を持つベクトルで表され得るならその t0 から tp 迄を積分して t0 から tp 迄の結果を得る。行列
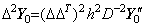 _______(4.58)
_______(4.58). .[定理 4.16]. .次の関係は剰余項に無関係に常に成立する。
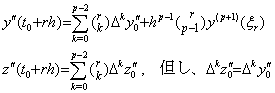
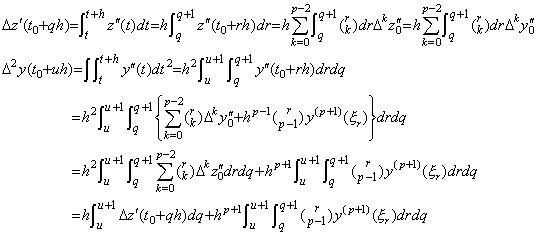
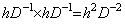 _____________[Q.E.D.]
_____________[Q.E.D.]. . 従って、h2D−2 による2重積分は hD−1 による2回の積分と等価である。後者の場合、単積分のプログラムを2回使うことができ、初期値 y0' を(4.57)により階差 Δy0 に変換する必要はない。何故なら、階差 Δy0 は ΔY0=hD−1Y0' で表される2回目の積分で初期値 y0' を用いて得られるからである。しかし、それは前者の場合の2倍の計算時間を必要とし、定理 4.16 が D−1の要素の丸め誤差のため正確に成立しないことにより結果の精度が多少失われる場合もあり得る。
4.7 n 重責分演算子
. .
導関数 y' (t) は y(t)−y0 の微分により得られ、2次導関数 y"(t) は y' (t)−y0' の微分により得られる。同様に、n 次導関数は
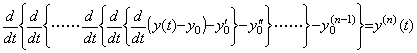 ___(4.60)
___(4.60)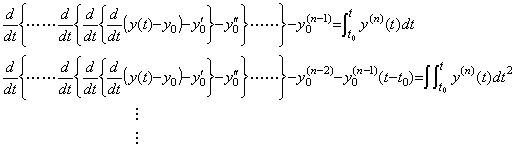
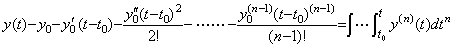 ____(4.61)
____(4.61)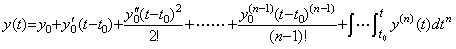 ___(4.62)
___(4.62)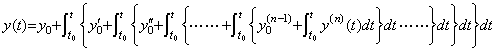 ___(4.63)
___(4.63). .[定理 4.17]. .関数が y(t)∈Cp[a, b] なら以下を満たす ξ が存在する。
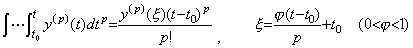 _____(4.64)
_____(4.64)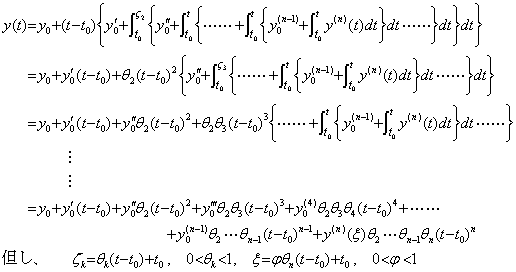
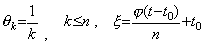
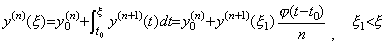
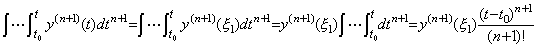
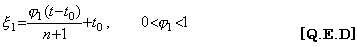
. . n 重積分演算子を導くためには、(4.61)は先ず y(t) 及び y(n)(t) の逐次階差を用いた行列演算式で表されなければならない。従って、初期値は y(t) 及び y(n)(t) の両ベクトルの要素ではないから全て消去されねばならない。
. .[定理 4.18]. .(4.61)から全ての初期値を消去すると、
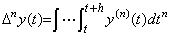 ________(4.65)
________(4.65)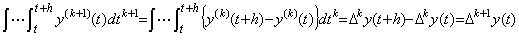
| [Q.E.D.] |
. . [定理 4.19]. .整数 m が m≥0 なら Δm+ny(t) は次のようになる。
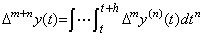 ________(4.66)
________(4.66)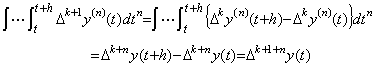
| [Q.E.D.] |
. . [定理 4.20]. . y(n)(t)∈Cp−n+1[a, b] のとき、それを Newton の剰余項付き補間公式で表すと、t0 から t 迄の n 重積分の逐次階差は次のようになる。但し、0≤m≤p−n である。
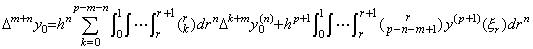 ____(4.67)
____(4.67)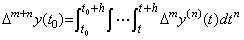
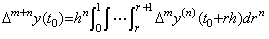 ________(4.68)
________(4.68)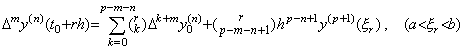
| [Q.E.D.] |
. . [定理 4.21]. .整数 m 及び n が 0≤m<n を満たすとき、
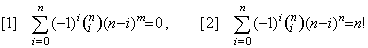 _____(4.69)
_____(4.69)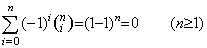
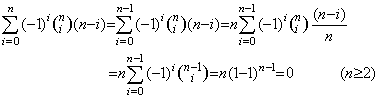
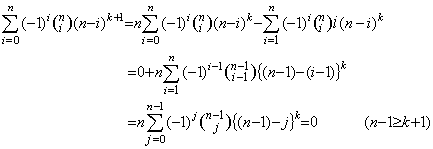
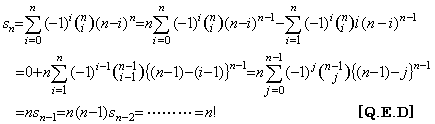
. . [定理 4.22]. .(4.67)の Δk+my0(n) の係数を akn と表すと、
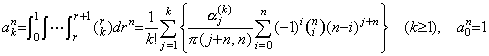 _____(4.70)
_____(4.70)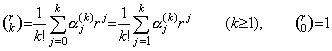 ______(4.71)
______(4.71)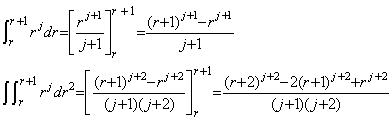
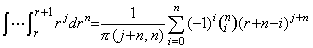 _____(4.72)
_____(4.72)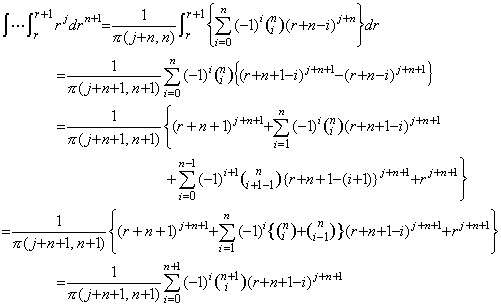
| [Q.E.D.] |
. .
定理 4.20 及び 4.22 により、導関数 y(n)(t) のベクトルと Δny(t) のベクトルの関係は(4.67)の 0≤m≤p−n の各式を並べて次の行列演算式で表すことができる。
 __(4.73)
__(4.73)但し、. .
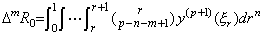
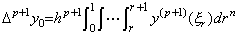 ______(4.74)
______(4.74)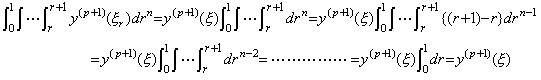
. .[定理 4.23]. .両関数 y(t) 及び g(t) が連続で、t0 から t の区間で符号を変えないなら、次の関係を満たす値 ξ が存在する。
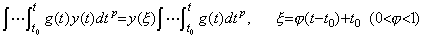 ____(4.75)
____(4.75)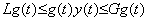
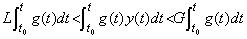
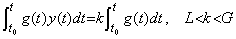
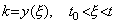
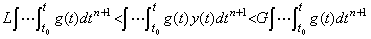
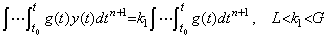
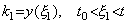
g(t)<0 が負の場合も同様にして証明される。______[Q.E.D.]
. . 剰余項 ΔmR0 の一番内側の積分を f(r) で表すと、定理 4.17 により次式を満たす u が存在する。
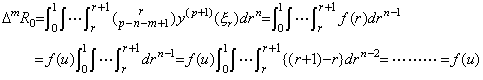
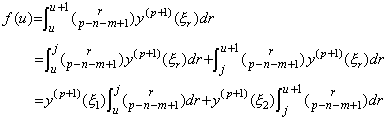
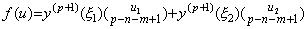
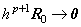
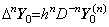 ______(4.76)
______(4.76)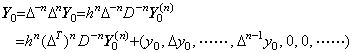 _____(4.77)
_____(4.77). . この変換は著者がこの演算子法を発見した切っ掛けであった。この変換はこの演算子法に類似の行列演算式で表されるが、その行列はこの演算子法の演算子ではない。何故なら、その被演算子は要素が逐次階差ではなく、初期値点における逐次微分値であるベクトルだからである。この行列は通常の数値計算をこの演算子法に結び付ける演算子である。その詳細は第四章で述べる。
. . (4.76)の演算子 hnD−n は行列 D−n が p−n+1 次であるから t0 から tp−n 迄の被演算子を用いて t0 から tp 迄の n 重積分を得る。故に、これは tp−n から tp 迄の n 重積分を予測する予測子である。(4.77)の行列 D−n が p+1 次のとき、(4.77)に左から Δn を掛けると、
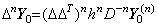 ________(4.78)
________(4.78). .[定理 4.24]. .次の関係は剰余項の有無にかかわらず常に成立する。
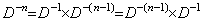 _______(4.79)
_______(4.79)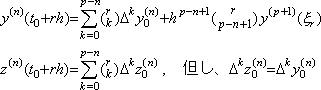
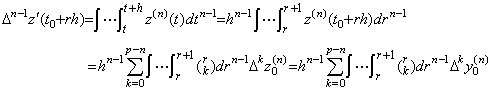
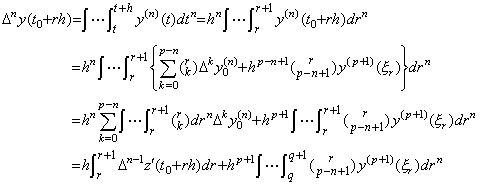
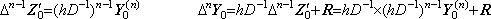
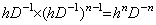
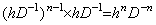 ________[Q.E.D.]
________[Q.E.D.]. . 従って、n 重積分は単積分プログラムを n 回使って行っても良い。その場合は y0' から y0(n−1) 迄の初期値を Δy0 から Δn−1y0 迄の逐次階差に変換する必要はない。何故なら、逐次積分は次のようになるからである。
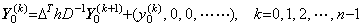 _____(4.80)
_____(4.80)