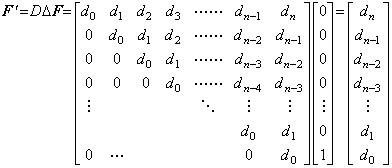|
4.. .積分演算子の導入
4.1. .積分演算子の概略
. .
微分可能関数 y(t) は y(t0) を y0 で表すと、導関数 y' (t) の t0 から t 迄の積分で次のように表される。
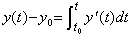 ______(4.1)
この逐次階差は等間隔区分点 t=t0+qh における値を用いて次のように求められる。 ______(4.1)
この逐次階差は等間隔区分点 t=t0+qh における値を用いて次のように求められる。
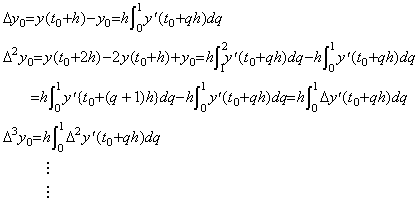 . .
h の値が非常に小さいとき、これらの被積分関数は 0≤q≤1 に対しては定数 y0', Δy0', Δ2y0', ……… に殆ど等しい。従って、(4.1)はある行列を A で表すと行列演算式 ΔY=hAY ' で表すことが出来る。(4.1)の左辺の t=t0 における値 y0 は積分演算の結果ではないからこの行列演算式には現れない。積分は関数ではないから行列 A はベクトルの行列展開ではない。ベクトルの形式を持たない商か、商でない演算子である。故に、行列 A をただ1つの関数の ΔY 及び Y ' により計算することは出来ない。全ての微分可能関数及びその1次導関数のベクトルを用いて計算しなければならない。
. .
h の値が非常に小さいとき、これらの被積分関数は 0≤q≤1 に対しては定数 y0', Δy0', Δ2y0', ……… に殆ど等しい。従って、(4.1)はある行列を A で表すと行列演算式 ΔY=hAY ' で表すことが出来る。(4.1)の左辺の t=t0 における値 y0 は積分演算の結果ではないからこの行列演算式には現れない。積分は関数ではないから行列 A はベクトルの行列展開ではない。ベクトルの形式を持たない商か、商でない演算子である。故に、行列 A をただ1つの関数の ΔY 及び Y ' により計算することは出来ない。全ての微分可能関数及びその1次導関数のベクトルを用いて計算しなければならない。
. .
導関数が定数、即ち、y' (t)=c1 なら(4.1)は y(t)−y0=c1t となり、その逐次階差は Δy0=c1h だけである。従って、行列演算式は c1h1=hAc11 となる。これはこの行列の第1列は第1要素が1である他は全ての要素が零であることを必要とする。
. .
導関数が y' (t)=c1+2c2t なら(4.1)は y(t)−y0=c1t+c2t2 になる。従って、行列演算式は次のようになり、この行列の第2列は a12=1/2, a22=1 及びその他の要素は全て零であることを必要とする。
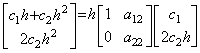 . .
導関数が y' (t)=c1+2c2t+3c3t2 なら(4.1)は y(t)−y0=c1t+c2t2+c3t3 になる。従って、 . .
導関数が y' (t)=c1+2c2t+3c3t2 なら(4.1)は y(t)−y0=c1t+c2t2+c3t3 になる。従って、
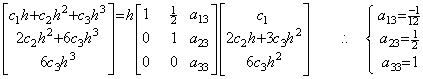 . .
同様の操作を繰り返すと、第1行が次に示すものであり、その他の行は1行上の行の要素を1要素右へシフトしたものである三角行列 A を得る。
. .
同様の操作を繰り返すと、第1行が次に示すものであり、その他の行は1行上の行の要素を1要素右へシフトしたものである三角行列 A を得る。
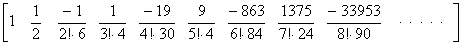 . .
この行列は微分行列 D の逆行列である。従って、(4.1)の積分は次のように表せる。
. .
この行列は微分行列 D の逆行列である。従って、(4.1)の積分は次のように表せる。
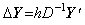 _______(4.2)
しかし、この行列が全ての積分可能関数に対して成立することを証明するのは困難である。積分結果の関数が p+1 回連続微分可能関数であるなら、その証明は Newton の剰余項付き補間公式とその積分を用いて行うことが出来る。それについては次節以降で示す。 _______(4.2)
しかし、この行列が全ての積分可能関数に対して成立することを証明するのは困難である。積分結果の関数が p+1 回連続微分可能関数であるなら、その証明は Newton の剰余項付き補間公式とその積分を用いて行うことが出来る。それについては次節以降で示す。
. .
著者は 3.5 節において微分演算子は Δh−1D であると述べた。しかし、被演算子を ΔY とすれば微分演算子は h−1D となり、(4.2)が微分演算の逆演算となる。この考えは従来の微分演算子の問題点を解決するであろう。関数が定数であるなら、被演算子は ΔY =0 であるから微分結果は Y ' =0 となる。
. .
従来の微分演算においても、それが(4.1)の逆演算であるべきである。従って、微分演算の被演算子は y(t)−y0 であるべきである。微分の定義は(4.3)で表される。
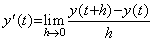 _______(4.3)
関数 y(t) が定数のとき導関数 y' (t) は任意の h の値に対して零になる。これは演算子 lim の被演算関数が恒等的に零であるからである。更に、上記の定義は(4.4)の略式定義であると考えることが出来、微分演算の被演算関数も y(t)−y0 であり、恒等的に零である。 _______(4.3)
関数 y(t) が定数のとき導関数 y' (t) は任意の h の値に対して零になる。これは演算子 lim の被演算関数が恒等的に零であるからである。更に、上記の定義は(4.4)の略式定義であると考えることが出来、微分演算の被演算関数も y(t)−y0 であり、恒等的に零である。
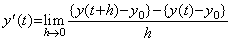 ______(4.4)
. .
従来の定義では、積分演算は任意の定数 c を加算する演算を含んでおり、(4.5)で表される。 ______(4.4)
. .
従来の定義では、積分演算は任意の定数 c を加算する演算を含んでおり、(4.5)で表される。
 ______(4.5)
この場合、不定定数を加算する演算は t=t0 においても行われるから y(t0) の値は積分演算(4.5)の結果である。従って、積分演算子はこの加算演算子を含んだ混成演算子と考えなければならない。本演算子法では、この積分結果のベクトル Y はこの定数を第1要素として持つ。その演算は(4.2)に ΔT を掛け、定数ベクトル c1 を加えることにより、次のように行列演算式で表される。 ______(4.5)
この場合、不定定数を加算する演算は t=t0 においても行われるから y(t0) の値は積分演算(4.5)の結果である。従って、積分演算子はこの加算演算子を含んだ混成演算子と考えなければならない。本演算子法では、この積分結果のベクトル Y はこの定数を第1要素として持つ。その演算は(4.2)に ΔT を掛け、定数ベクトル c1 を加えることにより、次のように行列演算式で表される。
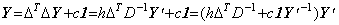 ____(4.6)
この積分演算子は不定な演算子を持つ。それはベクトルではなく、形式的に括弧内の第2項で表される。 ____(4.6)
この積分演算子は不定な演算子を持つ。それはベクトルではなく、形式的に括弧内の第2項で表される。
. .
定数が y0=y(t0) であるなら(4.5)は微分方程式の解になる。この場合には、定数ベクトル y01 は定数 y0 が微分する前のベクトル Y の第1要素であることを示す厳密な形式で表されなければならない。それは第 2.4 節の和演算子で述べた第1行1列が1である行列単位 U0 により U0Y と表される。従って、(4.6)は第 2.4 節で定義された Δ−1 を用いて厳密な形式で表される。
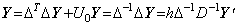 ______(4.7). .
微分演算子 h−1D は初期値 y0 を持たない被演算子 ΔY に対して作用する。従って、初期値には作用しない。この逆演算子は hD−1 であり、その演算結果は一意に ΔY である。微分演算子 Δh−1D は演算子 h−1D と同じ導関数を与える。しかし、被演算子がベクトル Y であるから初期値 y0 に作用する。この演算子はベクトル Y を微分方程式に変換する。従って、初期値はそのまま保持され、微分方程式と共に記述されなければならない。この逆演算子は hΔ−1D−1 であり、それによる結果は一意に Y である。 ______(4.7). .
微分演算子 h−1D は初期値 y0 を持たない被演算子 ΔY に対して作用する。従って、初期値には作用しない。この逆演算子は hD−1 であり、その演算結果は一意に ΔY である。微分演算子 Δh−1D は演算子 h−1D と同じ導関数を与える。しかし、被演算子がベクトル Y であるから初期値 y0 に作用する。この演算子はベクトル Y を微分方程式に変換する。従って、初期値はそのまま保持され、微分方程式と共に記述されなければならない。この逆演算子は hΔ−1D−1 であり、それによる結果は一意に Y である。
. .
通常の微分演算はこの2つの演算を区別しないから問題が生ずる。その問題は(4.3)と(4.4)の定義を区別することにより解決する。導関数 y' (t) は(4.4)で定義されるべきであり、従って、この微分は d(y-y0)/dt と表され、その逆演算は(4.1)で表される。(4.3)の定義は dy/dt と表されるが、この微分演算は初期値 y0 にも作用する。但し、その値を変えることなく、導関数との対を構成する、即ち、関数 y(t) を微分方程式に変換する。その逆変換は c=y(t0) として(4.5)で表される。
. .
ラプラス変換は次に示すように微分演算子を L{y(t)−y(0)} に対する演算として定義する。ここで記号 L はラプラス変換を表す。
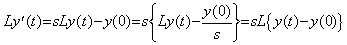 従って、その逆変換は L{y(t)−y(0)} を与えなければならない。しかし、ラプラス変換は次に示すように sLy(0) を反対側に移項して両辺に s−1 を掛ける。
従って、その逆変換は L{y(t)−y(0)} を与えなければならない。しかし、ラプラス変換は次に示すように sLy(0) を反対側に移項して両辺に s−1 を掛ける。
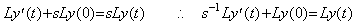 これは t0=0 及び c=y(0) の(4.5)に同じである。演算子 s と s−1 の間のこれらの関係は通常の定義では明示的に示されない。
これは t0=0 及び c=y(0) の(4.5)に同じである。演算子 s と s−1 の間のこれらの関係は通常の定義では明示的に示されない。
. .
ユニットステップ関数を u(t) で表して、全ての関数及び導関数は y(t)u(t), y' (t)u(t), y"(t)u(t), ………, y(n)(t)u(t) によって定義されていると仮定すると、この2つの微分演算を区別する必要はなくなる。何故なら、微分演算は初期値 y0 を連続微分可能なインパルス関数 y0δ(t) として保持するからである。但し、このインパルス関数は第2章 3.2 節で述べたものであり、Dirac のデルタ関数ではない。ラプラス変換はこれらの関数を扱うのであるが、通常はこれらの関数の表記から u(t) を省略する。この u(t) を明示的に表記する厳密なラプラス変換は第2章 3.4 節の任意の関数のラプラス変換で述べてある。
. .
Mikusinski の演算子法もこれらの関数を扱うが、関数を {y(t)}, {y' (t)}, {y"(t)}, …… で表し、インパルス関数 y0δ(t) を数演算子 y0 として表す。微分及び積分演算は以下の数式に等価である。
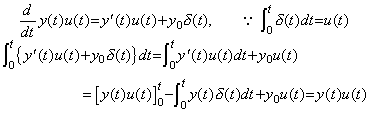 (d/dt)y(t)u(t) が恒等的に零なら被演算関数 y(t)u(t) が恒等的に零である。導関数 y' (t)u(t) は y0δ(t) を左辺へ移項することにより得なければならない。故に、この場合にも、微分演算の被演算関数は y(t)u(t)−y0u(t) になる。
(d/dt)y(t)u(t) が恒等的に零なら被演算関数 y(t)u(t) が恒等的に零である。導関数 y' (t)u(t) は y0δ(t) を左辺へ移項することにより得なければならない。故に、この場合にも、微分演算の被演算関数は y(t)u(t)−y0u(t) になる。
. .
著者の演算子法は u(t) が t=0 において立ち上がる現象を表せない Newton の補間公式に基づいている。従って、この2つの微分演算及びそれらの逆演算は区別されなければならない。演算子 hΔ−1D−1 が理論的には微分方程式の解を与える。しかし、実際の計算では Δ を両辺に掛けることにより(4.7)を(4.2)に変換し、ΔY を求めた後に(4.7)の Y=ΔTΔY+U0Y により解 Y を求める。
4.2. .Newton の補間公式の積分
. .
微分演算子の導入において、著者は p+1 回連続微分可能関数の微分を扱った。積分演算子の導入においては、積分は微分演算の逆演算であるから、被積分関数は p 回連続微分可能関数でなければならない。従って、この節では第 3.4 節の Newton の補間公式(3.21)で表された y' (t) の積分公式を求める。通常の積分公式は f(t)∈Cp+1[a, b] である関数 f(t) の Newton の補間公式を用いて表される。その公式は p+1 及び f をそれぞれ p 及び y' に代入すれば得られ、その結果の y(t) は p+2 回連続微分可能関数となる。
. .
[定理 4.1]. .y' (t)∈Cp[a, b] であるとき、任意の整数 m に対して tm=t0+mh で表される等間隔区分点の tm から tm+1 迄を積分すると、
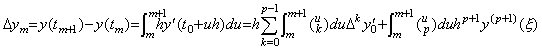 ____(4.8)
但し、 ξ は y' (t) の m<q<m+1 なる q に対する補間の剰余を与えるある値である。 ____(4.8)
但し、 ξ は y' (t) の m<q<m+1 なる q に対する補間の剰余を与えるある値である。
[証明]. .t=t0+uh を代入すると、
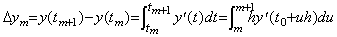 第 3.4 節に述べたように、導関数 y' (t) を(3.22)で表すと、その近似公式が、ある q の値に対する(3.22)の剰余項の R の値である Rq を定数として持つとき残差 F(u) は(3.23)で表される。これらを以下に示す。
第 3.4 節に述べたように、導関数 y' (t) を(3.22)で表すと、その近似公式が、ある q の値に対する(3.22)の剰余項の R の値である Rq を定数として持つとき残差 F(u) は(3.23)で表される。これらを以下に示す。
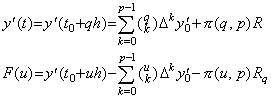 q の値が m<q<m+1 を満たすとき残差 F(u) は範囲 [m, m+1] の近辺でおおよそ第 3.2 節の Fig 3.1 で表される。従って、残差 F(u) の m から m+1 迄の積分が零になるある値 q が存在し、そのときの剰余項の R の値 Rq を定数として剰余項に持つ近似公式が存在する。その場合に、
q の値が m<q<m+1 を満たすとき残差 F(u) は範囲 [m, m+1] の近辺でおおよそ第 3.2 節の Fig 3.1 で表される。従って、残差 F(u) の m から m+1 迄の積分が零になるある値 q が存在し、そのときの剰余項の R の値 Rq を定数として剰余項に持つ近似公式が存在する。その場合に、
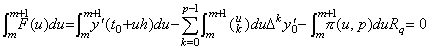 ____(4.9)
この q に対して F(p)(u)=0 を満たす ξ=t0+uh が存在する。従って、 ____(4.9)
この q に対して F(p)(u)=0 を満たす ξ=t0+uh が存在する。従って、
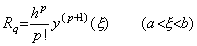 故に、(4.9)に h を掛ければ(4.8)が得られる。_________[証明終]
故に、(4.9)に h を掛ければ(4.8)が得られる。_________[証明終]
. .
[定理 4.2]
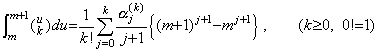 ____(4.10)
[証明]. .定理 3.27 により、 ____(4.10)
[証明]. .定理 3.27 により、
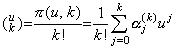 ______且つ______ ______且つ______
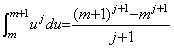 | [証明終] |
. .
(4.8)に m=0 を代入すれば Δy0 、即ち、剰余項付き Newton の補間公式の t0 から t0+h 迄の積分を得る公式である。その各項の係数は(4.10)に m=0 を代入した(4.11)で表され、ak で表される。
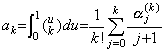 ______(4.11)
右辺の総和は第 3.7 節の Table 3.3 に示した行列と次に示すようにその要素が 1/(j+1) である縦ベクトルの積を意味する。但し、行列は Table 3.3 の空の欄の要素には全て零を持つ。 ______(4.11)
右辺の総和は第 3.7 節の Table 3.3 に示した行列と次に示すようにその要素が 1/(j+1) である縦ベクトルの積を意味する。但し、行列は Table 3.3 の空の欄の要素には全て零を持つ。
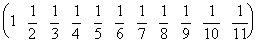 従って、k=0 から 10 迄の係数 ak は次のようになる。
従って、k=0 から 10 迄の係数 ak は次のようになる。
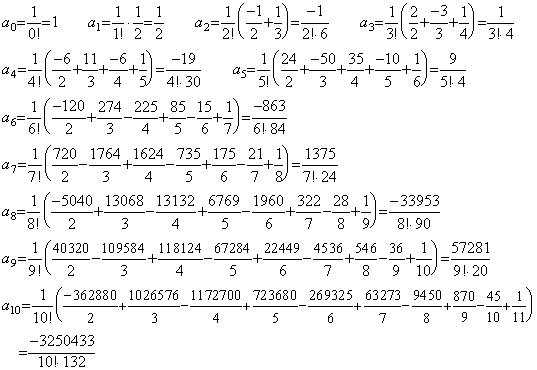
. .
故に、m=0 のとき(4.8)は(4.12)になる。但し、ξ0 は 0<q<1 なる q の値に対する ξ を示す。
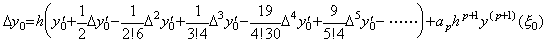 ____(4.12)
m≥1 の場合も、(4.8)の係数を(4.10)及び Table 3.3 を用いて計算することが出来る。しかし、次の定理を用いる方が簡単である。 ____(4.12)
m≥1 の場合も、(4.8)の係数を(4.10)及び Table 3.3 を用いて計算することが出来る。しかし、次の定理を用いる方が簡単である。
. .
[定理 4.3]
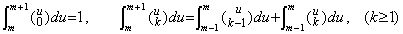 ____(4.13)
[証明]. .k=0 なら、 ____(4.13)
[証明]. .k=0 なら、
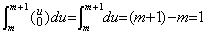 k≥1 なら u−1=v の代入により、
k≥1 なら u−1=v の代入により、
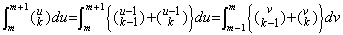 |
[証明終] |
. .
従って、n≥2 のとき、(4.8)で表される Δy1 の n 番目の係数は Δy0 の n−1 番目と n 番目の係数の和により得られる。同様に、Δy2 の係数も Δy1 の係数を用いて得られる。従って、(4.12)から始めて [t0, t1] から [tp−1, tp] 迄の等間隔区間の p 個の積分公式が次々と得られる。
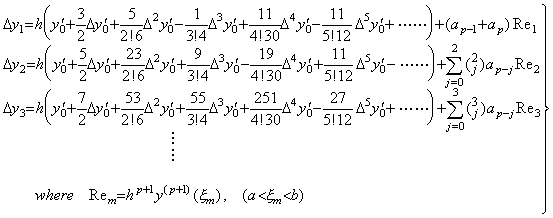 (4.14) (4.14)
4.3 シンプソンの1/3則の剰余項
. .
(4.9)の積分区間を t0 から t2 迄の2区間に代えると、
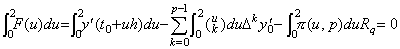 ____(4.15) ____(4.15)
但し、 ____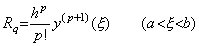 故に、Newtorn の補間公式を t0 から t2 迄積分する公式は次のようになるであろう。
故に、Newtorn の補間公式を t0 から t2 迄積分する公式は次のようになるであろう。
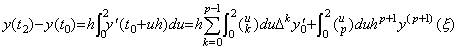 _____(4.16)
右辺の積分で表された係数は(4.10)の積分範囲を m から m+2 迄の2区間に代え、m に零を代入すれば得られる。従って、 _____(4.16)
右辺の積分で表された係数は(4.10)の積分範囲を m から m+2 迄の2区間に代え、m に零を代入すれば得られる。従って、
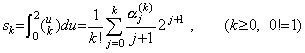 第 3.7 節 Table 3.3 の第1種 Stirling 数を用いると sk の値は次のようになる。
第 3.7 節 Table 3.3 の第1種 Stirling 数を用いると sk の値は次のようになる。
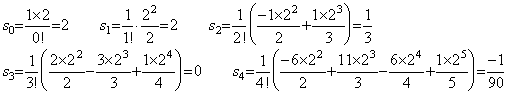 従って、(4.16)は p=4 の場合に剰余項付き Simpson の 1/3 則になる。
従って、(4.16)は p=4 の場合に剰余項付き Simpson の 1/3 則になる。
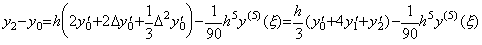 ____(4.17)
通常は被積分関数は導関数で表さないので y' を f で表すと剰余項は y(5)(ξ) の代りに f(4)(ξ) で表される。 ____(4.17)
通常は被積分関数は導関数で表さないので y' を f で表すと剰余項は y(5)(ξ) の代りに f(4)(ξ) で表される。
. .
これは Simpson の 1/3 則の剰余項としてよく知られているが、厳密に言えばこれは正しくない。(4.17)に示すように Simpson の 1/3 則は第3階差の影響を受けない。従って、3次導関数が連続微分可能でない関数 f(t) にも適用できる。この場合、上記の剰余項が正しい値を与える ξ は存在しない。例えば、関数が(4.18)であるとする。
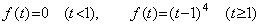 _____(4.18)
t=0 から 2 迄の積分値、 h=1 による Simpson の 1/3 則の値、正しい剰余の値、(4.17)の剰余項の値は次のようになる。 _____(4.18)
t=0 から 2 迄の積分値、 h=1 による Simpson の 1/3 則の値、正しい剰余の値、(4.17)の剰余項の値は次のようになる。
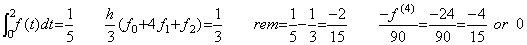 従って、−f(4)/90=−2/15 が満たされる ξ の値は存在しない。関数 f(t) が t<1 においても (t−1)4 であるなら剰余項が正しい値を与える ξ の値は存在する。
従って、−f(4)/90=−2/15 が満たされる ξ の値は存在しない。関数 f(t) が t<1 においても (t−1)4 であるなら剰余項が正しい値を与える ξ の値は存在する。
. .
この問題点の原因は 4 次導関数が連続であり、且つ、(4.15)に示す残差の積分が満たされるような 1 点 q が存在するという仮定である。剰余項に関する従来の証明は全てこの仮定を用いている。4 次導関数が連続であっても、2 区間の積分の場合は残差 F(u) の積分が零になる 1 点 q は存在しない。その理由は次の通りである。
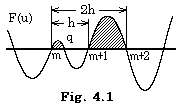 . .
残差 F(u) は u=q において零になり、|u−q| の増加と共にその絶対値を増加する。何故なら、定数 Rq と任意の u に対する R の真の値との差は増加するからである。しかし、それは π(u, p) を掛けられるので等間隔区分点では零になる。故に、残差 F(u) の曲線はおよそ Fig. 4.1 に示されるようになる。その振幅は点 q がある区間で最小であり、それより離れた区間では大きくなる。従って、F(u) の 1 区間の積分では積分値が零となる q が確かに存在するが、2 区間の積分の場合にはそのような q は存在しない。3 区間の積分の場合には、そのような q が存在するかもしれないが確実ではない。4 区間の積分の場合には、そのような q は存在しないであろう。 . .
残差 F(u) は u=q において零になり、|u−q| の増加と共にその絶対値を増加する。何故なら、定数 Rq と任意の u に対する R の真の値との差は増加するからである。しかし、それは π(u, p) を掛けられるので等間隔区分点では零になる。故に、残差 F(u) の曲線はおよそ Fig. 4.1 に示されるようになる。その振幅は点 q がある区間で最小であり、それより離れた区間では大きくなる。従って、F(u) の 1 区間の積分では積分値が零となる q が確かに存在するが、2 区間の積分の場合にはそのような q は存在しない。3 区間の積分の場合には、そのような q が存在するかもしれないが確実ではない。4 区間の積分の場合には、そのような q は存在しないであろう。
. .
しかしながら、点 m+1 に関して点 q に対称な点 q' においても残差 F(u) が零になる場合には残差 F(u) の 2 区間の積分値が零になる q が存在する。逆に言えば、残差 F(u) の 2 区間の積分値が零になる q が存在するなら、点 m+1 に関して点 q に対称な点 q' においても残差 F(u) が零になるのである。従って、被積分関数 y' の補間公式の剰余項は区分点 t0 から tp−1 迄の p 点及び q と q' の p+2 点で零になり、(4.15)の剰余項の被積分関数 π(u, p) は π(u, p+1) に代わり、Σ の上限、及び、剰余項の定数 Rq を与える式の p も p+1 に代わる。但し、y' は p 回ではなく p+1 回連続微分可能でなければならない。2 区間の積分公式(4.16)の p も p+1 に代わり、2 区間の積分公式は(4.19)となる。
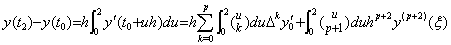 ____(4.19)
Simpson の 1/3 則は p=4 ではなく p=3 の場合であり、階差は係数が s3=0 であるから第 2 階差迄であり、剰余項は p+1=4, p+2=5 であるから s4h5y(5)(ξ) となり、結局(4.17)と同じになる。y' を f で表せば剰余項は f(4)(ξ) で表される。又、3 点による近似では被積分関数にも積分結果の関数にも第 3 階差は存在しないのである。 ____(4.19)
Simpson の 1/3 則は p=4 ではなく p=3 の場合であり、階差は係数が s3=0 であるから第 2 階差迄であり、剰余項は p+1=4, p+2=5 であるから s4h5y(5)(ξ) となり、結局(4.17)と同じになる。y' を f で表せば剰余項は f(4)(ξ) で表される。又、3 点による近似では被積分関数にも積分結果の関数にも第 3 階差は存在しないのである。
. .
しかし、この場合にも問題点が存在する。この剰余項は残差関数 F(u) の剰余項の定数 Rq により与えられるが、その定数は(4.15)の Rq の p を p+1 に代え、p=3 を代入したものである。従って、残差関数は(4.20)になる。
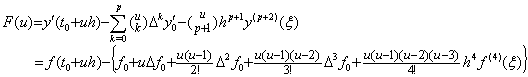 ___(4.20)
被積分関数が t≥0 において f(t)=t4 のとき、t=0 から 2 迄の積分、区分幅 h=1 による剰余項なしの Simpson の 1/3 則の値、それから求めた剰余項の値、定数 Rq の値、各階差、残差関数 F(u) は以下のようになる。 ___(4.20)
被積分関数が t≥0 において f(t)=t4 のとき、t=0 から 2 迄の積分、区分幅 h=1 による剰余項なしの Simpson の 1/3 則の値、それから求めた剰余項の値、定数 Rq の値、各階差、残差関数 F(u) は以下のようになる。
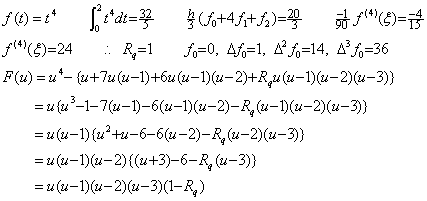 残差関数は区分点 u=0, 1, 2 の他に積分範囲の外の u=3 で零になるが、もう1点が存在しない。この場合には、f(4)(t) が定数関数であり、Rq の値がどこでも定数 1 であるから F(u) は恒等的に零であるので問題ない。
残差関数は区分点 u=0, 1, 2 の他に積分範囲の外の u=3 で零になるが、もう1点が存在しない。この場合には、f(4)(t) が定数関数であり、Rq の値がどこでも定数 1 であるから F(u) は恒等的に零であるので問題ない。
. .
被積分関数が f(t)=t5 のとき、t=0 から 2 迄の積分、剰余項なしの Simpson の 1/3 則の値、剰余項の値、定数 Rq の値、各階差、残差関数 F(u) は以下のようになる。
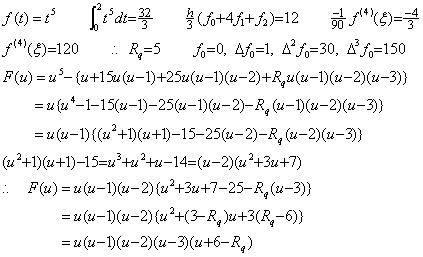 残差関数は 6−Rq=1 であるから区分点の3点の他に u=3 と u=−1 の2点で零になる。関数 (u−3)(u+1) は u=1+q を代入すると (u−3)(u+1)=(q−2)(q+2) となり、これは直線 q=0 即ち、直線 u=1 に対して対称である。これと、点 u=1 に対して点対称な関数 u(u−1)(u−2) との積である F(u) は点 u=1 に対して点対称であるから F(u) の u=0 から u=2 迄の積分が零になることは明らかである。点 u=3 は Simpson の 1/3 則では使用されていないが証明の過程で使用しているからこの点で残差が零になるのは当然であり、この点と中点 u=1 に対して対称な点 u=−1 においても残差は零になるのである。しかし、この2点が積分範囲の内部にあるという仮定と矛盾する。これは2区間の積分では、積分区間内で F(q)=0 となり、残差 F(u) の積分が零になるような、区分点以外の点 q は存在しないことを示す。
残差関数は 6−Rq=1 であるから区分点の3点の他に u=3 と u=−1 の2点で零になる。関数 (u−3)(u+1) は u=1+q を代入すると (u−3)(u+1)=(q−2)(q+2) となり、これは直線 q=0 即ち、直線 u=1 に対して対称である。これと、点 u=1 に対して点対称な関数 u(u−1)(u−2) との積である F(u) は点 u=1 に対して点対称であるから F(u) の u=0 から u=2 迄の積分が零になることは明らかである。点 u=3 は Simpson の 1/3 則では使用されていないが証明の過程で使用しているからこの点で残差が零になるのは当然であり、この点と中点 u=1 に対して対称な点 u=−1 においても残差は零になるのである。しかし、この2点が積分範囲の内部にあるという仮定と矛盾する。これは2区間の積分では、積分区間内で F(q)=0 となり、残差 F(u) の積分が零になるような、区分点以外の点 q は存在しないことを示す。
. .
従来、剰余項付き Simpson の 1/3 則の証明は被積分関数が剰余項付き 3 次の Taylor 展開で表されることを仮定している。しかし、区分点が3点だけでは 3 次関数は確定しない。積分結果に 3 次の項が影響しないから差支えないという考えは間違いであることを上の結果は示している。実際には、明示することなく第4点 u=3 を用いて3区間で3次関数を確定し、その2区間を積分しているのであり、(4.19)の被積分関数が第4点を使用しているのと同じである。2区間の積分は1区間毎の積分の和と一致しなければならない。しかし、Simpson の 1/3 則の従来の剰余項はこれと一致しない。4区分点を用いた3区間の最初の1区間の積分は(4.12)で p=4 及び y'=f と置けば次のようになる。
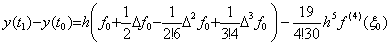 ____(4.21)
区分幅を h=1 として f(t)=t4 の場合の剰余項の定数 Rq 及び残差関数 F(u) を求めれば次のようになり、Rq=1 であるから F(u) は恒等的に零になる。 ____(4.21)
区分幅を h=1 として f(t)=t4 の場合の剰余項の定数 Rq 及び残差関数 F(u) を求めれば次のようになり、Rq=1 であるから F(u) は恒等的に零になる。
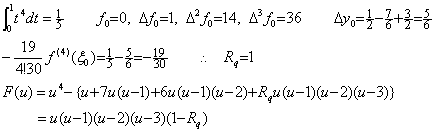 ____
f(t)=t5 の場合には、次に示すように Rq=5 であるから最初の区間の略中央 u=0.447… で F(u)=0 となることが確認できる。 ____
f(t)=t5 の場合には、次に示すように Rq=5 であるから最初の区間の略中央 u=0.447… で F(u)=0 となることが確認できる。
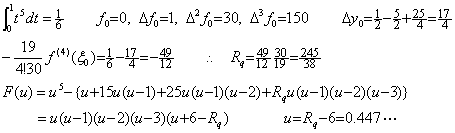 ____
3区間の2番目の区間の積分は(4.14)の第一式より次の(4.22)となる。 ____
3区間の2番目の区間の積分は(4.14)の第一式より次の(4.22)となる。
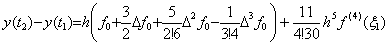 ____(4.22)
f(t)=t4 の場合のこの区間の積分の剰余項の定数 Rq は近似積分の誤差から求めなくても、f(4)(t)≡4! で定数であるから Rq=1 であり、残差関数 F(u) は恒等的に零になる。 f(t)=t5 の場合の Rq 及び残差関数 F(u) は次のようになり、第2区間の中央 u=1.5 で F(u)=0 となることが確認できる。 ____(4.22)
f(t)=t4 の場合のこの区間の積分の剰余項の定数 Rq は近似積分の誤差から求めなくても、f(4)(t)≡4! で定数であるから Rq=1 であり、残差関数 F(u) は恒等的に零になる。 f(t)=t5 の場合の Rq 及び残差関数 F(u) は次のようになり、第2区間の中央 u=1.5 で F(u)=0 となることが確認できる。
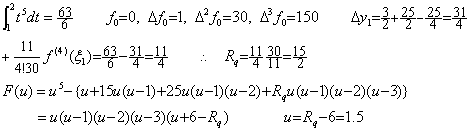 . .
2区間の積分はこの両者の和であり、上記の(4.21)と(4.22)を加えれば Simpson の 1/3 則が得られるが、剰余項は(4.17)の剰余項と一致しない。(4.21)の剰余項の f(4)(ξ0) は区間[0, 1]で F(u)=0 となる点 q=0.447… における被積分関数 f(t) の剰余項を与える値であり、(4.22)の剰余項の f(4)(ξ1) は区間[1, 2]で F(u)=0 となる点 q=1.5 における被積分関数 f(t) の剰余項を与える値であり、両者は一般的には等しくないからである。被積分関数が y'(t)=f(t)=t4 で f(4)(t) が定数である場合のように、両者が等しい場合には(4.17)の剰余項が成立する。そのような場合に限り Simpson の 1/3 則の従来の剰余項は成立するのである。しかし、更に厳密に言えば、2区間の積分はその2区間で確定する被積分関数を使用し、残差関数 F(u) の積分が零になることが確実である一区間毎の積分結果を加算して求めなければならない。従って、剰余項付き Simpson の 1/3 則は以下のように求めなけばならない。 . .
2区間の積分はこの両者の和であり、上記の(4.21)と(4.22)を加えれば Simpson の 1/3 則が得られるが、剰余項は(4.17)の剰余項と一致しない。(4.21)の剰余項の f(4)(ξ0) は区間[0, 1]で F(u)=0 となる点 q=0.447… における被積分関数 f(t) の剰余項を与える値であり、(4.22)の剰余項の f(4)(ξ1) は区間[1, 2]で F(u)=0 となる点 q=1.5 における被積分関数 f(t) の剰余項を与える値であり、両者は一般的には等しくないからである。被積分関数が y'(t)=f(t)=t4 で f(4)(t) が定数である場合のように、両者が等しい場合には(4.17)の剰余項が成立する。そのような場合に限り Simpson の 1/3 則の従来の剰余項は成立するのである。しかし、更に厳密に言えば、2区間の積分はその2区間で確定する被積分関数を使用し、残差関数 F(u) の積分が零になることが確実である一区間毎の積分結果を加算して求めなければならない。従って、剰余項付き Simpson の 1/3 則は以下のように求めなけばならない。
. .
[定理 4.4]. .剰余項付き Simpson の 1/3 則は次のように表される。
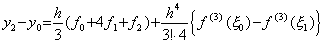 ____(4.23)
[証明]. .(4.12) 及び (4.14)に p=3 を用いると、 ____(4.23)
[証明]. .(4.12) 及び (4.14)に p=3 を用いると、
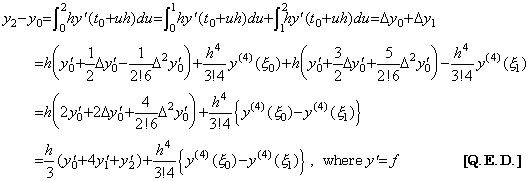
. .
先の例題(4.18)を区分幅 h=1 で t=0 から 1 迄上記証明の区間[0, 1]の積分式で積分する場合には、剰余項及び残差関数 F(u) は次のようになり、F(u) は中点 u=1/2 で零になる。しかし、u=2 では F(u) は零にならない。F(u) が3次関数であり、F(u)=0 となる点は3点だけであるからであるが、この1区間の積分には影響はない。
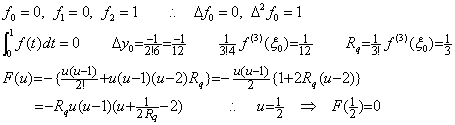 t=1 から 2 迄上記証明の区間[1, 2]の積分式で積分する場合には、剰余項及び残差関数 F(u) は次のようになり、F(u) は u=1 と u=2 の間で零になる。この場合には、u=0 で F(u) は零にならない。この原因は被積分関数が異なる関数を t=1 において f(3)(t) が連続となるように滑らかに接続したものであることにあるが、この1区間の積分には影響はない。
t=1 から 2 迄上記証明の区間[1, 2]の積分式で積分する場合には、剰余項及び残差関数 F(u) は次のようになり、F(u) は u=1 と u=2 の間で零になる。この場合には、u=0 で F(u) は零にならない。この原因は被積分関数が異なる関数を t=1 において f(3)(t) が連続となるように滑らかに接続したものであることにあるが、この1区間の積分には影響はない。
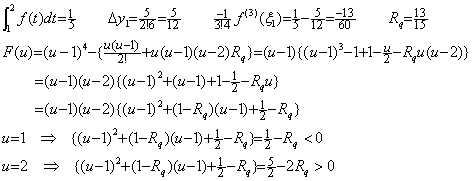 t=0 から 2 迄の積分は両者の和であり、次に示すように定理 4.4 の剰余項が Simpson の 1/3 則の正しい剰余項の値を与える。
t=0 から 2 迄の積分は両者の和であり、次に示すように定理 4.4 の剰余項が Simpson の 1/3 則の正しい剰余項の値を与える。
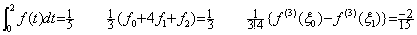 残差関数 F(u) が u=0, 1, 2 の他に各積分区間の中間でも零になるためには、被積分関数 f(t) がこの2区間で同一であり、且つ、 f(3)(t) が更に1回連続微分可能でなければならない。t<1 においても f(t)=(t−1)4 であるならこの条件が満たされ、以下に示すように、区間[0, 1]の積分では u=7/15 で F(u)=0 となり、区間[1, 2]の積分では u=23/15 で F(u)=0 となる。
残差関数 F(u) が u=0, 1, 2 の他に各積分区間の中間でも零になるためには、被積分関数 f(t) がこの2区間で同一であり、且つ、 f(3)(t) が更に1回連続微分可能でなければならない。t<1 においても f(t)=(t−1)4 であるならこの条件が満たされ、以下に示すように、区間[0, 1]の積分では u=7/15 で F(u)=0 となり、区間[1, 2]の積分では u=23/15 で F(u)=0 となる。
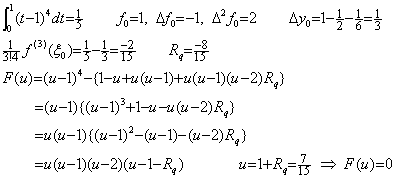
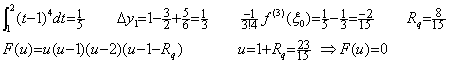 2区間[0, 2]の積分は上記の各区間の積分の和であり、その剰余項の値は次に示すように剰余項なしの Simpson の 1/3 則の値の誤差に一致する。
2区間[0, 2]の積分は上記の各区間の積分の和であり、その剰余項の値は次に示すように剰余項なしの Simpson の 1/3 則の値の誤差に一致する。
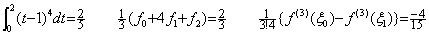 この場合は、f(3)(t) が微分可能であるから、剰余項の差に平均値の定理を適用すれば(4.17)の剰余項に一致する。しかし、これをもって Simpson の 1/3 則が f(4)(ξ) の精度を持つ、即ち、3次関数近似の精度を持つというのは間違いである。
この場合は、f(3)(t) が微分可能であるから、剰余項の差に平均値の定理を適用すれば(4.17)の剰余項に一致する。しかし、これをもって Simpson の 1/3 則が f(4)(ξ) の精度を持つ、即ち、3次関数近似の精度を持つというのは間違いである。
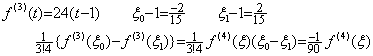 . .
3次関数 f(t) を at3+bt2+ct+d で表すと、 f(3)(t)=3!a であるから t0 から t2 迄の積分は Simpson の 1/3 則で正しく積分できる。しかし、第1項 at3 はこの積分に何の効果も持たない。何故なら、a(t−t0)(t−t1)(t−t2) の t0 から t2 迄の積分は零だからである。更に、この被積分関数に任意の係数 k を持つ関数 k(t−t0)(t−t1)(t−t2) を加えても、積分に何の影響もない。しかし、その関数は f(t) とは甚だしく異なり、1区間の積分、即ち、t0 から t1 迄、及び、t1 から t2 迄の積分は f(t) のそれとは著しく異なる。この原因は3次関数は等間隔区分点を3点用いただけでは不定であることにある。 . .
3次関数 f(t) を at3+bt2+ct+d で表すと、 f(3)(t)=3!a であるから t0 から t2 迄の積分は Simpson の 1/3 則で正しく積分できる。しかし、第1項 at3 はこの積分に何の効果も持たない。何故なら、a(t−t0)(t−t1)(t−t2) の t0 から t2 迄の積分は零だからである。更に、この被積分関数に任意の係数 k を持つ関数 k(t−t0)(t−t1)(t−t2) を加えても、積分に何の影響もない。しかし、その関数は f(t) とは甚だしく異なり、1区間の積分、即ち、t0 から t1 迄、及び、t1 から t2 迄の積分は f(t) のそれとは著しく異なる。この原因は3次関数は等間隔区分点を3点用いただけでは不定であることにある。
. .
任意の関数を3次関数で近似した場合も同じことである。この問題点を解決するためには等間隔点 t3=t2+h を必要とする。この場合、この第3区間の積分は(4.14)の第2式から次のようになる。
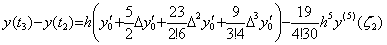 _____(4.24)
従って、(4.21)(4.22)(4.24)により3区間[t0, t3]の積分は次のようになる。 _____(4.24)
従って、(4.21)(4.22)(4.24)により3区間[t0, t3]の積分は次のようになる。
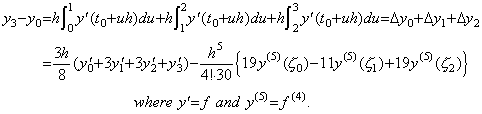 ___(4.25)
. .
これが被積分関数を3次関数で近似した場合の剰余項付き積分公式である。この剰余項は(4.21)と(4.22)の和として得られる Simpson の 1/3 則の剰余項より大きいように見える。しかし、この積分は3区間を積分するのに対して Simpson の 1/3 則はこの場合は被積分関数を3区間を用いて近似し、その2区間を積分しているのであり、この比較は正しくない。比較は Simpson の 1/3 則の等区分間隔を h とすれば 2h/3 の等区分間隔として同じ積分範囲の場合で行わねばならない。 ___(4.25)
. .
これが被積分関数を3次関数で近似した場合の剰余項付き積分公式である。この剰余項は(4.21)と(4.22)の和として得られる Simpson の 1/3 則の剰余項より大きいように見える。しかし、この積分は3区間を積分するのに対して Simpson の 1/3 則はこの場合は被積分関数を3区間を用いて近似し、その2区間を積分しているのであり、この比較は正しくない。比較は Simpson の 1/3 則の等区分間隔を h とすれば 2h/3 の等区分間隔として同じ積分範囲の場合で行わねばならない。
4.4 積分演算子
. .
定理 4.3 と定理 3.7 を比較すると、(4.12) 及び (4.14)に示した積分公式の係数間の関係は(3.33)に示した微分公式の係数間の関係と同じであることがわかる。定理 3.10 の証明は、係数が定理 3.7 に示された関係を満たさねばならないこと以外、実際の値とは無関係なこの性質だけを用いている。従って、(4.12) 及び (4.14)に示した積分公式の逐次階差を求めると、(3.33)の第1式及び定理 3.10 に示した逐次階差の関係と同じ関係がある。
. .
[定理 4.5]. .ak が(4.11)で表されるとし、(4.12) 及び (4.14)の剰余項を AmRem で表すと、0≤m≤p−1 に対して、
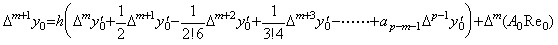 ____(4.26) ____(4.26)
| m=p に対しては、 |
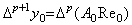 |
(4.27) |
[証明]. .(4.12) 及び (4.14)の各式を一般的に次のように表す。
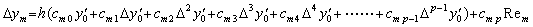 但し、定理 4.3 により、c0k=ak 及び次の関係が存在する。
但し、定理 4.3 により、c0k=ak 及び次の関係が存在する。
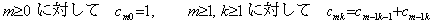 第 m+1 階差 Δm+1y0 は一般的に表された上式の右辺の各項毎の第 m 階差を計算することにより得られる。それは、Am=cmp であるから、剰余項が Δm(A0Re0) と表わされることを除き各項の係数の第 m 階差を計算することになる。
第 m+1 階差 Δm+1y0 は一般的に表された上式の右辺の各項毎の第 m 階差を計算することにより得られる。それは、Am=cmp であるから、剰余項が Δm(A0Re0) と表わされることを除き各項の係数の第 m 階差を計算することになる。
| 1) | . .m=0 なら(4.26)は(4.12)と同じである。 |
| 2) | . .m=1 なら y0' を持つ第1項はその係数が Δc00=c10−c00=1−1=0 であるから、第2階差 Δ2y0=Δy1−Δy0 から消える。k≥1 の各項の係数は Δc0k=c1k−c0k=c0k−1 であるから m=0 の場合の k−1 項の係数になる。故に、
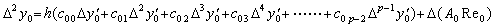 |
| 3) | . .m=2 なら y0' を持つ第1項はその係数が Δ2c00=c20−2c10+c00=1−2+1=0 であるから、第3階差 Δ3y0=Δy2−2Δy1+Δy0 から消える。Δy0' を持つ第2項も係数が次のようになるから消える。
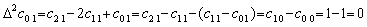
k≥2 の各項の係数は次に示すように m=1 の場合の k−1 項の係数になる。
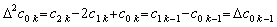 故に、. .
故に、. .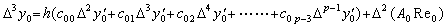 |
| 4) | . .m=n のとき(4.26)が成立すると仮定すると、Δn−1y0' 迄の項の係数は零になる。故に、
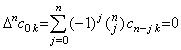 . .(k<n),______ . .(k<n),______
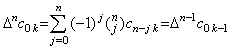 . .(k≥n), . .(k≥n),
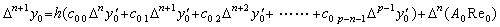 従って、m=n+1 のとき、
従って、m=n+1 のとき、
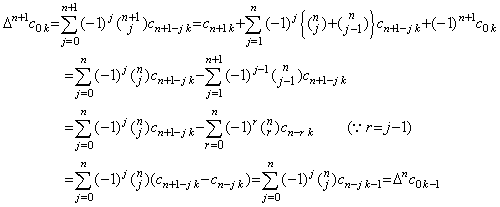 但し、仮定により k−1<n のとき Δnc0k−1=0 であるから、k≤n のとき Δn+1c0k=0 である。故に、
但し、仮定により k−1<n のとき Δnc0k−1=0 であるから、k≤n のとき Δn+1c0k=0 である。故に、
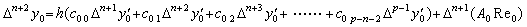 |
| 5) | . .上記の場合、整数 k は 0≤k≤p−1 でなければならない。故に、n+1=p なら係数の添え字が p−n−2<0 となるので剰余項以外の全ての項は消えるから、上式は Δp+1y0=Δp(A0Re0) になる。 |
| [Q.E.D.] |
. .
定理 4.5 により、(4.8)に示した導関数 y' (t) の積分は次の行列演算式で表される。要素 Δp+1y0 は被積分ベクトル Y0' に無関係で、剰余項の要素 Δp(A0Re0) のみに関係するから左辺に記述しなくてよい。
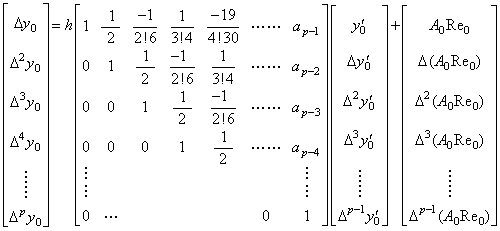 ___(4.28) ___(4.28)
. .
[定理 4.6]. .整数 k が 0≤k≤p のとき、
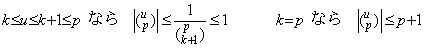 ____(4.29)
[証明]. .0≤k≤p−1 なら次の関係がある。 ____(4.29)
[証明]. .0≤k≤p−1 なら次の関係がある。
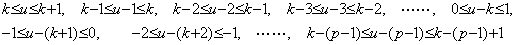 従って、j≤k なら |u−j| の最大値は上限であり、j≥k+1 なら下限の絶対値である。故に、
従って、j≤k なら |u−j| の最大値は上限であり、j≥k+1 なら下限の絶対値である。故に、
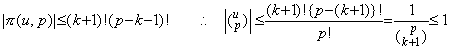 k=p なら (u−j) の最後の値は 1≤u−p+1≤2 であり全てが正であるから、
k=p なら (u−j) の最後の値は 1≤u−p+1≤2 であり全てが正であるから、
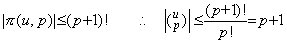 ______[Q.E.D.] ______[Q.E.D.]
. .
定理 4.6 により、
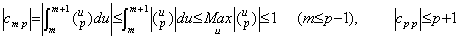 ___(4.30). .
(4.28)の剰余項は u=m に対してそれぞれ次に示す Am 及び Rem の値を持つ二つの関数の積のベクトルである。 ___(4.30). .
(4.28)の剰余項は u=m に対してそれぞれ次に示す Am 及び Rem の値を持つ二つの関数の積のベクトルである。
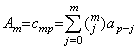 _________ _________
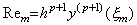 故に、それぞれの関数のベクトルである二つのベクトルの積で表せる。関数値 Am の逐次階差は明らかに ap−m である。従って、二つのベクトルは次のようになる。
故に、それぞれの関数のベクトルである二つのベクトルの積で表せる。関数値 Am の逐次階差は明らかに ap−m である。従って、二つのベクトルは次のようになる。
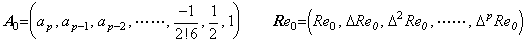 剰余項は R0=A0×Re0 で表される。但し、(4.28)では両ベクトルの最後の要素は省略されている。ベクトル A0 が展開される行列の主対角要素は cmp であり、ベクトル Re0 のそれは Rem であるから、(4.30)により、
剰余項は R0=A0×Re0 で表される。但し、(4.28)では両ベクトルの最後の要素は省略されている。ベクトル A0 が展開される行列の主対角要素は cmp であり、ベクトル Re0 のそれは Rem であるから、(4.30)により、
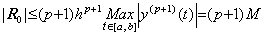 被積分関数 y' (t) がベクトル Y0' で表せるとき条件 M=0 or h→0 が存在するので、条件 R0→0 及び Δp+1y0→0 は満たされる。故に、(4.28)の行列を D−1 で表すと、この行列演算式は次のように表される。
被積分関数 y' (t) がベクトル Y0' で表せるとき条件 M=0 or h→0 が存在するので、条件 R0→0 及び Δp+1y0→0 は満たされる。故に、(4.28)の行列を D−1 で表すと、この行列演算式は次のように表される。
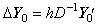 ________(4.31)
. .
左辺 ΔY0 は差 Y1−Y0 に等しい、即ち、 Δy(t)=y(t+h)−y(t) をベクトルで表す。従って、(4.28) 及び (4.31)は次のように(4.1)に示した積分の差をベクトルで表す。演算子 hD−1 は被積分関数 y' (t) の任意の点 t からの区間 h の積分を意味する。 ________(4.31)
. .
左辺 ΔY0 は差 Y1−Y0 に等しい、即ち、 Δy(t)=y(t+h)−y(t) をベクトルで表す。従って、(4.28) 及び (4.31)は次のように(4.1)に示した積分の差をベクトルで表す。演算子 hD−1 は被積分関数 y' (t) の任意の点 t からの区間 h の積分を意味する。
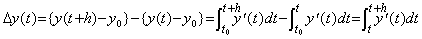 _____(4.32)
(Δ+1)y(t)=y(t+h) であるから、 _____(4.32)
(Δ+1)y(t)=y(t+h) であるから、
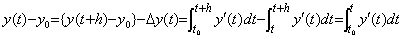 _____(4.33)
この式は(4.1)と同じであり、右辺の積分演算子は(4.32)とは異なるから、行列演算式(4.31)は通常の積分演算(4.1)とは少し異なる。しかしその違いは僅かであり、左辺の Δy(t) と y(t)−y0 のベクトルの違いから簡単に(4.1)の積分演算の行列演算式を導くことができる。Δy(t) のベクトルは(4.28)に示したように第1要素が Δy0 であるが、y(t)−y0 のベクトルの第1要素は零であり、第2要素以降は Δy(t) のベクトルの要素を1要素下にずらしたものである。第2節において、演算子 ΔT がこの演算を行う演算子であることを述べた。この演算子は行列に左より掛けると、各行を1行下にずらし、第1行に零を詰める。従って、(4.31)の両辺に演算子 ΔT を左より掛ければ積分演算(4.1)に相当する行列演算式(4.34)を得る。従って、厳密な意味の積分演算子は hΔTD−1 であるが、第1要素は計算で得るものではなく、通常、計算は(4.31)で行うので hD−1 を積分演算子と呼ぶ。これは積分定数を規定しない不定積分と考えることができる。 _____(4.33)
この式は(4.1)と同じであり、右辺の積分演算子は(4.32)とは異なるから、行列演算式(4.31)は通常の積分演算(4.1)とは少し異なる。しかしその違いは僅かであり、左辺の Δy(t) と y(t)−y0 のベクトルの違いから簡単に(4.1)の積分演算の行列演算式を導くことができる。Δy(t) のベクトルは(4.28)に示したように第1要素が Δy0 であるが、y(t)−y0 のベクトルの第1要素は零であり、第2要素以降は Δy(t) のベクトルの要素を1要素下にずらしたものである。第2節において、演算子 ΔT がこの演算を行う演算子であることを述べた。この演算子は行列に左より掛けると、各行を1行下にずらし、第1行に零を詰める。従って、(4.31)の両辺に演算子 ΔT を左より掛ければ積分演算(4.1)に相当する行列演算式(4.34)を得る。従って、厳密な意味の積分演算子は hΔTD−1 であるが、第1要素は計算で得るものではなく、通常、計算は(4.31)で行うので hD−1 を積分演算子と呼ぶ。これは積分定数を規定しない不定積分と考えることができる。
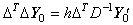 _______(4.34). .
初期値 y0 が与えられているとき、ベクトル y01 を加えれば関数 y(t) を表すベクトル Y0 を得る。この初期値 y0 が導関数 y'(t) を計算する前の初期値 y(t0) であることを明確に示すには、初期値ベクトル抽出演算子 U0 とベクトル Y0 の積で表すことができ、ベクトル Y0 を求める式は次のように表される。初期値ベクトル抽出演算子 U0 は第1行1列の要素のみが1である行列単位である。 _______(4.34). .
初期値 y0 が与えられているとき、ベクトル y01 を加えれば関数 y(t) を表すベクトル Y0 を得る。この初期値 y0 が導関数 y'(t) を計算する前の初期値 y(t0) であることを明確に示すには、初期値ベクトル抽出演算子 U0 とベクトル Y0 の積で表すことができ、ベクトル Y0 を求める式は次のように表される。初期値ベクトル抽出演算子 U0 は第1行1列の要素のみが1である行列単位である。
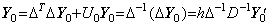 ________(4.35)
この式は微分方程式の解を求める公式である。微分演算公式(3.40)を(4.35)に代入すると、 ________(4.35)
この式は微分方程式の解を求める公式である。微分演算公式(3.40)を(4.35)に代入すると、
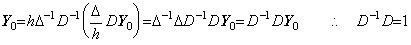 ______(4.36)
故に、著者は h(ΔD)−1 を微分演算子 Δh−1D の逆演算子と定義する。(4.36)は以下に示すように両行列が同じ次数なら剰余項が零に漸近することとは無関係に成立する。 ______(4.36)
故に、著者は h(ΔD)−1 を微分演算子 Δh−1D の逆演算子と定義する。(4.36)は以下に示すように両行列が同じ次数なら剰余項が零に漸近することとは無関係に成立する。
. .
[定理 4.7]. .D−1D=1 は任意の次数の行列について成立する。
[証明]. .1). .行列の次数が一次のときは明らかに成立する。
| 2) | . .行列が2次なら、
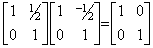 |
| 3) | . .行列が n 次のとき成立すると仮定すると、行列が n+1 のときも以下に示すように成立する。行列 D−1 及び D の第1行の要素をそれぞれ ak 及び dk で表すと、示すべきは次式の証明である。
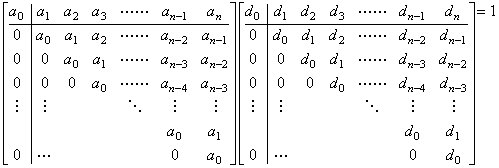 . .
左の行列の第 i 行を Ai で表し、右の行列の第 j 列を Dj で表す。i≥2 の場合には Ai の第1要素が全て零であるから、Ai と D1 の積は全て零になる。j≥2 の場合の Ai と Dj の積は2本の線で分けられた n 次の小行列の積になる。その積は仮定により単位行列の小行列になる。i=1 のとき、第1行 A1 と第 j 行 Dj の積は j=1 なら1であるが、2≤j≤n なら全て零になる。何故なら、Dj の最後の要素は j≤n のとき、即ち、最後の行以外は零であり、その積は左の n 次の小行列の第1行と右の n 次の小行列の積に同じであるからである。故に、第1行 A1 と最後の行 Dn+1 の積が零になることを示せば証明は完了する。その積を s で表せば次のようになる。 . .
左の行列の第 i 行を Ai で表し、右の行列の第 j 列を Dj で表す。i≥2 の場合には Ai の第1要素が全て零であるから、Ai と D1 の積は全て零になる。j≥2 の場合の Ai と Dj の積は2本の線で分けられた n 次の小行列の積になる。その積は仮定により単位行列の小行列になる。i=1 のとき、第1行 A1 と第 j 行 Dj の積は j=1 なら1であるが、2≤j≤n なら全て零になる。何故なら、Dj の最後の要素は j≤n のとき、即ち、最後の行以外は零であり、その積は左の n 次の小行列の第1行と右の n 次の小行列の積に同じであるからである。故に、第1行 A1 と最後の行 Dn+1 の積が零になることを示せば証明は完了する。その積を s で表せば次のようになる。
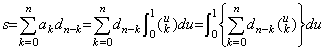 ______(4.37). .
次のような関数 f(u) を考える。 ______(4.37). .
次のような関数 f(u) を考える。
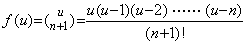 この関数は p=n+1 の剰余項付き Newton の補間公式で表すことができる。但し、f(n+2)(u)≡0 であるから剰余項は零である。等間隔 h=1 の区分点を u=0, 1, 2, ………, n+1 とすると、f0=f1=f2= ………=fn=0 及び fn+1=1 であるから、逐次階差は k≤n のとき Δkf0=0 であり、Δn+1f0=1 である。従って、この補間公式は又 f(u) と表せる。Newton の補間公式の導関数は f(n+2)(u)≡0 の場合は任意の点で剰余項は零である。(3.29)により、
この関数は p=n+1 の剰余項付き Newton の補間公式で表すことができる。但し、f(n+2)(u)≡0 であるから剰余項は零である。等間隔 h=1 の区分点を u=0, 1, 2, ………, n+1 とすると、f0=f1=f2= ………=fn=0 及び fn+1=1 であるから、逐次階差は k≤n のとき Δkf0=0 であり、Δn+1f0=1 である。従って、この補間公式は又 f(u) と表せる。Newton の補間公式の導関数は f(n+2)(u)≡0 の場合は任意の点で剰余項は零である。(3.29)により、
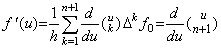 著者の演算子法はこの導関数を剰余項付きの行列演算式で表す。但し、剰余項は恒等的に零である。故に、
著者の演算子法はこの導関数を剰余項付きの行列演算式で表す。但し、剰余項は恒等的に零である。故に、
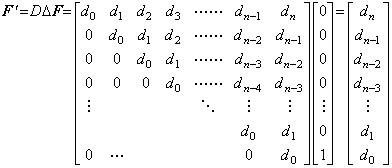 従って、導関数 f ' (u) はベクトル F' の要素を用いて Newton の補間公式で表せる。それは(4.37)の被積分関数になる。故にその積分は次のようになる。
従って、導関数 f ' (u) はベクトル F' の要素を用いて Newton の補間公式で表せる。それは(4.37)の被積分関数になる。故にその積分は次のようになる。
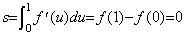 ________[Q.E.D.] ________[Q.E.D.] |
. .
(4.35)の積分演算子は演算子 Δ の逆演算子 Δ−1 を持つ。しかし、行列 Δ は det(Δ)=0 であり、逆行列は存在しないから逆行列ではない。それは第 2.4 節において行列演算式 Δ−1Δ=ΔTΔ+U0=1 で定義された。従って、この積分演算子は(4.31)により ΔY0 を求めた後、初期値 y0 をこの式により演算しなければならない。
. .
[定理 4.8]. .k≥0 のとき、行列 D 及び D−1 の第1行 k+1 列の要素をそれぞれ dk 及び dk−1 で表すと、
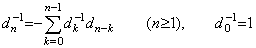 ______(4.38)
[証明]. .(4.37)の s の値は n≥1 のとき零であるから、 ______(4.38)
[証明]. .(4.37)の s の値は n≥1 のとき零であるから、
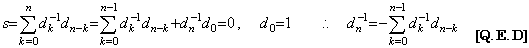
. .
行列 D の第1行 k+1 列の要素は k≥0 に対して (−1)k/(k+1) により容易に得られる。従って、行列 D−1 の第1行 n+1 列の要素は Stirling 数を使わなくても定理 4.8 により n≥0 に対して逐次に得られる。
次 4.5 予測子と修正子 へ
|
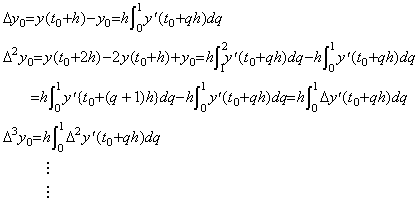
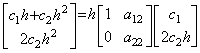
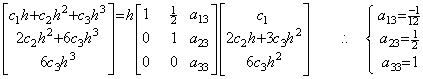
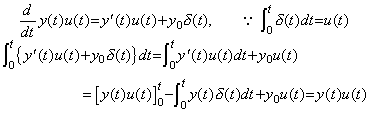
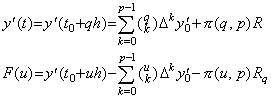
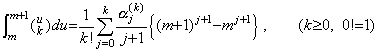 ____(4.10)
____(4.10)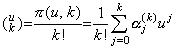 ______且つ______
______且つ______
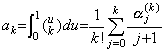 ______(4.11)
______(4.11)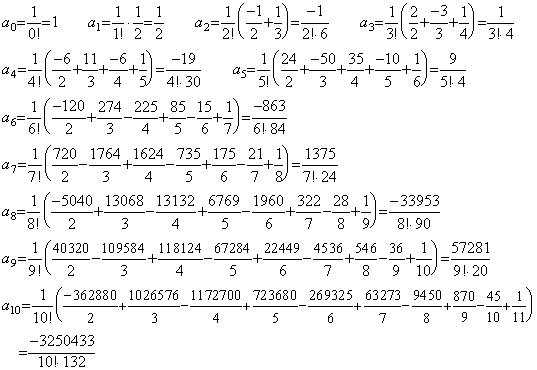
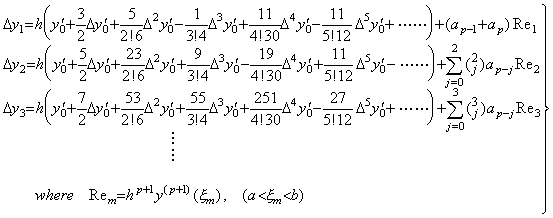 (4.14)
(4.14)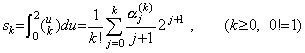
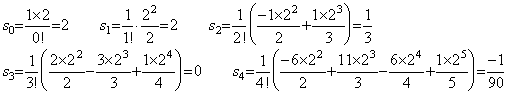
 . .
残差 F(u) は u=q において零になり、|u−q| の増加と共にその絶対値を増加する。何故なら、定数 Rq と任意の u に対する R の真の値との差は増加するからである。しかし、それは
. .
残差 F(u) は u=q において零になり、|u−q| の増加と共にその絶対値を増加する。何故なら、定数 Rq と任意の u に対する R の真の値との差は増加するからである。しかし、それは 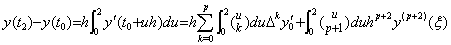 ____(4.19)
____(4.19)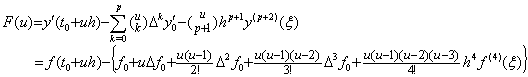 ___(4.20)
___(4.20)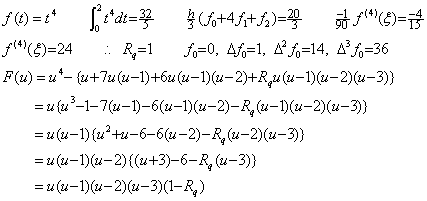
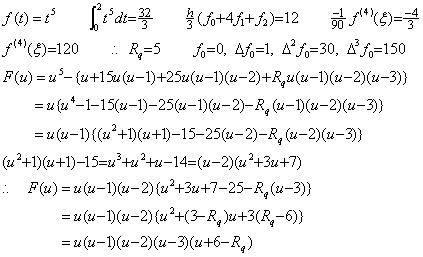
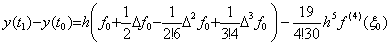 ____(4.21)
____(4.21)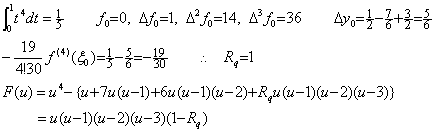 ____
____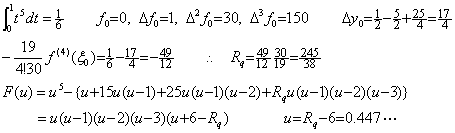 ____
____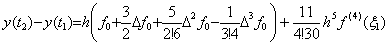 ____(4.22)
____(4.22)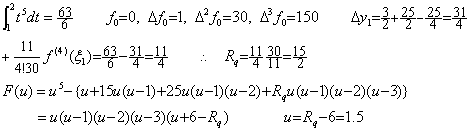
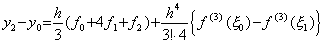 ____(4.23)
____(4.23)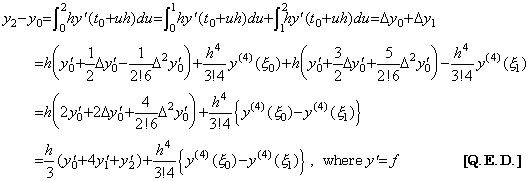
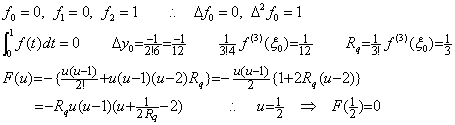
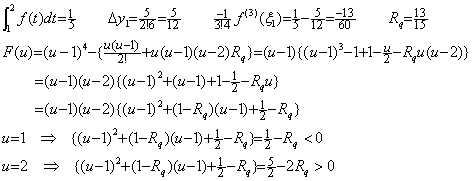
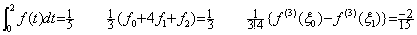
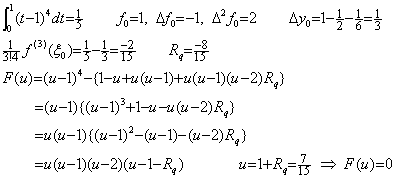
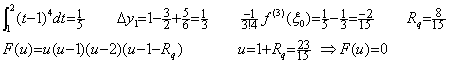
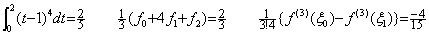
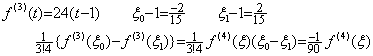
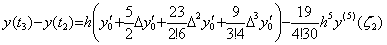 _____(4.24)
_____(4.24)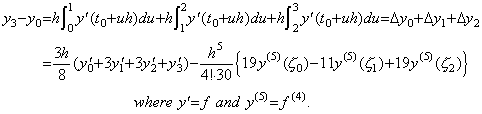 ___(4.25)
___(4.25)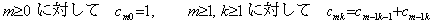
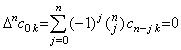 . .(k<n),______
. .(k<n),______
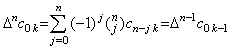 . .(k≥n),
. .(k≥n),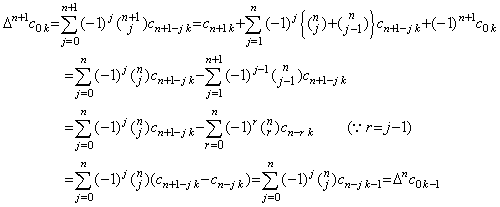
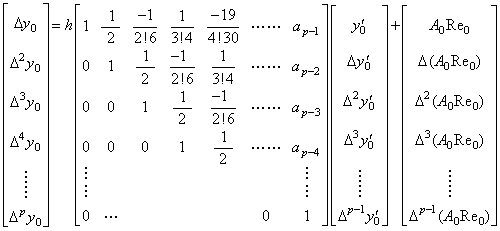 ___(4.28)
___(4.28)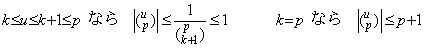 ____(4.29)
____(4.29)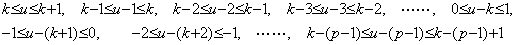
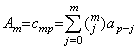 _________
_________
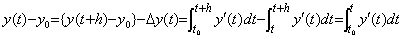 _____(4.33)
_____(4.33)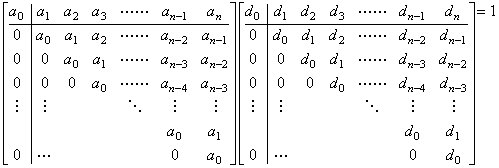
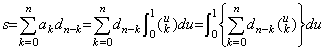 ______(4.37)
______(4.37)