2. 演算子
2.1 ベクトルで表せない商
. .
ベクトル W が二つのベクトル Y と Z の積であるとき、商 W/Z はベクトル Y である。しかし、任意の二つのベクトルの商であるベクトルが常に存在するとは限らない。行列 A が任意の正方行列のとき W=AZ を満たすベクトル W が存在する。しかし、それはベクトル W 及び Z をそれぞれ展開した行列 W, Z について W=AZ を常に成立させるとは限らない。何故なら、積 AZ は常に三角行列とは限らないからである。もし、三角行列であったとしても、第 1.4 節で述べたベクトルの展開であるための条件を常に満たすとは限らない。故に、商の概念は更にこれらの行列に拡張しなければならない。それは整数系の有理数系への拡張に類似である。
. .
著者は、正方行列 A 及びベクトル Z が等式 W=AZ を満たすとき、行列 A を演算子と呼ぶ。W=0 なら det(A)=0 か Z=0 であるが、Z=0 なら行列 A は不定であり商ではない。Z≠0 なら det(A)=0 であるが、A=0 なら行列 A は商であり、A≠0 なら 2A, 3A, ………でも W=0 が成立するから不定であり商ではない。但し、行列 A がベクトルの行列展開の場合は前節のベクトルの商の拡張である。これらの商でない演算子はベクトル 0 とベクトル Z の関係から求めることは出来ないのであり、これらの行列の零でない要素は全て予め与えられていなければならない。又、商の形式に表記することは出来ない。微分方程式の解が初期値を与えられることにより一意となるように、これらの演算子はその零でない要素全ての値が与えられた値であることにより一意である。行列 A が商であり、W=AZ であるとき、0=BZ を満たす零でない行列 B が存在するなら、W=(A+B)Z が成立する。このとき、
. . [定義]. .任意のベクトル W と Z≠0 が正方行列 A により W=AZ で表され、W=0 なら A=0 であるとき、行列 A を商と定義する。但し、0=BZ となる零でない行列 B が存在するなら、行列 B の零でない要素と同じ位置にある A の要素は値が全て既知でなければならない。
. .
[定理 2.1]. .ベクトルの形式を持たない商は一意である。
[証明]. .
行列 A 及び B はベクトルの形式を持たない商であり、Z≠0 に対して W =AZ 且つ、W =BZ であると仮定すると、(2.1)が満たされねばならない。
. .
下に示すように、ベクトル Z に対して同じ結果を与える行列 A と B がある。行列 (A−B) は第2列以外の要素は全て零であるから、行列 (A−B) は零でないけれども (A−B)Z は零である。ベクトル Z の第2要素は零であるから行列 A, B の第2列の要素は任意の値でよい。
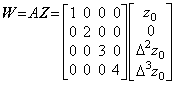 _____
_____
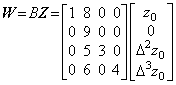 ______(2.2)
______(2.2) . . 等式 W=AZ において A≠0 且つ det(A)=0 のとき二つの場合がある。行列 A がベクトルの行列展開であるとき 1.6 節で述べた拡張された商であり、ベクトルの形式を持たないとき演算子であるが商ではない。このとき、Z≠0 に対して 0=BZ となる det(B)=0 の行列 B が存在するなら、W=(A+B)Z となり、演算子は一意でないことになるが、この場合も行列 B の零でない要素と同じ位置にある A の要素は値が全て既知でなければならないという条件をつけることにより行列 (A+B) は W=AZ を満たす演算子ではなく、演算子は一意となる。
. . 等式 W=AZ において det(A)≠0 のとき、逆行列が一意に存在して Z=A−1W であるが、det(A)=0 の場合は逆行列は存在しない。しかし、行列 A が演算子の場合は行列式を使用しないで逆演算子を定義することが出来る。例として、(2.2)の第1式の演算子 A の第4行4列の値が零の場合を(2.2a)に示す。第2式の逆演算子 B の第4行4列の値は 1/0=∞ であり、逆演算により元のベクトル Z に戻るためには Δ3z0 は与えられていなければならない。従って、この値が右辺の影響を受けないために逆演算子 B の第4行4列の値は零とする。両演算子の積 BA は単位行列の第4行4列の値を零にしたものとなる。この逆演算子 B も恒等演算子 BA も予め与えられているべき要素 Δ3z0 の演算は行わないことを前提としている。しかし、演算を数式通り行うと Δ3z0 の値は零となるので、与えられた要素の値を加算する演算を必要とし、通常の逆演算子や恒等演算子はこの加算演算を含めたものを指し、合成演算子である。本演算子法では前者の意味の逆演算子も使用し、逆演算子は下記[定義]に示すように定義できる。
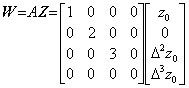 _____
_____
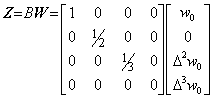 ______(2.2a)
______(2.2a). . [定義]. .任意の演算子の逆演算子は両者の積が対角行列となり、その対角要素が全て1となるか、又は、その幾つかは零となる行列である。但し、零である対角要素に対応する左辺のベクトルの要素は予め与えられていなければならない。
. . この逆演算子を求めるには、逆演算子 B の全要素を未知数として演算子 A との積 BA が単位行列となるように連立方程式を構成し、解けばよい。その際、不定又は不能となる要素の値は零とする。(2.2a)の例でこれを示すと、変数の数は16個で方程式の数も16個であるから解は定まる。B の第1行と A の第1列の積から b11=1、B の第2行と A の第2列の積から b22=1/2、B の第3行と A の第3列の積から b33=1/3、B の第4行と A の第4列の積から b44×0=1 となるが不能であるから b44=0、その他の要素は全て零となる。従って、(2.2a)の第2式の行列 B が得られる。この逆演算において Δ3z0 はベクトル W に変換される前のベクトル Z の Δ3z0 が与えられていなければならない。
. .
[定理 2.2]. .逆演算子は一意である。
[証明]. .
W=AZ である演算子 A の逆演算子が2つあるとし、それらを B と C で表すと、Z=BW 且つ Z=CW であるから、0=(B−C)W 且つ、det(B−C)=0 である。B−C≠0 ならその零でない要素に対応するBとCの要素の値は共に同じ値が与えられていなければならない。これは B−C≠0 と矛盾する。故に、B−C=0 である。__[証明終]
. .
第1列の要素が全て零である演算子が存在する。従来の写像という概念では初期値が写像されないから逆演算結果は初期値が不定であり、逆演算は一意でないという。この場合、写像により初期値が失われると考えている。本演算子法では初期値は原空間に残され、逆写像は原空間への写像であるからそれが使われると考える。これが、初期値が既知でなければならないとか、与えられていなければならない、又は、元に戻すという意味であり、原空間には初期値等の必要なものは常に存在するが、原像からは除外されると考える。通常、微分演算は(2.2c)の第1式で定義される。しかし、厳密な定義は(2.2c)の第2式でなければならず、微分演算子の被演算関数は y(t)−y0 である。従って、微分演算結果が恒等的に零なら被演算関数が恒等的に零であるということが成立する。
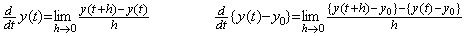 ____(2.2c)
____(2.2c) ________(2.2d)
________(2.2d)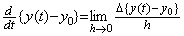
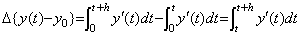
2.2 演算子系
. .
著者はベクトル W 及び Z が任意の行列 A により W=AZ と表されるとき、行列 A を演算子と呼ぶ。演算子は以下に示すように四則演算が成立する。
. .[定理 2.3]. .演算子の和および差は演算子である。
[証明]. .演算子 A, B 及び任意のベクトル Z に対して W=AZ 及び Y=BZ であると仮定すると、
. . [定理 2.4]. .演算子の積は演算子である。
[証明]. .演算子 A, B 及び任意のベクトル Z に対して W=AY 及び Y=BZ であると仮定すると、
. . 演算子の和、差、積は同じ次数の正方行列の演算である。従って、演算子は明らかに以下の行列の性質を保持する。
| A. | . .任意の演算子 A, B, C に対して、 | |
| (A1). .A+B=B+A | (A2). .(A+B)+C=A+(B+C) | |
| (A3). .A+0=A となる演算子 0 が存在する。 | ||
| (A4). .任意の演算子 A に対して、A+(−A)=0 となる演算子 −A が存在する。 | ||
| B. | . .任意の演算子 A, B, C に対して、 | |
| (B1). .(AB)T=BTAT | (B2). .(AB)C=A(BC) | |
| (B3). .A(B+C)=AB+AC | (B4). .(B+C)A=BA+CA | |
| C. | . .任意の演算子 A, B 及びスカラー α, β に対して、 | |
| (C1). .1•A=A | (C2). .α(βA)=(αβ)A | |
| (C3). .(α+β)A=αA+βA | (C4). .α(A+B)=αA+αB | |
. . [定理 2.5]. .演算子の商は演算子である。
[証明]. .任意の演算子 C, B(≠0) 及びベクトル Z≠0 に対して W=CZ 及び Y=BZ と仮定する。行列 A が存在して C=AB が成立するとき、演算子 C の第 i 行ベクトルと行列 A の第 i 行ベクトルの関係は Ci=AiB と表され、Ai は連立方程式の解である。
det(B)=0 のとき、解 Ai は不定であり、行列 A は不定であるから商ではない。
det(B)≠0 のとき、解 Ai は一意に定まり、行列 A は一意であるから商である。仮定により、
. . 上記のように、演算子の四則演算が存在するから独立変数が演算子である演算子値関数を定義することができる。それについては後で述べる。以下に述べる定理によりベクトル値関数はベクトルを行列展開すれば演算子値関数でもある。
. .[定理 2.6]. .ベクトルは演算子である。
[証明]. .任意のベクトル Y は行列 Y に展開でき、
_______Y=Y1=Y1_______[証明終]
. .
[定理 2.7]. .ベクトルの商は演算子である。
[証明]. .ベクトルの商 W/Z はベクトル Y の行列展開 Y 又はその他の行列 A により、
. . ベクトルは演算子であるけれども、積の交換則は常に成立する。その他の演算子は交換則が常には成立せず、通常、積の転置による順序入れ替えの規則を必要とすることに注意が必要である。ベクトルと演算子の積が連続しているとき、行列の積として矛盾する結果になる交換又は結合操作は認められない。例えば、演算子 A 及びベクトル Y, Z の積(2.3)は積 AZ がベクトルであるから正しい。しかし、右辺を更に A(ZY) 又は A(YZ) と変えるのは常には認められない。何故なら、それはベクトル Y と行列 A の積に正しくない交換操作をしたのと同じ結果になるからである。
| Y(AZ)=(AZ)Y | (2.3) |
. . ベクトルである演算子のノルムはベクトルのノルムである。他の演算子のノルムを最大値として定義するのは簡単ではない。しかし、数値計算において通常使われる演算子は次節で述べるように簡単な性質を持ち、ノルムは容易に定義できる。それについては後で述べる。
. . ここで、演算子が四則演算により結合することの出来る量の最上位概念である系が考えられる。それは次のように構成される。
. . 通常の演算子法においても演算子は数、関数及び数学的演算子からなる系の最上位概念である。従って、それらの間で四則演算をすることが出来なければならない。Mikusinski は関数の積分を演算子と関数の積で表すために積の概念を畳込み積分へ拡張し、演算子を商として定義した。ラプラス変換はその拡張を明示的には使用しないで、実数変数 t の関数 f(t) を実数又は複素数の補助変数 s の関数 F(s) に変換することにより目的を達成している。
. . 著者の演算子法は積の概念を拡張することなく、演算子を行列に変換し、関数と数をベクトルに変換することにより、関数に対する演算を演算子と関数の積で表すことが出来る。従って、四則演算は行列とベクトルの四則演算となる。但し、2つのベクトルの積を実行するときは、被乗数ベクトルは行列に展開される。
2.3 階差演算子
. .
第 1.3 節で定義したベクトルの階差 ΔY0=Y1−Y0 は(2.5)に示す行列とベクトルの積で表すことが出来る。ベクトル Y0 は y0 から yp 迄の階差で定義され、ベクトル Y1 は y1 から yp+1 迄の階差で定義されるので、ベクトル ΔY0 は y0 から yp+1 迄の階差で定義される。この範囲では、ベクトル Y0 は y0 から Δp+1y0 迄の要素で構成される。即ち、p+2 次元空間に存在する。(2.5)の最右辺は、ベクトル ΔY0 は Δy0 から Δp+1y0 迄の要素で構成される p+1 次元部分空間への Y0 の射影であることを示す。
. .
一方、第1右辺 Y1−Y0 のベクトル Y0 は y0 から Δpy0 で構成される p+1 次元部分空間への最右辺のベクトル Y0 の射影である。射影は要素 Δp+1y0の切り捨てであるから混乱の恐れがなければこの両ベクトルに同じ表記を用いてよい。この切り捨てられる要素は p+1 次元部分空間のベクトル Y0 に対しては無視できるが、ベクトル ΔY0 に対しては必ずしも無視できない。従って、ベクトル ΔY0 はその要素を持ち、要素 Δp+2y0 は行列とベクトルの積により零であるから省略される。それは、適当な精度において要素 Δp+1y1 は要素 Δp+1y0 に等しいことを示す。
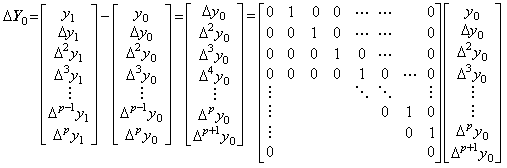 . .(2.5)
. .(2.5). . 上式の行列は主対角要素の次の要素にのみ値1を持ち、他の要素には零を持つ正方行列である。ベクトル Y0 の前の記号 Δ はこの行列を表し、ベクトルの要素に使われる記号 Δ は単に2つの数値の差を表すから、これとは異なる。しかし、行列演算式の結果は、記号 Δ をスカラーと考えれば Δ と Y0 の積に等価である。従って、両者を区別する必要はないので同じ記号で表す。
. . ベクトルを Y0=(c, 0, 0, ……)と仮定すると、行列 Δ とベクトル Y0 の積は行列 Δ は零でないのに ΔY0=0 になる。従って、行列 Δ はベクトル 0 の Y0 による商ではなく、第 2.2 節で述べた演算子である。ベクトル Y0 を行列 Y0 に展開すると、行列 Δ と行列 Y0 の積は(2.6)に示すように零ではない。従って、演算子 Δ は左辺の演算子の演算子 Y0 による商である。これらは 0.1 と 3 の積は整数では零であるが、実数では 0.3 である関係に類似である。著者は行列 Δ を階差演算子と定義する。
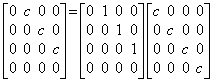 _____(2.6)
_____(2.6). . 行列 A が三角行列で、上の行と同じ要素を持ち、各要素が1要素右にシフトされ、第1要素に零が与えられた行で構成されているなら、演算子 Δ と行列 A の積は交換可能、即ち、(2.7)に示すように ΔA=AΔ である。
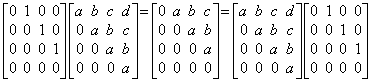 ____(2.7)
____(2.7)2.4 和分演算子
. .
差分演算子 Δ は行列式が det(Δ)=0 であるから逆行列を持たない。しかし、初期値 y0 が逆演算において保持されるなら、 Δ と Y0 の積から Y0 を回復する逆演算子は存在する。それを Δ−1 と表すと、逆演算子は(2.8)で定義され、和分演算子と呼ばれる。この逆演算子は加算演算子を含んでいる。差分演算子は通常 Δy(t)=y(t+h)−y(t) で定義されるが、厳密な定義は Δ{y(t)−y0}={y(t+h)−y0}−{y(t)−y0} である。従って、逆演算は y(t)−y0 を得る。本演算子法でも同様に、差分演算子の被演算子は厳密には Y0−y01 であり、逆演算子は第 2.1 節の逆演算子の定義により転置行列 ΔT である。しかし、混乱は生じないので通常の定義における差分演算子の逆演算子を Δ−1 で表す。
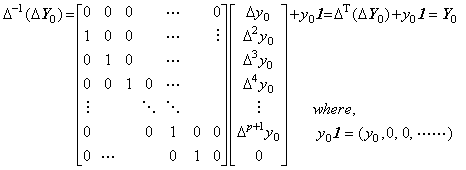 ___(2.8)
___(2.8)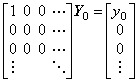 ____(2.9)_______
____(2.9)_______
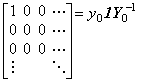 ____(2.10)
____(2.10)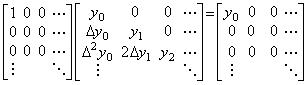 _____(2.11)
_____(2.11). . [定理 2.8]________ ΔΔ−1=Δ−1Δ=1.
[証明]. .(2.8)において、y01 を U0Y0 で置き換えると、
| 故に、 | ΔΔ−1=ΔΔT=1 | [証明終] |
. . 通常の理論では、階差演算子に逆演算子を右より掛けると恒等演算子になるが、左より掛けると恒等演算子にならない。(2.8)に示すように、演算子 ΔT がこの通常の逆演算子に相当する。しかし、演算子 ΔT は積 ΔTΔ が(2.13)に示すように恒等演算子でないから本演算子法では階差演算子の逆演算子 Δ−1 として表さない。この演算子は第 2.1 節で述べたように初期値が与えられていて、その計算をしないことを必要とする逆演算子であり、その初期値を加算することを含む逆演算を1つの記号で表したものが Δ−1 である。しかし、被演算関数が y(t)−y0 である場合は両者の区別は必要なくなる。
. . 演算子 ΔT はそれに続く行列の各行を1行下にシフトし、結果の行列を正方行列で表すために最後の行を省略する。そして、第1行を零で埋める。しかし、演算子 Δ−1 は前もって与えられた第1行を回復する。その関係は(2.13)の各辺に任意の行列 M を右より掛けた(2.14)に表される。
2.5 シフト演算子
. .
著者はベクトル Y0 に対してベクトル Y1 を与える演算子をシフト演算子と定義し、記号 E で表す。この演算子は階差演算子と(2.15)の関係にある。
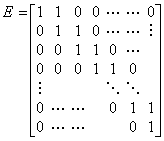 ________
________
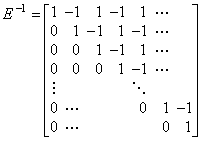
. . [定理 2.9]________Y0=E−1Y1
[証明]. .
1). .E−1Y1 の最後の要素は Δp+1y1 である。それは Y1=EY0 の最後の要素であるから Δp+1y0 に等しい。
2). .E−1Y1 の p+1 番目の要素は、

. . 行列 E−1 はベクトル Y1 に対してベクトル Y0 を与える演算子であるから逆シフト演算子である。
2.6 演算子値関数
. .
著者は演算子値変数 X に対して演算子 Y を与える関数を演算子値関数と定義し、それを Y=F(X) で表す。ベクトル値関数 F(X) はベクトルが行列に展開されれば演算子値関数である。例えば、ベクトル値関数
. .
シフト演算子 E は一次関数 Y=X+1 の X=Δ に対する演算子値であり、逆シフト演算子 E−1 は関数 Y=(X+1)−1 の X=Δ に対する演算子値である。逆に、階差演算子 Δ は逆関数 X=Y−1 の Y=E に対する演算子値であり、和分演算子 Δ−1 は関数 X=(Y−1)−1 の Y=E に対する演算子値である。和分演算子は又、(2.13)により陰関数 YX=ΔTX+U0 又は YX=1 の X=Δ に対する演算子値である。
. .
演算子 Δ2 は関数 Y=X2 の X=Δ に対する演算子値であり、積 Δ×Δ により得られる。それは、左の演算子 Δ が右の演算子 Δ の各行を1行上へシフトするから、(2.16)に示すように、主対角要素の二つ右隣の要素が値 1 であり、他の全ての要素の値が零である行列になる。一般に、演算子 Δp は p 乗関数 Y=Xp の X=Δ に対する演算子値であり、主対角要素の p 個右隣の要素が値 1 であり、他の要素は全て零である行列である。
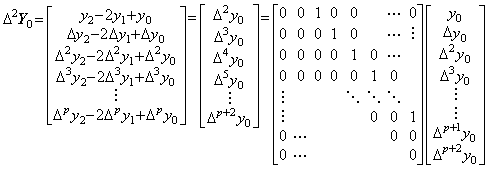 ___(2.16)
___(2.16). .
[定理 2.10]. .![]() ______(2.17)
______(2.17)
[証明]. .1). .p=1 なら、. .![]()
2). .p=2 なら、 ![]()
3). .p=n のとき(2.17)が成立すると仮定すると、
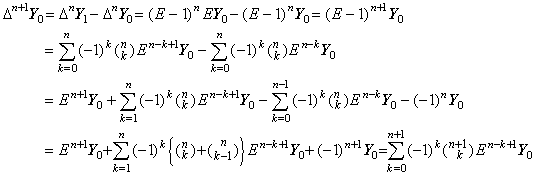
| [証明終] |
. . [定理 2.11]. .
[証明]. .1). .p=1 のとき、. .
2). .p=2 のとき、. .
3). .(2.18)は p=n のとき成立すると仮定すると、p=n+1 のときは、
. . [定理 2.12]. .n 階の階差演算子の逆演算子は陰関数により次のように表される。
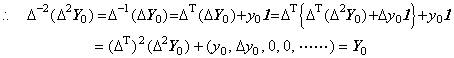
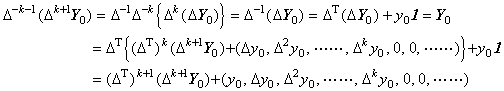
| [証明終] |
目 次 へ