3. 演算子法
1. ベクトル
1.1 ベクトルの定義
. .
等間隔点 tk=t0+kh, k=0, 1, 2, 3, ……, p における関数 y(t) の値が y0, y1, y2, y3, ………, ypであるとき、著者は(1.1)の右辺に示した階差の順序集合を t=t0における関数の順序集合と定義する。この順序集合は(1.1)の左辺のような太字の大文字又は小文字で表してよい。通常、混乱の恐れがないならその文字は順序集合の第1要素を示すであろう。
. . この順序集合は Newton の剰余項のない補間公式を表す。従って、y(t)の Newton の補間公式の剰余項が区間[t0, tp]において零か無視し得る値なら、この順序集合は y(t) に等価である。しかし、剰余項が無視できないなら、この順序集合は等間隔点 tkにおいてのみ y(t) に一致する。この順序集合は後退階差により定義することも出来るが、結果は同じことである。従って、著者は常に前進階差を用いる。
. . 関数 y(t) の t=t1における順序集合は添え字1を用いて定義され、区間[t1, tp+1]における Newton の剰余項のない補間公式を表す。一般に、関数 y(t) の t=tkにおける順序集合は添え字 k を用いて定義され、区間[tk, tp+k]における Newton の剰余項のない補間公式を表す。しかし、混乱の恐れがないなら添え字は省略してもよい。
. . 著者は、関数 y(t)の順序集合 Y0と関数 z(t)の順序集合 Z0の加算を関数の加算結果 y(t)+z(t)の順序集合として定義する。従って、和は(1.2)で表される順序集合となる。順序集合の減算も要素毎に減算した順序集合となる。この場合、減算結果の要素が全て零なら順序集合は零であると定義する。2つの関数が等間隔点 tk以外の全ての点で異なっていても、両者の階差は全て等しいから順序集合の減算結果は零である。この場合には、両順序集合は等しいと定義する。
. . α が任意の数であるとき、著者は順序集合 αY0を関数 αy(t)の順序集合と定義する。従って、それは α と順序集合 Y0の各要素の積を要素とする順序集合になる。
. . これらの定義により、任意の三つの関数の順序集合 W, Y, Zは以下に示すベクトル空間の条件を満たす。
| A. | . .全てのベクトル W, Y, Z について、 | |
| (A1). .Y+Z=Z+Y | (A2). .(Y+Z)+W=Y+(Z+W) | |
| (A3). .Y+0=Y なるベクトル 0 が存在する。 | ||
| (A4). .各ベクトル Y に対して Y+(−Y)=0 となるベクトル −Y が存在する。 | ||
| B. | . .全てのベクトル Y, Z 及びスカラー α, β に対して、 | |
| (B1). .1•Y=Y | (B2). .α(βY)=(αβ)Y | |
| (B3). .(α+β)Y=αY+βY | (B4). .α(Y+Z)=αY+αZ | |
. . 故に、この順序集合はベクトルである。著者はこれを第二種のベクトル又は点と呼ばれるベクトルと定義する。それは大括弧を用いて縦に表されるべきであるが、紙面の節約のため小括弧を用いて横方向に記述してよい。
. . 上記に定義したベクトルは、上記に述べたベクトルの加減算及びベクトルとスカラーの積を除き、力や速度や加速度等のよく知られたベクトルとは異なった特性及び量を持つ。よく知られたベクトルの大きさ、内積、及び、外積という概念は順序集合で表された関数の大きさや積の意味を持たないからここでは使わない。この順序集合の大きさや積については後で定義する。従って、今後、「通常の」というような語句を前後に伴わずに「ベクトル」という語が使われたとき、上記の順序集合の意味で使われているものとする。
1.2 ベクトル空間の性質
. .
(1.4)に示すように、1つの要素のみが零でなく、且つ、順序集合 Y0のそれぞれの要素に等しい順序集合で表された p+1 個のベクトルが存在する。その一次結合は α0, α1, α2, ……, αpをスカラーとして(1.5)で表される。零ベクトルの定義により、これらの係数が全て零のときのみこの一次結合は零である。従って、この p+1 個のベクトルは一次独立であり、ベクトル空間は p+1 次元空間である。ベクトル Y0はこの空間の点であり、全ての係数を1とした p+1 個のベクトルの一次結合である。この p+1 個のベクトルはベクトル Y0の要素である。
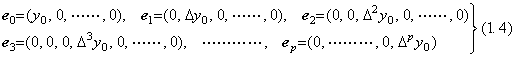
. . (1.4)の p+1 個のベクトルは(1.6)で表される関数を表すから、その大きさはそれぞれ(1.7)のノルムにより定義される。故に、これらの一次結合であるベクトル Y0のノルムは(1.8)により定義される。
. . これらの定義により、この空間の任意のベクトル Y 及び Z と任意のスカラー α について以下のノルム空間の条件が明らかに満足される。
| (N1) | ||Y || ≥0 | (N2) | ||Y ||=0. . ⇔ . .Y =0 |
| (N3) | ||αY ||=|α|•||Y || | (N4) | ||Y+Z || ≤ ||Y ||+||Z || |
. . この空間において、ベクトル(c, 0, 0, …… , 0)は定数関数を表し、ベクトル(y0, Δy0, 0, …… , 0)は一次関数を表し、ベクトル(y0, Δy0, Δ2y0, 0, …… , 0)は2次関数を表す。これらのベクトルはその末尾に値が零の要素をいくつ追加しても変わらない。関数が y=2tで t=nh であるときは、値が k=1, 2, …… に対して(2h−1)p+kである要素を追加しなければならない。p+1 番目迄の要素が以下のようになるからである。
従って、ベクトルは空間の次元数によって変わる。これらは有限小数と無限小数の関係に似ている。
. . もし、p+k+1 次元空間のベクトルの p+1 番目より後の要素が切り捨てられるなら、そのベクトルは p+1 次元空間に正射影される。何故なら、p+1 個の要素はその部分空間に存在するからである。Newton の補間公式の剰余項が無視し得ないなら、正射影されたベクトルは元のベクトルとは有意な違いを持つ。しかし、或るベクトル列が p+k+1 次元空間で連続であるなら、p+1 次元部分空間へ正射影されたベクトル列も連続である。それは3次元ユークリッド空間の点軌跡の2次元部分空間への正射影を考えれば明らかである。
. . 故に、全てのベクトルは同一次元の空間に存在するとして演算することが出来る。従って、ベクトル列が収束するなら、そのベクトル列は真の極限の p+1 次元空間への正射影に収束することを覚えておかねばならない。故に、極限 y(t) が Newton の補間公式で表され、その剰余項が無視できないなら、その関数列は極限 y(t) とは少し異なった関数に収束する。これが、区分幅 h が十分小さくない場合に、Milne 法のような微分方程式を解く従来の反復修正法が正しい解から少し異なった値に収束する理由である。
1.3 ベクトルの階差
. .
著者はベクトルの階差を2つのベクトル、即ち、関数 y(t)の t0におけるベクトル Y0と t1=t0+h におけるベクトル Y1の減算で定義する。それは(1.9)で表され、関数の減算で得られる関数 Δy(t)=y(t+h)−y(t)の t=t0におけるベクトルに等しい。それは Δ とベクトル Y0の要素の積を要素とするベクトルに等しく、第1要素が Δy0であるから ΔY0で表される。
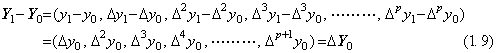
. . ベクトル Y0は区間[t0, tp+1]で定義されるから要素 Δp+1y0を持ち、従って、p+2 次元空間に存在する。一方、ベクトル Y1はこの区間では Δp+1y1を持たないから p+1 次元部分空間に存在する。従って、上記の減算は Y0の p+1 次元部分空間への正射影であるベクトルを用いて実行されねばならない。Y0のこの射影は最後の要素が切り捨てられただけであるから、混乱がない限り、又 Y0と表される。
. . 差分 ΔY0は2番目から p+2 番目迄の座標軸により構成される p+1 次元部分空間への Y0の正射影である。この正射影を最後の要素を切り捨てた Y0に対する演算 Δ と言う。故に、演算 Δ は最初の p+1 次元部分空間から2番目の p+1 次元部分空間への写像である。両部分空間のベクトルは p+2 次元空間のベクトル Y0の射影であるから y0は未知ではなく、従って、演算 Δ は可逆であり、ΔΔ−1=Δ−1Δ=1 である。
. . 演算 Δ は(1.1)の順序集合の全ての要素を1要素位置だけ左へシフトする演算に等価である。その際、Y0の最初の要素は取り除かれ、シフトの後 Δp+1y0が最後の要素として現れる。故に、(1, 2, 3, …… , 0)のようなベクトルがあったとき、演算 Δ は第1要素が第2座標軸の値であるベクトル(2, 3, …… , 0)を得るのであることを覚えておかねばならない。
. . 関数が区間[t0, tp+k]において y(t) であるとき、ベクトル Y0, Y1, Y2, …… , Ykがそれぞれ等間隔点 t0, t1, t2, …… , tkに存在する。従って、これらのベクトルは関数 Y(t)のこれら等間隔点における値であり、k 階の階差が次のように定義される。
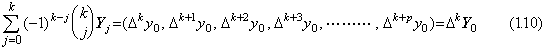
. . ベクトル ΔkY0は(1.11)で表される関数に等価であり、k+1 番目の座標軸から p+k+1 番目の座標軸で構成される最後の p+1 次元部分空間への Y0の正射影である。演算 Δkは最初の p+1 次元部分空間から最後の p+1 次元部分空間への写像である。ΔkY0の逆ベクトルは Y0の最初の p+1 次元部分空間への正射影である。従って、演算 Δkは可逆である。
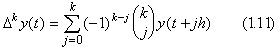
1.4 ベクトルの積
. .
著者は2つのベクトルY と Z の積を2つの関数の積のベクトル W として定義し、W=YZ と表す。
. . [定理 1.1]. .3つの関数の等間隔点 t0, t1, t2, …… , tpにおける値を y0, y1, y2, …… , yp 及び z0, z1, z2, …… , zp 及び w0, w1, w2, …… , wpで表すと、ベクトルの積 W=YZ は(1.12)の行列演算で表される。
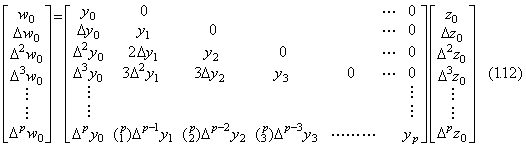
[証明]. .各行の証明は wk=ykzkの階差により与えられる。
1). .w0=y0z0.. .故に、第1行が成立する。
2). .
. .第2)項により、
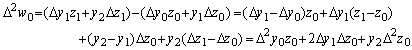
故に、第3行が成立する。
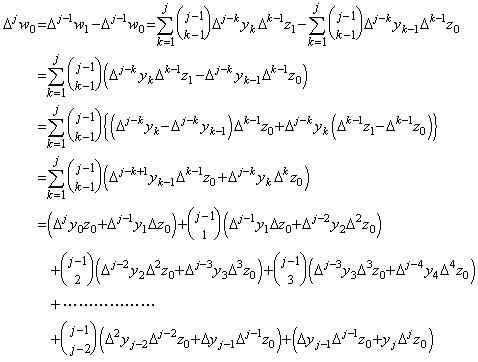
. . 各括弧内の右側の項とすぐ後ろの括弧内の左側の項を結合すると、k=1 から k=j−1 に対して、
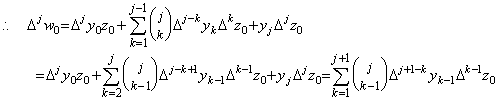
故に、第 j+1 行が成立する。________[証明終]
. .
(1.12)の行列は次のようにして得られる。関数値 yk−1を k 番目の対角要素に置き、対角要素より右にある全ての要素に零を置く。対角要素の左の要素に階差表を、第 j 行 k 列(k<j)要素の値が第 j 行 k+1 列の値から第 j−1 行 k 列の値を引いた階差になるように構成した後、第 j 行 k 列の値に2項係数 ![]() を掛ける。従って、その行列の第1列はベクトル Y を構成する。
を掛ける。従って、その行列の第1列はベクトル Y を構成する。
. .
ベクトルで演算を実行する演算子法の場合には、この行列は次の方法で求める。ベクトル Y を行列の第1列に置き、その右に、第 j 行 k 列(1<k≤j)に第 j−1 行 k−1 列の値と第 j 行 k−1 列の値の和を置く方法で階差表を構成した後、第 j 行 k 列の値に2項係数 ![]() を掛ける。
を掛ける。
. .
この行列はベクトルと同じであるが太字でない文字により表す。従って、ベクトルの積は(1.13)で表される。任意のベクトル Z≠0 に対して(Y−Y)Z=0 であるから行列 Y はベクトル Y に等価である。著者はこの行列をベクトルの展開と名付ける。
. .
[定理 1.2]. .全てのベクトル W, Y, Z について次の性質が成立する。
| (1) | YZ=ZY | (2) | (YZ)W=Y(ZW) | (3) | W(Y+Z)=WY+WZ |
[証明]. .(1)__ y(t)z(t)=z(t)y(t)___∴ YZ=ZY___∴ YZ=ZY
(2). .{y(t)z(t)}w(t)=y(t){z(t)w(t)}___∴ (YZ)W=Y(ZW)___∴ (YZ)W=Y(ZW)
(3). .w(t){y(t)+z(t)}=w(t)y(t)+w(t)z(t)___∴ W(Y+Z)=WY+WZ___∴ W(Y+Z)=WY+WZ
| [証明終] |
. .
交換則において、ベクトルの積が実行のために(1.12)で表されるとき、左側のベクトルが常に行列に展開されることに注意しなければならない。一方、(1.12)の行列とそれに続くベクトルの順序を入れ替える必要があるなら、両者は行列の積の反転則により転置しなければならない。
. .
スカラーと任意のベクトルの積 cY は主対角要素が全て定数 c である対角行列とベクトル Y の積として表せる。この対角行列は定数関数を表すベクトル C=(c, 0, 0, ……)を展開した行列に等価である。故に、積 cY はベクトルの積 CY で表すことができる。即ち、本演算子法ではスカラーを定数ベクトルと区別する必要はない。従って、著者は今後、スカラーとベクトルの積という概念は使用しない。
. .
しかし、ベクトル C が定数又は定数関数であることを明瞭に示したいなら cY という表記を用いる。この場合、記号 c はベクトル C が展開された行列を示す。この表記は任意の行列を示すときも使われる。
. .
ベクトル 1 でベクトル(1, 0, ……, 0)を表すと、任意の定数ベクトルは c1 と表すことが出来る。この表記は、微分方程式の解を行列演算で表すとき初期値を y01 で表すために使われる。何故なら、定数ベクトル(y0, 0, 0, ……)を(1.1)のベクトル Y0とベクトルの表記規則では区別できないからである。
. .
(1.12)に Z=1 を代入すると、任意のベクトル Y は Y=Y1 と表される。従って、著者はベクトル 1 を単位ベクトルと名付ける。Y1=1Y であるからベクトル 1 は単位行列に展開できる。
. .
[定理 1.3]. .W=YZ のとき、これらのベクトルを展開した行列 W, Y, Z の間に等式 W=YZ が成立する。
[証明]. .行列 C で Y と Z の積を表すと、行列 C はベクトル W を展開した行列 W に等しいことを示す。
. .
行列 C,Y,Z の要素をそれぞれ cjk, ajm, bmk, ( j, k, m≥1)で表すと、要素 ajm は m>j のとき全て零であり、要素 bmk は m<k のとき全て零である。従って、行列 C は k>j の要素が全て零の三角行列である。何故なら、ajm と bmk の積において m≥k に対しては m>j だからである。k≤j の場合は、ベクトル W, Y, Z が表す関数の値をそれぞれ wj−1, ym−1, zk−1 で表すと、
. . k=1 の場合は、定理 1.1 により(1.14)の右辺は積 YZ の第 j 番目の要素に等しいから、要素 cj1 は行列 W の第 j 行1列の要素に等しい。
. . k≥2 の場合は、証明は主対角要素に平行にある要素からなるグループ毎に与える。
| 1) | . .k=j の場合は m=j だけであるから(1.14)は cjj=yj−1zj−1=wj−1となる。これは行列 W の主対角要素の j 番目の要素に等しい。 | ||
| 2) | . .k=j−1 の場合は、 m=j−1=k と m=j=k+1 であるから、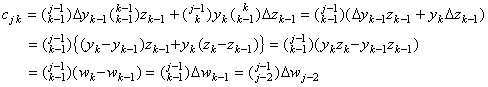 これは行列 W の主対角要素の左の要素に等しい。 | ||
| 3) | . .k=j−2 の場合は、m=k, k+1, k+2 であるから、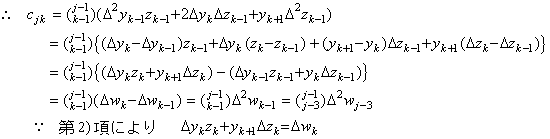 従って、cjk は行列 W の第 j 行 j−2 列に等しい。 | ||
| 4) | . .k=j−n のとき、cjk は行列 W の第 j 行 k 列に等しいと仮定すると、 . . k=j−(n+1) のときは m の値は u=0 から u=n+1 に対して m=k+u であり、且つ、 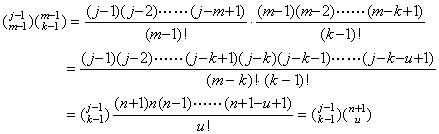 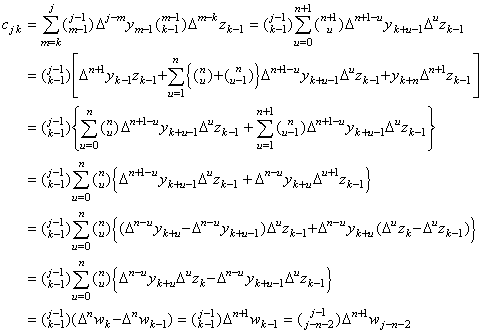
|
. . ベクトルの積 YZ は交換可能であるけれども、ベクトル Y が行列 Y に展開されると積 YZ は交換可能ではない。しかし、両ベクトルが行列に展開されると積 YZ は交換可能である。それは定理 1.3 の記号 y と z を入れ替えることにより容易に証明できる。これらは、ベクトルを展開した行列はベクトルのより多くの特性や量を明示的に表示していることをのぞき、ベクトルと等価であることを示す。両者の関係は分数と少数の関係に類似である。
1.5 ベクトルの商
. .
等式 W=YZ が成立するとき、著者は被乗数、即ち、ベクトル Y をベクトル W と Z の商と定義し、Y=W/Z で表す。ベクトル W は定理 1.2 により等式 W=ZY で表すことも出来る。この場合、ベクトル Z がベクトル W と Y の商であり、Z=W/Y と表される。商 1/Y がベクトルなら、著者はそれを Y の逆ベクトルと呼び、ベクトル Z を Z=W(1/Y)=(1/Y)W とも表す。又、逆ベクトルを Y−1 とも表し、演算 W=YZ の逆演算 Z=Y−1W に用いたときこれを逆商と呼ぶ。
. .
関数 y(t)の値 yk が零でないなら、関数 z(t)=w(t)/y(t) の t=tk における値、zk=wk/yk で表される値 zk が存在する。区分幅 h の等間隔点 t0, t1, t2, ……, tp に対して z0 から zp 迄の値が全て存在するなら、それらの階差で構成されるベクトル Z がベクトル W と Y の商である。又、 zk=wk(1/yk) であるから、商 Z はベクトル W と 1/y0 から 1/yp 迄の階差で構成されるベクトルの積により求めることが出来る。逆ベクトル Y−1 はこの 1/yk の階差で構成されるベクトルである。従って、商及び逆ベクトルが存在する必要十分条件は、ベクトル Y を展開した行列 Y の対角要素に零がないことだから行列式 det(Y)≠0 である。
. .
[定理 1.4]. .
逆ベクトル Y−1 は一意であり、その要素は以下に示される。但し、Y1k はベクトル Y を展開した行列 Y の行列式の第1行第 k 列の要素の余因子を示し、det(Y)は行列 Y の行列式を示す。
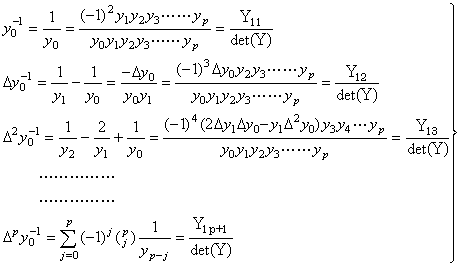 (1.15)
(1.15)[証明]. . 全ての対角要素が yk≠0 であることにより det(Y)≠0 であるから、逆行列 Y−1 が一意に存在する。ベクトル Z で 1/yk の階差で構成されるベクトルを表すと、yk(1/yk)=1 であるから、
| YZ=1 | ∴. .YZ=1 | ∴. .Z=Y−11 |
. .[定理 1.5]. .
逆行列 Y−1 を展開した行列はベクトル Y を展開した行列 Y の逆行列である。
[証明]. .det(Y)≠0 であるから、逆行列 Y−1 が一意に存在する。Z で逆ベクトル Y−1 を展開した行列を表す。YY−1=1 であること及び、定理 1.3 により、
| YZ=1 | ∴. .Z=Y−1 | [証明終] |
1.6 ベクトルの商の拡張定義
. .
関数の或る値 yk が零なら、階差を 1/yk=∞ の点で計算不可能であるから、ベクトル Y による商も逆ベクトル Y−1 も存在しない。関数 y(t)が区間[t0, tp]において t 軸と交差するとこのようなことが起こる。しかし、交差点を含まないように区間に制限をつけるか、等間隔点間の区分幅 h をどの点も交差点に一致しないように調節するなら、そのベクトルによる商も逆ベクトルも存在することになる。区間[t0, tp]における関数のベクトル Y による商の存在に関する特性が等間隔区分幅の値により変わるということは不便である。それで、著者はそのような場合にも商が存在するように商の定義を拡張する。
. .
関数の値 yk が零のとき、積 wk=zkyk は一意に零であり、従って、ベクトル W は W=ZY により一意に決まる。この場合に、著者は、商 Z は一意に存在すると定義し、商を Z=W/Y で表す。定義により、ベクトル Y を展開した行列 Y の det(Y) が零でもベクトル Y が零でないなら商が存在する。故に、商は数の商に類似となるが、逆ベクトルが存在するためには積 W は単位ベクトル 1 でなければならないのに wk=zk×0≠1 であるから、ベクトル Y の逆ベクトルは存在しない。しかし、Y/Y=1 は商の定義 Y=1Y により det(Y) が零でも成立するから、商を 1/Y 又は Y−1 による積で表すことは認められる。故に、
. . 拡張されたベクトルの商を使用する式は ZY=W 又は Y/Y=1 を用いて変形してよい。又、関数値 wk, yk が零となる tk における関数値 zk が既知なら zn=wn/yn の階差でベクトルを構成することも出来る。それが既知でないなら zk=0/0 の値は不定だから商 Z は不定である。即ち、拡張された商は W=ZY で表される変換されたベクトル W の元ベクトル Z を意味し、任意の2つのベクトルの商 W/Y を意味するのではない。それ故、拡張された商は一意であり、演算 W=YZ の逆演算として Z=Y−1W と表すことが認められる。従って、Y−1 の表記は逆商であって、逆ベクトルではない。拡張された商の一意性は微分方程式が初期値が既知のとき一意の解を持つことに類似である。
. . det(Y)=0 のとき、連立方程式 YZ=0 は零でない解を持つことはよく知られている。その解を Za で表せば、
| W=Y(Z+Za)=Y(Z+Za)=(Z+Za)Y | (1.16) |
. . 或る点 tk に対して yk=0 なら、如何なる za に対しても wk=(zk+za)yk の値は零である。その点 tk が微小な値 ε だけ、関数 y(t) が t 軸と交わる点 ta からずれるような値に等間隔区分幅 h を変えるなら、zk=wk/yk の値は一意になるから za の値は零になるに違いない。従って、関数 za(t) は za(t) が不定である点 ta 以外の全ての点で零である。即ち、tk=ta 且つ za(ta)≠0 であるなら、関数 za(t) 及び z(t)+za(t) は点 tk において不連続である。za(ta)=0 なら(1.16)は商 W/Y としてベクトル Z だけを持つ。その条件は z(tk) の値が既知であることである。
. . 故に、著者の演算子法は拡張された商を使用するとき、関数は連続であることを要する。表に表された関数は Newton の補間公式で表せればこの条件を満たすことが出来る。Newton の補間公式は表で表された関数を連続関数に変換するものである。従って、これらの関数において Y≠0 且つ YZ=0 なら商 0/Y は Z=0 のみであり、Y=0 なら、関数値が全て既知である関数を求めることは意味がないので商は存在しない。故に、任意のベクトルをベクトル 0 で割ることは認められない。更に、YZ=0 ならベクトル Y か Z のどちらかは零である。
. .
[定理 1.6]. .商及び拡張された商 Z=W/Y は次の行列演算で表される。
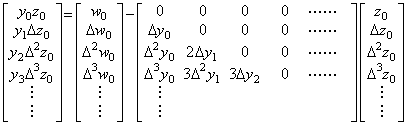 . .(1.17)
. .(1.17)| [証明] | W=ZY=YZ=YZ | ∴ | YZ=W |
. . ベクトル Z の要素が(1.17)の両辺にあるけれど、それらは反復法により次のように容易に求められる。
| 1) | (1.17)の第1行は y0z0=w0 を与える。故に、z0=w0/y0 |
| 2) | これを右辺の Z に代入すると、第2行から、 |
| 3) | これを右辺の Z に代入すると、第3行から、 |
| 4) | 同様にして、 |
| 5) | その他の高階の階差は同様の方法で全て得られる。 |
. . もし、y2 が零なら、z2 の値は与えられていなければならず、上記の 3) の代わりに Δ2z0 の値は上記で得られた z0, Δz0 及び与えられた z2 を用いて計算されねばならない。この場合、z2 の値の代わりに Δ2z0 の値が既知でも良い。もしそうなら、上記の 3) は単にとばせばよい。
1.7 ベクトル値関数
. .
連続関数 y(t) があるとき、等間隔区分点 tk=t0+kh にそれぞれ第1要素が y(t0), y(t1), y(t2), …… であるベクトル Y0, Y1, Y2, …… が存在する。更に、任意の点 t に第1要素が y(t) であるベクトル Y が連続的に存在する。この最初の点を x0 で表せば、等間隔区分点は k=0, 1, 2, ……, p に対して xk=x0+kh で表される。従って、それらは p+1 個の要素を持つ次のベクトルで表される。ベクトル Y も同じ個数の要素を持つ。
| X=(x0, h, 0, ……, 0) | (1.18) |
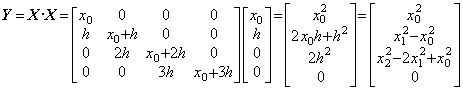 . .(1.19)
. .(1.19)| Y=Y(X)=X 2 | (1.20) |
. . 関数 Y=F(X) があるとき、逆に、ベクトル Y に対するベクトル X を与える関数が存在する。それは逆関数と呼ばれ、X=F −1(Y) と表される。逆関数は、等間隔区分幅は関数 Y=F(X) と同じでなければならないから一意である。故に、h の値が正なら(1.20)の逆関数は次のようになる。
 . .
t=x0 におけるベクトル X は(1.18)で表されるが、t=−x0 におけるベクトルは次のようになる。
. .
t=x0 におけるベクトル X は(1.18)で表されるが、t=−x0 におけるベクトルは次のようになる。| X−=(−x0, h, 0, ……, 0) | (1.22) |
| −X=(−x0, −h, 0, ……, 0) | (1.23) |
. . h<0 の場合、ベクトル X も Y も後退差分で構成されているので逆関数は次のようになる。
. . Y の平方根のベクトル値は(1.21)の Taylor 展開又は y0, y1, y2, ……, yp の平方根の階差を用いて求めることが出来る。又、Newton-Raphson 法を用いたベクトル計算により得ることも出来る。そのプログラム及び結果は第 4 章の第 1.6 節及び第 3.2 節に述べられる。
1.8 ベクトルの絶対値
. .
ベクトル![]() が存在する条件は
が存在する条件は![]() の値が全て存在することである。従って、ベクトル Y が定義されている範囲の全ての k に対して条件 yk≥0 が満たされねばならない。この場合、第1要素以外の符号は関数の形に依存するので、全ての yk の値がその条件を満たしているか否かを要素の符号から直接判断することは常には出来ない。ベクトル Y を展開した行列の主対角要素の符号を全て調べることが必要である。全ての対角要素が零以上ならベクトル Y の平方根は存在する。
の値が全て存在することである。従って、ベクトル Y が定義されている範囲の全ての k に対して条件 yk≥0 が満たされねばならない。この場合、第1要素以外の符号は関数の形に依存するので、全ての yk の値がその条件を満たしているか否かを要素の符号から直接判断することは常には出来ない。ベクトル Y を展開した行列の主対角要素の符号を全て調べることが必要である。全ての対角要素が零以上ならベクトル Y の平方根は存在する。
. .
故に、著者はその場合に Y≥0 であると定義する。対角要素が全て零より小なら Y<0 と定義する。従って、正でも零でも負でもないベクトルが存在することを覚えておく必要がある。このようなベクトルはその定義範囲において関数 y(t) が t 軸と交差していることを示す。区分幅 h→0 の極限ではこのようなベクトルは消える。
. .
ベクトルの絶対値は正又は零のベクトル値として定義しなければならない。関数の絶対値 |y(t)| は又 t に関する関数であり、その関数を変換したベクトルが存在する。著者はそのベクトルを Y の絶対値と定義し、|Y| と表す。従来のベクトルの絶対値の概念はこの意味を持たないから本演算子法では使用しない。
. .
ベクトル |Y| を行列に変換するなら、定義により主対角要素は関数値の絶対値 |yk| であり、その他の要素は第 1.4 節で述べた展開法により構成される。その第1列はベクトル |Y| であり、ベクトル |Y| の第1要素は |y0| であるから正であるが、他の要素が正であるか否かは関数
. .
要素があるベクトル Y の要素の絶対値であるベクトルは正である。しかし、そのベクトルと |Y| の関係は(1.25)で表される。
| . .[定理 1.7]. . | (1.25) |
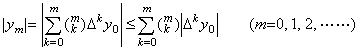 _____[証明終]
_____[証明終]. . 通常のベクトルでは、絶対値はベクトルの大きさである。しかし、本演算子法では大きさを表さず、絶対値を値とする関数を表す。従って、任意の2つのベクトル Y, Z があるとき、定理 1.7 に述べたような特別な条件を満たす場合以外、Y−Z 又は |Y|−|Z| によりどちらのベクトルが大きいかを判断することは常には可能でない。それは関数のノルムにより判断しなければならない。それがベクトルの大きさを関数のノルムにより定義する理由である。
. . 関数のノルムは通常はどの等間隔区分点における関数値の絶対値より大きいかもしれない。しかし、等間隔区分幅が十分に小さければノルムがどれかの区分点における関数の絶対値に与えられた精度で等しくなるだろうということは認め得るであろう。従って、ベクトルのノルムはベクトルを展開した行列の主対角要素の絶対値の最大値であると定義できる。従って、どちらのベクトルが大きいかは2つのベクトルを行列に展開することにより判断される。 目 次 へ