3. Impulsive response of Transfer function by Differential equation.
3.1 Introduction.
. .
The author made an attempt at obtaining the impulsive response of transfer function by use of the numerical solution of differential equation, because he thought that the method might be better and more simple than inverse Laplace transformation in case of higher-order system. However the attempt had to solve the two problems which are as for the accuracy of numerical calculus and the value at t=0 for Laplace transformed function. The work came to introduction of the operational calculus and the rigorous definition of Laplace transform.
. .
The Laplace transform of the derivative of f(t) is expressed in Eq.(3.1) so it should be the same with the derivative of impulse function. However Laplace transform makes an exception of the relation in Eq.(3.2) because
| L f ' (t)=sL f(t)−f(0) | (3.1) | L δ' (t)=s L δ(t)−δ(0) | (3.2) |
3.2 Impulse function.
. .
The Dirac delta function does not satisfy Eq.(3.2) because δ(0) is infinite. The impulse function should have zero for
. .
[Definition 1]. .
![]()
. .
The impulse function starts up increasing at t=0 and reaches to the peak at tp=nε then decreases as an exponential function. Its integrated value is always unity for any value ε.
| tp→+0, |
| δ(tp+0)→0, | δ(0)=0 | (3.5) |
| . . [Theorem 3.1] | f(t)δ(t)=f(0)δ(t), | if f(+0) is equal to f(0). | (3.7) |
|
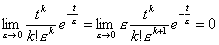
| for k=0, 1, 2, …… |
| ∴ f(t)δ(t)=f(0)δ(t) | [Q.E.D.] |
. .
In the case of δ(t−d), the impulse function has the peak at tp=d+0 and is zero everywhere except at t=tp. Its integrated value is unity and it is evident that
| f(t)δ(t−d)=f(d)δ(t−d) | (3.8) |
| L δ(t−d)=e−sd | (3.9) |
3.3 Unit step function.
. .
The unit step function must be the integral of the impulse function over the range zero to t with zero for
. .
[Definition 2]
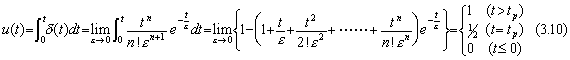
. .
By the definition, the Laplace transform of unit step function is
. .The value may be one half of the integral of impulse function because that
|
| ∴ 2u(tp)δ(t)=δ(t) | ∴ 2u(tp)=1 |
| . . [Theorem 3.2] |
| __________={F(t)−F(d)}u(t−d) | [Q.E.D.] |
. .
By substituting e−st for f(t) and limiting t→∞, the Laplace transform of u(t−d) is
| Hence u(t−d) is the convolution integral of u(t) and δ(t−d). |
3.4 Laplace transform of any function.
. .
If f(t) is a known function for t>0 and zero for t≤0, the Laplace transform is defined by the equation
. .
[Definition 3]. . The Laplace transform is the Fourier transform of the function f(t) multiplied by u(t)e−at, where f(t) is not always zero for t≤0, that is,
. . By the definition, the Laplace transformable function should be rigorously expressed in f(t)u(t). Although the unit step function has no effect on the integral of Eq.(3.16), it is very important in order to express transfer functions in the differential equations because the function f(t) multiplied by u(t) is the reason why the integral operation after differentiation is reversible in Laplace transform. Also in the original plane, the integral operation after differentiation of f(t)u(t) is reversible because of
| sL f(t)u(t)=L f ' (t)u(t)+f(0) | (3.20) |
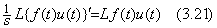
|
. . Eq.(3.20) must be used in order to transform the differential equation with initial values into the Laplace transform. However in order to transform any transfer function into the differential equation, Eq.(3.21) must be used because all the initial values of f(t) and its derivatives are not given explicitly.
| . .[Theorem 3.3] | L {f(t)u(t)}(n)=snL f(t)u(t) | (3.22) |
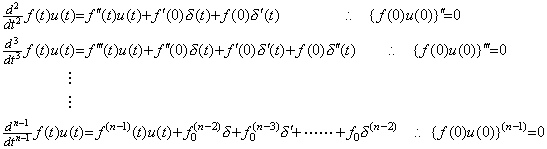
| L {f(t)u(t)}(n)=sL {f•u}(n−1)=s2L {f•u}(n−2)=……=snL {f•u} | [Q.E.D.] |
3.5 Laplace transform and Fourier transform.
. .
The function u(t)e−at in Eq.(3.17) picks up the portion of the function f(t) from zero to about 1/a for t so it is required that the value a is positive and greater than the value b if the function f(t) is ebt, where it is the conditions for the existence of the integral from zero to infinite. Therefore the Laplace transform represents the frequency response of the portion.
. .
If the function f(t) with zero for t≤0 is shifted from t to t+d, the Laplace transform is expressed in Eq.(3.23). It represents that f(t−d) is the convolution integral of f(t) and δ(t−d). In case of a=0, It represents that the Fourier transform does not vary with the value d except the phase response. On the other hand, the magnitude response of the Laplace transform is e−ad times that of Eq.(3.16).
| f(t)u(t)=t2u(t)−(t−1)2u(t−1) |
. . On the other hand, letting s=a+jω and a »1,
|
| because of | (3.26) |
. . The frequency response Eq.(3.26) is significant over the range of t<1 and the frequency response for t≥1 is obtained by Eq.(3.24).
. . Therefore the Fourier transform picks up the similar characteristic between the two portions and represents the abstractive idea which requires a good knowledge of superposition in order to understand that it represents the combination of two functions. On the other hand, the Laplace transform is a local frequency response and picks up the different characteristic between the two portions. The author thinks that the response is similar to the sense of sight.
. . The Laplace transform is also very useful for analyzing the phenomena with the frequency response which varies according to time as voice. However, if the position of the combination is explicit, the analysis is very easy. The author thinks that voice has the pitch cycle for the purpose of showing the position.
. . Usually, the filter is operated by the technique of convolution integral. However above mentioned filter must not be operated by the technique because its Laplace transform is (s+a)−1, that is, low pass filter and the operated results are very different from the results of the human sense which senses strong response for higher frequency in narrow time width.
3.6 Impulsive response and its differential equation.
. .
When y(t) is the impulsive response of a transfer function expressed in Eq.(3.28), the values for t≤0 are all zero because the values of input function for t≤0 are all zero. Therefore y(t) is expressed in Eq.(3.29) because the transfer function has the coefficient bn, if it is not zero. δ(0) to δ(n−1)(0) are all zero by Definition 1 for δ(t) then y(0) to y(n−1)(0) are all zero from the proof of Theorem 3.3. Hence Eq.(3.28) is transformed into the differential equation expressed in Eq.(3.30) by Theorem 3.3.
| Y(s)= | bnsn+bn−1sn−1+bn−2sn−2+………+b0 sn+an−1sn−1+an−2sn−2+………+a0 | •1 | (3.28) | y=z(t)u(t)+bnδ(t) | (3.29) |
| y(n)+an−1y(n−1)+an−2y(n−2)+………+a0y=bnδ(n)+bn−1δ(n−1)+bn−2δ(n−2)+………+b0δ | (3.30) |
. . The differential equation can analytically be solved by the technique of letting ε→0 after having obtained the solution of the differential equation which is substituted the impulse function before letting ε→0. In usual definition for δ(t), the technique can not be used except of the differential equation with only the right-hand member of b0δ(t).
. . When an impulsive response is expressed in Eq.(3.31), it is transformed into the differential equation with initial values
| Y(s)= | s+1999 s2+1001s+1000 | •1 | (3.31) | y" +1001y' +1000y=δ' (t)+1999δ(t) | (3.32) |
| δ' (t)+1999δ(t)= | 1 ε2 |
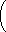 |
1− | t ε |
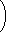 e e |
−t ε |
+ | 1999t ε2 | e | −t ε |
(3.33) |
y=Ae−t+Be−1000t+C1e | −t ε | +C2te |
−t ε |
A= | 2 (ε−1)2 | B= | −1 (1000ε−1)2 | (t≥0) | (3.34) | |||
| , | , | , |
C1= | −1999999ε2+3998ε−1 (1000ε−1)2(ε−1)2 | , | C2= | 1999ε−1 ε(1000ε−1)(ε−1) | (3.35) |
. . The particular integral must satisfy the differential equation then the constants C1 and C2 are expressed in Eqs.(3.35). Hence the constants A and B are determined by the initial values y(0)=y' (0)=0. By letting ε→0, these constants are A→2, B→−1, C1→−1, εC2→−1 and the particular integral converges to −1 for t=0 and 0 for t>0.
. . Hence the solution converges to the complementary function for t>0 and zero for t≤0, that is, y=z(t)u(t), where z(t) is the complementary function. The solution is equivalent to the inverse Laplace transform of Y(s). Therefore the impulsive response can be obtained easily by solving the homogeneous differential equation with right-hand member equal to zero. However the initial values are not all zero. The homogeneous differential equation is expressed as follows.
| z" +1001z' +1000z=0 | , | z(0)=1 | , | z' (0)=998 | (3.36) |
. . The reason for y(0)=0 is that z(0) is cancelled by the initial value of the particular integral and the reason for
. .
[Theorem 3.4]. .
When y(t)=z(t)u(t)+kδ(t) is the solution of the differential equation in Eq.(3.30), z(t) is expressed in the homogeneous differential equation Eq.(3.37) with the initial values in Eq.(3.38).
| z(n)+an−1z(n−1)+an−2z(n−2)+………+a0z=0 | (3.37) |
  | a0 | a1 | a2 |  | an−1 | 1 |   |   | k |   | = |   | b0 |   | (3.38) |
| a1 | a2 |  | an−1 | 1 | 0 | z0 | b1 | ||||||||
| a2 |  | an−1 | 1 | 0 | 0 | z0' | b2 | ||||||||
 |  |  |  | ||||||||||||
| an−1 | 1 | 0 |  | 0 | z0(n−2) | bn−1 | |||||||||
| 1 | 0 |  | 0 | z0(n−1) | bn |
| y(t)= | z(t)u(t)+kδ(t) |
| y' (t)= | z' (t)u(t)+z0δ+kδ' |
| y" (t)= | z" (t)u(t)+z0' δ+z0δ' +kδ" |
| y(3)= | z(3)•u(t)+z0" δ+z0' δ' +z0δ" +kδ(3) |
 | |
| y(n)= | z(n)u(t)+z0(n−1)δ+  +z0δ(n−1)+kδ(n) +z0δ(n−1)+kδ(n) |
| [Q.E.D.] |
. . In case of the differential equation in Eq.(3.32), the value n is equal to 2 and the initial values in Eqs.(3.36) are obtained as follows.
  | 1000 | 1001 | 1 |   |   | k |   | = |   | 1999 |   |
| 1001 | 1 | 0 | z0 | 1 | |||||||
| 1 | 0 | 0 | z0' | 0 | |||||||
| ∴ | k=0, | z0=1, | z0' =998 | ||||||||
| Y(s)= | Ts Ts+1 | •1 | y' + | 1 T | y=δ' (t) | (3.39) |
  |
1 T | . .1 |   |
  | k |   | = |   | 0 |   |
∴ | k=1, | z0= | −1 T | ∴ | y= | −1 T | e | −t T | u(t)+δ(t) | (3.40) |
| 1 | . .0 | z0 | 1 |
| y' + | 1 T | y=δ' (t)+ | 1 T | 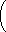 | 1−e | −t T | 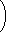 | δ(t) | (3.41) |
. . In Laplace transform, the numerator may be divided by the denominator and the transfer function is expressed in
  | a0 | a1 | a2 |  | an−1 | 1 |   |   | 0 |   | = |   | b0 |   |
−k |   | a0 |   |
(3.42) |
| a1 | a2 |  | an−1 | 1 | 0 | z0 | b1 | a1 | |||||||||||
| a2 |  | an−1 | 1 | 0 | 0 | z0' | b2 | a2 | |||||||||||
 |  |  |  |  | |||||||||||||||
| an−1 | 1 | 0 |  | 0 | z0(n−2) | bn−1 | an−1 | ||||||||||||
| 1 | 0 |  | 0 | z0(n−1) | bn | 1 |
3.7 The numerical simulator of impulsive response.
. .
Any impulsive response is obtained by the numerical solution of differential equation, because it is able to transform the impulsive response of any transfer function into the homogeneous differential equation with the initial values by Theorem 3.4. So the numerical solution of differential equation is the simulator of any impulsive response. This is very simple and easy method because it does not use the poles of Laplace transform Y(s).
. .
The inverse Laplace transformation requires the numerical method obtaining the poles, the partial fraction expansion of
. .
When Y(s) is expressed in Eq.(3.43), Eq.(3.44) is the numerical expression in single precision. The discriminant D2 has the negative value depending on the rounded errors of two constants at least significant bit by binary system. The shown value is the result of BASIC program given below. Therefore the numerical poles are not double pole but a pair of complex poles and the inverse Laplace transform comes to Eq.(3.45), if the difference of nearly equal complex numbers is obtained correctly without cancellation. It is very different from the analytical result in Eq.(3.46).
| Y(s)= | 1 s2+(44/7)s+(484/49) | (3.43) | Y(s)= | 1 s2+6.285714s+9.877551 | (3.44) |
| D2=6.2857142−4×9.877551=−3.814697×10−6 | jω=D/2=9.765625×10−4j |
| B=44/7:C=484/49:D2=B*B−4*C:D=SQR(−D2) | |
| y= | 1 ω | e−3.142857tsinωt | (3.45) | yt=te | −22t 7 | (3.46) |
. . When Y(s) is expressed in Eq.(3.47), Eq.(3.48) is the numerical expression in single precision. The discriminant D2 has the positive value by BASIC program given below. Therefore the numerical poles are not double pole but two nearly equal poles and the inverse Laplace transform comes to Eq.(3.49). It is very different from the analytical result in Eq.(3.50).
| Y(s)= | 1 s2+(72/13)s+(1296/169) | (3.47) | Y(s)= | 1 s2+5.538462s+7.668639 | (3.48) |
| D2=5.5384622−4×7.668639=1.907349×10−6 | D=1.381068×10−3 |
| B=72/13:C=1296/169:D2=B*B−4*C:D=SQR(D2) | |
| y= | 1 D |  e−2.768540t−e−2.769921t e−2.768540t−e−2.769921t | (3.49) | yt=te | −36t 13 | (3.50) |
. . Table 3.1 and 3.2 shows above results and the results of the numerical simulator, that is, the numerical solution of differential equation by the variable pitch method using 3 points. The method using the numerical solution of differential equation has not these troubles because it does not use any pole. It is farther very simple and easy in case of higher order transfer function.
. . The subroutines of Program 2.2 are represented as follows. The values BB and CC in line 56 must be given in line 58. If the values are expressed as decimal numbers in line 56, it follows that the solution has larger error.
| Subroutines for Eq.(3.43) |
|---|
| 56 F=−BB*Y(2)−CC*Y(1):RETURN 58 XB=0:XE=30:N=300:ND=2:Y(2)=1:Y(1)=0:BB=44/7:CC=484/49:B2#=22#/7#:RETURN 60 Y#=X#*EXP(−B2#*X#):RETURN |
| Subroutine for Eq.(3.47) |
| 58 XB=0:XE=30:N=300:ND=2:Y(2)=1:Y(1)=0:BB=72/13:CC=1296/169:B2#=36#/13#:RETURN |
| Table 3.2 The case D2>0 by rounded error. | ||||||
|---|---|---|---|---|---|---|
| IB | EE | t | Laplace | Simulator | Accurate | exp |
| 1 2 3 4 5 6 7 8 9 10 15 20 25 30 35 40 45 50 60 70 80 90 100 150 200 250 260 270 280 290 300 |
4 8 8 16 8 8 8 4 4 4 4 2 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 6.0 7.0 8.0 9.0 10.0 15.0 20.0 25.0 26.0 27.0 28.0 29.0 30.0 |
7.5829260 1.1493075 1.3070513 1.3215093 1.2518086 1.1388416 1.0074244 8.7298602 7.4442796 6.2703721 2.3553682 7.8642648 2.4618818 7.3976151 2.1610798 6.1853134 1.7424429 4.8490278 3.6486452 2.6692597 1.9131514 1.3496389 9.4054035 1.3681575 1.7693020 2.1450040 1.3987099 9.1085960 5.9234641 3.8477601 2.4961132 |
7.5811274 1.1494700 1.3071419 1.3212813 1.2521005 1.1390801 1.0074764 8.7289229 7.4446961 6.2710218 2.3555843 7.8651421 2.4619882 7.3983805 2.1614885 6.1860657 1.7427557 4.8491265 3.6490809 2.6697400 1.9133717 1.3498644 9.4055813 1.3682550 1.7692994 2.1449140 1.3988892 9.1099043 5.9244493 3.8479376 2.4962690 |
7.58112819 1.14947008 1.30714199 1.32128144 1.25210048 1.13908007 1.00747644 8.72892306 7.44469664 6.27102248 2.35558508 7.86514460 2.46198784 7.39837479 2.16148535 6.18604995 1.74275013 4.84910729 3.64906330 2.66972510 1.91336070 1.34985690 9.40553661 1.36825368 1.76928238 2.14486002 1.39884840 9.10960246 5.92423189 3.84778125 2.49615753 |
-02 -01 -01 -01 -01 -01 -01 -02 -02 -02 -02 -03 -03 -04 -04 -05 -05 -06 -07 -08 -09 -10 -12 -17 -23 -29 -30 -32 -33 -34 -35 |
| Table 3.1 The case D2<0 by rounded error. | ||||||
|---|---|---|---|---|---|---|
| IB | EE | t | Laplace | Simulator | Accurate | exp |
| 1 2 3 4 5 6 7 8 9 10 15 20 25 30 35 40 45 50 60 70 80 90 100 150 200 250 260 270 272 |
8 8 8 8 8 8 8 4 4 4 4 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 6.0 7.0 8.0 9.0 10.0 15.0 20.0 25.0 26.0 27.0 27.2 |
7.3031031 1.0667063 1.1685400 1.1378624 1.0387408 9.1032371 7.7562213 6.4736538 5.3187482 4.3159299 1.3449397 3.7254493 9.6744415 2.4118152 5.8455844 1.3878954 3.2437426 7.4875703 3.8778914 1.9526134 9.6312208 4.6763544 2.2425307 5.0372520 1.0057567 1.8826088 8.4501330 3.7872693 0.0000000 |
7.3031038 1.0667065 1.1685402 1.1378627 1.0387410 9.1032393 7.7562220 6.4736553 5.3187493 4.3159310 1.3449405 3.7254544 9.6744596 2.4118229 5.8456051 1.3879015 3.2437570 7.4876061 3.8779149 1.9526267 9.6313131 4.6764090 2.2425613 5.0374123 1.0058035 1.8827438 8.4508017 3.7875821 2.0350776 |
7.30310346 1.06670639 1.16854005 1.13786250 1.03874094 9.10323861 7.75622124 6.47365522 5.31874923 4.31593093 1.34494024 3.72545195 9.67444862 2.41181899 5.84559528 1.38789922 3.24375241 7.48759648 3.87791391 1.95262767 9.63132129 4.67641321 2.24256404 5.03742439 1.00581870 1.88279114 8.45103635 3.78769387 2.03513807 |
-02 -01 -01 -01 -01 -02 -02 -02 -02 -02 -02 -03 -04 -04 -05 -05 -06 -07 -08 -09 -11 -12 -13 -20 -26 -33 -35 -36 -36 |
Continued to. .3.8 The problem having to be cautioned.