. . It is able to transform any homogeneous differential equation with the initial values into the transfer function also by Theorem 3.4. Therefore the numerical simulator may have such troubles that some impulsive responses are not obtained exactly up to far point from t=0 as mentioned in the numerical solution of differential equations.
. . When the differential equation is z" +3z' +2z=0 with z(0)=1 and z' (0)=−2, the Laplace transform of y(t)=z(t)u(t) is expressed in Eq.(3.51) by Theorem 3.4 and k=0. The numerical simulator can not obtain the exact result up to large t in case of no cancellation with s+1 in the numerator and denominator as mentioned in stability of the numerical solutions of differential equations.
  | 2 | 3 | 1 | | | 0 | | = | | 1 | | ∴ | Y(s)= | s+1 s2+3s+2 | = | 1 s+2 | (3.51) |
| 3 | 1 | 0 | 1 | 1 | |||||||||||||
| 1 | 0 | 0 | −2 | 0 |
. . When the differential equation is z" +20z' +2z=0 with z(0)=1 and z' (0)=0, the Laplace transform of y(t)=z(t)u(t) is expressed in Eq.(3.52) because of k=0 and the numerical simulator is able to obtain the exact result up to large t.
| 2 | 20 | 1 | | | 0 | | = | | 20 | | ∴ | Y(s)= | s+20 s2+20s+2 | (3.52) |
| 20 | 1 | 0 | 1 | 1 | |||||||||||
| 1 | 0 | 0 | 0 | 0 |
. . These examples show that the numerical simulator is not able to obtain the exact result up to large t, when the constant in numerator is not larger than the factor of s. However the cause is not due to the numerical simulator but due to the impulsive response of rounded errors. Inverse Laplace transformation also is not able to obtain the exact result up to large t in case that the zeros and poles are not integer so the cancellation in Eq.(3.51) is not possible by the rounded errors.
. . The numerical calculus does not satisfy the associative law of addition in such case as (π×10−9+π)−π, where the result is zero and not π×10−9 in single precision. There are many cases where it very affects the accuracy of numerical results as the trouble of a quadratic equation. However the value π×10−9 should be considered as zero in order to satisfy the associative law of addition. Hence if the numerical results of differential equation decreases to such value, it should be considered as zero.
. . If it is considered as significant value, it means that only the value is amplified by 109, which the floating decimal point system shows as the reciprocal. The automatic control systems must not vary the amplified ratio according to the magnitude of input or output data varying with time.
. . It is said that the digital systems have better accuracy than the analog systems. It means that the digital systems be able to have the accuracy of many significant figures as 7, 16, ……, whereas the analog systems almost have the accuracy of three significant figures. It does not mean that the amplified ratio is variable.
3.9 The convolution integral.
. .
The convolution integral is expressed in Eq.(3.53) and has the variable t at the two positions which are the integrand and upper limit of integration. Hence the derivative with respect t is equal to the sum of two derivatives assuming that either variable t is constant as mentioned in Theorem 3.5. Hence it is expressed in Eq.(3.54).
 | t | f(τ)g(t−τ)dτ = | | t | f(t−τ)g(τ)dτ | (3.53) |
| 0 | 0 |
| d dt | | t | f(τ)g(t−τ)dτ=f(t)g(0)+ | | t | f(τ) | d dt | g(t−τ)dτ | (3.54) |
| 0 | 0 |
| d dt | | t | g(t, τ)dτ=g(t, t)+ | | t | d dt | g(t, τ)dτ | (3.55) |
| 0 | 0 |
| [Q.E.D.] |
. . The convolution integral is defined over all the range of t so the Laplace transform must rigorously be obtained by multiplying it by u(t) as shown in Theorem 3.6, although the result is not affected by u(t) because the convolution integral is zero for t=0. Hence, the inverse transform L−1F(s)G(s) is the convolution integral multiplied by u(t).
. .
[Theorem 3.6]. .When f(t) and g(t) are the solutions of two homogeneous differential equations, the product of these Laplace transforms are
| F(s)•G(s)= | | ∞ | e | −st | u(t) | | t | f(τ)g(t−τ)dτdt | (3.56) |
| 0 | 0 |
| [Proof] | G(s)= | | ∞ | g(t)u(t)e | −st | dt = | | ∞ | g(t−τ)u(t−τ)e | −s(t−τ) | dt |
| 0 | τ |
| F(s)•G(s)= | | ∞ | f(τ)u(τ)e | −sτ | dτG(s)= | | ∞ | f(τ)u(τ)e | −sτ | | ∞ | g(t)u(t)e | −st | dtdτ |
| 0 | 0 | 0 |
| = | ∞ | | ∞ | f(τ)u(τ)g(t−τ)u(t−τ)e | −st | dtdτ | |
| 0 | τ |
| F(s)•G(s)= | | ∞ | | t | f(τ)u(τ)g(t−τ)u(t−τ)e | −st | dτdt= | | ∞ | e | −st | u(t) | | t | f(τ)g(t−τ)dτdt |
| 0 | 0 | 0 | 0 |
| [Q.E.D.]__________ |
. . If h(t) is the impulsive response of a transfer function G(s), it is already mentioned that h(t)=L−1{G(s)×1}=kδ(t)+g(t)u(t), where g(t) is the solution of the homogeneous differential equation with the initial values by Theorem 3.4. The impulsive response also is expressed in h(t)=L−1G(s) so it must be satisfied that δ(t) has no effect on the convolution integral with h(t).
| . .[Theorem 3.7] | | t | δ(τ)δ(t−τ)dτ=δ(t) | (3.57) |
| 0 |
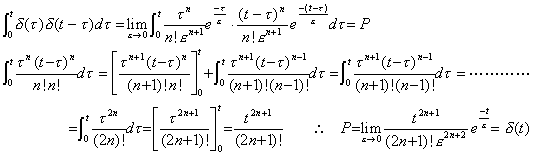[Q.E.D.]| . .[Theorem 3.8] | | t | h(τ)δ(t−τ)dτ=h(t), . .where. . h(t)=kδ(t)+g(t)u(t) | (3.58) |
| 0 |
| t | {kδ(τ)+g(τ)u(τ)}δ(t−τ)dτ= kδ(t)+g(t)u(t) | | t | δ(t−τ)dτ= kδ(t)+g(t)u(t) |
| 0 | 0 | [Q.E.D.] |
. . [Theorem 3.9]. .Denoting the Laplace transform of kfδ(t)+f(t)u(t) and h(t)=khδ(t)+g(t)u(t) as F(s) and G(s) respectively,
| ∞ | e | −st | | t | h(τ){k | f | δ(t−τ)+f(t−τ)u(t−τ)}dτdt= G(s)•F(s) | (3.59) |
| 0 | 0 |
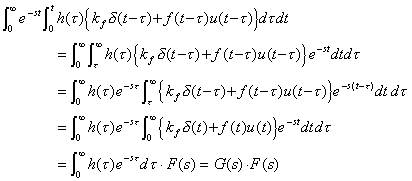[Q.E.D.]. .
By above theorems, if the convolution integral of h(t) and δ(t) is zero, the function h(t) is always zero for any t. Therefore if the Laplace transform H(s)×1 is zero, H(s) is zero, that is, the function h(t) is always zero for any t. It is the same with the convolution integral of any two functions.
. .
The impulsive response h(t) has zero for t≤0 so the Laplace transformation does not need to multiply the convolution integral by u(t). In case of kf=kh=0, Theorem 3.9 is equivalent to Theorem 3.6 and it does not need to multiply the convolution integral by u(t) because of h(t)=g(t)u(t).
. .
The Laplace transformable function except of δ(t) or its derivatives has the Laplace transform with the numerator of lower degree than the denominator. Hence if Y(s) is the response of the transfer function G(s) excited by such a function F(s), the exciting function is f(t)u(t) and the response y(t) is expressed in the convolution integral of h(t) and f(t). Therefore it is represented in y(t)=z(t)u(t) as follows.
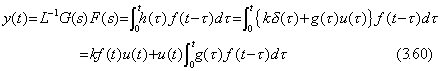
3.10 The differential equation and the transfer function with any excitation.
. .
When Y(s) is the response of a transfer function G(s) excited by F(s), it is expressed in Eq.(3.61). The values of f(t)u(t) and all derivatives are zero for t=0 from the proof of Theorem 3.3. The values of y(t) and all derivatives also are zero for t=0, because of y(t)=z(t)u(t) by Eq.(3.60). Hence y(t) is the solution of the differential equation Eq.(3.62) by Theorem 3.3.
| Y(s)= G(s)F(s)= | bnsn+bn−1sn−1+bn−2sn−2+  +b0sn+an−1sn−1+an−2sn−2+ +a0 | F(s) | (3.61) |
| y(n)+an−1y(n−1)+an−2y(n−2)+ +a0y= bn{f •u}(n)+bn−1{f•u}(n−1)+ +b0{f•u} | (3.62) |
| z(t)= kf(t)+ | | t | g(τ)f(t−τ)dτ | (3.63) |
| 0 |
. . [Theorem 3.10]. .z(t) is the solution of following differential equation.
| z(n)+an−1z(n−1)+an−2z(n−2)+ +a0z= bnf(n)+bn−1f(n−1)+ +b0f | (3.64) | ||||||||||||||||||||||||||||||||||||||||||||||
| (3.65) |
 ___.   |
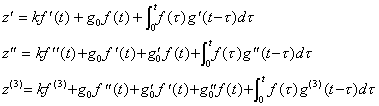. . The impulsive response of the transfer function G(s) is
|
h(n)+an−1h(n−1)+ +a0h= bnδ(n)+bn−1δ(n−1)+ +b0δ |
| g(n)+an−1g(n−1)+ +a0g=0. |
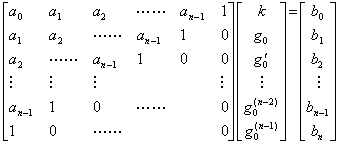
. . The initial values in Eq.(3.65) are obtained by substituting t=0 into z(t) and its derivatives.
| [Q.E.D.] |
| . . [Theorem 3.11]. .Eq.(3.65) is equivalent to | AZ=FTB | (3.66) |
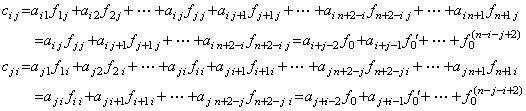
Hence cij=cji, that is, (AF)T=AF. The matrix A is also symmetrical and AT=A. Therefore,
| AZ=AFG=AFA−1B=FTATA−1B=FTB | [Q.E.D.] |
. . It is easily shown that y(t)=z(t)u(t) satisfies the differential equation in Eq.(3.62) because all the derivatives of y(t) and
 | ||
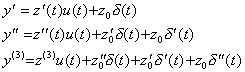| (3.67) | |
 | ||
 | ||
| ||
 | ||
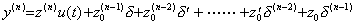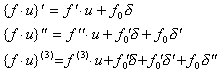| . .Example 1.. .Y(s)= | s−a s+a | • | 1 s2 | . .is equivalent to | . .y' +ay={tu(t)}' −atu(t). .with y(0)=0 | (3.68) |
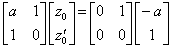, . .that is, z0=0.
| The general solution is . .z= | 2 a | −t+C | e | −at | . .and the constant is . .C= | −2 a | . .by z(0)=0. |
. .
Example 2.. .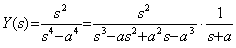
is equivalent to
.
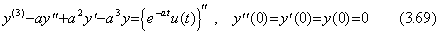
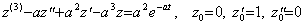
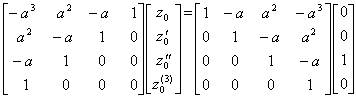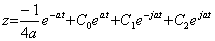and the constants are,
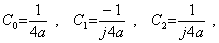. .therefore 
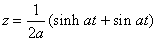.. . The numerical results are easily obtained by solving the differential equation in Eq.(3.64) with the initial values in Eq.(3.66) by use of the numerical solution of differential equations. It does not use any pole so it does not need the calculation of complex numbers.
3.11 Simplified method.
. .
In case that it is difficult to differentiate the function f(t), the right side of the differential equation in Eq.(3.64) may be obtained by the method of numerical differentiation. However, it may have some problem as to the precision. The problem is avoidable by the following theorem.
. .
[Theorem 3.12]. . The differential equation in Eq.(3.62) is equivalent to
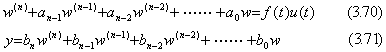
[Proof]. .By differentiating Eq.(3.70),
 |
|
 |
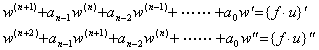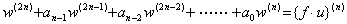| [Q.E.D.]__________ |
. . The solution of Eq.(3.70) is w=z(t)u(t) and z(t) is the solution of the differential equation in Eq.(3.72) with all the initial values of zero by Theorem 3.10 and 3.11. The solution y(t) in Eq.(3.71) is obtained by Eq.(3.73), because all the derivatives are w(k)=z(k)(t)u(t), which are easily shown by Eqs.(3.67) with all the initial values of zero.
. .
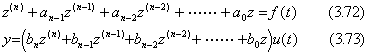
In case of above Example 1, Eq.(3.72) comes to z' +az=t, z(0)=0. The solution is
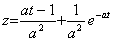. . .Hence, 
.. .
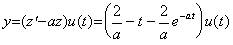In case of above Example 2, Eq.(3.72) comes to
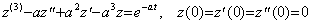.The solution is
.. .
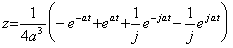
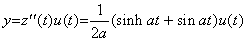In case of numerical solution, all the derivatives z(n−1) to z' are obtained by the sequential integral of z(n) during the process solving the differential equation. Therefore this numerical method is very simple and easy because of no need for calculating the initial values and the derivatives of f(t).
. .
The transfer function G(s) in Eq.(3.61) may be expressed in the product of two transfer functions G1(s), G2(s) expressed in as follows.
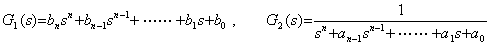
. . The method solving the differential equation Eq.(3.62) is equivalent to the method obtaining the response of G2(s) excited by G1(s)F(s) and the method solving by Theorem 3.12 is equivalent to the method obtaining the response of G1(s) excited by G2(s)F(s). Hence the one and the other come to the same thing. However, the other is favourable in case of numerical solution.
. . The impulsive response of transfer function is the solution of the differential equation substituted δ(t) for f(t)u(t) in Eq.(3.62). Hence the differential equation is transformed as follows.
. .
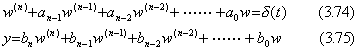
Eq.(3.74) is equivalent to Eq.(3.76) by Theorem 3.4 and Eq.(3.75) is equivalent to Eq.(3.77) because,
. .
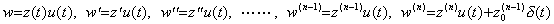
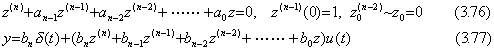
In case of bn≠0, δ(t) in the solution Eq.(3.77) is the function exciting the differential equation in Eq.(3.74) and the second term is the solution of the differential equation in Eq.(3.76). Hence the numerical solution also obtains only the second term.
. .
In case of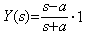 
, the solution of z' +az=0, z(0)=1 is z=e−at. Therefore,
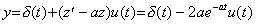
. . In case of a system of differential equation in Eq.(3.78), which is called a stiff differential equation, it may be solved by Laplace transform as in Eqs.(3.79). The solutions y1 and y2 are expressed in Eqs.(3.82), where z(t) is the solution of the differential equation in Eq.(3.80) and expressed in Eq.(3.81).
. .
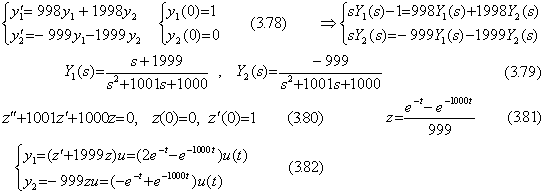
In case of numerical method, the differential equation in Eq.(3.80) has the condition for existence of solution expressed in Eq.(3.83) as it is mentioned in Section 1.5. The condition comes to h<0.000998, where h is a half of step interval in case of the author's 3 points method and Runge-Kutta's method. The value h must satisfy more severe condition for obtaining accurate results around t=0, but the condition is not obtained before the solution is obtained. The problem is solved by the author's variable pitch method mentioned in Section 2.3.
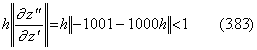
3.12 The program of the numerical simulator.
. .
The program of the numerical simulator is of the same as Program 2.2 which is the solution of n-th order differential equations, except of the printing routine which requires the subroutine for calculating the numerator of the transfer function as follows.
|
54 IF EB<EE THEN RETURN ELSE GOSUB 55:YY#=G:X#=X2:GOSUB 60:LOCATE 40,CSRLIN . . :PRINT USING"Y=##.#######^^^^ True=##.########^^^^";YY#;Y#:RETURN 55 G=Y(2)+1999*Y(1):RETURN 56 F=-1001*Y(2)-1000*Y(1):RETURN 58 XB=0:XE=50:N=500:ND=2:Y(1)=0:Y(2)=1:RETURN 60 Y#=2*EXP(-X#)-EXP(-1000*X#):RETURN [Note] Y(k+1)=z(k), ND=n-th order, N=the number of equidistances between XB to XE. |
. . "IF EB<EE THEN RETURN ELSE" is given at the head of Line 54 which is the subroutine printing the results, in order to print only the results at the equidistant points given by Line 58. "GOSUB 55:YY#=G" is also substituted for "YY#=Y(1)" in Line 54. Line 55 gives the value of the polynomial of Eq.(3.73) and Eq.(3.77), where Y(k+1) has the value of z(k). Line 56 gives the value z(n) of the differential equation in Eq.(3.72) as follows.
. .
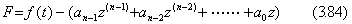
In case of indicial response, f(t) is one and in case of impulsive response, f(t) is zero. The initial values are all zero except that the (n−1)th derivative is one in case of impulsive response. These initial values must be given Line 58. Line 60 may be eliminated together with "GOSUB 60" and the variable Y# with the format in Line 54, if it is not the purpose to test the accuracy of the results.
. .
Above subroutines simulate the impulsive response of the transfer function Y1(s) in Eqs.(3.79). The following table represents the results. The value EE represents that the last integral interval is 0.1÷EE in every step. It comes to about 4000 around t=0 in the first step interval [0, 0.1].
| Table 3.3 Impulsive response of Y1(s). | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IB | EE | t | y1 | Accurate | exp | IB | EE | t | y1 | Accurate | exp | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
64 64 64 64 64 64 128 64 64 64 64 64 32 64 64 32 64 32 32 32 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
1.8096750 1.6374615 1.4816363 1.3406391 1.2130605 1.0976226 9.9317008 8.9865738 8.1313872 7.3575842 6.6574168 6.0238808 5.4506326 4.9319360 4.4625986 4.0379262 3.6536667 3.3059734 2.9913682 2.7067021 |
1.80967483 1.63746150 1.48163642 1.34064008 1.21306132 1.09762325 9.93170619 8.98657918 8.13139290 7.35758882 6.65742152 6.02388395 5.45063547 4.93193940 4.46260320 4.03793026 3.65367031 3.30597753 2.99137246 2.70670566 |
00 00 00 00 00 00 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 |
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
32 64 64 64 128 64 64 32 32 32 32 32 128 128 64 64 128 32 64 64 |
2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4.0 |
2.4491251 2.2160603 2.0051749 1.8143575 1.6416985 1.4854699 1.3441086 1.2162002 1.1004636 9.9574067 9.0098321 8.1524305 7.3766239 6.6746421 6.0394671 5.4647338 4.9446959 4.4741459 4.0483732 3.6631193 |
2.44912821 2.21606306 2.00517697 1.81435889 1.64169997 1.48547135 1.34411019 1.21620131 1.10046430 9.95741367 9.00983919 8.15244041 7.37663383 6.67465336 6.03947668 5.46474371 4.94470506 4.47415458 4.04838190 3.66312778 |
-01 -01 -01 -01 -01 -01 -01 -01 -01 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 | |
3.13 The most important idea.
. . Above mentioned methods show that the method solving a problem is not only one. If we would like to obtain the response in expression of function, the inverse Laplace transformation is simple and favorable. However, if we would like to obtain the response in expression of numerical data, the numerical solution of n-th order differential equations is simple and favorable because it does not need to compute poles and use complex numbers.
. . The analog computer simulates a higher order transfer function by combination of first order and second order transfer functions. It is equivalent to the simulation of inverse Laplace transformation, that is, the simulation of integral system. The digital computer is also able to simulate it in the similar way. However, it is simpler and better to simulate it by the author's numerical solution of n-th order differential equations because of no need of any language for simulation. It is the simulation of the differential equation and it is able to simulate such a system that the differential equation is not expressed in Laplace transform.
. . These show that there may be some simpler and better method solving a problem in case of digital system, even if it is not simple in case of analog system. It is the same with the simulation of the brain, which the author considers as automatic controller. This idea comes to develop the new simple method for synthesis and recognition of voice and for hyper-parallel processing.