4.2　閉ループ系の数値解法
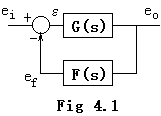Fig4.1. . 自動制御システムは通常、出力が入力にフィードバックされた閉ループ系である。そのブロックダイアグラムは Fig 4.1 のように図示される。一般に、伝達関数 G(s)及び F(s)はそれぞれ(4.3)及び(4.4)の形をとる。入出力の関係は閉ループ伝達関数を用いて(4.5)で表される。従って、その関係は第３節で述べた伝達関数を微分方程式に変換する数値シミュレータによりシミュレートできる。

Eq4_3
Eq4_4
Eq4_5
. . しかし、伝達関数 G(s)及び F(s)のそれぞれを変換した２つの微分方程式の連立方程式として解く方がより簡単である。何故なら、全ての値 eo, ef, ε が同時に得られ、閉ループ伝達関数を求める必要がないからである。その微分方程式は(4.6)になり、全ての信号は ei=ei(t)u(t), eo=eo(t)u(t) 及び ef=ef(t)u(t)であるから初期値は全て零である。
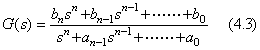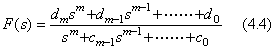. . この連立微分方程式を解くために、ユニットステップ関数は微分方程式の形を何ら変えることなく取り除いてよい。しかし、第 3.6 節に述べたように、初期値は伝達関数の分子、分母の補助変数 s の係数によって決定される値に替えなければならず、解には u(t)を掛けなければならない。
Eq4_6
. . ユニットステップ関数を全て取り除いたとき、eo(t), ef(t)及びこれらの導関数の初期値は次の行列の式で決められる。但し、簡単のために、ei, eo, ef及びこれらの微分表現は初期値を表している。
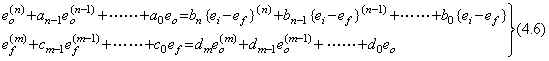
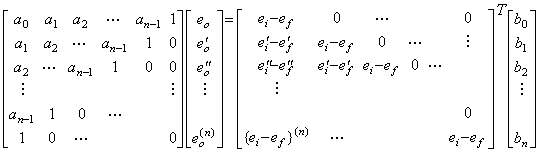
Eq4_6a
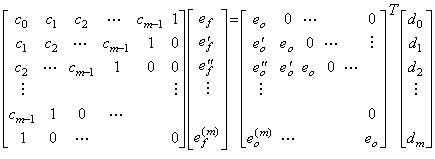
Eq4_6b
. . これら初期値の計算を省くために、これらの伝達関数は Fig 4.2 に示すように、分子と分母の二つの部分に分割できる。開ループ系及び閉ループ伝達関数の場合は、第 3.11 節で述べたように、出力 eoは微分方程式の数値解法の１ステップ区間の端の点だけの解 e 及び微係数の和として求めてよい。
Fig4_2
. . しかし、閉ループ系の場合は、伝達関数の分子の結果は微分方程式の数値解法の１ステップで使用される全ての点で計算されなければならない。従って、４変数 e, eo, f, ef の連立微分方程式となる。しかし、第３節で述べた数値シミュレータ、及び、連立微分方程式の数値解法 Program 4.1 を利用するには eoと ef は出力として１ステップの端の点でのみ計算し、２変数 e, f の連立微分方程式とする方が簡単である。従って、(4.7)に示すように、フォーワド伝達関数の分子はフィードバック伝達関数の微分方程式を駆動する関数に記述しなければならず、フィードバック伝達関数の分子はフォーワド伝達関数の微分方程式に記述しなければならない。
Eq4_7
. . 記号 e 及び f も e=e(t)u(t) 及び f=f(t)u(t)であり、ユニットステップ関数は微分方程式及び初期値に何の変更も加えることなく取り除くことができる。その場合、連立微分方程式(4.7)の初期値はインパルス応答の場合以外は全て零である。ユニットステップ応答は ei=1 且つ、初期値は全て零である。インパルス応答の場合は ei=0 であり、初期値はインパルス関数 δ(t)に等価な e(n−1)=1 である。この場合、係数 bnの値が零でないなら、f(m−1)の初期値は bnの値でなければならない。何故なら、フィードバック回路の微分方程式は、第3.6節に述べたように、フォワード回路の同次微分方程式の解に追加されるインパルス関数 bnδ(t)を持つ出力 eoに駆動されるからである。更に、係数 dmの値も零でないなら、フィードバック信号 efはインパルス関数 dmbnδ(t)が追加され、フォワード回路の微分方程式は入力インパルスとフィードバックインパルスの差により駆動される。従って、その結果は以下のようになる。
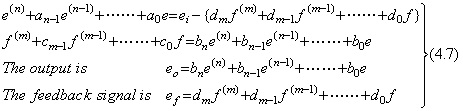
. . 出力を eo=kδ+…… とすれば、フィードバック信号は ef=dmkδ+…… である。従って、
Eq4_8

この結果は次のように閉ループ伝達関数から得ることもできる。
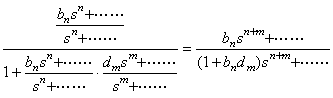
Eq4_8a
この結果はフォワード回路及びフィードバック回路の微分方程式はそれぞれ次のインパルス関数に駆動されることになる。
Eq4_9 Eq4_10
. . 従って、(4.7)において bn≠0 且つ dm≠0 の場合は、インパルス応答の微分方程式は(4.11)の初期値を持つ同次微分方程式となる。そして解 eo 及び efは、k を(4.8)の値として、それぞれ kδ 及び dmkδ を加えなければならない。
Eq4_11
. . bn≠0 且つ dm≠0 の例として、G(s) 及び F(s)を次に示す一次の伝達関数とする。
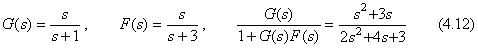
Eq4_12
インパルス応答は次のようになる。
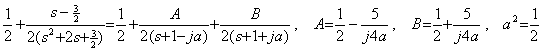
Eq4_12a
従って、
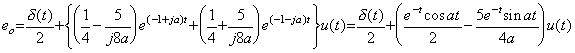Eq4_13. .(4.13)
フィードバック信号は次のようになる。
Eq4_13a
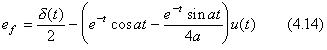
Eq4_14
. . 上記の閉ループ系は(4.6)により次に示すように二つの微分方程式よりなる連立微分方程式に表される。
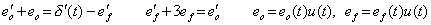Eq4_15_____(4.15)
第１式より ef' 及び efを消去すると、
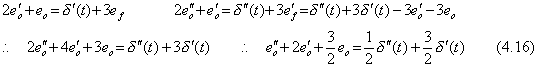
Eq4_16
第 3.6 節の(3.38)により右辺の関数を初期値に変換すると、次のように同次微分方程式が得られる。
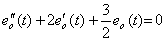Eq4_17_________(4.17)
初期値は次のように得られる。
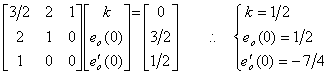Eq4_18______(4.18)
故に、解は次のようになる。
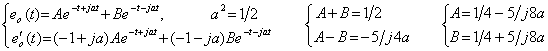
Eq4_18a
eo(t)に u(t) を掛け、 kδ(t)= δ(t)/2 を加えれば(4.13)と同じ結果になる。
. . 同次微分方程式(4.17)の初期値の計算を省略するためには、微分方程式(4.16)を次のように変換する。
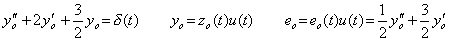Eq4_19___(4.19)
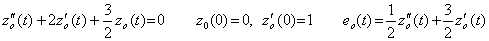u(t) 及び δ(t)を取り除くと、これは(4.20)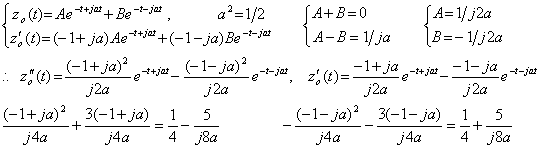に等価である。
Eq4_20___(4.20)
この解は次の計算結果により上記の解と同じである。
Eq4_20a
同様に、(4.15)の第２式より eo' 及び eoを消去すれば(4.14)に示した結果が得られる。
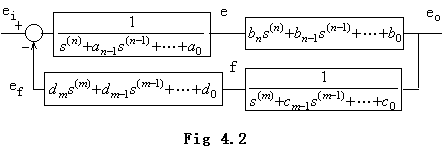
. . 初期値の計算を省くために、(4.12)の伝達関数 G(s)及び F(s)は Fig. 4.2 に示すように分子と分母の２つの部分に分けることが出来る。この場合、微分方程式(4.15)は次のように変換される。
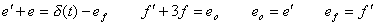Eq4_21____(4.21)
この４つの微分方程式の連立方程式は(4.7)に述べたように、 efに f ' を代入し、eoに e' を代入することにより２つの微分方程式の連立方程式に変わる。
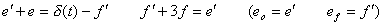Eq4_22____(4.22)
関数 e 及び f はそれぞれ e=e(t)u(t) 及び f=f(t)u(t)である。インパルス関数が存在しないなら、ユニットステップ関数は微分方程式の形を変えることなく取り除くことが出来、初期値は全て零である。しかし、インパルス関数が存在するので、それを初期値に変換しなければならない。ユニットステップ関数を取り除く前に関数 f ' 及び f を消去するなら、同次微分方程式(4.17)を解くことと同じである。関数 f ' 及び f を消去する前にユニットステップ関数を取り除くなら、インパルス関数が変換される初期値は１ではない。関数 ef は(4.10)によりインパルス関数 δ(t)/2 を持っている。それは明示されておらず、ef又は f ' が消去されたとき一緒に消去される。従って、インパルス関数は初期値１に変換される。関数 f ' 及び f を消去する前にユニットステップ関数を取り除く場合は、関数 efが持つ明示されていないインパルス関数を差し引かなければならない。同様に、関数 eoが持つ明示されていないインパルス関数はフィードバック回路の微分方程式を駆動する関数に加えなければならない。従って、初期値は(4.11)によりそれぞれ決定しなければならず、微分方程式(4.22)は次のように変換される。
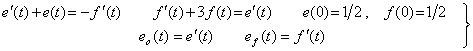Eq4_23____(4.23)
f ' (t) 及び f(t)を消去すると、
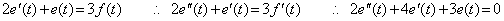
Eq4_23a
第１式に初期値を代入すると初期値 e' (0)=1/2 が得られる。従って、解は次のように得られる。
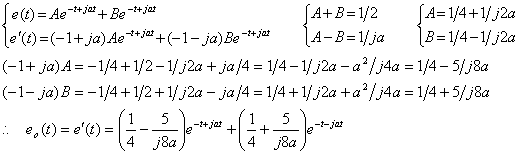
Eq4_23b
従って、eo=eo(t)u(t)+δ(t)/2 は(4.13)になる。同様に、e' (t) 及び e(t)を(4.23)から消去すれば(4.14)の解 ef が得られる。
. . 第 4.1 節で述べた連立微分方程式の数値解法により(4.7)を解くためには、各微分方程式の最高次微係数は低次微係数の式として表されなければならない。F1 及び F2をそれぞれ e(n) 及び f(m)の代わりに用いると、(4.7)は(4.25)で表せる。従って、F1 及び F2は連立方程式の解を与えられなければならず、それは(4.26)で表される。(4.26)は ei=δ(t)の場合には初期値は(4.11)になることも示している。
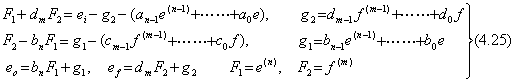
Eq4_25
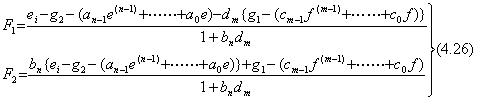
Eq4_26
. . フォワード回路及びフィードバック回路に多くの伝達関数がある場合には、それらの伝達関数はそれぞれ微分方程式に変換できる。それら微分方程式が多くの未知数 F1, F2, …… を持つ連立方程式を構成するときは、連立微分方程式を解くプログラムは連立方程式の解 F1, F2, …… を得る副プログラムを与えられれば良い。

4.3　閉ループ系の数値シミュレータ
. . 閉ループ系の数値解は連立微分方程式の解を得る Program 4.1 を用いて得ることが出来る。しかし、そのプログラムは Program 4.2 に太字で示したように少し変更されねばならない。何故なら、その連立微分方程式は(4.25)に示すように伝達関数の分子に等価な式が付加されているからである。
. . 第10行には配列 G(5) を追加しなければならない。それは(4.25)の g1 及び g2を G(1) 及び G(2)にそれぞれ代入するために使われる。変数 G(1) 及び G(2)はそれぞれ eo 及び efの値の計算にも使われる。第40行の"GOSUB 60"は"GOSUB 54"の後に置かれる。"GOSUB 54"はそのステップの解に対する g1, g2, F1 及び F2を次のステップの出発値として第62行を用いて計算する。第 60 行の先頭の"IF EB<EE THEN RETURN ELSE"は第 64 行に記述された点の解だけをプリントするために追加されている。第 60 行の変数 YY# は G(J)の値を代入されなければならない。
. . 第 66 行において、bn 及び dmの値の両者が零でないなら、eo 及び efの値は第 62 行で計算された値を用いて計算し、それぞれ G(1) 及び G(2)に代入しなければならない。bn 及び dmの値の両者が零なら、eo 及び efの値は第 66 行で計算する必要はない。何故なら、それらの値は第 62 行で計算された値と同じだからである。第 62 行には連立方程式(4.25)の解である(4.26)を与えればよい。
. . 例題(4.12)は連立微分方程式(4.22)を与えるから、 e' 及び f ' に関する連立方程式(4.27)を構成する。その解は(4.28)で表される。第 62 行は δ を含まないこれらの式をそれぞれ F(1) 及び F(2)に与えねばならない。解 e 及び f の値は主プログラムで Y(1,1) 及び Y(1,2)にそれぞれ与えられる。この場合は、g1 及び g2の値は共に零であるから G(1) 及び G(2)は第 62 行では使われない。

Eq4_27 Eq4_28
. . 第 64 行は積分範囲 XB から XE, 分割数 N, 微分方程式の数 NF, 各微分方程式の階数 ND(1) 及び ND(2), 初期値 Y(1,1)=e(0) 及び Y(1,2)=f(0)を与えなければならない。但し、(4.28)の両式とも δ/2 を持つから e(0) 及び f(0)は 1/2 である。
. . 第 66 行には、解の正確さを比較する必要があるなら正確な解の値を与える。eo=e' 及び ef=f ' の値は、この例題では(4.25)により G(1) 及び G(2)にそれぞれ与えられなければならない。
. . 例題の数値解 eo(t) 及び ef(t)を Table 4.2 に示す。伝達関数の与える真の解 eo=eo(t)u(t) 及び ef=ef(t)u(t)は t≤+0 において数値解を少し修正しなければならない。(4.21)(4.28)により、eo(0)=1/2 及び ef(0)=−1 であるが、eo=eo(0)u(0)=0, ef=ef(0)u(0)=0 であり、eo=eo(+0)u(+0)=1/2, ef=ef(+0)u(+0)=−1 である。更に、インパルス関数 δ(t)/2 を重畳しなければならない。

Program 4.2 The simulator of closed-loop systems.
(The other lines are of the same as Program 4.1.)

10 DIM Y0(6,5),Y1(6,5),Y2(6,5),Y(6,5),F(5),G(5),R1(5),R2(5),R3(5),RA(5),ND(5),
. . Y#(5):DEFINT E,J,N
40 GOSUB 44:IF J>NF THEN X=X2:GOSUB 54:GOSUB 60:X0=X2:GOSUB 46 ELSE
. . IF EE<&H4000 THEN EE=EE*2:ES=EB*2-1:EB=EE+1 ELSE PRINT"EE>&h4000":END
60 IF EB<EE THEN RETURN ELSE X#=X2:GOSUB 66:FOR J=1 TO NF:YY#=G(J):PRINT USING
. . " Y(#)=##.#######^^^^ True=##.########^^^^";J;YY#;Y#(J);:NEXT:PRINT:RETURN

62 F(1)=(3*Y(1,2)-Y(1,1))*.5:F(2)=(-3*Y(1,2)-Y(1,1))*.5:RETURN
64 XB=0:XE=50:N=500:NF=2:ND(1)=1:Y(1,1)=.5:ND(2)=1:Y(1,2)=.5:RETURN
66 G(1)=F(1):G(2)=F(2):A#=SQR(.5#):AS#=A#*X#:AC#=COS(AS#):AS#=SIN(AS#)/A#:
. . A#=EXP(-X#):Y#(1)=A#*(.5*AC#-1.25*AS#):Y#(2)=-A#*(AC#-.25*AS#):RETURN

Table 4.2 The results of impulsive response in Eqs.(4.12).
IBEBEEteo(t)Accurateexpef(t)Accurateexp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
32
34
36
38
40
42
44
46
48
50
52
56
60
64
68
72
76
80
84
88
92
96
100		 2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2		 2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2		 0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.2
3.4
3.6
3.8
4.0
4.2
4.4
4.6
4.8
5.0
5.2
5.6
6.0
6.4
6.8
7.2
7.6
8.0
8.4
8.8
9.2
9.6
10.0		 3.3827767
2.0127741
8.6378098
-8.8663399
-8.6725518
-1.4929368
-1.9849297
-2.3607880
-2.6364592
-2.8263611
-2.9434630
-2.9993707
-3.0044180
-2.9677558
-2.8974423
-2.8005326
-2.6831633
-2.5506365
-2.4075003
-2.2576204
-2.1042544
-1.9501172
-1.7974414
-1.6480346
-1.5033334
-1.3644494
-1.2322141
-1.1072179
-9.8984525
-8.8030852
-6.8489045
-5.2019704
-3.8420301
-2.7413853
-1.8687081
-1.1917829
-6.7938468
-3.0248410
-3.4955447
1.4609389
2.6026650
3.5076598
3.3462073
2.7317170
2.0131853
1.3642770
8.5174863
4.8350703
2.3973739
9.1377551
9.9158351
-2.8293309
-4.0879415		 3.38277684
2.01277443
8.63781348
-8.86630893
-8.67254764
-1.49293611
-1.98492897
-2.36078709
-2.63645837
-2.82636041
-2.94346219
-2.99937002
-3.00441736
-2.96775518
-2.89744186
-2.80053206
-2.68316278
-2.55063636
-2.40749996
-2.25762009
-2.10425417
-1.95011708
-1.79744121
-1.64803440
-1.50333339
-1.36444932
-1.23221416
-1.10721790
-9.89845314
-8.80308671
-6.84890494
-5.20197130
-3.84203108
-2.74138653
-1.86870912
-1.19178379
-6.79385556
-3.02484909
-3.49562163
1.46093238
2.60265935
3.50765597
3.34620512
2.73171595
2.01318500
1.36427691
8.51748748
4.83507218
2.39737582
9.13777214
9.91596499
-2.82932109
-4.08793504		 -01
-01
-02
-03
-02
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-02
-02
-02
-02
-02
-02
-02
-02
-03
-03
-04
-03
-03
-03
-03
-03
-03
-03
-04
-04
-04
-05
-06
-05
-05		 -8.7997419
-7.6975685
-6.6906661
-5.7754374
-4.9476907
-4.2028081
-3.5358837
-2.9418409
-2.4155346
-1.9518331
-1.5456839
-1.1921692
-8.8654846
-6.2428981
-4.0109359
-2.1290988
-5.5947155
7.3322579
1.7816417
2.6158214
3.2632709
3.7490472
4.0958643
4.3241985
4.4524271
4.4969566
4.4723529
4.3914836
4.2656440
4.1046955
3.7104812
3.2636534
2.8035451
2.3571745
1.9419763
1.5681034
1.2403297
9.5958496
7.2417832
5.3074714
3.7497010
1.5733159
3.4059049
-2.6846980
-4.9865741
-5.2132580
-4.4707864
-3.4130926
-2.3850615
-1.5368591
-9.0683068
-4.7687146
-2.0644571		 -8.79974176
-7.69756860
-6.69066619
-5.77543702
-4.94769060
-4.20280812
-3.53588365
-2.94184073
-2.41553457
-1.95183314
-1.54568386
-1.19216933
-8.86548581
-6.24290020
-4.01093853
-2.12910154
-5.59474373
7.33224267
1.78163935
2.61581861
3.26326929
3.74904643
4.09586191
4.32419647
4.45242569
4.49695504
4.47235189
4.39148207
4.26564271
4.10469461
3.71048003
3.26365261
2.80354428
2.35717406
1.94197594
1.56810324
1.24032965
9.59584942
7.24178414
5.30747275
3.74970282
1.57331748
3.40591884
-2.68468902
-4.98656819
-5.21325444
-4.47078409
-3.41309132
-2.38506089
-1.53685893
-9.06830829
-4.76871712
-2.06446008		 -01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-02
-02
-02
-02
-03
-03
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-03
-03
-03
-03
-03
-04
-04
-04
-04
-04
-04
-04
-04
-05
-05
-05

目　次　へ