4.　ｎ 階の連立微分方程式

4.1　n 階の連立微分方程式の数値解法
. . 通常、n 階の微分方程式は n 個の 1 階の微分方程式の連立方程式に置き換えて解かれる。従って、m 個の n 階の微分方程式の連立方程式は m×n 個の 1 階の微分方程式の連立方程式に置き換えられる。著者の解法は n 階の微分方程式を置き換えをすることなく解くことが出来る。従って、m 個の n 階の微分方程式の連立方程式も何ら置き換えをすることなく解くことが出来る。
. . n 階の連立微分方程式は(4.1)で表される。 n の値は n1 から nmであることが可能であり、駆動関数もそれそれに z1(t) から zm(t)であることが可能である。初期値として t=t0において y1(t) から ym(t)迄、及び、これらの n−1 次迄の微係数が与えられるなら、y1(n1)(t0) から ym(nm)(t0)迄の値が(4.1)により求まる。これらの値のそれぞれをEuler法により逐次に積分すれば、yk(nk−1)(t0+h) から yk(t0+h), (k=1∼m)が予測される。そして y1(n1)(t0+h) から ym(nm)(t0+h)が(4.1)により予測される。これらは著者の３点法の中点の予測値である。同様にして、著者の３点法により、中点の値は修正され、t0+2h の値が予測され、修正される。(4.1)の２番目からｍ番目迄の式で得られる値は最初の式の右辺の f1(t)を計算するためのパラメータである。従って、最初の式が解くべき n1階の微分方程式であり、その他は右辺の f1の一部である。故に、連立微分方程式(4.1)はこれらのパラメータを計算する手続きを付け加えれば前節で述べた方法により解くことができる。

Eq4_1

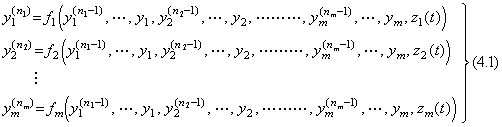
. . このプログラムは Program 4.1 に３点を用いる可変区分幅解法で示されている。解 y1 から ymはそれぞれ Y(1,1) から Y(1,m)の値であり、それらの n 次の微係数 y1(n) から ym(n)は Y(n+1,1) から Y(n+1,m)の値である。n 及び m の最大値はこのプログラムでは５であるが、もし必要なら、これらの値は配列の大きさを書き換えるだけで変更できる。
. . 常に、最初の微分方程式が解の存在に関する最悪の条件を持つなら、全ての解 y1 から ymは解 y1が収束したとき収束する。しかし、最悪の条件を予め評価することが常に容易であるとは限らない。この評価を省くために、Program 4.1 は全ての解 y1 から ymが収束したことを検出している。
. . 64 行の副プログラムは微分方程式の全数を NF に与え、微分方程式の階数をそれぞれ ND(1)∼ND(NF)に与えなければならない。又、y1∼y1(n−1) から ym∼ym(n−1)の初期値を Y(1,1)∼Y(n,1) から Y(1,m)∼Y(n,m)に与えなければならない。62 行の副プログラムは微分方程式を(4.1)に示された形式で F(1)∼F(NF)に与えなければならない。66 行は、必要があるなら正確な解を Y#(1)∼Y#(NF)に与える。
Program 4.1 The systems of n-th differential equations.
10 DIM Y0(6,5),Y1(6,5),Y2(6,5),Y(6,5),F(5),R1(5),R2(5),R3(5),RA(5),ND(5),Y#(5):
. . DEFINT E,J,N
12 DEF FNY1=(5*Y0(J3+1,J)+8*Y1(J3+1,J)-Y2(J3+1,J))*H3+Y0(J3,J):
. . DEF FNY2=(Y0(J3+1,J)+4*Y1(J3+1,J)+Y2(J3+1,J))*H4+Y0(J3,J)
14 RP=16777216#:RM=2/RP
16 GOSUB 64:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE;" N=";N;" H=";H0
18 EE=1:XL=XB:X=XB:GOSUB 54:FOR IB=1 TO N:ES=1:XI=XL:XL=XB+H0*IB:X0=XI
20 WHILE 2:H1=H0/EE:EB=ES:WHILE EB=<EE:X2=XI+H1*EB:IF EB=EE THEN X2=XL
22 LOCATE 0,CSRLIN:PRINT"IB=";IB;" EB=";EB;" EE=";EE;" X=";X2;:GOSUB 52
24 FOR J=1 TO NF:FOR J3=1 TO ND(J):Y1(J3,J)=Y0(J3+1,J)*H+Y0(J3,J):
. . Y(J3,J)=Y1(J3,J):NEXT J3,J:GOSUB 56
26 FOR J=1 TO NF:FOR J3=1 TO ND(J):Y1(J3,J)=(Y0(J3+1,J)+Y1(J3+1,J))*H*.5+
. . Y0(J3,J):Y2(J3,J)=Y1(J3+1,J)*H2+Y0(J3,J):Y(J3,J)=Y1(J3,J):NEXT J3,J:
. . GOSUB 56:GOSUB 58
28 FOR J=1 TO NF:IF ABS(Y2(ND(J),J))<1 THEN RA(J)=RP ELSE RA(J)=1
30 NEXT
32 FOR J=1 TO NF:FOR J3=1 TO ND(J):Y1(J3,J)=FNY1:Y2(J3,J)=FNY2:
. . Y(J3,J)=Y1(J3,J):NEXT J3,J:GOSUB 56:GOSUB 58
34 FOR J=1 TO NF:R1(J)=Y(ND(J),J)*RA(J):NEXT
36 FOR J=1 TO NF:FOR J3=ND(J) TO 1 STEP-1:Y1(J3,J)=FNY1:Y2(J3,J)=FNY2:
. . Y(J3,J)=Y1(J3,J):NEXT J3,J:GOSUB 56:GOSUB 58
38 FOR J=1 TO NF:J3=ND(J):R2(J)=Y(J3,J)*RA(J):Y2(J3,J)=FNY2:Y(J3,J)=Y2(J3,J):
. . R3(J)=Y(J3,J)*RA(J):RA(J)=RM*ABS(R3(J)):NEXT
40 GOSUB 44:IF J>NF THEN GOSUB 60:X=X2:GOSUB 54:X0=X2:GOSUB 46 ELSE
. . IF EE<&H4000 THEN EE=EE*2:ES=EB*2-1:EB=EE+1 ELSE PRINT"EE>&h4000":END
42 EB=EB+1:WEND:IF EB>EE+1 THEN WEND ELSE NEXT IB:END
44 FOR J=1 TO NF:IF ABS(R2(J)-R3(J))<RA(J) THEN NEXT:RETURN ELSE RETURN
46 GOSUB 50:IF J>NF THEN IF EE>1 AND(EB MOD 2=0)THEN EE=EE\2:ES=EB\2+1:
. . IF ES=<EE THEN EB=EE+1
48 RETURN
50 FOR J=1 TO NF:IF ABS(R1(J)-R3(J))<RA(J) THEN NEXT:RETURN ELSE RETURN
52 H2=X2-X0:H=H1*.5:H3=H/12:H4=H2/6:X1=X0+H:RETURN
54 GOSUB 62:FOR J=1 TO NF:Y0(ND(J)+1,J)=F(J):FOR J3=1 TO ND(J):
. . Y0(J3,J)=Y(J3,J):NEXT J3,J:RETURN
56 X=X1:GOSUB 62:FOR J=1 TO NF:Y1(ND(J)+1,J)=F(J):NEXT:RETURN
58 X=X2:FOR J=1 TO NF:FOR J3=1 TO ND(J):Y(J3,J)=Y2(J3,J):NEXT J3,J:GOSUB 62:
. . FOR J=1 TO NF:Y2(ND(J)+1,J)=F(J):NEXT:RETURN
60 X#=X2:GOSUB 66:FOR J=1 TO NF:YY#=Y(1,J):PRINT USING
. . " Y(#)=##.#######^^^^ True=##.########^^^^";J;YY#;Y#(J);:NEXT:PRINT:RETURN

62 F(1)=998*Y(1,1)+1998*Y(1,2):F(2)=-999*Y(1,1)-1999*Y(1,2):RETURN
64 XB=0:XE=50:N=500:NF=2:ND(1)=1:Y(1,1)=1:ND(2)=1:Y(1,2)=0:RETURN
66 Y#(1)=2*EXP(-X#)-EXP(-1000*X#):Y#(2)=EXP(-1000*X#)-EXP(-X#):RETURN
[Note] NF=the total number of differential equations, ND(k)=the order of
differential equation F(k), Y(n+1,k)=yk(n).


. . Program 4.1 には(4.2)に示された１階の硬い連立微分方程式を解く副プログラムが付いている。解の存在条件は(4.2)に等価な２階の微分方程式により得られ、h<0.000998 であることが既に示されている。t=0 の近傍で正確な結果を得るためには、その条件は前記に述べたように更に厳しいものとなる。１階の連立微分方程式でもそれは同じである。Table 4.1 は Program 4.1 による結果を示す。その最初のステップは 2048 に細分され、ステップ幅の半分は h=0.05/2048 になる。
Eq4_2

Table 4.1 The solution of Eqs.(4.2) with basic interval 2h=0.1.
IBEBEEt (exp)y1Accurateexpy2Accurateexp
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20		 1
20
11
40
21
36
19
26
14
18
10
11
32
32
96
64
128
128
128
128
64
128
128
128
128
128
128
128
64
128
64
64
32
64
128		 2048
2048
1024
1024
512
512
256
256
128
128
64
64
128
64
128
64
128
128
128
128
64
128
128
128
128
128
128
128
64
128
64
64
32
64
128		 4.88281(-5)
9.76562(-4)
1.07422(-3)
3.90625(-3)
4.10156(-3)
7.03125(-3)
7.42188(-3)
0.0101563
0.0109375
0.0140625
0.015625
0.0171875
0.025
0.05
0.075
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0		 1.0475576
1.6214446
1.6562884
1.9720868
1.9752667
1.9851029
1.9846131
1.9797512
1.9782262
1.9720711
1.9689929
1.9659190
1.9506201
1.9024584
1.8554869
1.8096740
1.6374605
1.4816362
1.3406390
1.2130588
1.0976230
9.9317253
8.9865988
8.1314176
7.3576128
6.6574448
6.0239094
5.4506582
4.9319580
4.4626218
4.0379471
3.6536843
3.3059886
2.9913905
2.7067178		 1.04755755
1.62144438
1.65628823
1.97208694
1.97526688
1.98510300
1.98461317
1.97975147
1.97822642
1.97207105
1.96899271
1.96591869
1.95061982
1.90245885
1.85548697
1.80967483
1.63746150
1.48163642
1.34064008
1.21306132
1.09762325
9.93170619
8.98657918
8.13139290
7.35758882
6.65742152
6.02388395
5.45063547
4.93193940
4.46260320
4.03793026
3.65367031
3.30597753
2.99137246
2.70670566		 +00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01		 -4.7606375
-6.2242049
-6.5736192
-9.7598553
-9.7935998
-9.9210954
-9.9200749
-9.8985618
-9.8910415
-9.8603511
-9.8449636
-9.8295945
-9.7531003
-9.5122916
-9.2774343
-9.0483701
-8.1873018
-7.4081802
-6.7031950
-6.0652941
-5.4881144
-4.9658629
-4.4932991
-4.0657088
-3.6788061
-3.3287224
-3.0119547
-2.7253291
-2.4659789
-2.2313108
-2.0189735
-1.8268421
-1.6529940
-1.4956951
-1.3533589		 -4.76063739
-6.22420463
-6.57361868
-9.75985575
-9.79360041
-9.92109585
-9.92007572
-9.89856317
-9.89104318
-9.86035133
-9.84496273
-9.82959328
-9.75309912
-9.51229424
-9.27743484
-9.04837417
-8.18730751
-7.40818212
-6.70320042
-6.06530660
-5.48811623
-4.96585310
-4.49328959
-4.06569645
-3.67879441
-3.32871076
-3.01194198
-2.72531774
-2.46596970
-2.23130160
-2.01896513
-1.82683515
-1.65298876
-1.49568623
-1.35335283		 -02
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01

目　次　へ