3. 伝達関数のインパルス応答を微分方程式で解く
3.1 はじめに
. .
著者は微分方程式の数値解法により伝達関数のインパルス応答を求めることを試みた。その理由は、高次システムの場合には逆ラプラス変換よりその方が簡単でよいと考えたからである。しかし、この試みは二つの問題を解決する必要があった。それらは数値計算の精度に関するものと、ラプラス変換された関数の t=0 における値に関するものである。それらの研究の結果は演算子法の発見とラプラス変換の厳密な定義の発見に至った。
. .
関数 f(t) の導関数のラプラス変換は(3.1)で表される。従って、インパルス関数の導関数についてもそれは同じであるべきである。しかし、ラプラス変換は
| L f ' (t)=sL f(t)−f(0) | (3.1) | L δ' (t)=sL δ(t)−δ(0) | (3.2) |
3.2 インパルス関数
. .
Dirac のデルタ関数は δ(0)が無限大であるから(3.2)を満足しない。インパルス関数は、
. .
[定義 1]. .
![]()
. .
インパルス関数は t=0 で上昇を開始して tp=nε でピークに達し、指数関数的に減衰する。その積分値は ε の値が何であっても常に1である。
| tp→+0, | δ(tp+0)→0, | δ(0)=0 | (3.5) |
| . . [定理 3.1] | f(+0)が f(0)に等しければ、 | f(t)δ(t)=f(0)δ(t), | (3.7) |
|
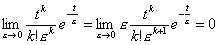
| for k=0, 1, 2, …… |
| ∴ f(t)δ(t)=f(0)δ(t) | [証明終] |
. .
δ(t−d)の場合には、インパルス関数は tp=d+0 にピークを持ち、t=tp以外の全ての点で零である。その積分値は1であり、次式の成立は明らかである。
| f(t)δ(t−d)=f(d)δ(t−d) | (3.8) |
| L δ(t−d)=e−sd | (3.9) |
3.3 ユニットステップ関数
. .
ユニットステップ関数はインパルス関数を
. .[定義 2]
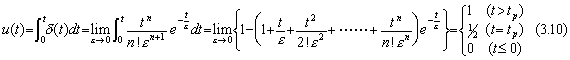
. .
定義により、ユニットステップ関数のラプラス変換は次のようになる。
. . その値は、次の関係があるからインパルス関数の積分値の半分であるとするのが良い。
|
| ∴ 2u(tp)δ(t)=δ(t) | ∴ 2u(tp)=1 |
| . . [定理 3.2] |
| __________={F(t)−F(d)}u(t−d) | [証明終] |
. .
f(t)に e−stを代入し、t→∞の極限をとれば u(t−d)のラプラス変換は、
| 故に、u(t−d)は u(t)と δ(t−d)の畳込み積分である。 |
3.4 任意関数のラプラス変換
. .
関数 f(t) が t>0 において既知であり、t≤0 で零であるとき、そのラプラス変換は次式で定義される。
. .
[定義 3]. .ラプラス変換は、t≤0 で常に零ではない関数 f(t) に u(t)e−at を掛けた結果のフーリエ変換である。即ち、
. .
定義により、ラプラス変換可能関数は厳密には f(t)u(t)と表されるべきである。ユニットステップ関数は(3.16)の積分に何の影響も与えないけれども、伝達関数を微分方程式で表すためには非常に重要である。何故なら、関数 f(t)に u(t)を掛けてあることが、ラプラス変換においては微分後の積分演算が可逆である理由だからである。原空間においても、 f(t)u(t)は微分後の積分が可逆である。何故なら、次に示すように
| sL f(t)u(t)=L f ' (t)u(t)+f(0) | (3.20) |
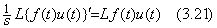
|
. . 初期値が与えられた微分方程式をラプラス変換するためには(3.20)を使用しなければならない。しかし、任意の伝達関数を微分方程式に変換するためには(3.21)を使用しなければならない。何故なら、f(t)及びその導関数の初期値が全て明示的に与えられていないからである。
| . .[定理 3.3] | L {f(t)u(t)}(n)=snL f(t)u(t) | (3.22) |
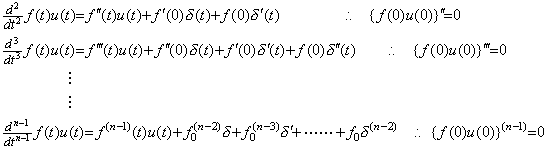
| L {f(t)u(t)}(n)=sL {f•u}(n−1)=s2L {f•u}(n−2)=……=snL {f•u} | [証明終] |
3.5 ラプラス変換とフーリエ変換
. .
(3.17)における関数 u(t)e−atは関数 f(t)の零から約 1/a 迄のtに対する部分を抽出する。従って、 a の値は正であること、及び、関数 f(t) が ebtの場合には、零から無限大までの積分の収束条件として b の値より大きいことを必要とする。故に、ラプラス変換は局所周波数応答を表す。
. .
t≤0 において常に零である関数 f(t) が t から t+d へシフトされたなら、そのラプラス変換は(3.23)で表される。これは、f(t−d)が f(t)と δ(t−d)の畳込み積分であることを示す。 a=0 の場合は、フーリエ変換が位相応答以外、シフト d の値により変わらないことを示す。一方、ラプラス変換の振幅応答は(3.16)の e−ad倍となる。
| f(t)u(t)=t2u(t)−(t−1)2u(t−1) |
位相応答は t=1 において重ね合わせがあることを示しているが、振幅応答 |F(jω)| は周波数特性が何処でも同じであることを示している。
. . 一方、s=a+jω 及び a »1 とすると、
|
| because of | (3.26) |
. . 周波数応答(3.26)は t<1 の範囲で意味を持ち、t≥1 の周波数応答は(3.24)により得られる。
. . 故に、フーリエ変換は二つの部分にある類似した特性を抽出するものであり、それが二つの関数の結合であることを理解するためには重ね合わせに関する高度な知識を必要とする抽出法である。一方、ラプラス変換は局所周波数応答であり、二つの部分にある異なった特性を抽出する。この応答は視覚に似ていると著者は考える。
. . ラプラス変換は、音声のように時間と共に変化する周波数応答を持つ現象の解析に対しても非常に有用である。しかし、結合の場所が明示されていればその解析は非常に簡単になる。音声はその場所を示すためにピッチ周期を持っていると著者は考える。
. . 通常は、フィルターは畳込み積分で表される技術により作用される。しかし、上記のフィルターはその技術によって作用させてはならない。何故なら、その場合のラプラス変換は(s+a)−1、即ち、低周波通過フィルターとなり、作用させた結果は短時間におけるより高い周波数に対して強い応答をする人間の感覚器官の結果とは非常に異なるからである。
3.6 インパルス応答とその微分方程式
. .
y(t)が(3.28)で表される伝達関数のインパルス応答であるとき、入力関数の t≤0 における値は全て零であるから出力 y(t)の t≤0 における値も全て零である。従って、出力 y(t)は、伝達関数が係数 bnを持つからそれが零でないなら(3.29)で表される。δ(0)から δ(n−1)(0)迄は δ(t)に関する定義1により全て零であり、y(0)から y(n−1)(0)迄は定理 3.3 の証明により全て零である。故に、(3.28)は定理 3.3 により(3.30)で表される微分方程式に変換される。
| Y(s)= | bnsn+bn−1sn−1+bn−2sn−2+………+b0 sn+an−1sn−1+an−2sn−2+………+a0 | •1 | (3.28) | y=z(t)u(t)+bnδ(t) | (3.29) |
| y(n)+an−1y(n−1)+an−2y(n−2)+………+a0y=bnδ(n)+bn−1δ(n−1)+bn−2δ(n−2)+………+b0δ | (3.30) |
. . この微分方程式は ε→0 にする前のインパルス関数の定義式を代入して微分方程式を解いた後 ε→0 にする方法で解析的に解くことができる。従来の δ(t)の定義ではこの方法は、右辺に b0δ(t)だけを持つ微分方程式の場合を除けば使用できない。
. . インパルス応答が(3.31)で表されるとき、初期値が
| Y(s)= | s+1999 s2+1001s+1000 | •1 | (3.31) | y" +1001y' +1000y=δ' (t)+1999δ(t) | (3.32) |
| δ' (t)+1999δ(t)= | 1 ε2 |
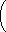 |
1− | t ε |
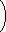 e e |
−t ε |
+ | 1999t ε2 | e | −t ε |
(3.33) |
y=Ae−t+Be−1000t+C1e | −t ε | +C2te |
−t ε |
A= | 2 (ε−1)2 | B= | −1 (1000ε−1)2 | (t≥0) | (3.34) | |||
| , | , | , |
C1= | −1999999ε2+3998ε−1 (1000ε−1)2(ε−1)2 | , | C2= | 1999ε−1 ε(1000ε−1)(ε−1) | (3.35) |
. . 特殊解は微分方程式を満足しなければならないから、定数 C1及び C2は(3.35)で表される。従って、定数 A 及び B は初期値 y(0)=y' (0)=0 により決定される。ε→0 にすると、これらの定数は A→2, B→−1, C1→−1, εC2→−1 となり、特殊解は t=0 では −1 に、t>0 では零に収束する。
. . 故に、解は t>0 では補関数に収束し、t≤0 では零に収束する。即ち、 z(t)を補関数とすれば、y=z(t)u(t)である。この解は Y(s) の逆ラプラス変換に同じである。従って、インパルス応答は右辺を零とした同次微分方程式を解くことにより得られる。但し、初期値は全てが零ではない。この同次微分方程式は次のようにあらわされる。
| z" +1001z' +1000z=0 | , | z(0)=1 | , | z' (0)=998 | (3.36) |
. .
[定理 3.4]. .
y(t)=z(t)u(t)+kδ(t)が微分方程式(3.30)の解であるとき、z(t)は同次微分方程式(3.37)で表され、その初期値は(3.38)で表される。
| z(n)+an−1z(n−1)+an−2z(n−2)+………+a0z=0 | (3.37) |
  | a0 | a1 | a2 |  | an−1 | 1 |   |   | k |   | = |   | b0 |   | (3.38) |
| a1 | a2 |  | an−1 | 1 | 0 | z0 | b1 | ||||||||
| a2 |  | an−1 | 1 | 0 | 0 | z0' | b2 | ||||||||
 |  |  |  | ||||||||||||
| an−1 | 1 | 0 |  | 0 | z0(n−2) | bn−1 | |||||||||
| 1 | 0 |  | 0 | z0(n−1) | bn |
| y(t)= | z(t)u(t)+kδ(t) |
| y' (t)= | z' (t)u(t)+z0δ+kδ' |
| y" (t)= | z" (t)u(t)+z0' δ+z0δ' +kδ" |
| y(3)= | z(3)•u(t)+z0" δ+z0' δ' +z0δ" +kδ(3) |
 | |
| y(n)= | z(n)u(t)+z0(n−1)δ+  +z0δ(n−1)+kδ(n) +z0δ(n−1)+kδ(n) |
| [証明終] |
. .
微分方程式(3.32)の場合には、n の値は2であり、(3.36)に示した初期値は次のように得られる。
  | 1000 | 1001 | 1 |   |   | k |   | = |   | 1999 |   |
| 1001 | 1 | 0 | z0 | 1 | |||||||
| 1 | 0 | 0 | z0' | 0 | |||||||
| ∴ | k=0, | z0=1, | z0' =998 | ||||||||
| Y(s)= | Ts Ts+1 | •1 | y' + | 1 T | y=δ' (t) | (3.39) |
  |
1 T | . .1 |   |
  | k |   | = |   | 0 |   |
∴ | k=1, | z0= | −1 T | ∴ | y= | −1 T | e | −t T | u(t)+δ(t) | (3.40) |
| 1 | . .0 | z0 | 1 |
| y' + | 1 T | y=δ' (t)+ | 1 T | 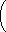 | 1−e | −t T | 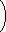 | δ(t) | (3.41) |
. . ラプラス変換では、分子を分母で割ることができ、伝達関数は
  | a0 | a1 | a2 |  | an−1 | 1 |   |   | 0 |   | = |   | b0 |   |
−k |   | a0 |   |
(3.42) |
| a1 | a2 |  | an−1 | 1 | 0 | z0 | b1 | a1 | |||||||||||
| a2 |  | an−1 | 1 | 0 | 0 | z0' | b2 | a2 | |||||||||||
 |  |  |  |  | |||||||||||||||
| an−1 | 1 | 0 |  | 0 | z0(n−2) | bn−1 | an−1 | ||||||||||||
| 1 | 0 |  | 0 | z0(n−1) | bn | 1 |
3.7 インパルス応答の数値シミュレータ
. .
任意の伝達関数のインパルス応答は定理 3.4 により同次微分方程式とその初期値に変換できるから、微分方程式の数値解法によりそれを求めることが出来る。従って、微分方程式の数値解法は任意のインパルス応答のシミュレータである。これはラプラス変換 Y(s)のポールを使用しないから非常に簡単で容易である。
. .
逆ラプラス変換はポールを求める数値解法、
. .
Y(s)が(3.43)で表されるとき、これを単精度で数値化した式は(3.44)で表される。判別式 D2は二つの定数の2進法における最小有効ビットの丸め誤差のために負の値となる。示された値は下に与えられた BASIC のプログラムによる結果である。従って、数値的なポールは二重ポールではなく、一対の複素数ポールとなり、大きさの略等しい複素数の差が桁落ちを起こさずに正しくもとまるなら、この逆ラプラス変換は(3.45)になる。これは(3.46)に示す解析的結果とは著しく異なる。
| Y(s)= | 1 s2+(44/7)s+(484/49) | (3.43) | Y(s)= | 1 s2+6.285714s+9.877551 | (3.44) |
| D2=6.2857142−4×9.877551=−3.814697×10−6 | jω=D/2=9.765625×10−4j |
| B=44/7:C=484/49:D2=B*B−4*C:D=SQR(−D2) | |
| y= | 1 ω | e−3.142857tsinωt | (3.45) | yt=te | −22t 7 | (3.46) |
. . Y(s)が(3.47)で表されるとき、これを単精度で数値化した式は(3.48)で表される。判別式 D2は下に与えられた BASIC のプログラムにより正の値になる。従って、数値的なポールは二重ポールではなく二つの殆ど等しいポールになり、逆ラプラス変換は(3.49)になる。これは(3.50)に示す解析的に求めた結果とは著しく異なる。
| Y(s)= | 1 s2+(72/13)s+(1296/169) | (3.47) | Y(s)= | 1 s2+5.538462s+7.668639 | (3.48) |
| D2=5.5384622−4×7.668639=1.907349×10−6 | D=1.381068×10−3 |
| B=72/13:C=1296/169:D2=B*B−4*C:D=SQR(D2) | |
| y= | 1 D | 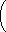 e−2.768540t−e−2.769921t e−2.768540t−e−2.769921t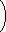 | (3.49) | yt=te | −36t 13 | (3.50) |
. . Table 3.1 及び 3.2 は上記の結果と数値シミュレータの結果、即ち、可変刻み3分点法による微分方程式の数値解を示す。微分方程式の数値解法を用いる方法はポールを使用しないからこれらの問題を生じない。高次の伝達関数の場合には、この方法は更に簡単にして容易である。
. . Program 2.2 の副プログラムは次に示されている。56 行の BB 及び CC の値は 58 行で与えられねばならない。これを 56 行に十進少数で記述すると解に大きな誤差を生ずることとなる。
| Subroutines for Eq.(3.43) |
|---|
| 56 F=−BB*Y(2)−CC*Y(1):RETURN 58 XB=0:XE=30:N=300:ND=2:Y(2)=1:Y(1)=0:BB=44/7:CC=484/49:B2#=22#/7#:RETURN 60 Y#=X#*EXP(−B2#*X#):RETURN |
| Subroutine for Eq.(3.47) |
| 58 XB=0:XE=30:N=300:ND=2:Y(2)=1:Y(1)=0:BB=72/13:CC=1296/169:B2#=36#/13#:RETURN |
| Table 3.2 The case D2>0 by rounded error. | ||||||
|---|---|---|---|---|---|---|
| IB | EE | t | Laplace | Simulator | Accurate | exp |
| 1 2 3 4 5 6 7 8 9 10 15 20 25 30 35 40 45 50 60 70 80 90 100 150 200 250 260 270 280 290 300 |
4 8 8 16 8 8 8 4 4 4 4 2 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 6.0 7.0 8.0 9.0 10.0 15.0 20.0 25.0 26.0 27.0 28.0 29.0 30.0 |
7.5829260 1.1493075 1.3070513 1.3215093 1.2518086 1.1388416 1.0074244 8.7298602 7.4442796 6.2703721 2.3553682 7.8642648 2.4618818 7.3976151 2.1610798 6.1853134 1.7424429 4.8490278 3.6486452 2.6692597 1.9131514 1.3496389 9.4054035 1.3681575 1.7693020 2.1450040 1.3987099 9.1085960 5.9234641 3.8477601 2.4961132 |
7.5811274 1.1494700 1.3071419 1.3212813 1.2521005 1.1390801 1.0074764 8.7289229 7.4446961 6.2710218 2.3555843 7.8651421 2.4619882 7.3983805 2.1614885 6.1860657 1.7427557 4.8491265 3.6490809 2.6697400 1.9133717 1.3498644 9.4055813 1.3682550 1.7692994 2.1449140 1.3988892 9.1099043 5.9244493 3.8479376 2.4962690 |
7.58112819 1.14947008 1.30714199 1.32128144 1.25210048 1.13908007 1.00747644 8.72892306 7.44469664 6.27102248 2.35558508 7.86514460 2.46198784 7.39837479 2.16148535 6.18604995 1.74275013 4.84910729 3.64906330 2.66972510 1.91336070 1.34985690 9.40553661 1.36825368 1.76928238 2.14486002 1.39884840 9.10960246 5.92423189 3.84778125 2.49615753 |
-02 -01 -01 -01 -01 -01 -01 -02 -02 -02 -02 -03 -03 -04 -04 -05 -05 -06 -07 -08 -09 -10 -12 -17 -23 -29 -30 -32 -33 -34 -35 |
| Table 3.1 The case D2<0 by rounded error. | ||||||
|---|---|---|---|---|---|---|
| IB | EE | t | Laplace | Simulator | Accurate | exp |
| 1 2 3 4 5 6 7 8 9 10 15 20 25 30 35 40 45 50 60 70 80 90 100 150 200 250 260 270 272 |
8 8 8 8 8 8 8 4 4 4 4 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 6.0 7.0 8.0 9.0 10.0 15.0 20.0 25.0 26.0 27.0 27.2 |
7.3031031 1.0667063 1.1685400 1.1378624 1.0387408 9.1032371 7.7562213 6.4736538 5.3187482 4.3159299 1.3449397 3.7254493 9.6744415 2.4118152 5.8455844 1.3878954 3.2437426 7.4875703 3.8778914 1.9526134 9.6312208 4.6763544 2.2425307 5.0372520 1.0057567 1.8826088 8.4501330 3.7872693 0.0000000 |
7.3031038 1.0667065 1.1685402 1.1378627 1.0387410 9.1032393 7.7562220 6.4736553 5.3187493 4.3159310 1.3449405 3.7254544 9.6744596 2.4118229 5.8456051 1.3879015 3.2437570 7.4876061 3.8779149 1.9526267 9.6313131 4.6764090 2.2425613 5.0374123 1.0058035 1.8827438 8.4508017 3.7875821 2.0350776 |
7.30310346 1.06670639 1.16854005 1.13786250 1.03874094 9.10323861 7.75622124 6.47365522 5.31874923 4.31593093 1.34494024 3.72545195 9.67444862 2.41181899 5.84559528 1.38789922 3.24375241 7.48759648 3.87791391 1.95262767 9.63132129 4.67641321 2.24256404 5.03742439 1.00581870 1.88279114 8.45103635 3.78769387 2.03513807 |
-02 -01 -01 -01 -01 -02 -02 -02 -02 -02 -02 -03 -04 -04 -05 -05 -06 -07 -08 -09 -11 -12 -13 -20 -26 -33 -35 -36 -36 |