3.8 注意すべき問題
. .
任意の同次微分方程式はその初期値と共に定理 3.4 により伝達関数に変換することが可能である。従って、微分方程式の数値解法において述べたように、この数値シミュレータは t=0 から遠くの点まで正確にインパルス応答を求めることが出来ない場合があるという問題があり得る。
. .
微分方程式が z" +3z' +2z=0 で初期値が z(0)=1 及び z' (0)=−2 のとき、y(t)=z(t)u(t)のラプラス変換は定理 3.4 及び k=0 により(3.51)で表される。この分子と分母にある s+1 を消去しない場合は、第1.7節の微分方程式の数値解の安定性で述べたように数値シミュレータは t の大きなところまで正確な解を得ることはできない。
  | 2 | 3 | 1 |   |   | 0 |   | = |   | 1 |   | ∴ | Y(s)= | s+1 s2+3s+2 | = | 1 s+2 | (3.51) |
| 3 | 1 | 0 | 1 | 1 | |||||||||||||
| 1 | 0 | 0 | −2 | 0 |
  | 2 | 20 | 1 |   |   | 0 |   | = |   | 20 |   | ∴ | Y(s)= | s+20 s2+20s+2 | (3.52) |
| 20 | 1 | 0 | 1 | 1 | |||||||||||
| 1 | 0 | 0 | 0 | 0 |
. . 数値計算は(π×10−9+π)−π のような場合には加法の結合則を満足しない。この場合単精度計算では結果は零であり、π×10−9ではない。二次方程式に起こる問題のように、これが数値計算結果の精度に大きな影響を与える場合が沢山ある。しかし、加法の結合則が満足されるためには π×10−9は零と考えるべきである。故に、微分方程式の数値解がその様な値にまで減衰したなら、それは零と考えるべきである。
. . それを有意な値であると考えるなら、それは、その値だけを 109倍に増幅したことになる。浮動小数点法はその増幅率を逆数で示している。自動制御システムは時間と共に変化する入出力データの大きさによって増幅率を変化させてはならない。
. . デイジタル方式はアナログ方式より精度がよいといわれる。それは、アナログ方式は殆どの場合有効桁3桁程度の精度であるのに対して、デイジタル方式は 7, 16, …… のように多くの有効桁を持つ精度が可能であるという意味であり、増幅率が可変であるということではない。
3.9 畳込み積分
. .
畳込み積分は(3.53)で表され、被積分関数と積分上限の2箇所に変数 t を持つ。従って、変数 t に関する微分は定理 3.5 に述べるように、どちらかの変数 t を定数と看做した二つの微分の和になる。故に、(3.54)で表される。
 | t | f(τ)g(t−τ)dτ = |  | t | f(t−τ)g(τ)dτ | (3.53) |
| 0 | 0 |
| d dt |  | t | f(τ)g(t−τ)dτ=f(t)g(0)+ |  | t | f(τ) | d dt | g(t−τ)dτ | (3.54) |
| 0 | 0 |
. . [定理 3.5]. . 被積分関数及び積分上限が変数 t を持つとき、
| d dt |  | t | g(t, τ)dτ=g(t, t)+ |  | t | d dt | g(t, τ)dτ | (3.55) |
| 0 | 0 |
| [証明終] |
. . 畳込み積分は t の全範囲において定義されているので、そのラプラス変換は厳密には定理 3.6 に示すように
. .
[定理 3.6]. .
f(t)及び g(t)が二つの同次微分方程式の解であるとき、これらのラプラス変換の積は、
| F(s)•G(s)= |  | ∞ | e | −st | u(t) |  | t | f(τ)g(t−τ)dτdt | (3.56) |
| 0 | 0 |
| [証明] | G(s)= |  | ∞ | g(t)u(t)e | −st |
dt = |  | ∞ | g(t−τ)u(t−τ)e | −s(t−τ) | dt |
| 0 | τ |
| F(s)•G(s)= |  | ∞ | f(τ)u(τ)e | −sτ |
dτG(s)= |  | ∞ | f(τ)u(τ)e | −sτ |  | ∞ | g(t)u(t)e | −st | dtdτ |
| 0 | 0 | 0 |
=  | ∞ |  | ∞ | f(τ)u(τ)g(t−τ)u(t−τ)e | −st | dtdτ | |
| 0 | τ |
| F(s)•G(s)= |  | ∞ |  | t | f(τ)u(τ)g(t−τ)u(t−τ)e | −st | dτdt= |  | ∞ | e | −st | u(t) |  | t | f(τ)g(t−τ)dτdt |
| 0 | 0 | 0 | 0 |
| [証明終]__________ |
. . h(t)が伝達関数G(s)のインパルス応答のとき、g(t)を定理 3.4 による初期値を持つ同次微分方程式の解とすると、h(t)=L−1{G(s)×1}=kδ(t)+g(t)u(t)であることは既に述べた。このインパルス応答は又 h(t)=L−1G(s)と表される。従って、δ(t)は h(t)との畳込み積分において何の影響も与えないことが成立しなければならない。
| . . [定理 3.7] |  | t | δ(τ)δ(t−τ)dτ=δ(t) | (3.57) |
| 0 |
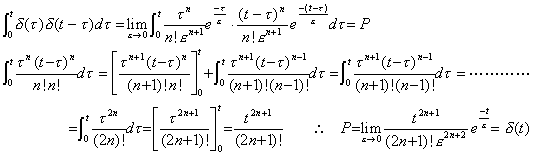 [証明終]
[証明終]| . . [定理 3.8] |  | t | h(τ)δ(t−τ)dτ=h(t), . .where. . h(t)=kδ(t)+g(t)u(t) | (3.58) |
| 0 |
 | t | {kδ(τ)+g(τ)u(τ)}δ(t−τ)dτ= kδ(t)+g(t)u(t) |  | t | δ(t−τ)dτ= kδ(t)+g(t)u(t) |
| 0 | 0 | [証明終] |
. . [定理 3.9]. .kfδ(t)+f(t)u(t) 及び h(t)=khδ(t)+g(t)u(t)のラプラス変換をそれそれ F(s) 及び G(s)で表すと、
 | ∞ | e | −st |  | t | h(τ){k | f | δ(t−τ)+f(t−τ)u(t−τ)}dτdt= G(s)•F(s) | (3.59) |
| 0 | 0 |
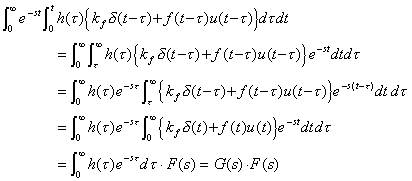 [証明終]
[証明終]. .
上の定理により、h(t)と δ(t)の畳込み積分が零なら、関数 h(t)は恒等的に零である。故に、ラプラス変換 H(s)×1 が零なら H(s)は零、即ち、関数 h(t)は恒等的に零である。この関係は任意の二つの関数の畳込み積分についても同様である。
. .
インパルス応答 h(t)は t≤0 では零であるから、ラプラス変換演算は h(t)の畳込み積分に u(t)を掛ける必要はない。kf=kh=0 の場合、定理 3.9 は定理 3.6 と等価であり、h(t)=g(t)u(t)であるからこの場合の畳込み積分に u(t)を掛ける必要はない。
. .
ラプラス変換可能な関数は、δ(t)及びその導関数以外は分母より次数の低い分子を持つラプラス変換となる。従って、そのような関数 F(s)によって伝達関数 G(s)が駆動された場合の応答が Y(s)なら、駆動関数は f(t)u(t)であり、応答 y(t)は h(t)と f(t)の畳込み積分で表される。故に、それは次に示すように y(t)=z(t)u(t)と表される。
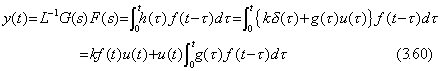
3.10 任意関数に駆動される微分方程式と伝達関数
. .
Y(s)が F(s)に駆動される伝達関数 G(s)の応答であるとき、(3.61)で表される。定理 3.3 の証明により f(t)u(t)及びその全ての導関数の t=0 における値は零である。y(t)及びその全ての導関数の t=0 における値も、(3.60)により
| Y(s)= G(s)F(s)= | bnsn+bn−1sn−1+bn−2sn−2+  +b0 +b0sn+an−1sn−1+an−2sn−2+  +a0 +a0 | F(s) | (3.61) |
y(n)+an−1y(n−1)+an−2y(n−2)+  +a0y= bn{f •u}(n)+bn−1{f•u}(n−1)+ +a0y= bn{f •u}(n)+bn−1{f•u}(n−1)+  +b0{f•u} +b0{f•u} | (3.62) |
| z(t)= kf(t)+ |  | t | g(τ)f(t−τ)dτ | (3.63) |
| 0 |
. . [定理 3.10]. .z(t)は次の微分方程式の解である。
z(n)+an−1z(n−1)+an−2z(n−2)+  +a0z= bnf(n)+bn−1f(n−1)+ +a0z= bnf(n)+bn−1f(n−1)+  +b0f +b0f | (3.64) | ||||||||||||||||||||||||||||||||||||||||||||||
| (3.65) |
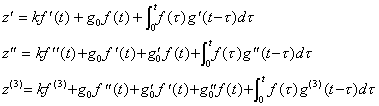 ___.  |
h(n)+an−1h(n−1)+  +a0h= bnδ(n)+bn−1δ(n−1)+ +a0h= bnδ(n)+bn−1δ(n−1)+  +b0δ +b0δ |
g(n)+an−1g(n−1)+  +a0g=0 +a0g=0 |
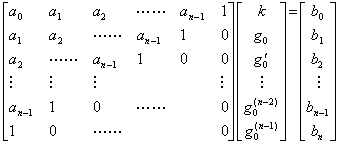
. . 初期値(3.65)は z(t)及び上記の導関数に t=0 を代入すれば得られる。
| [証明終] |
| . . [定理 3.11]. . (3.65)は次式に等しい。 | AZ=FTB | (3.66) |
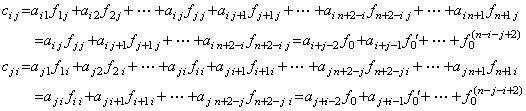
| AZ=AFG=AFA−1B=FTATA−1B=FTB | [Q.E.D.] |
. . y(t)=z(t)u(t)が微分方程式(3.62)を満たすことは容易に示される。y(t)及び
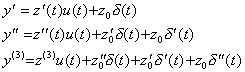 | ||
 | (3.67) | |
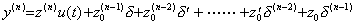 | ||
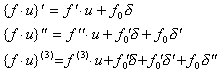 | ||
 | ||
| . .例題 1.. .Y(s)= | s−a s+a | • | 1 s2 | . .は微分方程式 y' +ay={tu(t)}' −atu(t) | ,. .y(0)=0 | (3.68) |
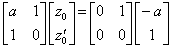 . .即ち、 z0=0.
. .即ち、 z0=0.
| 一般解は . .z= | 2 a | −t+C | e | −at | . .であり、積分定数は z(0)=0 により | . .C= | −2 a |
. .
例題 2.. .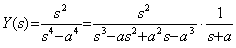
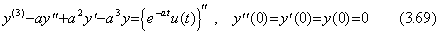
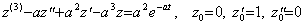 である。何故ならば、
である。何故ならば、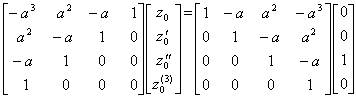 .
.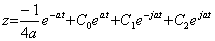 であり、
であり、積分定数は、
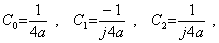 . .故に、
. .故に、 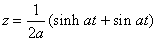
. . 数値解は、微分方程式の数値解法を用いて微分方程式(3.64)を(3.66)の初期値の基で解けば簡単に得られる。この方法はポールを使用しないから複素数の計算を必要としない。
3.11 簡単な解法
. .
関数 f(t) の微分が困難な場合には、微分方程式(3.64)の右辺は数値微分法によって得ることが出来る。しかし、精度に関して多少問題があるかもしれない。この問題は次の定理により回避することが出来る。
. .
[定理 3.12]. .
微分方程式(3.62)は次の微分方程式に等しい。
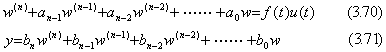
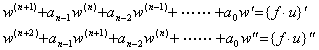 |
 |
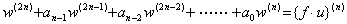 |
| [証明終] |
. . 微分方程式(3.70)の解は w=z(t)u(t)であり、z(t)は定理 3.10 及び 3.11 により、微分方程式(3.72)の全初期値が零に対する解である。(3.71)に示した解 y(t)は(3.73)により得られる。何故なら、(3.67)の全ての初期値が零の場合により示されるように、全ての導関数は w(k)=z(k)(t)u(t)であるから。
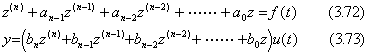
. . 前記の例題 1 の場合、微分方程式(3.72)は z' +az=t, z(0)=0 となり、その解は
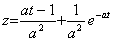 . .故に、
. .故に、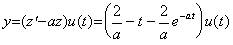
. . 前記の例題 2 の場合、微分方程式(3.72)は次のようになる。
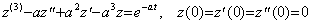
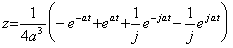
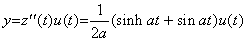
. . 数値解法の場合、z(n−1) から z' 迄の全ての微係数は微分方程式を解く過程で z(n)を逐次に積分することにより得られる。従って、この数値解法は f(t)の初期値及び導関数を計算する必要がないので非常に簡単かつ容易である。
. . (3.61)の伝達関数 G(s)は次に示す二つの伝達関数 G1(s), G2(s)の積で表すことができる。
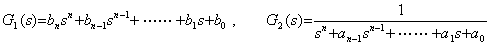
. . 微分方程式(3.62)を解く方法は G1(s)F(s)により駆動される伝達関数 G2(s)の応答を求めることと同じであり、定理 3.12 により解く方法は G2(s)F(s)により駆動される伝達関数 G1(s)の応答を求めることに同じである。従って、両者は同じことである。しかし、数値解法の場合には後者の方が優れている。
. . 伝達関数のインパルス応答は(3.62)の f(t)u(t)を δ(t)に置き換えた微分方程式の解である。従って、微分方程式は次のように変換される。
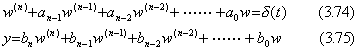
. . 微分方程式(3.74)は定理 3.4 により微分方程式(3.76)に同じであり、(3.67)及び、z0(n−1)=1 以外の全初期値が零であることにより、
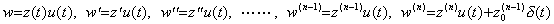
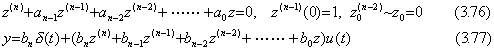
. .
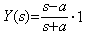 の場合は、微分方程式 z' +az=0, z(0)=1 の解は z=e−at である。故に、
の場合は、微分方程式 z' +az=0, z(0)=1 の解は z=e−at である。故に、
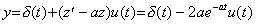
. . 硬い微分方程式といわれる連立微分方程式(3.78)の場合、(3.79)に示すようにラプラス変換することにより解くことが出来る。z(t)は微分方程式(3.80)の解であり、(3.81)となるから、解 y1 及び y2は(3.82)で表される。
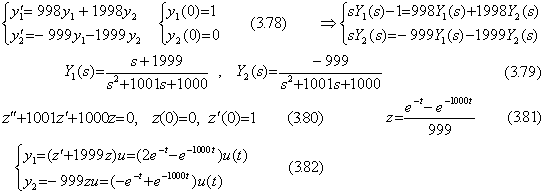
. .
数値解法の場合には、第 1.5 節で述べたように、微分方程式(3.80)は(3.83)に示す解の存在条件を必要とする。その条件は h<0.000998 となる。但し、h は著者の3分点法及び Runge-Kutta法の場合にはステップ幅の半分である。 t=0 の近傍で正確な解を得るためには h の値はもっと厳しい条件を満たさねばならない。しかし、その条件は解が分からなければ得られない。この問題は、第 2.3 節で述べた著者の可変刻み幅3分点法により解決できる。
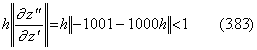
3.12 数値シミュレータのプログラム
. .
数値シミュレータのプログラムは印刷手続き以外は n 階の微分方程式の解法である Program 2.2 と同じものである。印刷手続きは、次に示すように伝達関数の分子を計算する副プログラムが必要である。
|
54 IF EB<EE THEN RETURN ELSE GOSUB 55:YY#=G:X#=X2:GOSUB 60:LOCATE 40,CSRLIN . . :PRINT USING"Y=##.#######^^^^ True=##.########^^^^";YY#;Y#:RETURN 55 G=Y(2)+1999*Y(1):RETURN 56 F=-1001*Y(2)-1000*Y(1):RETURN 58 XB=0:XE=50:N=500:ND=2:Y(1)=0:Y(2)=1:RETURN 60 Y#=2*EXP(-X#)-EXP(-1000*X#):RETURN [Note] Y(k+1)=z(k), ND=n-th order, N=the number of equidistances between XB to XE. |
. .
58 行で与えられた等間隔点における結果のみを印刷するために、結果を印刷する副プログラムである 54 行の先頭に"IF EB<EE THEN RETURN ELSE"が付加されている。54 行の"YY#=Y(1)"も"GOSUB 55:YY#=G"で置き換えられている。 55 行は(3.73)及び(3.77)の多項式の値を与える。但し、 Y(k+1)は z(k)の値を持つ。56 行は次のように微分方程式(3.72)の z(n)の値を与える。
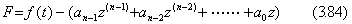
. . 上記の副プログラムは(3.79)の伝達関数 Y1(s)のインパルス応答をシミュレートしている。次の表はその結果を示す。EE の値は各ステップ毎の最後の積分間隔が 0.1÷EE であることを示す。最初のステップ区間[0, 0.1]において t=0 の近傍では EE の値は約 4000 にもなる。
| Table 3.3 Impulsive response of Y1(s). | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IB | EE | t | y1 | Accurate | exp | IB | EE | t | y1 | Accurate | exp | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
64 64 64 64 64 64 128 64 64 64 64 64 32 64 64 32 64 32 32 32 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
1.8096750 1.6374615 1.4816363 1.3406391 1.2130605 1.0976226 9.9317008 8.9865738 8.1313872 7.3575842 6.6574168 6.0238808 5.4506326 4.9319360 4.4625986 4.0379262 3.6536667 3.3059734 2.9913682 2.7067021 |
1.80967483 1.63746150 1.48163642 1.34064008 1.21306132 1.09762325 9.93170619 8.98657918 8.13139290 7.35758882 6.65742152 6.02388395 5.45063547 4.93193940 4.46260320 4.03793026 3.65367031 3.30597753 2.99137246 2.70670566 |
00 00 00 00 00 00 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 |
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
32 64 64 64 128 64 64 32 32 32 32 32 128 128 64 64 128 32 64 64 |
2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4.0 |
2.4491251 2.2160603 2.0051749 1.8143575 1.6416985 1.4854699 1.3441086 1.2162002 1.1004636 9.9574067 9.0098321 8.1524305 7.3766239 6.6746421 6.0394671 5.4647338 4.9446959 4.4741459 4.0483732 3.6631193 |
2.44912821 2.21606306 2.00517697 1.81435889 1.64169997 1.48547135 1.34411019 1.21620131 1.10046430 9.95741367 9.00983919 8.15244041 7.37663383 6.67465336 6.03947668 5.46474371 4.94470506 4.47415458 4.04838190 3.66312778 |
-01 -01 -01 -01 -01 -01 -01 -01 -01 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 | |
3.13 最も重要なアイディア
. .
上記に述べた方法は、ある問題を解く方法は一つだけではないことを示す。もし、関数表現された応答を得たいなら逆ラプラス変換が簡単であり優れている。しかし、数値データで表された応答を得たいなら n 階の微分方程式の数値解法が、ポールの計算も複素数の使用も必要ないので、簡単であり優れている。
. .
アナログコンピュータは高次の伝達関数を一次および二次の伝達関数の組み合わせでシミュレートする。これは逆ラプラス変換のシミュレーション、即ち、積分機構のシミュレーションに等価である。ディジタルコンピュータも同様の方法でシミュレートすることもできる。しかし、著者の n 階の微分方程式の数値解法でシミュレートするほうがシミュレーション言語の必要もなく、簡単で優れている。これは微分方程式のシミュレーションであり、微分方程式がラプラス変換で表せないようなシステムもシミュレートできる。
. .
これらは、アナログシステムでは簡単ではなくても、ディジタルシステムではその問題を解く簡単にして優れた方法があり得ることを示す。著者は、脳は自動制御機構であると考えているが、そのシミュレーションについても同様のことが言える。この考えが音声の合成と認識及び超並列処理に関する新しい、簡単な方法を開発することとなる。