Definite Integral (c) 1998 Akio Wakabayashi

2.7　微分方程式の数値解法による定積分
. . 関数 f(t) のａからｂ迄の定積分は(2.5)に示された微分方程式の t=b における数値解に等しい。著者の可変刻み３分点法は前もって与えられたステップ幅2hを変化させることなく解を得る。そして、その解は常に正しいとは限らない。その理由は、この微分方程式は解 y を右辺に持たないから、ステップ幅が幾らでも３回の反復における最後の修正値は常に１回目及び２回目の修正値と等しいことにある。

. . しかしながら、解 y と関数 f(t)は互いに独立ではないので、区分幅ｈ、即ち、ステップ幅の２分の１は第1.5節の定理1.4より(2.6)で表される解の存在条件を十分に満足しなければならない。
Eq2_6

. . もっと正確な解を得るためには、微分方程式はその右辺にｙ又はその微係数を持つ高階の微分方程式に変換されなければならない。この方法は下記の悪条件を持つ定積分を安定に計算できる。これらの例題は情報処理学会誌(2/'98)に掲載されている。
Eq2_7

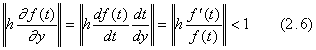
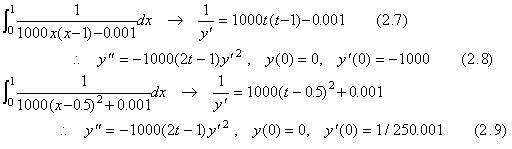
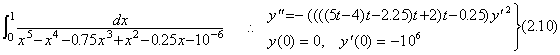
. . 微分方程式(2.8)は関数 1000(2t−1)が y' に関して一定であると仮定できる狭い範囲に対しては解の存在条件(2.11)を持つ。これは、ｈの値は t=0 及び t=1 の近傍では非常に小さくなければならないが、0.1<t<0.9 の範囲では非常に大きくてもよいことを示す。従って、第2.3節の Program 2.2 は 2h=0.02 の基本ステップ幅のような非常に大きな区間幅でこれを解くことができる。しかし、そのｈの値は t=0 の近傍では微係数の値が非常に大きいために計算でオーバーフローを起こす。
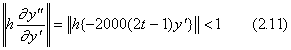
Eq2_11

. . オーバーフローを避けるためには、2ⁿ で且つ 8388609 より小さくなければならないが、適当な値を変数EEに予め代入しなければならない。この値は区分幅 2h の可変細分割数を示す。この代入文は Program 2.2 の58行に与えられ、その効果を得るために18行の先頭にある代入文"EE=1"は16行の先頭に移さねばならない。58行に代入文"EE=2ⁿ"が与えられていなければ16行の代入文"EE=1"が有効となる。更に、先頭に文字 E の付く変数の整数宣言を取り除き、変数 EB が偶数であることを検出する手順を与える必要がある。
. . これらの書き換え部分は Program 2.4 に太字を用いて示してある。Program 2.4 は又、数値解と比較するための真の解をプリントする文を持たず、60行は単に改行文だけを持つ。真の解が必要なら以下に示すように60行は X# を用いてそれを計算し、プリントする文を持たねばならない。但し、 X# は X2 の末尾に零を付加した値でなければならない。

60 Y#=f(X#):PRINT USING"True=##.########^^^^";Y#:RETURN

Program 2.4

10 DIM Y0(6),Y1(6),Y2(6),Y(6):DEFINT J
12 DEF FNY1=(5*Y0(J3+1)+8*Y1(J3+1)-Y2(J3+1))*H3+Y0(J3):DEF FNY2=(Y0(J3+1)+
. . 4*Y1(J3+1)+Y2(J3+1))*H4+Y0(J3):DEF FNM=INT(EB-INT(EB/16384!)*16384!)MOD 2
14 RP=16777216#:RM=2/RP
16 EE=1:GOSUB 58:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE;" N=";N;" H=";H0:N1=ND+1
18 XL=XB:X=XB:GOSUB 48:FOR IB=1 TO N:ES=1:XI=XL:XL=XB+H0*IB:X0=XI
20 WHILE 2:H1=H0/EE:EB=ES:JM=FNM:WHILE EB=<EE:X2=XI+H1*EB:IF EB=EE THEN X2=XL
22 LOCATE 0,CSRLIN:PRINT"IB=";IB;" EB=";EB;" EE=";EE;" X=";X2;:GOSUB 46
24 FOR J3=1 TO ND:Y1(J3)=Y0(J3+1)*H+Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 50
26 FOR J3=1 TO ND:Y1(J3)=(Y0(J3+1)+Y1(J3+1))*H*.5+Y0(J3):Y2(J3)=Y1(J3+1)*H2+
. . Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52
28 IF ABS(Y2(ND))<1 THEN RA=RP ELSE RA=1
30 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52
32 R1=Y(ND)*RA
34 FOR J3=ND TO 1 STEP-1:Y1(J3)=FNY1:Y2(J3)=FNY2:Y(J3)=Y1(J3):NEXT:GOSUB 50:
. . GOSUB 52
36 R2=Y(ND)*RA:J3=ND:Y2(J3)=FNY2:Y(J3)=Y2(J3):R3=Y(ND)*RA:RA=RM*ABS(R3)
38 IF ABS(R2-R3)<RA THEN GOSUB 54:X=X2:GOSUB 48:X0=X2:GOSUB 42 ELSE IF EE
. . <8388608! THEN EE=EE*2:ES=EB*2-1:EB=EE+1 ELSE PRINT"EE>8388608!":END
40 EB=EB+1:JM=JM XOR 1:WEND:IF EB>EE+1 THEN WEND ELSE NEXT IB:END
42 IF ABS(R1-R3)<RA THEN IF EE>1 AND JM=0 THEN EE=EE/2:ES=EB/2+1:IF ES=<EE
. . THEN EB=EE+1 ELSE EB=EE
44 RETURN
46 H2=X2-X0:H=H1*.5:H3=H/12:H4=H2/6:X1=X0+H:RETURN
48 GOSUB 56:Y0(N1)=F:FOR J3=1 TO ND:Y0(J3)=Y(J3):NEXT:RETURN
50 X=X1:GOSUB 56:Y1(N1)=F:RETURN
52 X=X2:FOR J3=1 TO ND:Y(J3)=Y2(J3):NEXT:GOSUB 56:Y2(N1)=F:RETURN
54 YY#=Y(1):LOCATE 40,CSRLIN:PRINT USING" Y=##.#######^^^^ ";YY#;:X#=X2:
. . GOSUB 60:RETURN

56 F=-1000*(2*X-1)*Y(2)*Y(2):RETURN
58 XB=0:XE=1:N=50:ND=2:Y(1)=0:Y(2)=-1000:EE=65536!:RETURN
60 PRINT:RETURN
[Note] Y(k+1)=y^(k), ND=n-th order. N=the number of equidistances between XB to XE.

. . 上記プログラム及び(2.9)(2.10)の結果は Table 2.11, Table 2.12 及び Table 2.13 に示すように安定に得られる。しかし、t=1 におけるこれらの値は２乃至３桁の有効桁である。これらの解が大きな誤差を持つ原因は２つあり、それを取り除くのは容易に可能である。
. . Table 2.11 の t=0.5 における値は単精度で正しい。関数 y' (t)は直線 t=0.5 に対して対称であるから、t=1 における値はその２倍でなければならない。従って、誤差は 0.5 から 1 の範囲において生ずる。その原因の一つは Table 2.11 に示されるように h の値が１に対して無視できる値のために t の値が１の近辺では変化しないことにある。これは(h+t)−t の計算で結合則が成立しなくなり、(2.7)において等式(1−h){(1−h)−1}=h(h−1)が成立しない現象を惹き起こす。もう一つの原因は、微分方程式が解の存在条件の厳しくなる方向へ解かれるとき、数値解は少し精度が悪くなることである。

Table 2.12 The result of Eqs.(2.9)

58 XB=0:XE=1:N=50:ND=2:Y(1)=0:
. .Y(2)=1/250.001:RETURN

1
1
2
2
3
3
4
4
5
5
10
15
20
23
24
25
25
25
25
25
25
25
25
25
26
26
26
26
26
26
27
28
30
35
40
45
50

1
2
1
2
1
2
1
2
1
2
2
4
8
8
7
7
71
203
467
248
497
498
250
256
1
3
19
32
34
41
4
8
8
4
4
4
2

2
2
2
2
2
2
2
2
2
2
2
4
8
16
32
64
128
256
512
256
512
512
256
256
128
256
512
256
128
64
32
16
8
4
4
4
2

0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.2
0.3
0.4
0.45
0.464375
0.482187
0.491094
0.495859
0.498242
0.499375
0.499414
0.499453
0.499531
0.5
0.500156
0.500234
0.500742
0.5025
0.505313
0.512812
0.5225
0.55
0.6
0.7
0.8
0.9
1

4.0816158(-5)
8.3332983(-5)
1.2765902(-4)
1.7391227(-4)
2.2222122(-4)
2.7272600(-4)
3.2557984(-4)
3.8095051(-4)
4.3902217(-4)
4.9999746(-4)
1.3333234(-3)
2.9999593(-3)
7.9996558(-3)
1.7997207(-2)
2.6062449(-2)
5.4078560(-2)
1.0978933(-1)
2.3475608(-1)
5.1309919(-1)
9.9670964(-1)
1.0243102
1.0528332
1.1125995
1.5316864
1.6794735
1.7513239
2.1439555
2.6857326
2.8794148
2.9874856
3.0209548
3.0453715
3.0553691
3.0603690
3.0620351
3.0628688
3.0633688

Table 2.11 The result of Eqs.(2.8) by Program 2.4
IB	EB	EE	t	y
1 1 1 1 1 1 1 1 1 1 1 1 2 5 10 15 20 25 30 35 40 45 47 49 50 50 50 50 50 50 50 50 50 50 : :50	1 2 3 4 5 9 17 21 23 22 22 21 5 8 2 2 1 1 1 1 2 4 7 7 37 227 993 4067 16357 65507 262119 524267 524275 524276 : :524288	524288 524288 524288 524288 524288 262144 65536 16384 4096 1024 256 64 16 8 2 2 1 1 1 1 2 4 8 16 64 256 1024 4096 16384 65536 262144 524288 524288 524288 : :524288	3.8147(-8) 7.62939(-8) 1.14441(-7) 1.52588(-7) 1.90735(-7) 6.86645(-7) 5.18799(-6) 2.56348(-5) 1.12305(-4) 4.29687(-4) 1.71875(-3) 0.0065625 0.02625 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.9375 0.96875 0.991562 0.997734 0.999394 0.999858 0.999967 0.999991 0.999998 0.999999 0.999999 1 : : 1	-3.7437367(-5) -7.3523603(-5) -1.0835286(-4) -1.4200975(-4) -1.7457065(-4) -5.2274170(-4) -1.8226126(-3) -3.2822378(-3) -4.7301855(-3) -6.0658026(-3) -7.4516418(-3) -8.7958472(-3) -1.0202040(-2) -1.1618270(-2) -1.2429194(-2) -1.2968186(-2) -1.3410017(-2) -1.3815480(-2) -1.4220944(-2) -1.4662774(-2) -1.5201767(-2) -1.6012691(-2) -1.6523510(-2) -1.7249428(-2) -1.8581934(-2) -1.9902581(-2) -2.1222433(-2) -2.2669805(-2) -2.4100443(-2) -2.5328130(-2) -2.6502829(-2) -2.6958300(-2) -2.7122395(-2) -2.7158681(-2) : :-2.7508408(-2)

Table 2.13 The result of Eqs.(2.10)

56 F=-((((5*X-4)*X-2.25)*X+2)*X-.25)*Y(2)*Y(2):RETURN
58 XB=0:XE=1:N=50:ND=2:Y(1)=0:Y(2)=-1E+6:EE=4096:RETURN

1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
10
13
15
20
23
24
25
25
25

1
2
9
19
20
21
21
22
21
21
20
4
4
4
4
1
1
4
8
8
1
3
69
207

131072
131072
65536
16384
4096
1024
512
256
128
64
32
16
8
4
4
1
2
4
8
16
32
64
128
256

1.52588(-7)
3.05176(-7)
2.74658(-6)
2.31934(-5)
9.76562(-5)
4.10156(-4)
8.20312(-4)
1.71875(-3)
3.28125(-3)
0.0065625
0.0125
0.025
0.05
0.08
0.1
0.2
0.25
0.3
0.4
0.45
0.460625
0.480937
0.490781
0.496172

-1.4974946(-1)
-2.9409441(-1)
-2.0909696(+0)
-7.6668930(+0)
-1.2942420(+1)
-1.8565838(+1)
-2.1325554(+1)
-2.4288406(+1)
-2.6895609(+1)
-2.9719023(+1)
-3.2393227(+1)
-3.5377960(+1)
-3.8604725(+1)
-4.1088379(+1)
-4.2424946(+1)
-4.8147083(+1)
-5.1261372(+1)
-5.5182976(+1)
-7.1188240(+1)
-9.9705544(+1)
-1.1463088(+2)
-1.8801512(+2)
-3.3609390(+2)
-7.0923834(+2)

25
26
26
26
27
28
28
30
35
38
40
45
48
48
49
50
50
50
50
50
50
50
50
50

128
11
35
38
5
7
8
8
4
2
2
1
2
8
11
39
229
995
4067
16359
65515
262133
524283
524288

128
256
128
64
32
16
16
8
4
4
2
1
4
8
16
64
256
1024
4096
16384
65536
262144
524288
524288

0.5
0.500859
0.505469
0.511875
0.523125
0.54875
0.55
0.6
0.7
0.75
0.8
0.9
0.95
0.96
0.97375
0.992187
0.997891
0.999434
0.999858
0.999969
0.999994
0.999999
1
1

-2.6021067(+3)
-3.3845398(+3)
-4.6770024(+3)
-4.9263677(+3)
-5.0333604(+3)
-5.0927793(+3)
-5.0941147(+3)
-5.1201094(+3)
-5.1333867(+3)
-5.1362910(+3)
-5.1384429(+3)
-5.1419985(+3)
-5.1441265(+3)
-5.1447036(+3)
-5.1457168(+3)
-5.1483579(+3)
-5.1510396(+3)
-5.1536812(+3)
-5.1564380(+3)
-5.1594126(+3)
-5.1621450(+3)
-5.1643613(+3)
-5.1649092(+3)
-5.1651519(+3)

. . この誤差を避けるため、積分範囲を[0, 0.5] と [0.5, 1]の二つの積分に分けなければならない。そして２番目の積分範囲は左に１移動されなければならない、即ち、 y' (t)は u=t−1 を代入して変数 u の関数にしなければならない。更に、その積分範囲の積分は(2.12)に示すように 0 から −0.5 へと実行されねばならない。その積分値は下記の副プログラムを与えられた Program 2.4 により得られ、0 と 0.5 の間の積分値と符合が変わる以外同じになる。

=−1.3815480×10⁻²−1.3815480×10⁻²=−2.7630960×10⁻² 第２項の微分方程式は次のようになる。

56 F=-1000*(2*X+1)*Y(2)*Y(2):RETURN
58 XB=0:XE=-0.5:N=25:ND=2:Y(1)=0:Y(2)=-1000:EE=65536!:RETURN

. .
Table 2.12 は(2.9)の微分方程式は t=0.5 の極近傍で解の存在条件が一層厳しくなることを示す。従って、(2.9)の被積分関数は 0.5 左へシフトし以下のように積分しなければならない。

=1.5687959−(−1.5687959)=3.1375918 このとき微分方程式は次のようになる。

この場合、EE の値は基本分割数 N=25 に対して 256 を与えればよい。
. . Table 2.13 は(2.10)の微分方程式は t=0, t=0.5 及び t=1 の極近傍で解の存在条件が一層厳しくなることを示す。従って、積分範囲は[0, 0.25][0.25, 0.5][0.5, 0.75] 及び [0.75, 1]の四つに分けなければならない。第２及び第３範囲は 0.5 左へシフトしなければならず、第４範囲は１左へシフトしなければならない。これらの範囲の積分は以下のように行わねばならない。

=−51.261383−2565.9854+(−2549.3049)−28.693586=−5195.2452 ここで、0.25≤t≤1 の微分方程式は次のようになる。
Eq2_17

. . これら三つの例の定積分の結果は全て単精度で有効であり、クロック 10 MHz の 8086 CPU を用いたコンピュータで２乃至４分を要する。

目　次　へ