2. 演算子法から導かれるその他の数値解法
2.1 高次多項式を用いる解法
. .
著者の演算子法から高次多項式を用いる多くの解法を導くことができる。等間隔が4点ならy3の予測子が(1.2)の手順[3]に追加され、その繰返しは行われない。次に、(2.1)に示すように手順[4]でy1, y2及びy3を修正し、これをもう2回繰り返す。 y3の修正子はSimpsonの3/8則と呼ばれる。
. .
等間隔点が5点ならy4の予測子が手順[4]に追加され、その繰返しは行われない。次に、(2.1)に示すように手順[5]でy1, y2, y3及びy4を修正し、これをもう2回繰り返す。y4の予測子はMilneの予測子と呼ばれ、手順[5]の最後の修正子はNewton-Cotesの5点則と呼ばれる。
| ||||||||||||||||||||||||||||||||||||||||||||
. . Program 2.1 は(2.1)に示した5点を使用する解法であり、通常の場合は、3点を用いる解法より精度の良い解を与える。
| Program 2.1 |
|
10 DIM Y0(6),Y1(6),Y2(6),Y3(6),Y4(6),Y(6):DEFINT E,J 12 DEF FNY1=(5*Y0(J3+1)+8*Y1(J3+1)-Y2(J3+1))*H3+Y0(J3): . . DEF FNY2=(Y0(J3+1)+4*Y1(J3+1)+Y2(J3+1))*H4+Y0(J3): . . DEF FNY3=(Y0(J3+1)+3*Y2(J3+1))*H5+Y0(J3) 14 DEF FNY4=(9*Y0(J3+1)+19*Y1(J3+1)-5*Y2(J3+1)+Y3(J3+1))*H6+Y0(J3): . . DEF FNY6=(Y0(J3+1)+3*Y1(J3+1)+3*Y2(J3+1)+Y3(J3+1))*H8+Y0(J3): . . DEF FNY7=(2*Y1(J3+1)-Y2(J3+1)+2*Y3(J3+1))*H9+Y0(J3) 16 DEF FNY8=(251*Y0(J3+1)+646*Y1(J3+1)-264*Y2(J3+1)+106*Y3(J3+1)-19*Y4(J3+1))*H10+Y0(J3): . . DEF FNY9=(29*Y0(J3+1)+124*Y1(J3+1)+24*Y2(J3+1)+4*Y3(J3+1)-Y4(J3+1))*H11+Y0(J3): . . DEF FNY10=(9*Y0(J3+1)+34*Y1(J3+1)+24*Y2(J3+1)+14*Y3(J3+1)-Y4(J3+1))*H12+Y0(J3) 18 DEF FNY11=(7*Y0(J3+1)+32*Y1(J3+1)+12*Y2(J3+1)+32*Y3(J3+1)+7*Y4(J3+1))*H13+Y0(J3) 20 GOSUB 54:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE;" N=";N;" H=";H0:N1=ND+1 22 X4=XB:FOR IB=1 TO N:X0=X4:X4=XB+H0*IB:FOR J3=1 TO ND:Y0(J3)=Y(J3):NEXT 24 LOCATE 0,CSRLIN:PRINT"IB=";IB;" X=";X4;:GOSUB 40:X=X0:GOSUB 52:Y0(N1)=F 26 FOR J3=1 TO ND:Y1(J3)=Y0(J3+1)*H+Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 42 28 FOR J3=1 TO ND:Y1(J3)=(Y0(J3+1)+Y1(J3+1))*H*.5+Y0(J3): . . Y2(J3)=Y1(J3+1)*H2+Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 42:GOSUB 44 30 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:Y3(J3)=FNY3:Y(J3)=Y1(J3):NEXT: . . GOSUB 42:GOSUB 44:GOSUB 46 32 FOR J3=1 TO ND:Y1(J3)=FNY4:Y2(J3)=FNY2:Y3(J3)=FNY6:Y4(J3)=FNY7: . . Y(J3)=Y1(J3):NEXT:GOSUB 42:GOSUB 44:GOSUB 46:GOSUB 48 34 FOR J3=1 TO ND:Y1(J3)=FNY8:Y2(J3)=FNY9:Y3(J3)=FNY10:Y4(J3)=FNY11: . . Y(J3)=Y1(J3):NEXT:GOSUB 42:GOSUB 44:GOSUB 46:GOSUB 48 36 FOR J3=ND TO 1 STEP-1:Y1(J3)=FNY8:Y2(J3)=FNY9:Y3(J3)=FNY10: . . Y4(J3)=FNY11:Y(J3)=Y1(J3):NEXT:GOSUB 42:GOSUB 44:GOSUB 46: . . GOSUB 48:J3=ND:Y4(J3)=FNY11:Y(ND)=Y4(ND) 38 GOSUB 50:NEXT IB:END 40 HM=X4-X0:H=H0*.25:H2=H0*.5:H1=H0*.75:H3=H/12:H4=H2/6:H5=H1/4: . . H6=H/24:H8=H1/8:H9=HM/3:H10=H/720:H11=H/90:H12=H1/80:H13=HM/90: . . X1=X0+H:X2=X0+H2:X3=X0+H1:RETURN 42 X=X1:GOSUB 52:Y1(N1)=F:RETURN 44 X=X2:FOR J3=1 TO ND:Y(J3)=Y2(J3):NEXT:GOSUB 52:Y2(N1)=F:RETURN 46 X=X3:FOR J3=1 TO ND:Y(J3)=Y3(J3):NEXT:GOSUB 52:Y3(N1)=F:RETURN 48 X=X4:FOR J3=1 TO ND:Y(J3)=Y4(J3):NEXT:GOSUB 52:Y4(N1)=F:RETURN 50 X#=X4:GOSUB 56:YY#=Y(1):LOCATE 40,CSRLIN:PRINT USING . . "Y=##.#######^^^^ True=##.########^^^^";YY#;Y#:RETURN
52 F=100*(SIN(X)-Y(1)):RETURN |
2.2 プログラム2.1の結果の精度
| Table 2.1 Results of y' =100(sin t −y), y(0)=0 | |||||
|---|---|---|---|---|---|
| t | 5 points method | 3 points method | Accurate solution | 10n | |
| step=0.01 | step=0.02 | step=0.01 | |||
| 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20 |
3.6785675 1.1352742 2.0495741 3.0177429 4.0055022 5.0001778 5.9970450 6.9943026 7.9912253 8.9874841 9.9828921 1.0977320 1.1970656 1.2962799 1.3953644 1.4943098 1.5931056 1.6917419 1.7902094 1.8884978 |
: 1.1305087 : 3.0164769 : 4.9999267 : 6.9942616 : 8.9874819 : 1.0977326 : 1.2962806 : 1.4943106 : 1.6917431 : 1.8884990 |
3.6805207 1.1354182 2.0496540 3.0177828 4.0055208 5.0001867 5.9970498 6.9943063 7.9912283 8.9874871 9.9828951 1.0977323 1.1970660 1.2962803 1.3953649 1.4943101 1.5931059 1.6917424 1.7902099 1.8884982 |
3.67875972 1.13528838 2.04958203 3.01774709 4.00550414 5.00017871 5.99704594 6.99430354 7.99122609 8.98748430 9.98289234 1.09773202 1.19706571 1.29628001 1.39536462 1.49430988 1.59310573 1.69174212 1.79020948 1.88849783 |
-03 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -01 -01 -01 -01 -01 -01 -01 -01 -01 |
. . 両解法の1ステップの解の差分が同じなら5点法が3点法より約2桁精度の良い解を得る。しかし、5点法の区分幅hは3点法の半分であり、この比較は公正でない。その理由は、解法が同じでも区分幅が小さいほど解の精度は良いからである。故に、区分点数の異なった解法をすべて同じ条件で比較することはできない。しかし、Table 2.1から5点法が3点法より精度が良いといってよい。
. . Table 2.2において、ステップ幅0.2の5点法及びステップ幅0.1の3点法のt<5の範囲にわたって見られるように、1ステップの解の差分が小さければ5点法の方が3点法よりも精度が良い。しかし、t=10の近辺では前者は後者よりやや精度が悪い。h=0.1の場合は、解の存在条件はt>6.2の範囲にわたって満たされているが、ステップ幅0.4の5点法はあたかもMilne法の解であるかのごとく、精度の悪い解を示す。一方、ステップ幅0.2の3点法は未だそのような現象を示さない。
| Table 2.2 Comparison of results for y' =−ty, y(0)=10 | ||||||
|---|---|---|---|---|---|---|
| t | 5 points method | 3 points method | Accurate solution | 10n | ||
| step=0.2 | step=0.4 | step=0.1 | step=0.2 | |||
| 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0 6.2 6.4 6.6 6.8 7.0 7.2 7.4 7.6 7.8 8.0 8.2 8.4 8.6 8.8 9.0 9.2 9.4 9.6 9.8 10.0 |
9.8019867 9.2311630 8.3527012 7.2614899 6.0653062 4.8675218 3.7531109 2.7803729 1.9789866 1.3533529 8.8921607 5.6134742 3.4047434 1.9841090 1.1108987 5.9760120 3.0887051 1.5338017 7.3179612 3.3545773 1.4774466 6.2519166 2.5417918 9.9286321 3.7261707 1.3435525 4.6544174 1.5491348 4.9535777 1.5217796 4.4913250 1.2734457 3.4685890 9.0755092 2.2809560 5.5062621 1.2766163 2.8423704 6.0765867 1.2472022 2.4571213 4.6453811 8.4258602 1.4657175 2.4442777 3.9057119 5.9762683 8.7508212 1.2251042 1.6381593 |
: 9.2311630 : 7.2614903 : 4.8675227 : 2.7803733 : 1.3533508 : 5.6133890 : 1.9839504 : 5.9740677 : 1.5320852 : 3.3431742 : 6.1933859 : 9.6927281 : 1.2681434 : 1.3573090 : 1.1355667 (exp) 6.69(-09) : 2.06(-10) : -7.28(-13) : 3.47(-14) : -3.68(-15) : 6.79(-16) : -1.96(-16) : 8.48(-17) : -5.25(-17) : 4.56(-17) |
9.8019867 9.2311630 8.3527012 7.2614894 6.0653052 4.8675203 3.7531087 2.7803702 1.9789841 1.3533506 8.8921440 5.6134635 3.4047377 1.9841076 1.1109003 5.9760425 3.0887391 1.5338328 7.3182075 3.3547555 1.4775656 6.2526530 2.5422205 9.9309967 3.7274011 1.3441613 4.6572768 1.5504139 4.9590409 1.5240036 4.4999805 1.2766615 3.4800143 9.1143482 2.2935817 5.5455442 1.2883097 2.8756873 6.1674662 1.2709271 2.5164109 4.7872358 8.7506370 1.5368828 2.5935047 4.2051071 6.5509282 9.8055567 1.4101849 1.9485392 |
9.8019867 9.2311630 8.3526993 7.2614827 6.0652909 4.8674970 3.7530768 2.7803323 1.9789442 1.3533131 8.8918263 5.6132221 3.4045735 1.9840091 1.1108503 5.9758529 3.0887170 1.5338806 7.3188320 3.3552786 1.4779235 6.2547845 2.5433497 9.9363431 3.7296551 1.3449844 4.6597006 1.5508344 4.9579864 1.5224336 4.4895756 1.2712722 3.4557770 9.0159480 2.2568303 5.4178759 1.2467912 2.7487145 5.8011950 1.1710647 2.2586831 4.1569938 7.2895571 1.2156665 1.9237984 2.8812736 4.0709053 5.4053022 6.71(-21) 7.75(-22) |
9.80198673 9.23116344 8.35270199 7.26149030 6.06530660 4.86752228 3.75311111 2.78037290 1.97898674 1.35335283 8.89216081 5.61347500 3.40474421 1.98410974 1.11089965 5.97602198 3.08871441 1.53380989 7.31802551 3.35462628 1.47748183 6.25214775 2.54193577 9.92949522 3.72665317 1.34381028 4.65571332 1.54975396 4.95639984 1.52299797 4.49634149 1.27540685 3.47589347 9.10145896 2.28973485 5.53459867 1.28533632 2.86797709 6.14838727 1.26641655 2.50622581 4.76528183 8.70539806 1.52797740 2.57675711 4.17501738 6.49931301 9.72094942 1.39694133 1.92874985 |
00 00 00 00 00 00 00 00 00 00 -01 -01 -01 -01 -01 -02 -02 -02 -03 -03 -03 -04 -04 -05 -05 -05 -06 -06 -07 -07 -08 -08 -09 -10 -10 -11 -11 -12 -13 -13 -14 -15 -16 -16 -17 -18 -19 -20 -20 -21 |
. . Table 2.3はh=0.1 間隔の真の解と、t0が6.9より大きいところでは上記の条件が満たされないことを示す。定理2.1は区分幅hで満たされれば十分であることを示すものではなく、理想的には1ステップ区間で満たされることが望ましい。区分幅h=0.1のとき、5点法の1ステップ区間は4h=0.4であり、その間の解はt=6.0の近傍では出発値の1/10以下になるため解の精度は有効桁1桁程度であり不安定現象といわれる状態になっていく。3点法の1ステップ区間は2h=0.2であるから、その間の解は出発値の1/4以上あるため解の精度は有効桁3桁程ある。5点法で1ステップの解が出発値の1/4程度なのはt=3.2の近傍であり、解の精度は有効桁4桁である。いわゆる高次解法の不安定現象は著者の解法では単なる区分幅選定の不適当によるものであり、高次解法が不安定なのではない。3点法でも1ステップ区間が0.3、即ち、h=0.15であるとt=8の近傍で不安定現象といわれる状態が見られる。Runge-K法でも同様であり、微分方程式の解によるが固定区分幅解法である限りこの現象は生ずる。
| Table 2.3 | ||
|---|---|---|
| t | accurate y | exp |
| 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 6.8 6.9 7.0 7.1 7.2 |
1.52299797 8.31670729 4.49634149 2.40671954 1.27540685 6.69158609 3.47589347 1.78755544 9.10145896 4.58795947 2.28973485 1.13137839 5.53459867 |
-07 -08 -08 -08 -08 -09 -09 -09 -10 -10 -10 -10 -11 |
. .
[定理 2.1]. .
微分方程式y' =f(y,t)の数式解が分かっているなら数値解の存在条件は次のようになる。
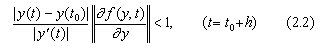
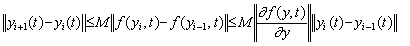
| |f(y(a),a)(t−t0)|≤M|f(y,t)| | (t0<a<t) | (2.3) |
| 故に、Mは |y(t)−y(t0)|=M|y' (t)| を満たさねばならない。 | [証明終] |
. .
微分方程式及び数値解法の次数により、区分幅がこの条件を満たすだけでは十分でない場合もある。十分な精度を得るためには理想的には1ステップ幅がこの条件を満たすことが望ましい。
. .
微分方程式 y' =−ty 及び t>t0の場合、y(t)<y(t0)であるから(2.2)は次のようになる。
| −y(t)+y(t0)<y(t) | ∴. .y(t)>y(t0)/2 |
. . 微分方程式 y' =100(sin t −y) 及び t>t0≈0の場合には、y(t0)<y(t)<sin tであるから(2.2)は次のようになる。
| y(t)−y(t0)<sin t −y(t) | ∴. .y(t)<{y(t0)+sin t}/2 |
. . 定理 1.4 はf(y(a),a)がf(y,t0+h)に殆ど等しいことが必要である。一方、定理 2.1 はその条件を必要としない。それ故、より正確な解の存在条件を与える。しかし、解が既知であることを必要とする。従って、解の存在条件を見積もるためには使えないが、異常解の原因の調査、即ち、区分幅やステップ幅の適否を得られた数値解を使用して検討するために役に立つ。
2.3 可変刻み3分点法
. .
硬い微分方程式(1.16)は全範囲にわたって100h<1なる条件を必要とする。しかし、微分係数dt/dyが無視し得ない範囲にまで正確な解を得るためにはその条件は十分ではない。t=0の近傍ではその条件は(1.17)で表されるべきであり、正確な解を得ることは非常に厳しい。硬い微分方程式(1.18)もまた厳しい条件h<0.000998を必要とし、t=0 の近傍では、他の範囲における解と同じ程度の精度の解が要求されるとき更に厳しいものとなる。しかし、その条件は t と y' の関係が明示されていないので得られない。
. .
著者の解法は区分幅の条件を計算することなく可変ピッチ法を用いて正確な解を得ることが出来る。その解法は極めて簡単である。何故なら、(1.2)の3回繰り返される手順[3]は適当な条件を検出することの出来るデータを与えるからである。これらを r1, r2 及び r3で表すと、 r1 と r2の差はNewtonの補間公式のおよその剰余項であり、r1 と r3の差は手順[3]により1回修正された剰余項である。解が4次より低次の多項式であるか区分幅hに依存して無視し得る剰余項を持つ場合を除いて手順[3]をこれ以上繰り返すのは演算子法の理論上意味がない。故に、r2 と r3の差は最初に近似された剰余項の誤差であるといえる。もしこれが無視できないなら区分幅hは適当ではない。従って、適当な区分幅は次に示す手順により見積もられる。
(1). .|r2−r3| が無視できないならステップ幅hを半分にする。
(2). .|r2−r3| が無視できるなら収束である。そして
(3). .|r1−r3| が無視できて、偶数番目のステップなら次の2ステップを1ステップに結合する、
. . .従って、ステップ幅は直前の2倍になる。
| Program 2.2 |
|---|
|
10 DIM Y0(6),Y1(6),Y2(6),Y(6):DEFINT E,J 12 DEF FNY1=(5*Y0(J3+1)+8*Y1(J3+1)-Y2(J3+1))*H3+ . . Y0(J3):DEF FNY2=(Y0(J3+1)+4*Y1(J3+1)+Y2(J3+1)) . . *H4+Y0(J3) 14 RP=16777216#:RM=2/RP 16 GOSUB 58:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE; . . " N=";N;" H=";H0:N1=ND+1 18 EE=1:XL=XB:X=XB:GOSUB 48:FOR IB=1 TO N:ES=1: . . XI=XL:XL=XB+H0*IB:X0=XI 20 WHILE 2:H1=H0/EE:EB=ES:WHILE EB=<EE: . . X2=XI+H1*EB:IF EB=EE THEN X2=XL 22 LOCATE 0,CSRLIN:PRINT"IB=";IB;" EB=";EB; . . " EE=";EE;" X=";X2;:GOSUB 46 24 FOR J3=1 TO ND:Y1(J3)=Y0(J3+1)*H+Y0(J3): . . Y(J3)=Y1(J3):NEXT:GOSUB 50 26 FOR J3=1 TO ND:Y1(J3)=(Y0(J3+1)+Y1(J3+1))*H* . . .5+Y0(J3):Y2(J3)=Y1(J3+1)*H2+Y0(J3): . . Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52 28 IF ABS(Y2(ND))<1 THEN RA=RP ELSE RA=1 30 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2: . . Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52 32 R1=Y(ND)*RA 34 FOR J3=ND TO 1 STEP-1:Y1(J3)=FNY1:Y2(J3)=FNY2 . . :Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52 36 R2=Y(ND)*RA:J3=ND:Y2(J3)=FNY2:Y(J3)=Y2(J3): . . R3=Y(ND)*RA 38 RA=RM*ABS(R3):IF ABS(R2-R3)<RA THEN . . GOSUB 54:X=X2:GOSUB 48:X0=X2:GOSUB 42 ELSE . . IF EE<&H4000 THEN EE=EE*2:ES=EB*2-1:EB=EE+1 . . ELSE PRINT"EE>&h4000":END 40 EB=EB+1:WEND:IF EB>EE+1 THEN WEND ELSE . . NEXT IB:END 42 IF ABS(R1-R3)<RA THEN IF EE>1 AND(EB MOD 2=0) . . THEN EE=EE\2:ES=EB\2+1:IF ES=<EE THEN EB=EE+1 44 RETURN 46 H2=X2-X0:H=H1*.5:H3=H/12:H4=H2/6:X1=X0+H: . . RETURN 48 GOSUB 56:Y0(N1)=F:FOR J3=1 TO ND:Y0(J3)=Y(J3) . . :NEXT:RETURN 50 X=X1:GOSUB 56:Y1(N1)=F:RETURN 52 X=X2:FOR J3=1 TO ND:Y(J3)=Y2(J3):NEXT: . . GOSUB 56:Y2(N1)=F:RETURN 54 X#=X2:GOSUB 60:YY#=Y(1):LOCATE 40,CSRLIN:PRINT . . USING"Y=##.#######^^^^ True=##.########^^^^"; . . YY#;Y#:RETURN
56 F=100*(SIN(X)-Y(1)):RETURN N=the number of equidistances between XB to XE. |
. .
上記の手順(3)で偶数番目のステップのとき、次の2ステップを結合する理由は二つある。その一つは2分割される前のステップ幅を正確に復元するためである。もう一つはある一区間で分割と結合を2安定的に繰り返すのを防ぐためである。
. .
n階の微分方程式の場合には、r1, r2 及び r3は3回繰り返されるy(n−1)の値である。その他のy(n−2) から y 迄の値は
. .
Program 2.2 はBASICによる可変ピッチ解法を示す。38行は上記手順の(1)と(2)であり、42行は手順(3)である。28行は、(1.2)の手順[2]において |y2|<1 の場合に、r1, r2 及び r3の差の計算で指数部のアンダーフローを避けるためにこれらを 224倍する。20行の"WHILE 2"は無限繰返しであり、この繰返しは40行の"ELSE"で終わる。
. .
56行と58行は(1.16)の微分方程式を解くための副プログラムであり、Table 2.4 は解の一部を示す。基本ステップ間隔は等間隔であり、全積分範囲[0,50]を500に区分することを指定しているから2h=0.1 より大きくはならない。これら等間隔点における解のみを必要とするなら54行の先頭に"IF EB<EE THEN RETURN ELSE "を付ければよい。
2.4 可変刻み3分点法の数値解
| Table 2.4 Solution of y' =100(sin t −y), y(0)=0 by the variable pitch method. | ||||||
|---|---|---|---|---|---|---|
| IB | EB | EE | t (10n) | y | Accurate y | 10n |
| 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 |
1 2 3 14 8 24 13 32 17 15 16 1 2 5 10 6 16 |
512 512 512 512 256 256 128 128 64 16 16 16 16 32 32 16 16 |
1.95312(-4) 3.90625(-4) 5.85937(-4) 2.73438(-3) 0.003125 0.009375 0.0101563 0.025 0.0265625 0.09375 0.1 0.10625 0.1125 0.115625 0.13125 0.1375 0.2 |
1.8949914 7.5310159 1.6835715 3.4197359 4.4115592 3.2910295 3.7779736 1.5819790 1.7263290 8.3649129 8.9874841 9.6097231 1.0231596 1.0542386 1.2094744 1.2714882 1.8884976 |
1.89499145 7.53101618 1.68357167 3.41973592 4.41155928 3.29102951 3.77797369 1.58197891 1.72632887 8.36491276 8.98748430 9.60972308 1.02315963 1.05423863 1.20947437 1.27148822 1.88849783 |
-6 -6 -5 -4 -4 -3 -3 -2 -2 -2 -2 -2 -1 -1 -1 -1 -1 |
. . 微分方程式(2.4)も硬い微分方程式であり条件 h<0.000998を必要とする。しかし、t=0 の近傍で単精度の正確な解を得るためにはこの条件は十分ではなく、十分な条件は得られない。Program 2.2 はその条件を使用せずに、区間幅 0.1 による解を要求する次の副プログラムを使用して正確な解を得ることができる。Table 2.5 と 2.6 はその結果を示す。
| y" +1001y' +1000y=0, | y1(0)=1, y1' (0)=998, | y2(0)=0, y2' (0)=−999 | (2.4) |
| 56 F=-1001*Y(2)-1000*Y(1):RETURN 58 XB=0:XE=5:N=50:ND=2:Y(2)=998:Y(1)=1:RETURN 60 Y#=2*EXP(-X#)-EXP(-1000*X#):RETURN | :' For y2 :' Y(2)=-999:Y(1)=0 :' Y#=-EXP(-X#)+EXP(-1000*X#) | ||
. . 上記副プログラムの58行はこの微分方程式をステップ間隔 2h=0.1 で解くことを要求しているけれども、この区間幅では解は収束しない。このステップ区間が1024に分割されたとき、t=0.1/1024 において最初に解が収束する。21番目のステップは収束しないので2分割される。その最初のステップは 2048 ステップ中の41番目のステップとなる。 127 番目のステップは収束しないので2分割される。その最初のステップは 4096 ステップ中の 253 番目のステップとなる。 4096 ステップ中の 260 番目のステップの後、 2048 ステップ中の 148 番目のステップの後、 1024 ステップ中の 104 番目のステップの後等々においてステップ区間は結合されて直前の区間の2倍となる。このようにして、ステップ間隔は t=0.1 の近傍及びそれ以降では約 0.1/64 となる。Table 2.6 は解 y2が同様にして得られることを示す。
|
| ||||||||||||||||||||||||||||||||||||||||||
| Table 2.7 y' =−ty, y(0)=10, basic H=0.1 | ||||||
|---|---|---|---|---|---|---|
| IB | EB | EE | t | y | Accurate | 10n |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 50 60 70 80 90 100 110 120 130 |
1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 4 4 4 8 8 8 8 8 16 16 16 16 16 |
1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 4 4 4 8 8 8 8 8 16 16 16 16 16 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.5 3.0 3.5 4.0 5.0 6.0 7.0 8.0 9.0 10.0 11.0 12.0 13.0 |
9.9501247 9.8019867 9.5599747 9.2311630 8.8249683 8.3527012 7.8270445 7.2614894 6.6697669 6.0653052 5.4607425 4.8675208 4.2955723 3.7531102 3.2465239 2.7803721 2.3574600 1.9789861 1.6447442 1.3533524 4.3936917 1.1108992 2.1874905 3.3546255 3.7266538 1.5229992 2.2897394 1.2664200 2.5767636 1.9287552 5.3111059 5.3802019 2.0050166 |
9.95012479 9.80198673 9.55997478 9.23116344 8.82496903 8.35270199 7.82704545 7.26149030 6.66976789 6.06530660 5.46074412 4.86752228 4.29557318 3.75311111 3.24652467 2.78037290 2.35746057 1.97898674 1.64474464 1.35335283 4.39369336 1.11089965 2.18749112 3.35462628 3.72665317 1.52299797 2.28973485 1.26641655 2.57675711 1.92874985 5.31109225 5.38018616 2.00500878 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -01 -01 -02 -03 -05 -07 -10 -13 -17 -21 -26 -31 -36 |
. . このように、この解法は区間幅hの条件を見積もることなしに安定にして正確な解を得る。しかし、解がインパルス応答より速やかに減衰する場合及び緩やかに増加する場合は、従来の解法と同様に、零から遠く離れた点までの範囲に渡って解を得ることはできない。
2.5 可変刻み5分点法
. .
著者の5分点解法は(2.1)に示されており、手順[5]のy4は3回修正される。これらの値をr1, r2, r3で表せば、解の収束及び適当な区分幅hは可変刻み3分点法と同様な方法で決定される。
|
[1] |r2−r3| が無視できないなら、ステップ幅 4h を2分割する。 [2] |r2−r3| が無視できるなら解は収束である。そのとき、 [3] |r1−r3| が無視できて、偶数番目のステップなら、次の2ステップを結合する。 . .従って、ステップ幅は直前のステップ幅の2倍になる。 |
. .
従って、可変刻み幅のプログラムは Program 2.2 にある繰り返し文を Program 2.1 に付け加えることにより構成される。そのプログラムは Program 2.3 に示されている。収束の条件は繰り返された値の差が零から最小位2bit迄の違いであることであり、二つのステップ区間を結合する条件はその差が零から最小位bitの違いであることである。これらの条件は多くの試行の結果決定された。
. .
66行と68行は与えられた微分方程式を解くための副プログラムである。基本ステップ幅は等間隔であり、全範囲[0, 13]を130に分割することが要求されているから、基本ステップ幅は 4h=0.1 より大きくはならない。これらの等間隔点における解のみが必要なら64行の先頭に"IF EB<EE THEN RETURN ELSE "を付け加えればよい。
| Program 2.3 |
|---|
|
10 DIM Y0(6),Y1(6),Y2(6),Y3(6),Y4(6),Y(6):DEFINT E,J 12 DEF FNY1=(5*Y0(J3+1)+8*Y1(J3+1)-Y2(J3+1))*H3+Y0(J3): DEF FNY2=(Y0(J3+1)+4* . . Y1(J3+1)+Y2(J3+1))*H4+Y0(J3): DEF FNY3=(Y0(J3+1)+3*Y2(J3+1))*H5+Y0(J3) 14 DEF FNY4=(9*Y0(J3+1)+19*Y1(J3+1)-5*Y2(J3+1)+Y3(J3+1))*H6+Y0(J3): . . DEF FNY6=(Y0(J3+1)+3*Y1(J3+1)+3*Y2(J3+1)+Y3(J3+1))*H8+Y0(J3): . . DEF FNY7=(2*Y1(J3+1)-Y2(J3+1)+2*Y3(J3+1))*H9+Y0(J3):'fny5=fny2 16 DEF FNY8=(251*Y0(J3+1)+646*Y1(J3+1)-264*Y2(J3+1)+106*Y3(J3+1)-19*Y4(J3+1))* . . H10+Y0(J3): DEF FNY9=(29*Y0(J3+1)+124*Y1(J3+1)+24*Y2(J3+1)+4*Y3(J3+1)- . . Y4(J3+1))*H11+Y0(J3): DEF FNY10=(9*Y0(J3+1)+34*Y1(J3+1)+24*Y2(J3+1)+14* . . Y3(J3+1)-Y4(J3+1))*H12+Y0(J3) 18 DEF FNY11=(7*Y0(J3+1)+32*Y1(J3+1)+12*Y2(J3+1)+32*Y3(J3+1)+7*Y4(J3+1))*H13+ . . Y0(J3):RP=16777216#:RM=4/RP 20 GOSUB 68:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE;" N=";N;" H=";H0:N1=ND+1 22 EE=1:XL=XB:X=XB:GOSUB 54:FOR IB=1 TO N:ES=1:XI=XL:XL=XB+H0*IB:X0=XI 24 WHILE 2:HE=H0/EE:EB=ES:WHILE EB=<EE:X4=XI+HE*EB:IF EB=EE THEN X4=XL 26 LOCATE 0,CSRLIN:PRINT"IB=";IB;" EB=";EB;" EE=";EE;" X=";X4;:GOSUB 52 28 FOR J3=1 TO ND:Y1(J3)=Y0(J3+1)*H+Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 56 30 FOR J3=1 TO ND:Y1(J3)=(Y0(J3+1)+Y1(J3+1))*H*.5+Y0(J3):Y2(J3)=Y1(J3+1)*H2+ . . Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 56:GOSUB 58 32 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:Y3(J3)=FNY3:Y(J3)=Y1(J3):NEXT: . . GOSUB 56:GOSUB 58:GOSUB 60 34 FOR J3=1 TO ND:Y1(J3)=FNY4:Y2(J3)=FNY2:Y3(J3)=FNY6:Y4(J3)=FNY7:Y(J3)=Y1(J3) . . :NEXT:GOSUB 56:GOSUB 58:GOSUB 60:GOSUB 62 36 IF ABS(Y4(ND))<1 THEN RA=RP ELSE RA=1 38 FOR J3=1 TO ND:Y1(J3)=FNY8:Y2(J3)=FNY9:Y3(J3)=FNY10:Y4(J3)=FNY11:Y(J3)= . . Y1(J3):NEXT:GOSUB 56:GOSUB 58:GOSUB 60:GOSUB 62:R1=Y(ND)*RA 40 FOR J3=ND TO 1 STEP-1:Y1(J3)=FNY8:Y2(J3)=FNY9:Y3(J3)=FNY10:Y4(J3)=FNY11: . . Y(J3)=Y1(J3):NEXT:GOSUB 56:GOSUB 58:GOSUB 60:GOSUB 62:R2=Y(ND)*RA 42 J3=ND:Y4(J3)=FNY11:Y(J3)=Y4(J3):R3=Y(ND)*RA:RA=RM*ABS(R3) 44 IF ABS(R2-R3)<RA THEN GOSUB 64:X=X4:GOSUB 54:X0=X4:GOSUB 48 ELSE . . IF EE<&H4000 THEN EE=EE*2:ES=EB*2-1:EB=EE+1 ELSE PRINT"EE>&h4000":END 46 EB=EB+1:WEND:IF EB>EE+1 THEN WEND ELSE NEXT IB:END 48 IF ABS(R1-R3)*2<RA THEN IF EE>1 AND(EB MOD 2=0)THEN EE=EE\2:ES=EB\2+1: . . IF ES=<EE THEN EB=EE+1 50 RETURN 52 HM=X4-X0:H=HE*.25:H2=HE*.5:H1=HE*.75:H3=H/12:H4=H2/6:H5=H1/4:H6=H/24: . . H8=H1/8:H9=HM/3:H10=H/720:H11=H/90:H12=H1/80:H13=HM/90:X1=X0+H:X2=X0+H2: . . X3=X0+H1:RETURN 54 GOSUB 66:Y0(N1)=F:FOR J3=1 TO ND:Y0(J3)=Y(J3):NEXT:RETURN 56 X=X1:GOSUB 66:Y1(N1)=F:RETURN 58 X=X2:FOR J3=1 TO ND:Y(J3)=Y2(J3):NEXT:GOSUB 66:Y2(N1)=F:RETURN 60 X=X3:FOR J3=1 TO ND:Y(J3)=Y3(J3):NEXT:GOSUB 66:Y3(N1)=F:RETURN 62 X=X4:FOR J3=1 TO ND:Y(J3)=Y4(J3):NEXT:GOSUB 66:Y4(N1)=F:RETURN 64 X#=X4:GOSUB 70:YY#=Y(1):LOCATE 40,CSRLIN:PRINT USING . . "Y=##.#######^^^^ True=##.########^^^^";YY#;Y#:RETURN
66 F=-X*Y(1):RETURN |
2.6 可変刻み5分点法の数値解
. .
上記の副プログラムで与えられた微分方程式の解は Table 2.8 に示されている。同表には精度の比較のために3分点法の解も載せられている。解の値には違いはないけれども与えられた区分幅の細分割数が少ない点で5分点法が優れている。5分点法はステップ幅 4h であるが、3分点法はステップ幅 2h である。従って、ステップ幅が3分点法の2倍であれば両解法は同じhの値となる。しかし、同表は5分点法のステップ幅は t=3.0 より大きなtの辺りでは3分点法のステップ幅の4倍になることを示している。これは5分点法が3分点法より精度が良いことを示してる。
| Table 2.8. . y' = −ty, y(0)=10, basic H=0.1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 points method | 3 points method | |||||||||||
| IB | EB | EE | t | y | Accurate y | exp | IB | EB | EE | t | y | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 50 60 70 80 90 100 110 120 130 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 4 4 4 4 4 4 8 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 4 4 4 4 4 4 8 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.5 3.0 3.5 4.0 5.0 6.0 7.0 8.0 9.0 10.0 11.0 12.0 13.0 |
9.9501247 9.8019867 9.5599747 9.2311630 8.8249683 8.3527012 7.8270445 7.2614894 6.6697669 6.0653057 5.4607434 4.8675218 4.2955728 3.7531106 3.2465243 2.7803726 2.3574603 1.9789865 1.6447445 1.3533527 4.3936929 1.1108997 2.1874912 3.3546258 3.7266531 1.5229985 2.2897369 1.2664183 2.5767609 1.9287527 5.3111016 5.3801972 2.0050135 |
9.95012479 9.80198673 9.55997478 9.23116344 8.82496903 8.35270199 7.82704545 7.26149030 6.66976789 6.06530660 5.46074412 4.86752228 4.29557318 3.75311111 3.24652467 2.78037290 2.35746057 1.97898674 1.64474464 1.35335283 4.39369336 1.11089965 2.18749112 3.35462628 3.72665317 1.52299797 2.28973485 1.26641655 2.57675711 1.92874985 5.31109225 5.38018616 2.00500878 |
+00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 -01 -01 -02 -03 -05 -07 -10 -13 -17 -21 -26 -31 -36 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 50 60 70 80 90 100 110 120 130 |
1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 4 4 4 8 8 8 8 8 16 16 16 16 16 |
1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 4 4 4 8 8 8 8 8 16 16 16 16 16 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.5 3.0 3.5 4.0 5.0 6.0 7.0 8.0 9.0 10.0 11.0 12.0 13.0 |
9.9501247 9.8019867 9.5599747 9.2311630 8.8249683 8.3527012 7.8270445 7.2614894 6.6697669 6.0653052 5.4607425 4.8675208 4.2955723 3.7531102 3.2465239 2.7803721 2.3574600 1.9789861 1.6447442 1.3533524 4.3936917 1.1108992 2.1874905 3.3546255 3.7266538 1.5229992 2.2897394 1.2664200 2.5767636 1.9287552 5.3111059 5.3802019 2.0050166 | |
. . Table 2.9 は次の副プログラムで示される硬い微分方程式の解を示す。この場合は、5分点法のステップ幅は t=0 の近傍では3分点法のステップ幅の8倍ある。これは、硬い微分方程式はより大きな区分幅hで解きたいなら高次解法で解かねばならないことを示す。但し、hは第1.5節で述べた解の存在条件を満たしていなければならない。
. . 第2.2節で述べた固定刻み幅解法の場合には5分点法は3分点法より僅かに解の精度が悪かった。その理由はhの値が大きく、解の存在のための臨界条件に近かったことにある。Table 2.9 はhの値がもっと小さく、約 0.1/64 であれば、5分点法の解の精度が3分点法より良いことを示す。
|
66 F=100*(SIN(X)-Y(1)):RETURN 68 XB=0:XE=50:N=500:ND=1:Y(1)=0:RETURN 70 Y#=(SIN(X#)-.01#*(COS(X#)-EXP(-100*X#)))/1.0001#:RETURN |
| Table 2.9 . .Solution of . .y' =100(sin t −y), y(0)=0, basic H=0.1. | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 points method | 3 points method | ||||||||||||
| IB | EB | EE | t | y | Accurate y | exp | IB | EB | EE | t(10n) | y | exp | |
| 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 4 5 6 7 8 9 10 |
1 2 3 4 3 4 5 6 7 8 9 10 6 7 8 9 10 6 7 8 1 2 3 4 5 6 7 8 8 8 8 8 8 8 8 8 |
64 64 64 64 32 32 32 32 32 32 32 32 16 16 16 16 16 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 |
0.0015625 0.003125 0.0046875 0.00625 0.009375 0.0125 0.015625 0.01875 0.021875 0.025 0.028125 0.03125 0.0375 0.04375 0.05 0.05625 0.0625 0.075 0.0875 0.1 0.1125 0.125 0.1375 0.15 0.1625 0.175 0.1875 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 |
1.1595325 4.4115595 9.4533840 1.6026088 3.2910297 5.3649675 7.7209268 1.0283181 1.2996316 1.5819788 1.8723922 2.1686995 2.7730646 3.3868104 4.0055037 4.6267595 5.2492894 6.4956851 7.7420481 8.9874841 1.0231596 1.1474132 1.2714882 1.3953647 1.5190233 1.6424446 1.7656091 1.8884978 2.8593826 3.8016972 4.7060263 5.5633348 6.3650554 7.1031797 7.7703309 8.3598429 |
1.15953252 4.41155928 9.45338329 1.60260869 3.29102951 5.36496733 7.72092668 1.02831811 1.29963169 1.58197891 1.87239224 2.16869970 2.77306478 3.38681073 4.00550414 4.62675988 5.24928980 6.49568572 7.74204870 8.98748430 1.02315963 1.14741320 1.27148822 1.39536477 1.51902335 1.64244460 1.76560908 1.88849783 2.85938259 3.80169721 4.70602653 5.56333504 6.36505606 7.10318000 7.77033129 8.35984363 |
-04 -04 -04 -03 -03 -03 -03 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 4 5 6 7 8 9 10 |
1 2 3 14 8 24 13 24 28 32 18 20 24 28 16 18 20 12 14 16 2 8 6 8 10 12 14 16 32 32 32 16 16 32 32 16 |
512 512 512 512 256 256 128 128 128 128 64 64 64 64 32 32 32 16 16 16 16 32 16 16 16 16 16 16 32 32 32 16 16 32 32 16 |
1.953(-4) 3.906(-4) 5.859(-4) 2.734(-3) 0.003125 0.009375 0.0101563 0.01875 0.021875 0.025 0.028125 0.03125 0.0375 0.04375 0.05 0.05625 0.0625 0.075 0.0875 0.1 0.1125 0.125 0.1375 0.15 0.1625 0.175 0.1875 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 |
1.8949914 7.5310159 1.6835715 3.4197359 4.4115592 3.2910295 3.7779736 1.0283181 1.2996317 1.5819790 1.8723924 2.1686997 2.7730649 3.3868108 4.0055040 4.6267599 5.2492898 6.4956859 7.7420488 8.9874841 1.0231596 1.1474132 1.2714882 1.3953647 1.5190233 1.6424444 1.7656089 1.8884976 2.8593826 3.8016969 4.7060263 5.5633348 6.3650554 7.1031797 7.7703309 8.3598435 |
-06 -06 -05 -04 -04 -03 -03 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 | |
. .
Table 2.10 は次の副プログラムに示される硬い微分方程式の解を示す。この場合にも、5分点法は t=0 の辺りでは3分点法の8倍のステップ幅である。これも又、硬い微分方程式をより大きな区分幅hで解きたいなら高次解法で解かねばならないことを示す。
. .
これらの例は数値解法は常に固定区分幅の固定次数解法を使用したいという考えは正しくないことを示す。それは可変区分幅の可変次数多項式を用いる方法であるべきである。著者の演算子法はそのような解法を導くことができ、それは後で示す。
|
66 F=-1001*Y(2)-1000*Y(1):RETURN 68 XB=0:XE=5:N=50:ND=2:Y(1)=1:Y(2)=998:RETURN 70 Y#=2*EXP(-X#)-EXP(-1000*X#):RETURN |
| Table 2.10 . .y" +1001y' +1000y=0, y(0)=1, y' (0)=998, basic H=0.1. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 points method | 3 points method | |||||||||||
| IB | EB | EE | t(10n) | y | Accurate y | exp | IB | EB | EE | t(10n) | y | |
| 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
1 2 3 4 5 36 19 30 16 22 12 16 9 14 29 32 32 32 32 64 64 64 32 64 64 64 64 32 32 32 32 32 32 32 32 64 |
512 512 512 512 512 512 256 256 128 128 64 64 32 32 64 64 32 32 32 64 64 64 32 64 64 64 64 32 32 32 32 32 32 32 32 64 |
1.953(-4) 3.906(-4) 5.859(-4) 7.812(-4) 9.765(-4) 7.031(-3) 7.421(-3) 0.0117188 0.0125 0.0171875 0.01875 0.025 0.028125 0.04375 0.0453125 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
1.1770319 1.3225851 1.4422448 1.5406048 1.6214445 1.9851032 1.9846134 1.9766912 1.9751520 1.9659189 1.9628496 1.9506202 1.9445339 1.9143869 1.9113979 1.9024594 1.8096752 1.6374617 1.4816371 1.3406409 1.2130620 1.0976241 9.9317122 8.9865839 8.1313986 7.3575944 6.6574264 6.0238880 5.4506403 4.9319440 4.4626072 4.0379336 3.6536735 3.3059800 2.9913747 2.7067077 |
1.17703185 1.32258506 1.44224466 1.54060475 1.62144438 1.98510300 1.98461317 1.97669115 1.97515187 1.96591869 1.96284937 1.95061982 1.94453365 1.91438645 1.91139756 1.90245885 1.80967483 1.63746150 1.48163642 1.34064008 1.21306132 1.09762325 9.93170619 8.98657918 8.13139290 7.35758882 6.65742152 6.02388395 5.45063547 4.93193940 4.46260320 4.03793026 3.65367031 3.30597753 2.99137246 2.70670566 |
+00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 +00 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 -01 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
1 41 253 131 148 75 76 60 64 44 24 16 18 14 15 32 64 32 128 16 64 64 64 64 64 64 32 64 32 64 128 64 64 64 64 64 |
1024 2048 4096 2048 2048 1024 1024 512 512 256 128 64 64 32 32 64 64 32 128 16 64 64 64 64 64 64 32 64 32 64 128 64 64 64 64 64 |
9.765(-5) 2.001(-3) 6.176(-3) 6.396(-3) 7.226(-3) 7.324(-3) 7.421(-3) 0.0117188 0.0125 0.0171875 0.01875 0.025 0.028125 0.04375 0.046875 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 |
1.0928441 1.8609290 1.9856073 1.9855803 1.9848721 1.9847459 1.9846133 1.9766912 1.9751519 1.9659187 1.9628493 1.9506197 1.9445336 1.9143865 1.9084134 1.9024590 1.8096751 1.6374615 1.4816370 1.3406407 1.2130615 1.0976236 9.9317110 8.9865828 8.1313980 7.3575932 6.6574252 6.0238856 5.4506361 4.9319416 4.4626060 4.0379316 3.6536717 3.3059785 2.9913738 2.7067062 | |
次 2.7 微分方程式の数値解法による定積分 へ