1. 常微分方程式の新しい数値解法
1.1 演算子法の概略
. .
等間隔変数tk=t0+kh, k=0,1,2,3,.......における関数f(t)の値がf0, f1, f2, f3, ........であるとき、関数f(t)はニュートンの補間公式で表され、等間隔変数tkに対する積分値ykはスターリングの積分公式で表される。従って、ykの階差はfkの階差を用いた公式で表される。その公式は行列を用いた数式で(1.1)のように記述できる。公式の行列は上部三角行列であり、第i行は第i−1行を1列右に移して第1列に0をセットした構造を持つ。その第1行は次のようになる。
1.2 常微分方程式の数値解法
. .
微分方程式y' =f(y, t)及び初期値y0が与えられたとき、(1.1)式の1行1列の部分行列を用いてΔy0を予測する。次に、2行2列の部分行列とf(y, t)により求められたΔf0を用いてΔy0を修正し、Δ2y0を予測する。最後に、2行3列の行列とf(y, t)により修正されたΔf0とΔ2f0を用いてΔy0とΔ2y0を数回修正する。次に、初期値点をt2に移して同じ操作を繰り返す。
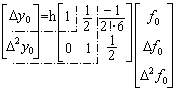 | (1.1) |
. . 全積分範囲をn区間に等分割し、その1区間を更に2等分するとき、(1.1)の解法をn回繰り返せば全積分範囲の解が得られる。この方法は、Runge-Kuttaより精度がよく、以下に示すような簡単にして新しい解法を導く。ここより、変数tは実数を、xはそれをある精度に丸めた値を取るものとする。
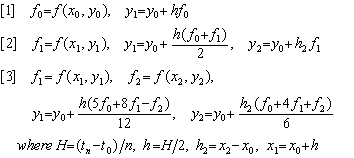 | (1.2) |
. . 関数z(t)により駆動されるn階の常微分方程式を解く方法は二通りある。その一つは微分行列Dの多項式を計算して得た行列の逆行列を計算しなければならないのでやや複雑である。もう一つは微分方程式が(1.3)で表せるので(1.2)の解法をn回繰り返せばよく、簡単である。
| (1.3) |
. . 従来の解法は簡単な変数置換により(1.3)の第1式をn個の1階の微分方程式からなる連立方程式に変換する。それは(1.3)の変数yからy(n−1)のそれぞれに変数y1からynを代入した式で表される。その解法はそれら1階の微分方程式を順に積分するのであり、著者の解法と同じになるが、著者の解法は変数置換を必要とせず、(1.3)の第1式を与えるだけでよい。その理由は第2式以降は全ての微分方程式に共通だからである。
1.3 プログラムと実行結果
. .
著者の解法はBASICによりProgram 1 のように書くことが出来る。これは配列のサイズを6に設定しているので1階から5階迄の微分方程式を解くことが出来る。プログラムは行番号56と58に副プログラムを与えなければならない。前者は(1.3)の第1式の右辺を与え、後者は、全積分範囲、等間隔区分数、微分方程式の階数、及び、初期値を与える。行番号60は計算結果を比較するための真値を与える。しかし、行番号54の"X#=X2:GOSUB 60"及び変数Y#と共に削除することが出来る。解の値は末尾に単精度長の0を付加して2倍長の2進数に変換した後8桁の浮動少数に10進化している。
| Program 1 |
|---|
|
10 DIM Y0(6),Y1(6),Y2(6),Y(6):DEFINT E,J 12 DEF FNY1=(5*Y0(J3+1)+8*Y1(J3+1)-Y2(J3+1))*H3+ . . Y0(J3):DEF FNY2=(Y0(J3+1)+4*Y1(J3+1)+Y2(J3+1)) . . *H4+Y0(J3) 16 GOSUB 58:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE; . . " N=";N;" H=";H0:N1=ND+1 18 X2=XB:FOR IB=1 TO N:X0=X2:X2=XB+H0*IB:X=X0: . . GOSUB 48 22 LOCATE 0,CSRLIN:PRINT"IB=";IB;" X=";X2;: . . GOSUB 46 24 FOR J3=1 TO ND:Y1(J3)=Y0(J3+1)*H+Y0(J3): . . Y(J3)=Y1(J3):NEXT:GOSUB 50 26 FOR J3=1 TO ND:Y1(J3)=(Y0(J3+1)+Y1(J3+1))*H* . . .5+Y0(J3):Y2(J3)=Y1(J3+1)*H2+Y0(J3): . . Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52 30 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2: . . Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52 34 FOR J3=ND TO 1 STEP-1:Y1(J3)=FNY1:Y2(J3)=FNY2 . . :Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52 36 J3=ND:Y2(J3)=FNY2:Y(J3)=Y2(J3) 40 GOSUB 54:NEXT IB:END 46 H2=X2-X0:H=H0*.5:H3=H/12:H4=H2/6:X1=X0+H: . . RETURN 48 GOSUB 56:Y0(N1)=F:FOR J3=1 TO ND:Y0(J3)=Y(J3) . . :NEXT:RETURN 50 X=X1:GOSUB 56:Y1(N1)=F:RETURN 52 X=X2:FOR J3=1 TO ND:Y(J3)=Y2(J3):NEXT: . . GOSUB 56:Y2(N1)=F:RETURN 54 X#=X2:GOSUB 60:YY#=Y(1):LOCATE 40,CSRLIN:PRINT . . USING"Y=##.#######^^^^ True=##.########^^^^"; . . YY#;Y#:RETURN 56 F=-2*Y(1)-2*Y(2):RETURN 58 XB=0:XE=90:N=900:ND=2:Y(1)=0:Y(2)=1:RETURN 60 Y#=EXP(-X#)*SIN(X#):RETURN [Note] Y(k+1)=y(k), ND=n-th order. . . N=the number of equidistances between XB to XE. |
. . Program 1 は(1.4)を解くための副プログラムと等間隔区分長2h=0.1が与えられている。Table 1 は解の一部をRunge-Kutta法の解と共に示す。著者の解法の解はテーブルに示すようにRunge-Kutta法の解より約1桁精度がよい。その理由は以下に示すように幾つかある。
| Table 1. The solutions of Eq.(1.4). | ||||
|---|---|---|---|---|
| t | Author | Runge-K | True value | Exp |
| 0.1 0.2 0.3 0.4 2.0 3.0 4.0 10.0 20.0 30.0 40.0 83.0 84.0 85.0 |
9.0333059 1.6265677 2.1892685 2.6103503 1.2305982 7.0258616 −1.3861313 −2.4698591 1.8817083 −9.2454568 3.1653754 8.7012940 2.4258100 −2.1319470 |
9.0333343 1.6265723 2.1892738 2.6103556 1.2305877 7.0253122 −1.3861323 −2.4699193 1.8816610 −9.2445311 3.1646361 8.6687695 2.4146370 −2.1310768 |
9.03330122 1.62656693 2.18926760 2.61034923 1.23060025 7.02595149 −1.38613212 −2.46985202 1.88172041 −9.24562742 3.16550467 8.70155450 2.42370770 −2.14125438 |
−02 −01 −01 −01 −01 −03 −02 −05 −09 −14 −18 −37 −37 −38 |
1.4 数値解の精度
. .
1積分区間の2分の1をhで表すとき微分方程式(1.4)の解は手順[1][2][3]及び[3]により級数に展開され、x=2hにおいて(1.5)で表される。Runge-Kutta法の解も同様に級数に展開されるが最後の項が存在しない。最後の項の分母はTaylor展開では30である。Table 1 はこれら三者の関係を示している。
| (1.5) |
. . Runge-Kutta法は1積分区間の中点に対してx1, f1, y1及び区間幅hを用い、積分区間の端に対してx2, f2, y2及び区間幅2hを用いると次のように記述できる。
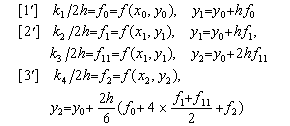 | (1.6) |
. . 例えば、dy/dt =−y, y(0)=1の解は4次のTaylor展開に展開されるが、もう一度手順[3']を繰り返しても何の違いも得られない。その理由は、k4が中点における関数fの値にのみ依存するy0+k3により決定されるからである。しかし、手順[3']のようにy2でy0+k3を置き換えるなら、それは(1.6)に示すようにx=2hに対して予測した値でもよいから繰返しにより2hの5乗の項が生ずるが正しくない。更に、4乗の項が正しくないものに変わってしまう。そして、数値計算結果はTable 2 に2h=0.2の場合を示すが精度が悪くなる。
| Table 2. The results repeated [3] and [3'] | ||||
|---|---|---|---|---|
| Author's method | Runge-Kutta | True | ||
| 1×[3] 2×[3] 3×[3] | 0.8186667 0.8187333 0.8187311 | 1×[3'] 2×[3'] 3×[3'] | 0.8187333 0.8187089 0.8187097 | 0.81873075 |
. . 解が4次以上のTaylor展開で近似されるべきであるとき、例えばdy/dt=y−1, y(0)=0.5, 2h=0.125の場合、著者の解法の解はTable 3 に示すように7次のTaylor展開より約3桁精度がよい。Simpsonの1/3則によるy−1の積分はTaylor展開より約2桁精度がよい。即ち、4次の項がTaylor展開と一致することは重要ではない。3次の項より高次の項の全体を正確に近似することが重要である。従って、数値解法はStirlingの積分公式により導くべきである。
| Table 3. dy/dt=y−1, y(0)=0.5, 2h=0.125 | |||||
|---|---|---|---|---|---|
| t | Author's | Simpson | Runge-K | Taylor(7) | True |
| 0.125 | 0.7071319 | 0.7072122 | 0.7071896 | 0.7106933 | 0.70710678 |
1.5 数値解の存在条件
. .
(1.2)に示した手順[1][2][3][3][3]により得られるy1及びy2の値はそれぞれが微分方程式の解に収束する数列である。それは(1.3)の最初の微分方程式のy(n−1)についても同様である。何故ならその微分方程式はy(n−1)に関する1階の微分方程式と考えてよいからである。故に、その微分方程式の右辺はLipschitzの条件を満たさねばならないがそれだけでは十分ではない。
. .
[定理 1.1]. .積分演算子のノルムは区分幅hに等しい。
[証明]. .t0<ta<tであるtaに対して、f(t)の積分がf(ta)(t−t0)に等しくなるようなtaが存在する。このとき(1.7)を満たすようなある数Mが存在する。
. . 関数f(t)がy(t)の導関数のとき、上に述べた積分は定積分、即ち、y(t0+h)−y(t0)又はy(t0)=0の場合はy(t0+h)である。f(t)がy(t)のn次導関数でk=0からn−1に対してy(k)(t0)=0のとき、区間hの間でf(t)をn重積分する演算子のノルムは次のように導かれる。
. .
[定理 1.2]. .n重積分演算子のノルムはhn/n!である。
[証明]. .f(t)のn重積分は(1.9)の全ての初期値を0にし、y(n)(t)をf(t)に置き換えた式で表される。
| . .(1.9) |
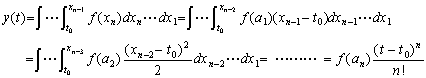
| (1.7)及び(1.8)と同様に、. . |
| . .[証明終] |
. .
微分の定義は下記の第1式で表され、導関数の積分は第2式で表される。何故なら、積分演算はh→0の逆演算を含むべきだからである。故に、積分演算子のノルムは積分区間hである。
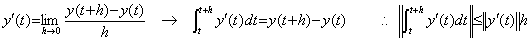
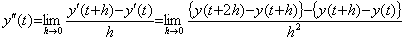
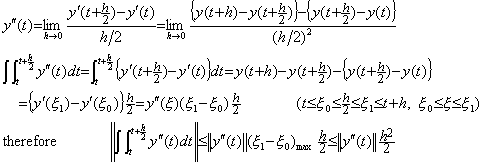
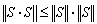 は過大な評価であり、
は過大な評価であり、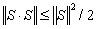 であるべきである。
であるべきである。
. .
[定理 1.3]. .差分法の計算においてはn重積分演算子のノルムはhnである。
[証明]. .Eq.(1.9)のy(n)(t)を置き換えた
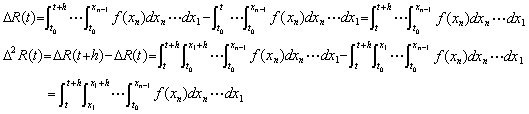
| . .(1.11) | ||
| ∴. .
|
∴. . Minf=hn | [ Q.E.D.] |
. .
差分法においてはEq.(1.10)により、n重積分は n-1次より高次の階差Δmy(t0)を求める。従って、y(t)を求めるためにはn次より低次の階差が初期値の代わりに与えられねばならない。Eq.(1.10)はまた積分毎に積分範囲がhづつ増加することも示している。
. .
被積分関数がf(t)=t3であるとき、これを階差で表すには4点の等間隔点を必要とする。f(t)の積分はもう一点を必要とし、その4hの範囲で積分演算のノルムはhである。従って、0から4h迄の区間のノルムはh×(4h)3=(4h)4/4である。区間が0から3hならノルムは(3h/4)×(3h)3=(3h)4/4である。故に、ノルムの計算は結果が正になることを除いて、関数の計算及び被積分関数に対する積分演算と同様である。
. .
著者の演算子法はこれらを行列の数式表現に明示する。例えば、(1.1)のベクトルFは区間2hを必要とし、2階以上の階差は無視し得ることを必要とする。ベクトルΔYは行列Dの第3行を省略しない表現ではΔ3y0を持つから区間3hを必要とし、行列Dのノルムは1であるから積分のノルムはhである。
. .
[定理 1.4]. .微分方程式(1.3)の解は(1.12)が満たされるとき収束する。
[証明]. .微分方程式がy' =f(y,t), y(t0)=y0であるとき、その解は次式で表される。
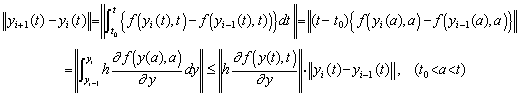 (1.14)
(1.14)(1.13)のyをy(n−1)に置き換えればパラメータy(k)はy(n−1)のn−1−k重積分となり、(1.10)により、
. .
条件式(1.12)にあるtの値は出発点t0であってはならない。その理由は、(1.14)及び、yi(t0)=y(t0)は固定点であることにある。tの値はt0+hでなければならない。関数列yi(t)を構成するため、及び、t0とt0+hの間に極大値が存在しても階差はその値を使用しないからである。
. .
この収束条件はどのような数値解法でも満たされなければならない。例えば、Euler法は最初の近似解をy(t)=y0と仮定してy2(t)を得る。真の解y1(t)とこれら2つの近似解の関係は(1.14)で表され、y2(t)がより良い近似解であるためにはこの収束条件が満たされなければならない。
. .
積分演算子のノルムは使用されている最小の区間幅に等しい。従って、Runge-Kutta法のノルムは刻み幅の半分に等しく、従来行われているP-C法の結果との精度の比較の方法は公正でない。
. .
微分方程式(1.4)を解くプログラムで使用している区分幅h=0.05は(1.12)の条件h(2+2h)<1、即ち、h<0.366を十分に満たしている。微分方程式が(1.15)であるとき、収束条件はh(20−2h)<1、即ち、h<0.05となる。
| y" −20y' +2y=0, | y(0)=0, | y' (0)=1, | (1.15) |
1.6 硬い微分方程式と従来の問題点
. .
微分方程式(1.16)は硬い微分方程式といわれる。これは収束条件100h<1 を持ち、著者の方法ではh=0.01でも精度は極めて悪いが解を得る。しかし、h=0.015では解は得られない。
| y' =100(sin t −y), | y(0)=0 | (1.16) |
| 56 F=100*(SIN(X)-Y(1)):RETURN 58 XB=0:XE=50:N=5000:ND=1:Y(1)=0:RETURN 60 Y#=(SIN(X#)-.01#*(COS(X#)-EXP(-100*X#)))/1.0001#:RETURN |
| Table 4. Solutions of Eq.(1.16), h=0.005 | ||||
|---|---|---|---|---|
| t | author's | Runge-K | True | exp |
|
0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 : 0.96 0.97 0.98 0.99 1.00 1.01 1.02 1.03 : |
3.6805207 1.1354182 2.0496540 3.0177828 4.0055208 5.0001867 5.9970498 6.9943063 7.9912283 8.9874871 9.9828951 1.0977323 1.1970660 1.2962803 1.3953649 : 8.1337517 8.1915098 8.2484484 8.3045620 8.3598453 8.4142929 8.4678990 8.5206574 : |
3.7499631 1.1405773 2.0525275 3.0192034 4.0061768 5.0004739 5.9971679 6.9943488 7.9912379 8.9874804 9.9828817 1.0977305 1.1970639 1.2962779 1.3953625 : 8.1337363 8.1914937 8.2484323 8.3045459 8.3598292 8.4142762 8.4678823 8.5206413 : |
3.67875972 1.13528838 2.04958203 3.01774709 4.00550414 5.00017871 5.99704594 6.99430354 7.99122609 8.98748430 9.98289234 1.09773202 1.19706571 1.29628001 1.39536462 : 8.13375018 8.19150785 8.24844638 8.30456007 8.35984363 8.41429089 8.46789673 8.52065579 : |
-03 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -01 -01 -01 -01 : -01 -01 -01 -01 -01 -01 -01 -01 : |
. .
. . n階の微分方程式は1階の微分方程式n個の連立方程式に置き換えることが出来、その置き換えは可逆である。連立微分方程式(1.18)は硬い微分方程式といわれる。これは2階の微分方程式(1.19)に書き換えてもよい。従って、解の収束条件はh(1001+1000h)<1、即ち、h<0.000998 であり、著者の解法はh=0.001 でも精度は非常に悪いがまだ解が得られる。しかし、h=0.0015では解は得られない
. . 連立微分方程式(1.18)はベクトルと行列の演算式としてY' =AYと表せる。但し、Y' =
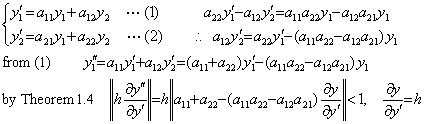
| 56 F=-1001*Y(2)-1000*Y(1):RETURN 58 XB=0:XE=5:N=5000:ND=2:Y(2)=998:Y(1)=1:RETURN 60 Y#=2*EXP(-X#)-EXP(-1000*X#):RETURN | :' For y2 :' Y(2)=-999:Y(1)=0 :' Y#=-EXP(-X#)+EXP(-1000*X#) |
| Table 5. Solutions of Eq.(1.18) and Eq.(1.19), h=0.0005 | |||||||
|---|---|---|---|---|---|---|---|
| t | A's y1 | R-K | True | A's y2 | R-K | True | |
|
.001 .002 .003 .004 .005 .006 .007 .008 .009 .010 .011 .012 .013 .014 .015 : .097 .098 .099 .100 .101 .102 .103 : |
1.6299455 1.8605392 1.9441504 1.9736652 1.9832709 1.9855500 1.9851339 1.9837270 1.9819567 1.9800539 1.9781036 1.9761372 1.9741659 1.9721942 1.9702235 : 1.8151120 1.8132977 1.8114854 1.8096749 1.8078661 1.8060591 1.8042539 : |
1.6230011 1.8553791 1.9412748 1.9722407 1.9826094 1.9852552 1.9850063 1.9836731 1.9819344 1.9800450 1.9781002 1.9761360 1.9741657 1.9721942 1.9702235 : 1.8151116 1.8132974 1.8114851 1.8096745 1.8078657 1.8060588 1.8042536 : |
1.63012158 1.86066873 1.94422194 1.97370034 1.98328701 1.98555718 1.98513700 1.98372837 1.98195735 1.98005427 1.97810385 1.97613728 1.97416601 1.97219426 1.97022357 : 1.81511201 1.81329780 1.81148540 1.80967483 1.80786606 1.80605909 1.80425393 : |
-.63094497 -.86253715 -.94714594 -.97765726 -.98825842 -.99153209 -.99210948 -.99169517 -.99091643 -.99000418 -.98904347 -.98806554 -.98708189 -.98609674 -.98511165 : -.90755606 -.90664893 -.90574276 -.90483749 -.90393311 -.90302962 -.90212703 : |
-.62400055 -.85737705 -.94427019 -.97623265 -.98759675 -.99123716 -.99198174 -.99164099 -.99089390 -.98999500 -.98903978 -.98806411 -.98708141 -.98609662 -.98511159 : -.90755582 -.90664870 -.90574247 -.90483725 -.90393287 -.90302938 -.90212679 : |
-.631121076 -.862666728 -.947217440 -.977692354 -.988274534 -.991539213 -.992112561 -.991696452 -.990916968 -.990004433 -.989043576 -.988065568 -.987081874 -.986096712 -.985111633 : -.907556004 -.906648899 -.905742702 -.904837417 -.903933030 -.903029547 -.902126967 : | |
| (1.20) (1.21) |
. . 微分方程式(1.22)もまたy=0でLipschitz条件を満たさないといわれるが、その点は固定点である。解の収束条件は(1.23)であり、解は(2t)1/2である。従って、出発点t0が区分幅hより非常に大きいなら解は容易に収束するが、t0が零のときはどのような解法もt0における微係数を使用する限り、それは無限大であるから解を得ることはできない。独立変数tをyに換えることが考えられるが、その場合は(1.20)と同様の方法を使わねばならない。
| (1.22) (1.23) |
. . さらに簡単な方法はy=2h/yを解くことっであり、それはt=hにおける正確な解を与える。しかし、次のステップでは殆ど精度を失う。例えば、h=0.1及びy(h)=0.447213が与えられたとき、台形法による解y(2h)は0.637454であるが、正確な値は0.6324555である。著者の解法は0.632478を得、手順[3]を更に繰り返してもhの高次の項が生じ、正しくないので修正されない。更に精度のよい解が必要な場合はt0=0.1より小さな区分幅を使用するか、もっと高次の演算子法の解法が必要である。
1.7 数値解の安定性
. .
数値解の不安定は幾つかの原因による。数値解の収束条件が十分に満たされないのはその原因の一つである。微分方程式(1.24)の数値解の収束条件は(1.25)である。従って、区分幅hは出発点t0が0から遠くなるに従って小さくしなければならない。t0が0に近いなら解の収束条件は(1.26)によりh<tである。これは臨海条件であり、かつ、y' (0)=0であるけれども解は容易に正確に求まる。それはy(0)が零でなく、y(h)もy' (h)も零でないからである。例えば、hが0.1なら1ステップの積分はt=10に近づくに従ってかなりの精度を失うので、全積分範囲が0から10までの場合には終端近傍では近似値が得られないこととなる。
. . (1.27)の微分方程式を微分すると(1.29)の二階の微分方程式が得られる。その解は(1.27)の解と同じであるが、初期値の誤差による応答は非常に異なる。
. . (1.29)の微分方程式の解の第2項は微分初期値の誤差−Aε1によるインパルス応答であり、ε1に漸近する。この微分方程式の解yはインパルス応答ではなく、インパルス応答より速やかに減衰するけれども、Aが整数なら2つの誤差ε0, ε1は略等しく、Ah<1の条件で解は安定に求まる。しかし、Aが整数でないなら、例えば、A=1.3なら解は零へ漸近しない。その理由は、Aの2進値は循環小数であり、その誤差ε1はε0とは異なるからである。初期値がy(0)=0及びy' (0)=−Aであれば、解はインパルス応答e−At−1であるから安定である。
. . (1.27)の微分方程式はA=1 及びA=2の場合とも安定に解ける。しかし、その2つの解を基本解とする微分方程式は正しく解けるとは限らない。(1.30)の解はインパルス応答であり、正しく解けるが、(1.31)の解は初期値の誤差によるインパルス応答にまで減衰した後は正しく解けない。
| y" +3y' +2y=0, | y(0)=0, y' (0)=1 y(0)=1, y' (0)=−2 | then y=e−t−e−2t then y=e−2t | . .(1.30) . .(1.31) |
. . 微分方程式(1.24)を微分すると微分方程式(1.32)を得る。その解は(1.24)の解と同じであるが、数値解は(1.24)のMilne法による解と同じくらい急速に精度を失い、t=5あたりより後はTable 6に示すように安定ではあるが、非常にゆっくりと減衰する。
| Table 7. The solution of y" +ty' +y=δ(t) | |||
|---|---|---|---|
| IB | t | y(exp) | True(exp) |
| 1 2 3 4 5 6 7 8 9 10 20 30 40 50 60 70 80 90 100 110 120 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0 11.0 12.0 |
9.9667229(-02) 1.9735435(-01) 2.9115966(-01) 3.7933365(-01) 4.6034390(-01) 5.3292733(-01) 5.9612751(-01) 6.4931524(-01) 6.9219214(-01) 7.2477829(-01) 6.3998836(-01) 3.9316690(-01) 2.7039629(-01) 2.0924576(-01) 1.7175008(-01) 1.4597256(-01) 1.2705277(-01) 1.1253712(-01) 1.0103162(-01) 9.1679864(-02) 8.3924539(-02) |
9.96673339(-02) 1.97354548(-01) 2.91159949(-01) 3.79334008(-01) 4.60344283(-01) 5.32927735(-01) 5.96127869(-01) 6.49315541(-01) 6.92192369(-01) 7.24778459(-01) 6.39988075(-01) 3.93166879(-01) 2.70396296(-01) 2.09245757(-01) 1.71750051(-01) 1.45972614(-01) . . . . . |
| Table 6. Solutions affected with error's | ||||
|---|---|---|---|---|
| t | y' +ty=0 | y" +ty' +y=0 | True | exp |
| 0.1 0.2 0.3 4.8 5.3 5.7 5.8 9.6 13.2 13.3 |
9.9501247 9.8019867 9.5599747 9.9309967 7.9517440 8.8123642 4.9590409 9.8055567 1.4567406 3.8621109 |
9.9501247 9.8019867 9.5599756 9.9511737 8.1370781 1.05(-6) 6.64(-7) 9.98(-8) 7.22(-8) 7.16(-8) |
9.95012479 9.80198673 9.55997478 9.92949522 7.94938558 8.80816483 4.95639984 9.72094942 1.45970747 0.00000000 |
0 0 0 -05 -06 -07 -07 -20 -37 -38 |
. . もう一つ、区間幅の誤差に起因する原因がある。区間幅hが有効桁5桁の少数、例えば、0.014159なら、10進5桁の計算ではt0=12.300に対してt0+h=12.314となる。従って、有効な区間幅hは0.014000であり、t0の値によっては小数第3位に誤差を生ずる。従来の積分法はh×fの計算にh=0.014159を使用するから、(1.24)のような微分方程式の場合には解は多くの精度を失う。通常は区間幅として0.1, 0.01, …のような値を使用するけれども、これらは2進法では循環小数であり、上に述べたことと同じ結果になる。
. . Table 8は上記のtについての誤差のない場合の(1.24)及び(1.27)の解の値を示す。これは、tの少数第3位が最小の誤差を持つなら解は3桁正確であることを示す。数値解法の場合にはもっと悪い結果になる。その理由は、2分の1区間幅の小数部が異なることにより区間幅が等間隔でないからである。
| Table 8. Valid h and True solutions. | |||
|---|---|---|---|
| t=12.31400… | t=12.31415926535… | t=12.31500… | |
| 4.48846403…×10−6 | 4.48774923…×10−6 | 4.48397781…×10−6 | |
| 1.18294852…×10−33 | 1.18063078…×10−33 | 1.16847043…×10−33 | |
. . これらの理由により、(1.2)の手順[3]では区間2hの代わりにh2=x2−x0が使われ、Program 1 では精度の比較のための真の解を計算するためにX#=Xという代入が行われる。