3�D ������������̐��l��@�̏����
3.1�@��`�@�̕s����
. .
Milne �@�� Runge K. �@�ɔ�ׂĐ��x�������A(1.1)�̐��l���� x=0 ���� h=0.05 �ŋ��߂Ă����� x=5 �ȏ�ł͗L�����͂Ȃ��Ȃ�A�����Ɍ������U�����Ȃ���U�������債�Ă����B����͌덷�̓`�d�ł͓�������ł��Ȃ��̂Ő��l�I�s���茻�ۂƌĂꗝ�_�I�ɂ��ؖ��ł����ƌ��Ȃ���Ă���l�ł��邪�A���҂͐��l�I�s����ƒ�`���ׂ����ۂł͂Ȃ��A������������̐��l��@����̌Œ莟���ߎ��ŁA���A�Œ�敪���ł��邱�ƂɋN�������@�̓K�p���E���z���Ă���̂ł���A���̗l�ȉ�@�Ő���������������ƍl���邱�Ƃ��{���I�ɊԈ���Ă���ƍl����B
. .
Cp+1[a, b]�Ȃ�C�ӂ̊��� Newton �̑O�i��Ԍ����� Tayler �W�J�ŋߎ�����ꍇ�A���̑S��`��ɓn���ē���敪���A���ꎟ���ŁA���A���ꐸ�x�ŋߎ����邱�Ƃ͈�ʓI�ɂ͏o���Ȃ��B���l�ϕ��ɂ����Ă͔�ϕ����ɂ�萸�x���قȂ邾���łȂ��A������ł��ꏊ�ɂ�蒘�������x���قȂ�A�P�X�e�b�v�̐ϕ��ŗL�����̖����Ȃ�ꍇ���炠�邱�Ƃ͑O�߂Ɏ������B������������̐��l��@�����l�ϕ��ł��邩�瓯�l�̌덷���A�P�Ȃ鐔�l�ϕ��Ƃ͈قȂ�A���̌덷�͎��̃X�e�b�v�ɏo���l�̌덷�Ƃ��ĉe����^����B��̌Œ莟���A�Œ�敪���̉�@�ł͂��̌덷�̗ݐς�}�����Ȃ����Ƃ��K�p���E���z���錴���ƂȂ�A���l�I�s���茻�ۂƌĂ�錻�ۂ���̂ł���B
. .
����������� dy/dx=f(x, y)��C�ӂ̓_ x0����x1=x0+h �� Euler �@�ŗ\�����A��`�@�ŏC�����ĉ����ƁA���m�� f1 �Ɏ����ł����Ƃ����Ό덷��(2.17)�ŗ^������B
 ___________(3.1)
___________(3.1)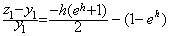 ___________(3.2)
___________(3.2). . �P�X�e�b�v�̑��Ό덷�� ε �ƒu���Ax0 ���� xn=x0+nh ���A�����ɉ� yk �̋ߎ��l zk ���v�Z�����Ƃ��̗ݐό덷�͎��̂悤�ɂȂ�B
x0 �ɂ����� y0=a �̉��́A__________
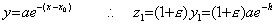
(x1, z1)�������l�Ƃ�����́A________
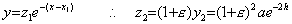
(x2, z2)�������l�Ƃ�����́A________
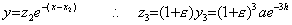
�ȉ����l�ɂ��āA(xn−1, zn−1)�������l�Ƃ�����́A
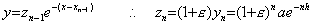
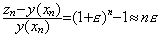 ___________(3.3)
___________(3.3). . ���̉��̐��x�����P����ɂ� h ��������������Ȃ����An �� h �ɋt��Ⴕ�đ�������̂� ε ������ȏ�ɉ��P����Ȃ���Ό��ʂ��Ȃ��B���̏ꍇ�́Ah=0.05 �ɂ����(3.2)���ε=−1.0681×10−5 �ƂȂ�̂łP�����x�̐��x���P���]�߁A����� h ������������ΑS��ŒP���x�̉��邱�Ƃ��ł���B�������A���_�v�Z�ƈقȂ�Ah ����������������� x+h �̌v�Z�� h ��������邱�Ƃ� n �̑����ɂ��Ax �̑傫���Ƃ���ł̐��x�͗��_�l���͉��P����Ȃ��B
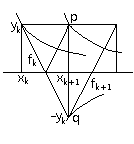 �} 3.1 |
. . �̂ɁA(3.2)�A(3.3)�̎g�p��������E�� x �ɊW�Ȃ����̂悤�ɂȂ�B
. . �������������A___________
 ___________(3.4)
___________(3.4)�̏ꍇ�ɂ́A�C�ӂ� x0 ����P�X�e�b�v�̉��̑��Ό덷��(2.20)���A
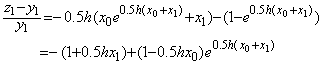 ___________(3.5)
___________(3.5)x0 �ɂ����� y0=a �̉��́A______
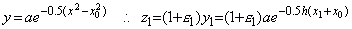
(x1, z1)�������l�Ƃ�����́A____
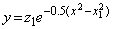
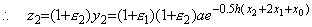 ____
____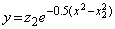
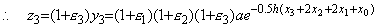
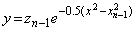
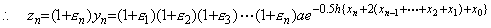
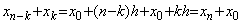 ____�ɂ��{ }�̒�������ƁA
____�ɂ��{ }�̒�������ƁA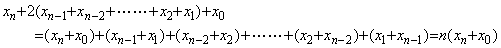
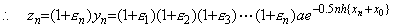
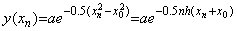 �ł��邩��ݐό덷�̑��Βl�́A
�ł��邩��ݐό덷�̑��Βl�́A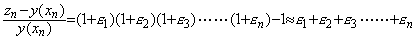 ___(3.6)
___(3.6). . ���̏ꍇ�ɂ́Ah<1 �ł� Euler �@�ɂ��\���l���떔�͕��ɂȂ邱�Ƃ��N����B
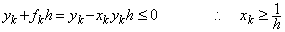

| �\ 3.1 x0=0 ��� xn ���̗ݐϑ��Ό덷�ƕs���� | |||||
|---|---|---|---|---|---|
| xn | �ݐϑ��Ό덷�̗��_�l | h=0.5 �̐��l�� | �^ �l | ||
| h=0.1 | h=0.5 | �C����20�� | �C����21�� | ||
| h 1.0 2.0 3.0 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0 9.0 10.0 |
1.25208×10−5 1.07736×10−3 1.74273×10−3 −6.56812×10−3 −3.90923×10−2 −7.06485×10−2 −1.15783×10−1 −1.76409×10−1 −2.53271×10−1 −3.45328×10−1 −4.49270×10−1 −5.59424×10−1 −6.68277×10−1 −8.50824×10−1 −9.55597×10−1 |
8.14845×10−3 3.14543×10−2 5.77183×10−2 −2.96036×10−1 −1.05177×10 0 −9.41751×10−1 −1.15108×10 0 −2.70822×10−1 −6.94063×10 0 7.62576×10 1 −1.54732×10 3 4.64174×10 4 −2.04983×10 6 −1.20181×1010 −2.85004×1014 |
8.88889×10 0 6.22222×10 0 1.41414×10 0 9.25918×10−2 −6.21529×10−3 −6.55409×10−2 −6.79378×10 0 5.52986×103 −2.94219×10 7 8.77619×1011 −1.28826×1017 8.31974×1022 −2.14462×1029 : |
8.888899×10 0 6.222229×10 0 1.414149×10 0 9.372549×10−2 1.408009×10−2 1.670349×10−1 2.162209×10 1 2.419389×10 4 1.930789×10 8 9.358699×1012 2.404099×1018 2.911109×1024 1.500829×1031 : |
8.82496×10 0 6.06530×10 0 1.35335×10 0 1.11089×10−1 3.35462×10−3 4.00652×10−4 3.72665×10−5 2.69957×10−6 1.52299×10−7 6.69158×10−9 2.28973×10−10 6.10193×10−12 1.26641×10−13 2.57675×10−17 1.92874×10−21 |
. . �]���A����͐��l�I�s���茻�ۂƌĂ�Ă��邪�A��L�ɏq�ׂ��悤�ɁAEuler �@�ŗ\������`�@�ŏC�������@��K�p���E���z���ċ��s�������ʂł���A�\ 3.1 �̐Ԏ��\���ȍ~�̐��l�͉��Ƃ��ĉ��̈Ӗ��������Ă��Ȃ����A���e���Ƃ����l�I�s���茻�ۂƌĂԂׂ����̂ł��Ȃ��B���̓K�p���E�̐��m�Ȓl�͐} 3.1 �Ɏ����悤�ɂQ��ڂ̏C���_�� q �_�A�����A�\���l�Ɉ�v����Ƃ��� x �̒l�ł��邪�Ah �����łȂ������������̌`�Ɉˑ�����B
. . ���̂悤�ȗ̈�ɉ����Ă��V���ɏ����l��ݒ肵�Ah �����������Čv�Z����ΐ������������߂邱�Ƃ��o���邪�A����� h �ɔ���Ⴕ�ĉ�@�̎g�p�\�͈͂��L���邩��ł���B���A�悭�m���Ă���悤�ɁAx �̑傫���������Ɍ������ĉ������߂��ꍇ�ɂ͕s���茻�ۂ������Ȃ����A��������(3.4)�̏ꍇ�ɂ͂��͈̔͂ł� Euler �@�ɂ��\���l�����ɂȂ邱�Ƃ��N���Ȃ����A�P�X�e�b�v�̑��Ό덷(3.5)�����ł���̂ŋߎ��������ɂȂ邱�Ƃ��N���Ȃ�����ł���B
3.2�@Runge K. �@�̕s����
. .
���������� dy/dx=f(x, y)�� Runge K. �@�ʼn����Ƃ��A�敪�� h �̂Q��Ԃ��P�X�e�b�v�ʼn����ƌ�����(3.7)�ŕ\�����B�A���͒��ԓ_ x1=x0+h �̊��l y1 �� Euler �@�ŗ\�����A���̓_�� f �����߂邱�Ƃ��Ӗ����A�B���͌�� Euler �@ y0=y1−f1h �ɂ��C�����čēx���� f �����߂邱�Ƃ��Ӗ�����B�C���͏C�����ꂽ f �ɂ�� x2=x0+2h �̊��l�𒆓_�@�ŗ\������ f �����߁A�D���͒��ԓ_ x1 �̗\���l�y�яC���l�ɑ��� f�A�����A�A�B�̕��ϒl�����̓_�� f �Ƃ��� Simpson �̌����ɂ��ϕ����邱�Ƃ��Ӗ�����B�]���āA�����R�_�� f �̐��m�l�����܂����Ƃ��A���̐��x�� Simpson �̐ϕ������̐��x�ɓ������Ȃ�A�D���� y2 �� z2 �ƒu���� Runge K. �@�̂P�X�e�b�v�̑��Ό덷��(2.21)�ŗ^������B
. .
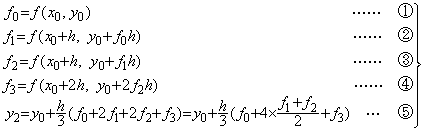 ___________(3.7)
___________(3.7). . ����������(3.1)�̏ꍇ�ɂ́A�C�ӂ� x0 �ɂ�����P�X�e�b�v�Q��Ԃ̐��l���̑��Ό덷�͐��m�� f0, (f1+f2)/2, f3 �����܂����Ƃ���(3.1)�̉���(2.21)�ɑ�������(2.22)�Ɠ����ɂȂ�B�]���āA�S��ɓn���đ��Ό덷�͓����ŁAh �݂̂ɂ���܂�Ah=0.1 �ł͗L�����V��(−1.22855×10−7)�Ah=0.05 �ł͗L�����X��(−3.65068×10−9)�ł���B�]���̔�r�̎d���ł� Runge K. �@�� Milne �@�ɔ�חL�����łQ���L���ƂȂ�B
. . n �������Ƃ��Ax0 ���� x0+nh �������ɉ������߂��ꍇ�̗ݐϑ��Ό덷�͑�`�@�̏ꍇ�Ɠ��l�ɂ��ċ��߂邱�Ƃ��o���A�P�X�e�b�v�łQ��Ԑi�s���邩��(3.3)�̓��o�ߒ��ŃX�e�b�v���� n/2�A�敪���� 2h �ɒu��������悢�B�̂ɁA
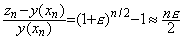 ___________(3.8)
___________(3.8). . ���ۂɂ́ARunge K. �@�� x1, x2 �ɂ����� f �̒l�͐��m�ɂ͋��܂�Ȃ��̂łP�X�e�b�v�̑��Ό덷��(3.7)���狁�߂Ȃ���Ȃ�Ȃ��B
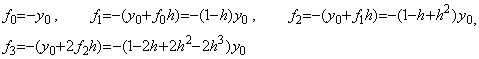
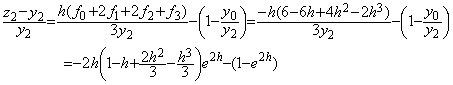 ___________(3.9)
___________(3.9). . ���̔����������̏ꍇ�A(3.7)�ɂ����Ē��_ x0+h �̗\���l�ƏC���l�y�� x0+2h �̗\���l�̂ǂꂩ���떔�͕��ƂȂ����Ƃ�����Ȍ��ʂ͓����Ȃ��Ȃ�Bx0+h �ɂ�����\���l�� y0+f0h=(1−h)y0 �ł��邩�� h<1 �ł͐��A�C���l�� y0+f1h=(1−h+h2)y0>0 �ł���A�Ō�̗\���l y0+2f2h=(1−2h+2h2−2h3)y0 �� h<0.6…�ł͐��ł���B���A�ݐϑ��Ό덷�����ł��邩��ߎ����͏�ɐ��ł���B�]���āA�P�X�e�b�v�̋敪���� 2h<1 �ł�������錶�e���͐����Ȃ��B
. . ����������(3.4)�̏ꍇ�ɂ́A�C�ӂ� x0�ɂ�����P�X�e�b�v�̐��l���̑��Ό덷�͐��m�� f0, (f1+f2)/2, f3 �����܂����Ƃ���(3.4)�̉���(2.21)�ɑ������ASimpson �� 1/3 ���̑��Ό덷(2.23)�Ɠ����ɂȂ�B�]���āA���x�� x0 �ɂ��قȂ�Ah=0.1 �̂Ƃ� x0=0 �ɂ����Ă͗L�����V���ł��邪(−1.67501×10−7)�Ax0=10 �ɂ����Ă͐^�l����o�����ĂP�X�e�b�v�ŗL�����Q��(−3.03927×10−2)�����Ȃ��B����͌덷�̓`�d�ł͂Ȃ��Bh=0.05 �ł͂��ꂼ��L�����X��(−2.60742×10−9)�ƂS��(−5.37379×10−4)�ƂȂ�A�]���̔�r�̎d���ł� Runge K. �@�� Milne �@ �ɔ�ׂėL�����łQ���L���ƂȂ�B
. . n �������Ƃ��Ax0 ���� x0+nh �������ɉ������߂��ꍇ�̗ݐϑ��Ό덷�͑�`�@�̏ꍇ�Ɠ��l�ɂ��ċ��߂邱�Ƃ��o����P�X�e�b�v�łQ��Ԑi�s���邩��(3.6)�̓��o�ߒ��ŃX�e�b�v���� n/2�A�敪���� 2h �ɒu�������Aεk �� k �������Ƃ�(2.23)�̓Y���� 2 �� k �ɁA1 �� k−1 �ɁA0 �� k−2 �ɒu��������悢�B�̂ɁA
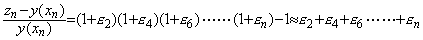 ___________(3.10)
___________(3.10). . ���̏ꍇ�����ۂ� Runge K. �@�� x1, x2 �ɂ����� f �̒l�͐��m�ɂ͋��܂�Ȃ��̂łP�X�e�b�v�̑��Ό덷��(3.7)��p����(3.9)�Ɠ��l�ɋ��߂Ȃ���Ȃ�Ȃ��B
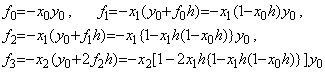
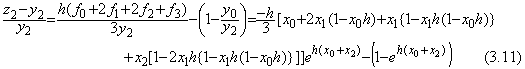
| �\ 3.2 dy/dx=−xy ,___y0=10 (�X�e�b�v��=2h) | |||||
|---|---|---|---|---|---|
| xn | h=0.1 | h=0.25 (*�̐^�l=8.82496) | �^ �l | ||
| ���_���Ό덷 | �� �l �� | ���_���Ό덷 | �� �l �� | ||
| 2h 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0 |
−6.77422E−9 1.15426E−6 1.75014E−4 2.43666E−3 1.61592E−2 7.35364E−2 2.76247E−1 1.01209E00 4.65713E00 4.29526E01 1.57251E03 |
9.80199____ 6.06531____ 1.35359____ 1.11361E−01 3.40883E−03 4.00069E−05 1.94372E−07 4.60717E−10 7.16428E−13 1.13255E−15 3.03491E−18 |
−1.12447E−5 −5.98691E−5 8.54474E−3 1.77018E−1 2.11227E00 5.59433E01 1.23652E04 3.11624E07 7.77049E11 1.64140E17 2.58049E23 |
8.82487 * 6.06494 1.36492 1.30755E−01 1.04405E−02 2.12208E−03 1.88338E−03 7.13537E−03 9.84067E−02 4.22950E00 4.97713E02 |
9.801986 6.065306 1.353352 1.110899E−01 3.354626E−03 3.726653E−05 1.522998E−07 2.289734E−10 1.266416E−13 2.576757E−17 1.928749E−21 |
. . ���̔����������̏ꍇ�� Runge K. �@�̓K�p���E�͒��ԓ_�̗\���l���떔�͕��ɂȂ����Ƃ��ŁAyk+f0h=(1−xkh)yk>0 �ɂ�� xk<1/h �ƂȂ�Bh=0.25 �ł� x<4 �ŗǂ������Ă��邪�Ah=0.1 �ł� x<10 �ƂȂ���E���L������B���ۂɂ͂�����O�� xk+2h �̓_�̗\���l���떔�͕��ƂȂ�(3.7)�� f03�����ɂȂ�̂ŁA���̐��x�͗L�����P���ɂ��������g�p�ɑς�����̂ł͂Ȃ��B���̌��E�́A
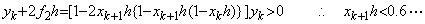
3.3�@Milne �@�̕s����
. .
Milne �@�̂P�X�e�b�v�̗\���q�y�яC���q��(3.12)�ŗ^������B�\���q�@�� x0, x1 �y�т�����O�̂Q�_ x−2, x−1 �ɂ�������l�����m�ł��邱�Ƃ�O��Ƃ��A��ϕ��� f �������̓_�Ŋ��m�ł���S�_��ʂ�R�����ŋߎ����A���[x−2, x2]��ϕ����邱�Ƃɂ�� y2�����߂���̂ł���B�������A�C���q�A�͗\���_���܂ނR�_��p����[x0, x2]�� Simpson �� 1/3 ���ɂ��ϕ�������̂ł���A�C���̌J�Ԃ��ɂ�萳���� f2 �Ɏ��������Ƃ� y2 �̐��x��Simpson �� 1/3 ���̐��x�Ɉ�v����B
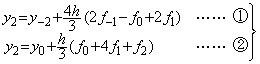 ___________(3.12)
___________(3.12). . Milne �@�͏C���q�łQ��Ԑϕ����ĂP��Ԃ����o���_���i�s���Ȃ��̂ŃX�e�b�v�����Q�{�ɂȂ�̂���̌����ŁA����ɂ��ݐϑ��Ό덷�͂Q�{�ɂȂ邪�A�����Əd��Ȍ����͏C���q�̐ϕ���Ԃ̒��ԓ_�̒l��O�̃X�e�b�v�ŋ��߂��ߎ��l�ɌŒ肷�邱�Ƃɂ���A����ɂ�蒘�����덷����B����������(3.4)�̏ꍇ�ARunge K. �@�͂P�X�e�b�v�̌v�Z�� ε>0 �̌덷�������Ă����̃X�e�b�v�̏������z�� f=−x(y+ε)�ƂȂ�AEuler �@�̌v�Z�l������������A�����A���̒l�����������A�덷�̕���ʂ�����B����AMilne �@�͌덷�������p�����̂Ō덷�̑傫�����ł͋}���ɐ��x����������B
. . �������l y−2, y−1, y0, y1 ��^���� y2 ��\�����Ay0, y1, y2 ��p���� y2 �̏C�������������Ƃ���B���̎����l�Ɛ^�l y �Ƃ̌덷��ε>0�Ƃ���ƁAy2=y+ε �ł���B���̃X�e�b�v�� h �����i�s���邩�炱�̏C���l�� y1 �ɂȂ�A���̓_ x1 �ɂ�������z f1 �Ɛ^�l y �ɑ�����z f �̊W�y��(3.12)�@�̗\���l�͎��̂悤�ɂȂ�Byf �� x1 �ɂ�������z�ɐ^�l f ��p�����\���l�A�����A�ŏ��̃X�e�b�v�Ɠ��l�ɐ^�̏o���l�S�_��^�����ꍇ�̗\���l�ł���B���̌��ʁAy2 �̗\���l�� f1 �̌덷�Ɉˑ�����덷�����Z�����B
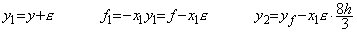
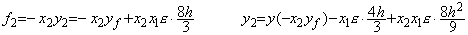
3.4�@���̑��݂ƈ�Ӑ�
. .
����������(3.13)�͏]���̐��l��@�ł͉������Ƃ��ł��Ȃ��Ƃ���Ă���B���̗��R�͊� √y, (y≥0)�� y=0 �� Lipschitz ���������Ă��Ȃ��̂ʼn�����ӂłȂ�����ł���Ƃ�����B�m���ɂ��̉���(3.14)�Ɏ����悤�ɖ����ɑ��݂��邪�A���ϖ@�ł͉������Ƃ��ł���̂ł��邩��A������ӂłȂ����Ƃ͐��l��@�ʼn����Ȃ����R�ɂȂ�Ȃ��B���ہA��`�@�⒘�҂̉�@�ł͐��m�ɉ������Ƃ��ł���B
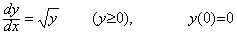 ___________(3.13)
___________(3.13)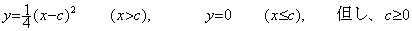 ___________(3.14)
___________(3.14). . ���l��@�ɂ����ẮAEuler �@�ł͂Q���ARunge K. �@�� Milne �@�ł͂R���̓����܂ŘA���łȂ��Ə�]�����Ӗ��������Ȃ�����(3.14)�̉��ڋ��߂邱�Ƃ͂ł��Ȃ��B�������Ay=x2/4 �܂��� y=0 �͋��܂�Ȃ���Ȃ�Ȃ����A�����̉�@�ł͌�҂͋��܂邪�O�҂͋��܂�Ȃ��Bx=0 �� Lipschitz ���������Ȃ����A�Œ�_�ł��邩�獷���x���Ȃ��̂ł���A�O�҂����܂�Ȃ��̂͒P�ɏ����l����я������z�����ɗ�ł��邱�Ƃɂ��BEuler �@�� Runge K. �@�ł͏������z f0=0 �̏ꍇ�ɂ� x1=x0+h �̊��l�� y1=y0 �ł���Ay0=0 �ł��邩�� y1=0�A���̓_�̌��z��(3.13)�ɂ�� y �݂̂Ō��܂邩�� f1=0 �ƂȂ�B�]���āA�S�Ă̓_�� y=0 �ƂȂ�BMilne �@�ł͏o���l�������̕��@�ŋ��߂邩���͂蓯���ł��邪�A�ʂ̕��@�ɂ�菉���l�ȊO����łȂ��������o���l��^����� y=x2/4 �𐳊m�ɋ��߂邱�Ƃ��ł���B
. .
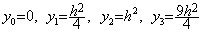 _____��^����A_____
_____��^����A_____
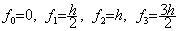
�\���l�́A_______
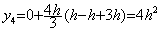 _______����āA_______
_______����āA_______
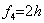
�C�����āA_______
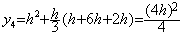 _______����āA�����B
_______����āA�����B. . ���ϖ@�ɂ����Ắ@y=0�@�ł͂Ȃ��Ƃ��������p���ĉ�����ӂɐ������Ă���̂ł��邩�琔�l��@�ł��P���I�ɂ͗�łȂ��Ƃ��������p����悢�B��L�́@Milne�@�@�̏o���l�͂�����Ӗ����Ă���B�����l�݂̂���o���ł����@�ł́@y1=ε, (>0)�Ƃ���Ηǂ��̂ł��邪�A�����C���̂ł��Ȃ� Euler �@�� Runge K. �@�ł͐��������ʂ邱�Ƃ͂ł��Ȃ��B�]���āA������p���� Milne �@���� P-C �@�ł͐������������Ƃ��ł��Ȃ��B����������ł��ȒP�ȕ��@�͑�`�@�ɂ�蔽���C�����邱�Ƃł���A�����͒x�����敪�� h �ɊW�Ȃ����������Ɏ�������B
. . y0=0, y1=ε �ł��邩��(3.13)�ɂ��Af0=0, f1=ε1/2 �ł���B�̂ɁA
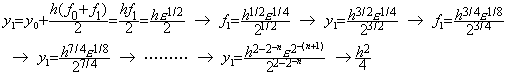
. . ��`�@�� y≡0�ł͂Ȃ��������߂邽�߂ɂ� Euler �@�ɂ��\���l�ɑ�(3.15)�̏������v���O��������悢�B���l���̎����\ 3.3 �Ɏ����B�\�̐^�l�� x �ɑ��闝�_�l�Ƌ͂��ɂ���Ă���̂� x �̌v�Z�@�����̂Q�i�l���P���x�̊ۂ߂ɂ��^�� x �ɑ��͂��ɂ���Ă��邪�A�O���\�i�ϊ��̊ۂ߂ɂ�� x �̊O���\���ɂ��ꂪ����Ȃ�����Ő^�l�̌��ł͂Ȃ��B
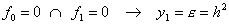 ___________(3.15)
___________(3.15)| �\ 3.3____dy/dx=√y ,____y(0)=0____(h=0.2) | |||||
|---|---|---|---|---|---|
| x | �� �l �� | �^�@�@�l | x | �� �l �� | �^�@�@�l |
| 0.2 0.4 0.6 0.8 1.0 |
1.000001E−2 4.000003E−2 9.000005E−2 1.600000E−1 2.500000E−1 | 1.0000000E−2 4.0000001E−2 9.0000007E−2 1.6000000E−1 2.5000000E−1 |
1.2 1.4 1.6 1.8 2.0 | 3.600001E−1 4.900001E−1 6.400001E−1 8.100001E−1 1.000000E00 | 3.6000002E−1 4.8999998E−1 6.4000001E−1 8.1000006E−1 1.0000000E00 |
. . dy/dx=x, y(0)=0 �̉��� y=x2/2 �ł��邪�A�ʏ�́Af0=0 �ł��邩�� x1=h �ł� y1=f0h=0 �ƂȂ��Ă��܂��Bf �� y ���܂܂Ȃ����炱��ȍ~�� f �͐������l�ƂȂ邪�A���͐^�̉��s�ړ����� y=x(x−h)/2 �ƂȂ�B�����Ady/dx=x−h/2, y(0)=0 �̉��ɉ����Ă��܂��B���̉��͕\ 3.4 �Ɏ����悤�ɁAh ��@���ɏ��������Ă����̔����������̐��l���Ƃ͌����Ȃ����̊u��������B����͌������A����A�ۂߌ덷�₻���̓`�d�ł͂Ȃ��A�������z����ł���ꍇ�ɂ� Euler �@��[x0, x0+h]�̐ϕ��̑��Ό덷�� −1 �ł��邱�ƂɌ���������B�����y�ѕ\ 3.4 �Ɏ����悤�� x �̑傫�����ł� h �̉e�����������A���l���̐��x�͂悭�Ȃ�B���̏ꍇ���Ay1=ε>0 �����肷��� f1=x1=h�A��� Euler �@ε−f1h=0 �ɂ�� ε=h2 �ƂȂ�A��`�@�ɂ��C���Ő��������Ɏ�������B���ہAf1 �� f0=0 �Ƃ̕��ϒl���g���� 2ε−f1h=0 �ɂ��ȒP�ɐ���������������B
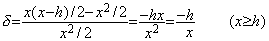
| �\ 3.4____dy/dx=x ,____y(0)=0____(Euler) | ||||
|---|---|---|---|---|
| x | �� �l �� | y=x(x−h)/2 | δ | y=x2/2 |
| 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 |
0 1.000000E−2 3.000000E−2 6.000000E−2 1.000000E−1 1.500000E−1 2.100000E−1 2.800000E−1 3.600000E−1 4.500000E−1 |
0 1.000000E−2 3.000002E−2 6.000001E−2 9.999999E−2 1.500001E−1 2.099999E−1 2.800000E−1 3.600003E−1 4.499999E−1 |
−1.0 −0.5 −0.333333 −0.25 −0.2 −0.166667 −0.142857 −0.125 −0.111111 −0.1 |
5.0000001E−3 2.0000000E−2 4.5000003E−2 8.0000002E−2 1.2500000E−1 1.8000001E−1 2.4499999E−1 3.2000001E−1 4.0500003E−1 5.0000000E−1 |
. . x=0 ������� x0=h, x1=2h �Ƃ����
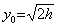
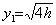 �ł��邩��A������ f0, f1 ��p������`�@�̐ϕ��l���ߎ����Ƃ��āA�P�X�e�b�u�̉��̑��Ό덷��(2.17)�ɂ��v�Z����Ǝ�����ε1 �ƂȂ�̂ŁAh �ɊW�Ȃ��L�����Q���̐��x���������Ȃ��B
�ł��邩��A������ f0, f1 ��p������`�@�̐ϕ��l���ߎ����Ƃ��āA�P�X�e�b�u�̉��̑��Ό덷��(2.17)�ɂ��v�Z����Ǝ�����ε1 �ƂȂ�̂ŁAh �ɊW�Ȃ��L�����Q���̐��x���������Ȃ��B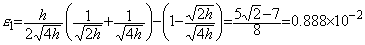 _______(3.16)
_______(3.16)| �\ 3.5 dy/dx=1/y, h=0.1, x0=h | �\ 3.6 h=0.1, x0=h×10−6 | ||||||
|---|---|---|---|---|---|---|---|
| x | A | B | �^�@�l | x | �������� | �^�@�l | |
| 0.1 | 0.447213 | 0.450000 | (�����l) | 10−7 | 4.47213×10−4 | (�����l1) | |
| 0.2 0.3 0.4 0.5 : 1.0 2.0 3.0 4.0 5.0 : : 10.0 : : 100.0 |
0.637454 0.779994 0.899673 1.00500 : 1.41819 2.00297 2.45196 2.83058 3.16421 : : 4.47352 : : 14.1426 |
0.639319 0.781506 0.900981 1.00617 : 1.41902 2.00355 2.45243 2.83100 3.16459 : : 4.47378 : : 14.1427 |
0.6324555 0.7745966 0.8944271 1.0000000 : 1.4142135 2.0000000 2.4494897 2.8284271 3.1622776 : : 4.4721361 : : 14.142135 | 0.1 0.2 0.3 0.4 0.5 : 1.0 2.0 3.0 4.0 : : 10.0 : : 100.0 |
111.804 111.805 111.806 111.807 111.808 : 111.812 111.821 111.830 111.839 : : 111.893 : : 112.694 |
(�����l2) 111.8052 111.8060 111.8069 111.8078 : 111.8123 111.8212 111.8302 111.8391 : : 111.8928 : : 112.6942 | |
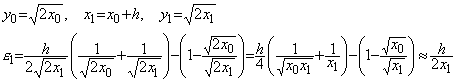
. . h ��菬�����_�� x0 �ɑI�ԂƂP�X�e�b�v�̑��Ό덷���������傫���Ȃ�̂ł��̔����������𐳂����������Ƃ͏o���Ȃ��Bx0=ah, (a<1)�Ƃ���A
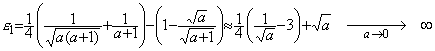
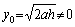 �ł��邩��x≥x0, y≥y0 �ł� Lipschitz ���������Ă��邪�Aa=10−6 �ɂƂ�ƂP�X�e�b�v�̑��Ό덷�͖� 250 �ƂȂ萳�������͓����Ȃ��Bh=0.1 �ʼn��������l����\ 3.6 �Ɏ����B�ŏ��̂P�X�e�b�v�� 0.447 �ƂȂ�ׂ����̂� 112 �ɂ��Ȃ�A���̌�͖w�Ǖω����Ȃ��B���ۂɂ́A���ꂩ���� x0=0.1, y0=111.804 �̉������߂邱�Ƃɕς���Ă��܂����̂ł���B���̉��́A
�ł��邩��x≥x0, y≥y0 �ł� Lipschitz ���������Ă��邪�Aa=10−6 �ɂƂ�ƂP�X�e�b�v�̑��Ό덷�͖� 250 �ƂȂ萳�������͓����Ȃ��Bh=0.1 �ʼn��������l����\ 3.6 �Ɏ����B�ŏ��̂P�X�e�b�v�� 0.447 �ƂȂ�ׂ����̂� 112 �ɂ��Ȃ�A���̌�͖w�Ǖω����Ȃ��B���ۂɂ́A���ꂩ���� x0=0.1, y0=111.804 �̉������߂邱�Ƃɕς���Ă��܂����̂ł���B���̉��́A
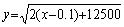 �ł���A�\ 3.6 �̐��l���͂��̐^�l�ɗǂ���v���Ă���B
�ł���A�\ 3.6 �̐��l���͂��̐^�l�ɗǂ���v���Ă���B. . �ŏ��̃X�e�b�v�̑��Ό덷����������ƂȂ闝�R�͑�`�@�̕��ό��z(f0+f1)/2 �����ϒl�̒藝�ɂ����z�ƒ������قȂ邩��ł���Aa→0 �ł� f→∞ �ł��邩���`�@�̕��ό��z��������ƂȂ�̂ŁAx0=0, y0=0 ����� f0 ��p�����������Ȃ��B�]���āA���̂Ƃ����������Ȃ����R�� Lipschitz �����Ƃ͊W�Ȃ��A�P�X�e�b�v�̑��Ό덷��������ɂȂ��Ă��܂�����ł���B���[0, h]�ł����ϒl�̒藝�������z�͑��݂��A���ꂪ���܂�� x1=h �ɂ�������͋��܂�B���̔����������̉��� x �̏������Ƃ���ł̕��ϒl�̒藝�������z�͋敪�_�̌��z�̕��ςł͂Ȃ��Ay ��Ɨ��ϐ��ɂ���� dx/dy=y �ƂȂ���� x=y2/2 �ł��邱�Ƃ��疾�炩�Ȃ悤�ɁA�敪�_�̌��z�̋t���̕��ς̋t���ł���B���҂̍����������傫���̂ő�`�@�̐��x�͒����������̂ł���Bx0=0 �ł� f0→∞ �ł��邩���҂̕��ς� 2f1 �ƂȂ�Ay1=2f1h �� f1 ����������ΐ��������ł���B�������A������ f1 �邽�߂� y1 �ɓK���Ȓl��^���Ĕ����C������ƂQ����ƂȂ�������Ȃ��B���̏ꍇ�� y1 �����肵�Č�� Euler �@�� y0 �����߁A���ꂪ��ɂȂ�悤�� y1 ���C�����Ă���̂�����Ax0=0 �� Lipschitz ���������Ȃ���Ȃ�Ȃ��B
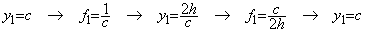
. . ��ʂɁAdy/dx=1/yn, y0=0, (n>0)�̂Ƃ������l�ɂ��ĊT���� y1 �����߂邱�Ƃ��ł��邪�A���m�Ȓl�����߂�ɂ͕��ό��z�́Af0 �̋t���� n �{�� f1 �̋t���Ƃ̘a�|���� 1/(n+1)�̋t���A�����A(n+1)f1 �Ƃ��Ȃ���Ȃ�Ȃ��B���̕��ό��z�������Ɏ����悤�� f1 ����������Ε��ϒl�̒藝�̌��z�Ɛ��m�Ɉ�v����B
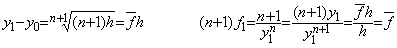
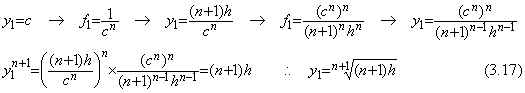
. . ���̉�@�͔����������̋��ω����������Ă��邩�畽�ϒl�̒藝�̌��z�����������̂ł���Ax=0 ����̐��l��@�Ƃ��ēK���ł͂Ȃ��B�����ŁAx0=0 �ɂ����� f0 ���g�p���Ȃ����߂Ɍ�� Euler �@�̔����C���ɂ�� y1 �̊T���l�����߂�ƁA(3.18)�̕����_�����߂邱�ƂɂȂ邪�A�����Ɏ����悤�ɂ�����k���ʑ��ɂȂ�Ȃ��̂ŕ����_�����߂邱�Ƃ͏o���Ȃ��B
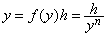 _______(3.18)
_______(3.18)

. . y' =1/y, y(0)=0 ���Q�͂̃v���O����1(�o�͂� 80 �s�� 28 �s�̕K�v�Ȃ��̂����ɕύX)�ʼn��������ʂ�\ 3.7 �Ɏ����Bx=0�`1 �� 10 ���������_�̉������߂邽�߁A��� 0.1 ���W���������ŏ��̓_ x0=0.0125 �ɂ����� y0=0.158114 ���Q�� 2.2 �߂ɏ]���ē��͂���BE �͕\�̂P��� h ���X�� E �������� E ���ߎ��Ŏ������邱�Ƃ������B��̌Œ莟���A�Œ�敪����@�ł͂��ꂾ���̐��x�͒B���ł��Ȃ��B
| �\ 3.7 y' =1/y, y(0)=0 (x0=0.0125, y0=0.158114, h=0.0125�`0.05) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IB | E | x | y | �^�@�@�l | IB | E | x | y | �^�@�@�l | |
| 1 2 3 |
7 6 5 5 4 4 4 4 4 4 4 4 4 4 4 4 4 3 3 4 4 |
0.025 0.0375 0.05 0.0625 0.075 0.0875 0.1 0.1125 0.125 0.1375 0.15 0.1625 0.175 0.1875 0.2 0.2125 0.225 0.2375 0.25 0.275 0.3 |
0.2236069 0.2738614 0.3162279 0.3535535 0.3872984 0.4183301 0.4472137 0.4743418 0.5000001 0.5244045 0.5477226 0.5700877 0.5916080 0.6123725 0.6324555 0.6519203 0.6708204 0.6892024 0.7071067 0.7416198 0.7745966 |
0.22360679 0.27386128 0.31622776 0.35355339 0.38729834 0.41833001 0.44721359 0.47434165 0.50000000 0.52440443 0.54772256 0.57008772 0.59160799 0.61237243 0.63245553 0.65192025 0.67082040 0.68920245 0.70710678 0.74161985 0.77459668 | 4 5 6 7 8 9 10 |
4 4 4 4 4 4 4 4 3 3 4 4 4 4 4 4 4 3 3 |
0.325 0.35 0.375 0.4 0.425 0.45 0.475 0.5 0.525 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1.0 |
0.8062257 0.8366600 0.8600254 0.8944272 0.9219545 0.9486833 0.9746795 0.9999999 1.024695 1.048809 1.095445 1.140175 1.183216 1.224745 1.264911 1.303840 1.341641 1.378405 1.414213 |
0.80622579 0.83666005 0.86002543 0.89442719 0.92195445 0.94868331 0.97467945 1.00000000 1.02469505 1.04880886 1.09544514 1.14017546 1.18321595 1.22474487 1.26491107 1.30384050 1.34164081 1.37840491 1.41421356 | |