2. 数値積分の誤差
2.1 Simpson の積分公式の精度
. .
Simpson の 1/3 則積分公式の精度は O(h5)であるとされているが、これは積分結果が4次関数近似の精度であり、従って、被積分関数を3次関数で近似して積分したことに相当するということである。任意の3次関数の任意の区間[x0, x2]を求積法で積分した値と2等分点 x1 を用いて Simpson の積分公式で求めた値とは正確に一致するが、3次関数上のこの3点を通る2次関数の区間[x0, x2]を求積法により積分した値とも正確に一致する。従って、これら3点が任意の関数上の3点であれば、その関数を3次関数で近似しても2次関数で近似しても積分精度は同じであり、3次関数で近似する効果はない。更に、3次関数で近似しようとしても3点だけでは不定である。それなのに積分公式が被積分関数を3次関数近似した積分精度を持つというのは疑問である。
. .
x0,x1=x0+h,x2=x0+2h において y0,y1,y2 である3点を通る2次関数を次式で表して2区間を積分する。
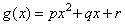 ___________(2.1)
___________(2.1)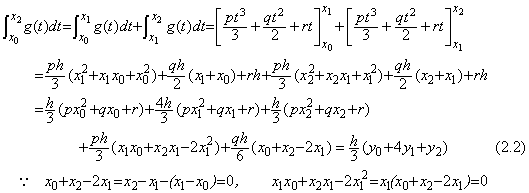
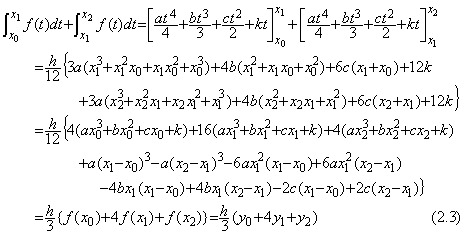
. . 例えば、被積分関数が指数関数(2.4)であるとき、3点 (0, 1), (1/2, √2), (1, 2)を通るから区間[0, 1]は2次関数(2.5)で近似でき、この近似関数の積分値は求積法でも Simpson の公式でも1.442809であり、真の積分値は1.442695……である。
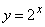 ___________(2.4)
___________(2.4)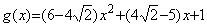 ___________(2.5)
___________(2.5)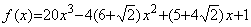 ___________(2.6)
___________(2.6)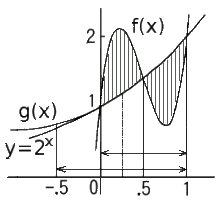 図 2.1 |
. . この第4点を区間[0, 1]の外、x=−0.5 における(2.4)上に取った3次関数は一意に確定し(2.7)で表される。
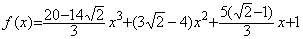 ___________(2.7)
___________(2.7)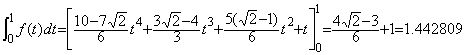
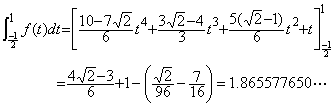
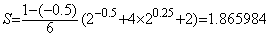
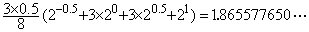
. . Newton の前進補間公式を2区間積分すると Δ3f0の項は消えるから剰余項はf(4)(x)で決まるということを前提として Simpson の 1/3則の剰余項は証明される。しかし、3点のみを与えられたとき、Δ3f0 は定義できないのであり、定義できないものを有ると仮定して剰余項を高次に設定するのは誤りである。3点のみ与えられた場合は Δ2f0 迄しか定義できないから剰余項は f(3)(x)を用いなければならない。中央差分を用いるものも定義できない奇数次項が消えることで剰余項を高次に設定する誤りを犯している。又、求積法で証明するものも、3次関数は3点のみでは一意に確定できないにも関わらず、できると仮定して剰余項を f(4)(x)に設定している上に、被積分関数に平均値の定理を適用し、それを積分したものが正しい積分になるという間違った計算をしている。これらは皆同じ結論に達するが皆同じ誤りを犯しているからであって正しいからではない。Simpson の 1/3則の正しい剰余項は第3章にて示す。
2.2 Taylor 展 開
. .
常微分方程式の数値解の精度検討に於いて Taylor 展開及びその Lagrange の剰余がよく用いられるが、理論的には(2.8)の x−a を必要なだけ小さく仮定し、必要なだけの次数を仮定できるので問題はなくても、実際の数値計算ではできるだけ広い区間を低次の関数で近似することが計算の簡単化と累積誤差を避けるために必要であり、このような数値計算の精度を Taylor 展開で論ずることは適当でない。剰余項は更に高次の微係数と積分の平均値を与える点 x=ξ を必要とするが、実際にこれらを計算するのは殆ど不可能であり、剰余項は零として近似しなければならないからである。
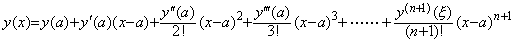 ___________(2.8)
___________(2.8)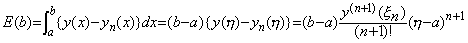 ___________(2.9)
___________(2.9). . (2.4)を n=2, a=0 で Taylor 展開すると、剰余項を R(n+1)で表せば、
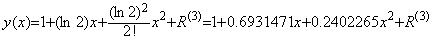 ___________(2.10)
___________(2.10)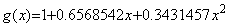
であるから係数は1桁しか一致しないし、g(x)は係数有効桁数と同じ7桁が真値と一致する2点(0.5, 1.414213), (1, 2)を通るが、y(x)の2次関数は真値と上位3桁しか一致しない2点(0.5, 1.406630), (1, 1.933374)を通り、近似精度が悪い。
. . (2.4)を n=3, a=−1/2 で Taylor 展開すると、
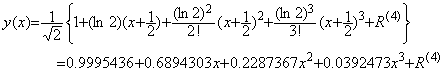 ___________(2.11)
___________(2.11)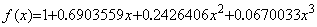
であるから高次の項の係数程不一致が著しく、f(x)は(0, 1)の他 g(x)と同じ2点を通るが、y(x)の3次関数はそれぞれ(0, 0.9995436), (0.5, 1.406349), (1, 1.956958)の3点を通り、やはり近似精度は悪い。
. . これら近似関数の 0.1 間隔の関数値を表 2.1 に、求積法による積分値を表 2.2 に示す。但し、上記 Taylor 展開の3次関数を区間[0, 1]で用いるのは定数項を見れば明らかなように、精度が悪すぎるので a=0 で展開した下式を用いている。
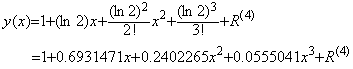 ___________(2.12)
___________(2.12)| 表 2.1_____近似関数値 (x の太字は区分点) | |||||
|---|---|---|---|---|---|
| x | Taylor 展開 | y(x)の3点を通る | 真__値 | ||
| 2次式 | 3次式 | 2次式 | 3次式 | ||
| 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 |
1.0 1.071717 1.148238 1.229565 1.315695 1.406630 1.502370 1.602914 1.708263 1.818416 1.933374 |
1.0 1.071772 1.148683 1.231063 1.319247 1.413568 1.514359 1.621952 1.736681 1.858878 1.988878 |
1.0 1.069117 1.145097 1.227939 1.317645 1.414214 1.517645 1.627939 1.745097 1.869117 2.0 |
1.0 1.071529 1.148312 1.230753 1.319253 1.414214 1.516036 1.625125 1.741880 1.866704 2.0 |
1.0 1.0717734 1.1486983 1.2311444 1.3195079 1.4142135 1.5157165 1.6245047 1.7411011 1.8660659 2.0 |
. . Taylor 展開の強い局所性は、展開点における関数の形を求めればよい数式計算では優れている。又、ただ一点の関数値を計算すればよい場合も展開点を近づけることができれば次数固定でも必要なだけの精度の解を得ることができるという利点もある。例えば、2次の Taylor 展開(2.10)で x=0.01 とすれば単精度で7桁正しい関数値を求めることができるし、更に x を小さくし2倍精度で計算すれば2倍精度の関数値を得ることもできる。常微分方程式の数値解法では Euler 法の精度がよい理由であるが、長区間の計算では区分点の数が膨大になること、一定区分幅では場所により局所性が著しく異なることにより大きな誤差を生ずる。被積分関数の高次微分が可能であれば広い区分幅でも精度のよい解を得ることはできるが、一般的には高次微分は簡単ではない。
| 表 2.2_____近似関数の積分値 (x の太字は区分点) | |||||
|---|---|---|---|---|---|
| x | Taylor 展開 | y(x)の3点を通る | 真__値 | ||
| 2次式 | 3次式 | 2次式 | 3次式 | ||
| 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 |
0.0 0.103546 0.214504 0.333354 0.460577 0.596653 0.742063 0.897287 1.062806 1.239100 1.426649 |
0.0 0.103547 0.214526 0.333466 0.460932 0.597520 0.743861 0.900619 1.068489 1.248204 1.440525 |
0.0 0.103399 0.214052 0.332647 0.459869 0.596405 0.742940 0.900162 1.068757 1.249410 1.442809 |
0.0 0.103534 0.214481 0.333385 0.460834 0.597451 0.743905 0.900901 1.069186 1.249546 1.442809 |
0.0 0.1035472 0.2145263 0.3334708 0.4609524 0.5975838 0.7440217 0.9009699 1.0691829 1.2494690 1.4426950 |
. . これに対し、p+1 点を通る p 次関数は Newton の p 次補間公式に等しくその精度が保証される区間は[a, a+ph]であることが明確である。Newton の補間公式は ph=x−a を固定して h→0 にすれば Taylor 展開に収束するから、h→0 を仮定した理論的な精度の検討では両者は同じであるが、h が有限の大きさである実際の数値計算の精度は大きな相違を生ずる。
2.3 局所相対誤差
. .
数値積分や常微分方程式の数値解法で用いられる積分公式は固定次数近似、固定区分幅であるのが常識的となっている。最近では自動区分幅調節の解法も行われてはいるが台形法や Simpson 等の低次の固定次数近似である。積分公式の精度は O(hp)と一般的に表されるが x の関数でもあり、被積分関数によっては x の影響の方が大きく1ステップの積分で有効桁がなくなるほどの誤差を生ずる場合がある。このような x の近傍では低次の固定次数近似の場合 h を極端に小さくする必要があり、一定区間の積分に要するステップ数が膨大となることにより大きな累積誤差を生ずる。
. .
連続関数 f(x)を任意の点 x0 から x1=x0+h 迄、台形法で積分する場合、f(x)の直線近似は、
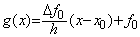 ___________(2.13)
___________(2.13)この積分を z(x)で表し、真の積分を y(x)で表すと、
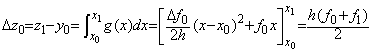 ___________(2.14)
___________(2.14)真値は、___________
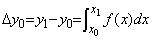 ___________(2.15)
___________(2.15)差分の相対誤差は、______
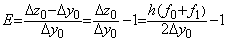 ___________(2.16)
___________(2.16)関数値の相対誤差は、______
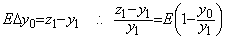 ___________(2.17)
___________(2.17). . 被積分関数が f(x)=−ae−x のとき、積分は微分方程式 y' =−y の解 y(x)=ae−x であり、
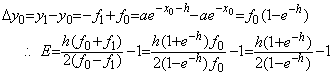 ___________(2.18)
___________(2.18)| 表 2.3___(2.18)の場合の z1 の局所相対誤差 | ||||
|---|---|---|---|---|
| y(真値) | f | z1 | (2.17)の値 | |
| x0=0 x1=0.1 |
10 9.04837 | −10 −9.04837 |
9.04758 | −0.876278×10−4 |
| x0=10 x1=10.1 |
4.53999×10−4 4.10795×10−4 |
−4.53999×10−4 −4.10795×10−4 |
4.10759×10−4 |
−0.876278×10−4 |
. . 従って、任意の x0 における近似積分 Δz0 の相対誤差 E は全区間に渡り一定で h のみにより決まり、h=0.1 ならば 0.8331945×10−3 であるから、Δz0 は全区間に渡って有効桁3桁となる。関数値 z1 の相対誤差は表 2.3 に示すように(2.17)により約 −0.105 倍になるから1桁精度は良くなる。固定次数固定区分幅解法でこの微分方程式が安定に解ける理由である。しかし、有効桁7桁の初期値で出発しても、次の区間は有効桁4桁の初期値で解かなければならないから台形法では精度はどんどん悪化していく。h=0.01 で E=0.8333319×10−5、関数値 z1 の相対誤差はこの約 −0.0105 倍になるから有効桁は7桁になる。従って、これより小さな区分幅にしなければならない。
. . 被積分関数が
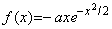 のとき、積分は微分方程式 y' =−xy の解
のとき、積分は微分方程式 y' =−xy の解
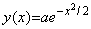 であるから、任意の x0 における真の積分 Δy0 及び近似積分 Δz0 の相対誤差 E は下記のようになり、h=0.1 のとき x0=0 における Δz0 の有効桁は3桁である。
であるから、任意の x0 における真の積分 Δy0 及び近似積分 Δz0 の相対誤差 E は下記のようになり、h=0.1 のとき x0=0 における Δz0 の有効桁は3桁である。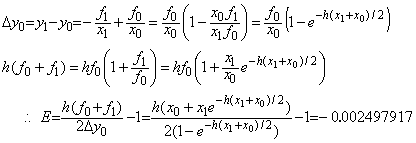 ___________(2.19)
___________(2.19)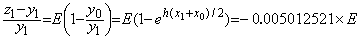 ___________(2.20)
___________(2.20)| 表 2.4___(2.20)の場合の z1 の局所相対誤差 | ||||
|---|---|---|---|---|
| y(真値) | f | z1 | (2.20)の値 | |
| x0=0 x1=0.1 |
10 9.95013 | 0 −9.95013×10−1 |
9.95025 | 1.25200×10−5 |
| x0=10 x1=10.1 |
1.92875×10−21 7.06007×10−22 |
−1.92875×10−20 −7.13067×10−21 |
6.07840×10−22 |
−1.39046×10−1 |
しかし、x0=10 では E=0.08028511、z1 の相対誤差も表 2.4 の値であるから Δz0 も z1 も真値から出発して1ステップで有効桁1桁しか得られない。1区間の積分精度を有効桁7桁にするためには h=0.001 とする必要があり、このとき E=8.084153×10−6、z1 の相対誤差は −0.01005067×E=−0.8125117×10−7 である。僅か 0.1 区間の積分に 100 ステップを要し、その積分値は 7.05997×10−22 で有効桁は5桁に減少する。
. . Simpson の 1/3 則を用いる場合には2区間を1ステップで積分するので任意の x0 に対する積分値の相対誤差は次式で表される。
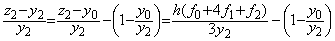 ___________(2.21)
___________(2.21). .
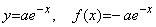 の場合は、
の場合は、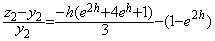 ___________(2.22)
___________(2.22)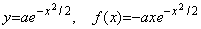 の場合は、
の場合は、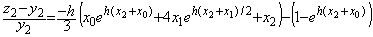 ___________(2.23)
___________(2.23). . 従来常識的となっている固定区分幅、固定次数の数値積分方式では、これ等の例に見られるように、常に正しい結果を得られることは保証されない。可変区分幅では著しいステップ数の増加を伴うので累積誤差を考慮しなければならない。それよりも可変次数とする方が精度の改善効果は顕著である。微分方程式の数値解法において、Runge K.法は安定であるが Milne 法は不安定であると言われるが無意味である。安定、不安定の問題ではなく、十分な精度の解を得るために必要な値に局所相対誤差を抑えることの出来る区分幅を用いているか否かの問題と、有効桁を失ったデータを生かしておく計算法に起因するものである。