第１章 数 値 解 法 の 諸 問 題
１． 数値計算の誤差と問題の誤差
1.1 誤 差 の 伝 播
. .
数値計算においては誤差を適切に評価することが重要であり、従来、誤差解析において用いられている評価法は過大評価である。又、常微分方程式の数値解に生じ異常な増大を示す誤差を打ち切り誤差では説明できないと結論し、誤差の伝播による拡大とか数値的不安定と説明することが常識的となっているが、これは重大な過ちを犯している。著者は、独自の並列計算向き数値解法を考案し、Milne 法で不安定現象を生ずる問題を正確に計算し得ることを示した。これら常微分方程式の数値解における難問と呼ばれる幾つかの例題について著者の解法を適用した結果は後に示すが、これらは適正な数値計算において誤差の伝播による拡大は有り得ないことを示している。物理学にポテンシャルエネルギー最小の原理というのがあるが、誤差の伝播による拡大という考えはこの原理に反している。誤差が拡大するのは外乱による、即ち、計算により新たな誤差が付加されるからであり、それがなければ初期のデータの誤差は計算により縮小する方向に向かうと考えるのが自然である。本節では主として誤差の伝播について詳細な検討を行なうが、従来の絶対値により定義される誤差の概念では十分な検討はできないので、本書では絶対値を付けず、符号付きで取り扱う。従って、
. . ある単精度実数A+ε とB+δ の積はAB+Aδ+εB+εδ であり、εδ は無視し得るから相対誤差の絶対値は和になり、従って、多数の実数の積を計算すれば|相対誤差|は拡大すると考えるのは誤差の見積もりとして安全ではあるが、過大な評価である。簡単のために、A, B>0 とすると、誤差が和になるのはε とδ が同符号の場合で、その確率は1/2であり、異符合の場合には誤差は差になり、その確率も1/2である。従って、相対誤差の絶対値の期待値は、
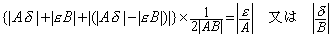
. . 適当に a, b を定め、yk=axk−1，xk=yk/a，x0=b；k=1,2,……,n の計算で n=106 等にすると log n に比例した桁数だけ精度が悪化するという議論が行われるが、切り捨て又は切り上げ計算ではそうなるが、４捨５入、16 進の７捨８入又は２進の０捨１入等が普通である現在の計算機ではこれは成立しない。電卓やパソコンで簡単に確かめられるが、同じ数を掛けて割れば元の値に戻り誤差は生じない。更に、このような計算を繰り返すことは数値計算として無意味であり、その誤差が何の様な挙動をしようとも誤差解析には無関係な机上の空論である。後に、演算子法においても述べるが、このような無意味な計算は本書の対象とする数値計算の範中には入れない。
. . 加減算は著しく誤差の拡大する場合もあり、注意を必要とする計算であるが、それは新たに誤差が付加されるか、潜在的な誤差が現れるのである。又、乗除算の場合と異なり拡大した誤差が著しく減少し元の精度に戻ることもある。
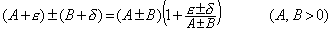
. . 減算の場合には相対誤差計算の分母が小さくなるので結果の相対誤差は拡大され、ＡとＢの値が近い程拡大倍率は大きくなり、最悪の場合には有効桁がなくなる。このいわゆる桁落ち誤差が伝播により異常な拡大をすると現時点でいえる唯一のものであり、２次方程式の根の計算や、連立１次方程式の解の計算においてはその解決法も考えられているが、一般的には解決法はない。しかし、桁落ちしたものにそれより絶対誤差の大きな単精度実数が加減算されゝば上記の実例の如く精度は一挙に単精度迄改善されるので複雑な計算程桁落ち誤差も伝播しない可能性が大きい。このような例は微分方程式の数値解にはよく現れる。例えば、解が ｘ 軸と交叉するとき、交点の近傍では零に近づくため桁落ちして精度が悪化するが、交叉後 ｘ 軸の反対側に離れるに従い精度は改善される。解が ｘ 軸に漸近する微分方程式、
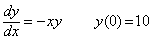___________(1.1). . 以上は計算に丸め誤差が入らないことを仮定して数値の持つ誤差の伝播を検討したが、１回の計算で入る丸め誤差は末尾桁に１であり、この誤差のその後の挙動は上記に述べたものと同様である。従って、従来の誤差論が主張するように一般的には単純に誤差が累積することは期待しがたく、著者の微分方程式の数値解法が示すように複雑な計算である程、丸め誤差も又伝播はしないといえる。
1.2 情報落とその改善
. .
情報落ちは何度も続けておき、累積される場合以外は直接計算精度の悪化にはならないが、単精度実数AがBより桁違いに大きいので
. . 第１の方法は、数式計算の結果、即ち、Bを直接用いることである。２次方程式の小根を求める際の逆有理化はこれに相当する。根の公式の−b と b2−4ac の平方根とがこの関係にあり、両者の和を各々の２乗の差に変換して b を相殺したものであるが、
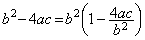
. . 第２の方法は、A及びBの末尾に 0 を数桁付けて多倍長精度数とし、多倍長精度計算をすることである。こうすれば情報落ちが起きないので(1.2)は等式が成立し正しい結果となる。２次方程式の根では各係数末尾に0 を数桁付けて多倍長精度数とし、多倍長精度で平方根を求めれば逆有理化は必要ない。この方法は必要なだけの多倍長計算が可能である限り有効な方法である。しかし、倍精度計算では倍精度長の結果を得たいと思うのが計算の手間やハードウエアの制約から冗長性を嫌う計算機の分野では普通であり、部分的に倍精度長を用いるのも、２次方程式のようにそれを必要とする計算式が明確である場合以外は困難である。
. . 第３の方法は、情報落ちが生じたときは自動的に情報落ち部分を他の変数に累積していく、いわゆる積み残し法を用いることである。このとき計算に切り捨て等の丸め誤差が入るときはその補正分も積み残す必要があり、一般計算における単純な積み残し法は困難である。
. . 常微分方程式の数値解法において、従来の解法では y0, y1, y2, y3, …… という関数値を直接計算するのに対し、著者の解法は逐次階差 y0, Δy0, Δ2y0, Δ3y0, …… を直接計算し補間公式により関数値を求める。Δy0=y1−y0 で求めた階差は区分幅が小さいとき桁落ちして有効桁が減少し末尾桁は 0 であるが、著者の解法では常微分方程式の右辺の関数より直接計算されるので末尾桁も有効な情報を含んでいる。y1=y0+Δy0 の計算で y0>0 かつ Δy0<0 による減算のとき、Δy0 の絶対値が y0 に比べて十分小さくても、y0 の最上位桁が 1 で下位桁からの借りにより最上位桁が失われる桁落ちがある。微分方程式の数値解が零に漸近する場合はこのようにして最上位桁が失われていくことによるものである。そのとき最下位桁に補うべき情報、即ち、積み残し分を著者の解法による Δy0 は持っている。同様に、Δ2y0 は y2 の計算に必要な Δy1 を計算する際の積み残し分を持っている。この様に著者の解法は積み残し法を構成しているのであり、それが従来の解法では到底及びもつかない高精度と安定性を持っている１つの理由であり、逐次階差を直接計算する意義である。
1.3 問題の数値化精度
. .
２次方程式 ax2+bx+c=0 の数値解を求める際に係数をある精度で数値化するが、解の計算で誤差が入ると係数の数値化精度を悪化させたことと等価になる。単精度が 10 進５桁の計算機を仮定し、一般性を保つために解も係数も無限少数となる次の２次方程式を数値解法で解く場合を考える。a=1 としても一般性は失われない。
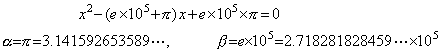______(1.3)
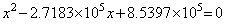___________(1.4)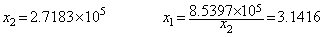
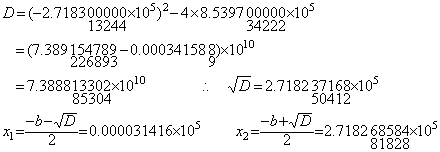
. . 単精度計算で小根が x1=0 となるのは計算の途中結果を全て単精度に丸める計算の仕方が悪いのであり、(1.4)は(1.3)を 10−5 の精度で数値化近似しているということができる。しかるに、途中計算を単精度に丸めることにより判別式の平方根の計算で 4ac が無視されたことに相当する計算結果になるのは c が無視されたことと同じであり、方程式を(1.5)に変えたことになる。この２次方程式の根は(1.4)を単精度計算した根と同じである。4ac の一部が情報落ちするときはそれに相当する ｃ の末尾桁が失われた方程式に変えられたのと同じである。即ち、途中計算を単精度に丸めることは、この場合、方程式の数値化の精度を悪化させたことになるのである。
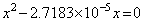___________(1.5). . 連立１次方程式、(1.6)の係数を単精度５桁で近似すると(1.7)となる。
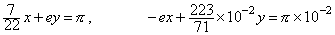___________(1.6)
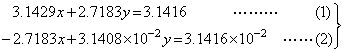___________(1.7)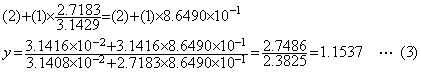
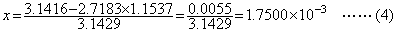
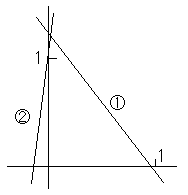 図1. 1 |
. . ピボット選択が必要なのは解の一方が極端に小さい場合であり、そのとき図1.1 の様に一方の直線が大きい方の解の座標軸と極端な鋭角を成すときこのような問題が生ずる。２元の場合には(2)式を 100 倍した表記を用いればその x の係数が絶対値最大となるので解決するが、多元の場合にはこの様な解がいくつも有り得るので消去の過程で上記(1)と(2)の関係が生ずるのを避けることはできない。
. . 連立方程式の解法としては(3)の計算で求めた y を(1)ではなく(2)へ代入してもよいのであり、その場合は下記のように有効桁５桁の x を得る。
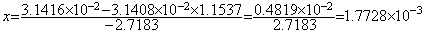
______(1.8)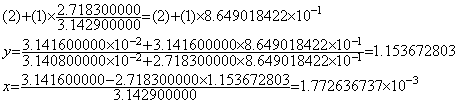
. . ２直線が各座標軸と十分な角度を持ち解が各座標軸から十分離れていればこの様な問題は生じないが、両直線が鋭角に交わるときは別の問題が生ずる。
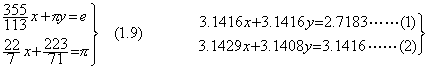_____(1.10)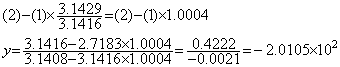
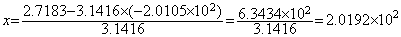
. . (1.10)の各係数の末尾に零を５桁付けて２倍長精度で計算すると、
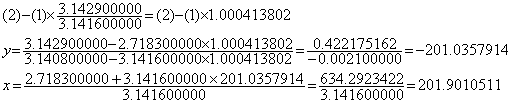
. . この(1.10)の正しい解が(1.9)の真の解と有効桁２桁でしか一致しないということは方程式自体の数値化近似の精度が 10−2 でしかないということであり、この誤差は問題自身の数値化の誤差で、解の計算途中に生ずる計算誤差ではない。この２直線は各 ｘ, ｙ切片がほゞ１で交点はその 200 倍も遠方という極めて鋭角な交叉をしていて、(1.10)の各係数の末尾桁が１ 異なるだけの僅かな切片または勾配の誤差で交点は大きく変わるから係数を５桁で近似した(1.10)では交点を有効桁５桁で求めることは不可能なのである。従って、係数を有効桁５桁で近似しても方程式が 10−5 の精度で近似出来たとは限らないのである。著者はこれを問題の数値化近似の精度と呼び、それが 10−2 であるという。
. . ２次方程式では近接２実根または虚数部の小さい虚根を持つとき、即ち、その左辺の２次方程式の頂点が x 軸に極めて近いとき、２実根か等根かあるいは虚根であるのかの判定が困難となり、正しく判定できる場合も根の精度は悪化することはよく知られている。判別式に桁落ちが生じ(1.2)に相当する情報落ちがないので桁落ちを補う手段 がないからである。
. . 虚根 π±je×10−3 を２根とする２次方程式(1.11)を単精度５桁で近似すると(1.12)となるが、π2=9.869604…… であるから定数項が e2×10−6 を含んでいないし、x の係数も e×10−3 を含んでいないので真の解を求めることはできない。係数を有効桁５桁で近似したのでは問題の数値化近似の精度が悪すぎて(1.13)の近似式と区別ができないのであるが、更に、(1.12)から(1.13)の重根 πを求めることもできず、下記の計算に示すように２実根となる。
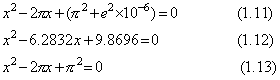
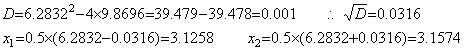
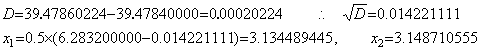
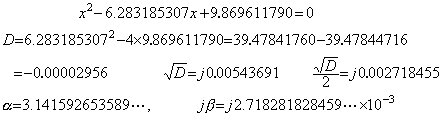
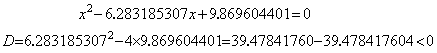
. . この誤差は計算の誤差ではなくて問題自身の数値化近似の際に設定されていた誤差である。このことは(1.12)の左辺の関数値を計算した表1.1 を見れば明白である。途中結果を全て５桁に丸める計算では頂点の近傍はでたらめであるが、丸め誤差の入る桁を 10 桁目にするため係数末尾に零を５桁補って 10 桁計算した場合は上に求めた２根で ｘ 軸と交叉し、x=π のあたりに頂点がある様子がわかる。しかし、関数値は真値である(1.13)の左辺の値とは著しく異なっている。微分値は多少精度がよいが関数値の精度が悪いのでNewton-Raphson 法でも真の根を求めることはできない。
| 表 1.1_____y=x2−6.2832x+9.8696 と dy/dx | ||||||
|---|---|---|---|---|---|---|
| x | ５桁計算 | 10 桁計算 | 真___値 | . | dy/dx | 真___値 |
| 3.1100 3.1200 3.1300 3.1350 3.1400 3.1450 3.1500 3.1600 3.1700 |
0.0007 0.0000 0.0005 −0.0002 0.0002 −0.0004 0.0001 0.0002 0.0006 |
0.000948 0.000416 0.000084 −0.000007 −0.000048 −0.000039 0.000012 0.000288 0.000756 |
0.000998095 0.000466242 0.000134389 0.000043463 0.000002536 0.000011610 0.000070683 0.000338830 0.000806977 | −0.0632 −0.0432 −0.0232 −0.0132 −0.0032 +0.0068 +0.0168 +0.0368 +0.0568 |
−0.063185307 −0.043185307 −0.023185307 −0.013185307 −0.003185307 +0.006814692 +0.016814692 +0.036814692 +0.056814692 | |
. . この様な桁落ちは ｘ 軸の近傍における関数値の計算の際に生じ、微係数が零に近いとき著しく、表1.1 に示すように２次関数では頂点が ｘ 軸の近傍にあるとき頂点の近傍の関数値や微係数は普通の方法では正確に求めることができないし、関数が ｘ 軸に漸近するときも同様である。これは数値微積分や微分方程式の数値解に著しい誤差を生じ、微分方程式(1.1)の数値解の計算で、Runge K. 法における著しい誤差や Milne の解法に生ずる不安定現象と呼ばれる現象の大きな原因となる。
. . 問題の数値化の精度が正しい解を得るために十分な精度であっても、数値計算が正しい解を得るためには(1.2)の関係は等号である、即ち、(A+B)−A=Bが成立しなければならない。そのためには、データは単精度でも計算は情報落ちを起こさないために必要な桁数の多倍長計算でなければならない。単精度データを２倍長計算するのは誤差論的に意味がないという誤った計算論と、初期の計算機のメモリやレジスタにおける制限から単精度データは単精度計算で十分という考えが常識的となっている。それが上記に述べたような計算誤差や微分方程式の解の暴走原因となっている。これはディジタル計算機を用いた自動制御機器は暴走する危険性を持つことを意味する。しかし、必要なだけの多倍長計算も実用上は難しく、計算桁数の制限はやむを得ない。このとき有効桁を失ったデータを生かしておく従来の計算法に大きな問題がある。データは数値とその有効桁数を常に対にして四則演算し、有効桁数が零になったときは数値も零にクリアしなければならない。固定小数点演算のときは自動的にこれが行われていた。アナログ計算機やアナログ自動制御機器も増幅素子の閾値によりそれより小さな信号は増幅できないことで自動的にこれが行われていた。今の浮動小数点演算は、浮動小数点数は幾らでも小さい数値を扱えるから閾値がなく正確な計算が出来るという間違った議論に基づいている。それが可能であるためには丸めの起きない桁数の計算が出来なければならない。