8. 太陽までの距離を測定する
. .
南北に十分離れた2地点では日南中高度(正午に南方に見た太陽の角度)が異なる。大地は平面であると考えていた古代エジプト人はこの2点間の距離と両底角で決まる三角形の頂点に太陽が有ると考えた。実際にはこの頂点迄の距離は太陽が北回帰線上に有るとき地球の半径にほぼ等しいのであるが、大地が平面であると考える彼らには太陽迄の距離であることは疑う余地の無いものである。現代人はこの距離を計算するのに三角関数を使用するが、彼らは三角関数は知らないけれどもこの距離を簡単に計算することが出来た。其は前節で述べた円弧長1°Lに対する半径57°17'48"Lの関係を使用し、1°Lを2点間ABの実測距離から求めるものである。
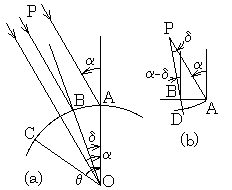 Fig. 8.1 | . . |
太陽が北回帰線にあるときθ−α=23°27'であるから、ファイユーム(北緯29°19')の近辺Aでα=6°となり、そこから太陽の角度α−δ=5°、即ち、δ=1°となる地点B迄の距離を測れば、太陽迄の距離APは地球の半径をRで表わして以下のようになる。
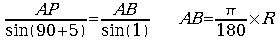 | . .故に、 | 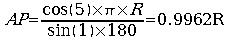 |
. . ABの距離は実際に測量して得られ、地球の子午線の半径は6357kmであるから、その円の中心角1°に対する円弧長6357×π÷180=110.95kmである。上記のABを110950倍すればAPも110950倍になり、そのABを3614で割ればAPも3614で割ればよいからAP=206268×110950÷3614=6332439m、即ち、古代エジプト人の求めた太陽迄の距離(地球の半径)は6332kmとなる。この計算値は、先に述べた三角関数を用いた計算値であるAP=0.9962×6357=6332.8kmと比べれば十分精度が良い。
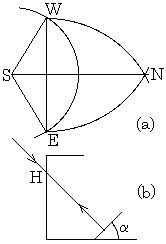 | . . |
. . 日南中高度が同時刻に1°高い位置を求めるには、線分SNの延長線上の100km以上離れた地点を計測しなければならない。この計測には前節で求めた円弧長1°Lと半径の関係及び太陽光線を用いる。地面を上から見たFig. 8.3にその測定原理を図示する。中心がOで直径がSNである円の中心角NOQ=2δの円弧上のNに鏡を線分SNと直角に置き、Qにもう1つの鏡を線分SQと直角に置く。平行光線PQとSN及びそれらの反射光は図の角度となり、両反射光は中心Oで交叉する。故に、NQの距離を1°Lに設定しておけば中心角NOQは2δ=1°であり、半径NO=57°17'48"Lである。
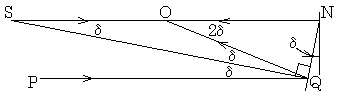 | . . |
9. 太陽迄の距離の修正
. .太陽が北回帰線にあるときFig. 8.1のα=6°の地点Aは北緯θ=29°27'であるから、太陽が南回帰線にあるときはα=θ+23°27'=52°54'である。α=51°54'の地点B迄の距離は地球子午線の中心角1°の円弧長110.95kmで変らないから、太陽迄の距離は、
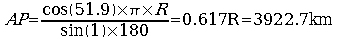
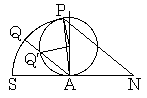 Fig. 9.1 | . . |
. . 彼らは太陽がそのような円弧を移動するのは大地に隈無く恵みをあたえるためであり、従って、太陽は夏にはエジプトの真上まで来るのであるから太陽がQに有るとき光線QAに垂直な斜面が遥か南方に存在すると考えた。其れが地球という球面の一部であることを知らなかった彼らは、その斜面はエジプトの大地と何処かで交わっており、QAの正しい距離はその斜面において前節に述べた計算をしなければならないと考えた。その値は太陽がエジプトの真上にあるとき計測する必要があるが、その地点はアスワン近辺の山岳地帯であり計測は困難である。しかし、その値はFig. 8.1(b)の二等辺三角形APDの角DがBに重なるように回転したときのPAの距離を計算すればよい。
. . このとき、円弧長AD=AB=1°L=110.95kmの半径はAP=57°17'48"Lである。即ち、AB=3600"L、AP=206268"Lである。ABを110950倍すればAPも110950倍になり、そのABを3600で割ればAPも3600で割ればよいから、
10. キュービットとインチの絶対不変の単位長の発見
. . 古代エジプト人は太陽の1回転である1日という周期と1461回転の4年という長周期に関して特別な考え方をしていた。太陽が1回転で走行する距離は360°Lであり、2回転で走行する距離は720°Lであるが、これは2倍の半径の円の円周長に等しい。従って、2回転毎に起こる周期現象は2倍の半径の円を回転するのと等価な現象である。故に、太陽が4年、即ち、1461回転を周期としていることは1461倍の半径の円を4年に1回転しているのと等価である。Fig. 8.1のα=6°の地点Aは北緯θ=29°27'であり、大地がこの地点で水平な平面であるなら、太陽はFig. 10.1に示すように大地に対して60°33'の角度で回転している。
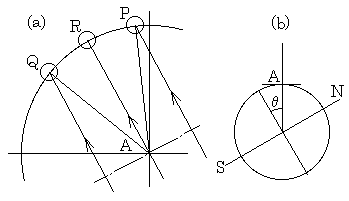 Fig. 10.1 | . . |
. . 一方、太陽の南中における回転角度の測定精度の向上により、その角度は45°ではなく46°54'であることが知られた。この区間の円弧を4年に4往復すると375°12'回転することになるが、これでは季節の周期と大きくずれることになる。彼らは、大地には表と裏があるので表の大地は太陽の回転中心を通る水平線より高い位置にあり、見かけの太陽の回転角度は大きく観測されると考えた。この考えは後にピラミッドの高さを決定する。実際には、太陽の南中における回転は6357kmの半径の円弧45°の部分を1年に1往復しているので4年間の南中における回転の走行距離は半径6357kmの円を1回転する円周長に等しく、そのために4年、即ち、1461日を必要とすると考えた。この円の中心角1°の円弧長が第8節で太陽迄の距離の計算のために実測した110.95kmである。一方、東西方向の回転は6357kmの1461倍の半径の円を1461日で1回転しているのと等価であり、両回転は1回転毎に完全に同期している。従って、太陽の南中における回転円の中心角1°の円弧長と東西方向の回転の6357km×1461の半径の円の中心角1°の円弧長とは等価であると彼等は考えた。古代エジプト人は絵画技法に見られるように立体視が不得手であったのでFig. 10.1に示すような大地に対して斜めに回転する場合の回転角度や回転周長を測定することが出来なかった。そこで彼らはこのような方法で太陽の東西方向の1日の回転の中心角1°の円周長を求めようと考えたのである。
. . 故に、太陽が1日に1回転する円の中心角1°の円弧長1°L、及び、1'Lの長さは、
| 1°L=110950÷1461=75.9411m=75m94cm |
| 1'L=7594÷60=126.57cm=127cm |
. . キュービット(腕尺)は掌を伸ばした中指の先端から肘までの長さであり、古代エジプト、バビロニア、イスラエル、ギリシャ、ローマなどの尺度であるが、この長さは人により異なるから国によって異なり、イスラエルが最も短くて45cm弱、エジプトが最も長くて約52.4cmとされる。このキュービットで太陽までの距離を計算したとすると、太陽の南中高度が1°異なる区間の実測値110.95kmは211736Cubit 16inchとなる。従って、太陽が1日に1回転する円の中心角1°の円弧長1°L、及び、1'Lは、
| 1°L=211736Cubit 16"÷1461=144Cubit 23" |
| 1'L=144Cubit 23"÷60=2Cubit 10.38"=2Cubit 10"2/5 |
. . この古代エジプト人のキュービットの定義は現代における長さの単位の定義と同じである。第8節で太陽迄の距離の計算のために実測した110.95kmは地球子午線の中心角1°の円弧長であるから、任意の単位で測った地球の半径をRとすれば 2πR÷360 であり、これが太陽が1日1回転する円の中心角1°の円弧長1°Lの1461倍に等しいから、
故に、 1Cubit=πR÷31557600=R÷10045096
. . インチという単位はもっと古い時代、1日が24時間と定められた時代に定められたと考えられる。この時代には1回転の角度も24時間であった。彼らは24と言う数値を繰り返しの単位(周期)と考えていたので1キュービットも24インチと定めた。彼らの知る数値は1から始まる整数のみであるから、1日が4つの時刻に分けられたとき1日の始まりである日の出を1の時刻、夜中を4の時刻と定めた。やがて彼らは1日の始まりは4の時刻であり、その日最初に訪れる時刻が1の時刻で、その日の終わりが4の時刻であることに気が付く。1日が24時間でも同様に、1日は24の時刻に始まり最初に訪れる時刻が1の時刻で、1日の終わりが24の時刻である。彼等は0と言う概念を知らなかったが、回転の角度を表す場合はこのように最大値を記した目盛が始まりの目盛で差し支えなかった。しかし、直線を測る定規の場合、0インチを示す目盛に24と記すのは変であるので1を記した。従って、24インチを示す目盛には25と記した。この目盛が1キュービットの目盛であり、次の1キュービットをインチで示す最初の目盛1となる。しかし、やがて彼らはキュービットの単位は1の目盛の前に始まりの目盛があるのにインチの単位にはそれが無いのはおかしいことに気が付く。そこで両単位に共通の始まりを表す記号を考案して最初の目盛に付けた。従って、目盛の数値は1目盛後ろにずれて24インチの目盛に24と記され、25の数値は消えるのであるが、これも1目盛ずらして残してしまった。その結果、25インチが1キュービットになってしまったと考えられる。但し、始まりの目盛が1であったとき、25番目の目盛が1キュービットであるという記述を25インチが1キュービットであると後世の人間が誤り解釈したとも考えられる。
11. 1年は365.2422日であることの発見
. .
現在の太陽暦では1年を365日とし、4年に1度閏年をおいて366日としているが、更に精度を上げるために400年毎に3回ずつ閏年を平年に戻す調整をしている。従って、閏年は400年毎に97回あり、400年=365×400+97=146097日である。400年間の平均は1年=365.2425日となるが、更に正確には1年=365.24219日であることが知られている。400年毎に閏年が100回では補正量が3日多過ぎ、133.3年で1日、33.3年で1/4日多過ぎる。前節迄に述べた古代エジプト人の角度測定技術からすればもっと短い年数でこのずれを観測することは出来たが、それが何時間何分何秒であるかを正確に決めることが出来なかった。その理由は、日の出の位置は単振動、即ち、sin関数に従っていて等間隔でないからである。しかし、1/4日のずれは1年間のずれとして観測できており、33年観測すればこの補正のずれを観測できる。又、33年という年数も一人の研究者が一生をかけて研究を達成することの可能な期間であり、彼らはこのずれを計測できた。
. .
赤道で地球と交わる平面とエジプトで水平な平面の交線の東方から太陽が昇ったときを1年目の初日の出とし、その日の出位置をS0とする。太陽が螺旋状の回転をしながら南下して南回帰線に達し、北上して北回帰線に達し、再び南下して赤道で地球と交わる平面に達したときが正確な1年であり、この間に太陽は365.24219回転する。1年を365日とすると2年目の初日の日の出位置は太陽を0.24219回転戻した位置であり、この位置をS1とするとS1とS0の間隔は0.24219日を示す。古代エジプト人はこの値を知らなかったからこの間隔は約0.25日であると考え、4年に1日の閏年を設けた。しかし、この補正では日の出位置は次第にずれていくことが観測された。
. .
32年間に0.25×32=8日を加算すれば33年目の初日の日の出位置は出発点に一致する筈であるが、実際は(365+0.24219)×32=365×32+7.75008日で太陽は赤道で地球と交わる平面に達する。33年目の初日の日の出は太陽が更に0.24992回転したときで、その位置をS32とするとその位置は出発点の南にあり、S0とS32の間隔は0.24992日を示す。彼等はこの値も知らなかったが、この値はS1とS0の間隔より大きいことは三つの目印間の角度を測定して知ることが出来た。又、この値は0.25日より大きい筈はないから彼等はこの値を0.25日と仮定した。彼等は知らなかったがこの仮定は極めて精度がよかったのである。この結果、太陽は32年間に365×32+7.75日回転するから1年の平均日数は、
. . この補正で33年間は(365+0.2421875)×33=365×33+7.9921875日であり、実際の太陽の回転数の加算分も0.24219×33=7.99227日であるから、この補正は実際と極めて良く一致する。彼等は実際の太陽の回転数の加算分を知らなかったが、このことは34年目の初日の日の出位置がS0と殆んど一致することで確認できた。そこで33年間の補正日数を8日とすると8÷33=0.242424日=5時間49'5"となり、少数表示では大した違いではないように見えるが、彼等の整数計算は時間表示であり20"の違いは無視出来なかったであろう。しかし、彼等は33年間の補正日数を8日に丸めるのは正しくないことを知ることが出来た。33年間の太陽の実際の回転数は365×33+7.99227回転であるから34年目の初日の日の出位置はS0より南側に0.00773日分過ぎた位置であり、この違いは明確に識別できた。一方、計算上の日の出位置は0.0078125日分過ぎた位置であり、実際の日の出位置との違いは識別できなかった。
. . 太陽の日の出位置はsin関数に従うから出発点S0より0.25日ずれた日の出位置は振幅をAとすれば、A•sin(0.25×2π÷365)=0.0043Aであり、Aは太陽が南回帰線にあるときの日の出位置とS0の間隔で視角にして約30°であるから0.0043A=7'44"となる。角度の単位が秒迄しかないので彼等の測定可能な最小視角を1秒とすると、1"÷7'44"=0.002の精度となる。従って、0.25日を測定したときの精度は0.0005日であるから0.00773日は十分に識別できる。しかし、0.0078125−0.00773=0.0000825日は識別できない。
. . 季節の変化は太陽の南中における高度と同期して変化しているのであるから、1年と言う周期はこの高度の変化と完全に同期しているのであり、太陽の南中における1年間の移動距離は前節で述べたように半径1000万キュービットの円の中心角45°の円弧長45°Lを1往復する距離であることは変わりがない。従って、上記の補正が必要な理由は単純に太陽の東西方向の回転角度が4年間の観測結果1461日より僅かに少なく、1460日23時間15'4"であることによる。そして太陽は32年よりもっと長い周期で回転していることになる。その周期を整数計算で求めるには秒、分、時間を順次零にする最小の整数を掛けて以下の様に求められる。但し、y=year, d=day, h=hourである。
| 1y=365d5h48'46" . . 30y=30×365d+7d6h23' 60×30y=60×30×365d+365d+70d+23h 24×60×30y=24×60×30×365d+28×365d+243d 24×60×30y=1440×30y=43200y=15778463d |
| 目 次 へ | 次 へ |