4. 一回転は何故360度か
. .
1回転、即ち、24時間は2等分、3等分、4等分、6等分は出来るが5等分が出来ない。彼らは其を可能にする角度の単位が存在する筈であると考えた。又、任意の角度を2等分、4等分することは簡単に出来るが、3等分、5等分、6等分は出来なかった。しかし、彼等はやがてその作図法を発見する。勿論、其は近似画法であるが、彼等の計測技術では真値との有意差を見出すことは出来ない程精度が良く、且、簡単な方法である。其については後で述べるが、彼等はこれにより1時間を5等分して、其の4つの角度と4時間を加えた角度により24時間が5等分出来る、即ち、(4+4/5)×5=24であり、正五角形が作図出来ることを知る。従って、1回転の角度が120となる角度の単位が存在する。しかし、其を時間の単位として使用した場合、現代の12分であり、古代エジプト人の日常的な作業を測る単位としては短すぎて不便である。その結果、時間の単位と角度の単位は分離することになる。時間の単位は1日が24時間となる太陽の回転角度であり、一般的、幾何学的な角度の単位は1回転が120となる角度となる。
. .
次に彼等は正六角形を検討したが新たな単位は生まれなかった。1回転の角度120は20の角度6個に分けられ、各内角は40、外角は20であり、正三角形や正四角形との間で構成される全ての角度に端数は生じない。又、1/6の角度の単位が存在したとすれば1回転は720となり太陽の1年の回転数のほぼ2倍となる。従って、これ以上の正多角形による新たな角度の単位は生じないと彼等は考えたが、やがてこの単位では表わせない不変固有の角度の存在を発見する。太陽が最も北に来たときの正午における垂直に立てた棒の影と太陽光線のなす角度を測定し、太陽が最も南にあるとき其の角度を測定すると、その差は角度15と16の間で角度1の2/3程であることである。この角度は46°54'であるが、当時の計測技術ではこの精度は得られず、これは整数で表わされると考えられ、それには角度1を3等分する単位が必要であり、1回転の角度は360となると考えた。この値は太陽の1年の回転数365に極めて近く、又、太陽が5回転を必要とする理由も第2節で示したように説明がつく。故に、1回転の角度は360度と決定される。
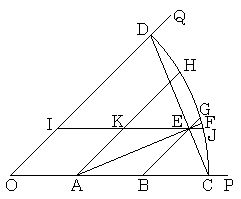 | . . |
| Fig. 4.1 |
| [角度を3等分する方法] | |
| 1. | ∠POQが与えられたとき、線分OP上に等間隔に3点A, B, Cを取り、Oを中心として半径OCの円弧CDを描く。 |
| 2. | 線分ODに平行な線分BGと弦CDの交点Eを求め、線分AEの延長線が円弧CDと交わる点Fを求める。 |
| 3. | 線分OFを引けば∠POFは∠POQの非常に精度の良い3分の1である。 |
. . 実際に、CADを用いて45°を3等分する角度を作図してCADで測定してみると、半径OCが300mmの図形を描いたとき15.17°を得、精度は約100分の1である。1時間の角度、即ち、15°を3等分すると5.006°を得、精度は約1000分の1である。この誤差を粘土板や地面に描いた図形で検出することは困難であろう。
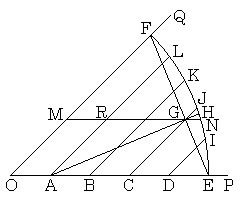 | . . |
| Fig. 4.2 |
| [角度を5等分する方法] | |
| 1. | ∠POQが与えられたとき、線分OP上に等間隔に5点A, B, C, D, Eを取り、Oを中心として半径OEの円弧EFを描く。 |
| 2. | 線分OFに平行な線分CJと弦EFの交点Gを求め、線分AGの延長線が円弧EFと交わる点Hを求める。 |
| 3. | 図示は省略されているが、弦EHを半径として、Eを中心とする円弧とHを中心とする円弧の交点Sを求めれば∠POSは∠POQの非常に精度の良い5分の1である。 |
. . 実際に、CADを用いて45°を5等分する角度を作図してCADで測定してみると、半径OEが300mmの図形を描いたとき9.055°を得、精度は約1000分の6である。1時間の角度、即ち、15°を5等分すると3.002°を得、精度は約10000分の7である。この方法で正五角形を作図するとき、5時間の角度を作図するときの誤差は理論的には零であり、其から1時間の1/5、即ち、3°を減ずる作図の誤差は0.002°であるから、この正五角形の作図精度は0.002÷(15×5−3)=0.000028となり、10万分の3である。実際には作図作業上の誤差が有るからこの精度は得られないが、古代エジプト人が正五角形の存在を確信するに十分な精度の正五角形を作図できるであろう。
5. 水の沸点と氷点の温度差は何故180°か
. .
華氏温度は1714年にドイツ人物理学者ファーレンハイトが制定したと言われるが、このとき既に、水の氷点を180°、沸点を0°とする現在とは数値が逆表示の温度計測が行なわれていた。彼はこの関係を逆にして水の氷点に32°のバイアスを着けたのである。その証拠は28年後に制定された摂氏温度に有る。1742年スウェーデン人セルシウスは摂氏温度を制定したとき、水の氷点を100°、沸点を0°と現在とは逆に設定した。10進法では基準となる量は0, 10,
. .
彼等は温かさを数値で表わそうと考えたとき矢張り太陽に注目した。朝、太陽が現われると温かくなり、角度が増すと温かさも増し、正午を過ぎると温かさは減少していき、日没以後は寒くなる。従って、温かさは太陽の回転角度で表わすことが出来る。しかし、温かさは正午に対して対称であるから時間と異なる角度測定基点が必要である。彼等は地面に垂直に立てた棒の影が温かさと同じ変化をすることを知っていた。朝、西方に長い影を作り、正午に最短となり、日没時には東方に長い影を作る。これと同様に、温かさは正午に最も小さい角度で表わされ、夕方には角度を増し、夜中には180°に達し、以後角度を減じて正午の角度になると彼等は考えた。しかし、正午の温かさも夜中の寒さも影の長さと同様に季節により大きく変るから、角度の始点0°で表わされる温かさと180°で表わされる寒さは他の固有の熱さ、冷たさに設定するべきであると考えた。彼等は0と言う数値を知らないが、何もない、或いは、始まりという概念は持っていた。これを説明の都合上0°と言う表記を用いて表す。
. .
彼等の知る最も熱いものは火であり、気化熱と言う概念を知らない彼等は水を火で熱したとき沸騰すると温度が一定になるのは火の温度に達したからであると考え、このときの温度を0°と定めた。又、彼等の知る最も冷たいものは自然に出来た氷であり、これを火で熱すると氷の残っている間は温度が一定であるのは其が氷の温度だからであると考え、このときの温度を180°と定めた。この温度表記は日常起こり得る氷点下の温度もマイナスと言う概念を使わずに表記でき便利であるので華氏温度の制定まで使われることとなる。マイナスと言う概念は紀元5、6世紀にインドで確立されヨーロッパに伝わったとされるが、一般的に使用されるのは摂氏温度制定以降と考えられる。
. .
1760年頃より産業革命が始まった。従って、1700年頃には水の沸点よりも遥に高い温度の計測が必要とされた。そこでファーレンハイトは温度が高い程数値が大きくなるように、水の氷点を0°、沸点を180°と温度表示を替えようと考えた。しかし、冬には日常氷点化の温度になり、マイナスと言う概念が一般的でない当時、この温度を表示するためには水の氷点より低い温度を0°に設定する必要があった。その温度は日常の気象条件では起こり得ない温度に設定すべきと彼は考え、その温度を水の氷点よりも32°低い温度に設定したのであるが、物理学者である彼は人間の体温のような個人差や変動のあるものを基準にしたのではなく、もっと科学的な根拠を持って決定してる。彼は固有の氷点を持つ液体から通常の気象条件では凍らない液体の氷点を推定し、水の氷点より32°低い温度を得た。従って、これより低い温度は存在しないと彼は考えた。実際に、人工的な冷却装置のない当時、彼の居住する地域においてこのような低温になることは無かっただろうし、あっても測定する技術が無かったであろう。
. .
材料を加熱処理すること無く自然発酵させる葡萄酒はアルコール濃度が14%(重量濃度)になると発酵を停止する。従って、この葡萄酒は文献の正確な氷点データによる推定計算値−6.6°Cの固有の氷点を持つ。これを純葡萄酒と呼ぶことにする。この純葡萄酒もファーレンハイトの住む地域では冬には凍る。当時は、分析技術も確立されておらず、アルコール濃度の測定は出来なかったが、純葡萄酒に同量の水を加えれば純葡萄酒濃度50%、即ち、ほぼ7%のアルコール水溶液ができる。このようにして数点の溶液を作り、氷点を測り、純葡萄酒濃度と氷点の関係をグラフに描くと二次曲線で近似出来ることを発見した。材料を加熱処理して酵母を加えて醗酵させる酒類では14%より高いアルコール濃度は得られるが、其は氷点測定値を二次曲線に当てはめると純葡萄酒濃度100%を少し上まわる程度である。ウイスキー等の蒸留酒は冷凍技術の無い当時、凍らすことは出来ず、アルコール濃度は知り得なかった。従って、純葡萄酒の2倍、即ち、アルコール濃度28%の溶液を凍らす温度になることはあり得ないと彼は考えた。そこで、二次曲線を延長して純葡萄酒濃度200%、即ち、アルコール濃度28%の水溶液の氷点を推定した結果、水の氷点より32°低い値を得たのである。
| Table 5.1 アルコール・水溶液の氷点 | ||||
|---|---|---|---|---|
| 濃度 | 氷点 | Δ | Δ2 | ..q.. |
| 0% | 0˚ | 0 | ||
| 5% | −2.0˚ | −2.0˚ | 1 | |
| 10% | −4.5˚ | −2.5˚ | −0.5˚ | 2 |
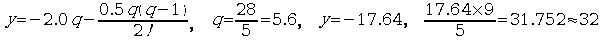
. . ファーレンハイトは今日では常識的となっている実験式という手法を最初に用いた人物であり、当時の物理学者達の多くはこの実験式という手法を知らなかったのではないだろうか。そして、1736年に彼が没した6年後の1742年にセルシウスは摂氏温度を制定したが、この時、既に華氏温度が広く普及しており、摂氏温度に目を向ける者はあまりいなかった。そこでセルシウスは華氏温度が非科学的であると強調するためにいわゆる誹謗中傷を行った。ファーレンハイトが用いた葡萄酒の色から彼は血を用いたとか、上記のファーレンハイトのデータの意味を理解できず、36を人間の体温と推定して、最初、それを12等分したが目盛が荒すぎるので96等分にしたとかの話を作り上げた。36を人間の体温とする推定はセルシウスが摂氏温度を制定した後でなければありえない。又、寒剤を用いて水の氷点より32°F低い温度を達成したと言うのも作られた話である。それらが今日にまで伝わり、華氏温度制定の経緯として百科事典にも載せられている。この温度達成については今日まで達成した者はいない。いるなら使用した寒剤の種類や分量に関する正確なデータを明記できる筈であるがそのような文献は存在しない。Table 5.1に示した程度の温度なら寒剤により達成することは可能であろう。
. . ファーレンハイトは水の氷点より32°F低い温度を達成したのではなく、Table 5.1に示した程度の氷点下の温度を寒剤により得て、アルコール水溶液の濃度と氷点の関係を求める実験を行い、水の氷点より32°F低い氷点を持つアルコール水溶液の存在を確信したのである。確かに、実験式を実験温度範囲を越えて適用することは危険である。危険であるとは否定すべきということではないし、非科学的ということでもない。否定するためには実験式に当てはまらないデータの存在を実証しなければならない。当時の物理学者は誰一人それを行っていない。今日では、水の氷点より32°F低い氷点を持つアルコール水溶液が存在し、その重量濃度が約28%であることが分かっており、装置と技術を持つものなら誰でも再現確認できる。誹謗中傷に類する説をいつまでも百科事典等に載せておくのは適当でない。ファーレンハイトの名誉回復のためにも、華氏温度の定義は「水の氷点と沸点の間を180等分した目盛を1°Fとし、水の氷点より32°F低い氷点を持つアルコール水溶液(重量濃度約28%)の氷点を0°Fとする温度」と改めるのが妥当である。
6. 1時間及び1度は何故60分か、1分は何故60秒か
. .
古代エジプト人はやがて心臓の鼓動に興味を持つが、これを1時間の単位で数えたのでは3600以上を数えなければならず、大変だった。そこで1時間を更に短い単位で区切ることを考えたが、このとき彼等は完全な周期は1440、その2分の1の720、4分の1の360と言う数値で表わされなければならないと考えた。第2節で述べた単位Adayを用いれば、4年は1440Aday、2年は720Aday、1年は360Adayである。又、60日は1440時間、30日は720時間、15日は360時間である。ここに、完全な周期1440時間の60分の1が又完全な周期24時間(1日)と言う関係が見出される。従って、24時間は1440分、即ち、1時間は60分となる。1440分の1/60、即ち、24分が1440秒になるから1分は60秒となる。
. .
この関係は1440時間の4分の1である360時間についても成立する。上記の数値の関係を全て4分の1にすればよい。360時間の1/60、即ち、6時間が完全な周期360分であるから1時間は60分であり、360分の1/60、即ち、6分が完全な周期360秒であるから1分は60秒となる。この関係は完全な周期である1回転の角度360°についても成立すると考えるから、角度1°は60分、1分は60秒となる。これが時間と角度で分と秒と言う同じ単位が使われる理由であり、且、其が60進法となる理由である。
7. 古代エジプト人の使用したπの値
. .彼らは少数を知らないからπの値は知らない。併し、与えられた半径の円を描いたとき円周長が幾らになるかを整数計算で求める方法を知っていた。即ち、彼らはπの値を数値として表現することは出来なかったが其を使用することは出来た。彼らは中心角1°の円弧長は円周長を測る単位の長さであると考えた。これを1°Lの長さと表わす。この単位長で円周長を測定すると円の大きさに関係なく360°Lとなる。この単位長1°Lで半径を測定すると理論的には360÷2π=57.295779515°Lとなるが、少数は知らないから57°Lと無視できない余りを得る。この余りはコンパスを開いた2本の針の間の長さや棒に記した2本の線の間隔のようなアナログ量として得られるのであるが、これをアナログ量として一般的に説明文に示すのは困難であるから少数を用いて示せば0.295779515°Lとなる。以降においてもこのような意味で少数を用いる。この余りを中心角1'の円弧長1'L=1°L/60で測ると、17'Lと無視できない0.7467709'Lの長さの余りを得る。この余りを中心角1"の円弧長1"L=1'L/60で測定すると44"Lと0.806254"Lの長さの余りを得る。この余りは約1"Lであるから、円周長=360°Lの円の半径は57°17'45"Lとなる。両者を1"Lの単位で表わせば、1296000"Lの円周長の円の半径は206265"Lとなる。更に両者を15で約して1'L/4=15"Lの単位長で表わせば円周長=86400に対して半径=13751となる。従って、半径10mの円の円周長を求めるには、半径を10倍にすれば円周長も10倍になり、その半径を13751で割れば円周長も13751で割れば良いから、86400×10÷13751=62m83cmとなり、整数演算の掛算と割算で円周長を求めることが出来る。この計算は下記のπの値を使用したのと等価である。
. . この円周長と半径の関係を実測で得るには中心角1°の円弧長1°Lを精確に測定する必要がある。半径1のとき1°Lの理論値はπ÷180=0.01745329252であり、中心角1°の弦長の理論値は
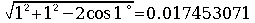 である。従って、円弧長と弦長の差を整数値で識別出来るためには
である。従って、円弧長と弦長の差を整数値で識別出来るためには. . ピラミッドの大きさから考えて半径数百メートルの円弧長1°Lを実測で求めるのは可能と考えられるが、単位長をcmとして半径をcmの精度で測定できるか疑問である。しかし、100mの半径をcmの精度で測定できたと仮定すると、この作図により得た円弧長1°Lを目盛りとした定規を作れる。この1目盛りは0.017453×
. . 半径を1°Lで測った余りを1°Lを60等分した1'Lで測る代わりに余りの60倍を1°Lで測定することが出来る。余りを60倍するには、60等分した方法でEFを余りの長さとし、最後の点Eの1つ前の点とFを結ぶ線分に平行な直線を点Oから引き、線分EFの延長線との交点を求める。交点をXとすればEXはEFの60倍3107.4cmである。これを1°Lの目盛りで測れば17'Lと余り140.39cmを得る。更に、この余りを60倍すると8423.4cmを得、これを1°Lで測ると48"Lを得る。理論的に求めた値との誤差3"Lは真の円弧長1°Lで半径を測定した余りが51.6232cmであるのに対して、弦長を1°Lとして使用したため余りは51.79cmと約2mm大きくなったことに因るものである。作図可能な円弧では中心角1°の円弧長と弦長の差を測定することは不可能であるから、この誤差を避けることは出来ない。この場合円周長1296000"Lの半径は206268"Lであるから、円周長108000に対して半径は17189となる。このときのπの値は下記の値となる。
. . 彼等は又πの値は知らなかったが円及び扇形の面積を計算することが出来た。中心角1°の弦長と円弧長1°Lとの違いは検出できないから、この扇形は底辺1°Lの二等辺三角形に同じである。故に、この扇形の面積は1°L×半径÷2となり、これを360合わせれば円の面積であるから、円の面積=円周長×半径÷2, 扇形の面積=円弧長×半径÷2である。これは上記のπを用いた計算と同じである。
| 目 次 へ | 次 へ |