1. スフィンクスは何か

. .古代エジプトのナイル川の西岸ギザの砂漠に小さな岩山があり、その東の端には巨大な岩石が塔のように突き出していてその先端の高さは20m程であった。東岸は平野の東の一段と高い所にイースタン砂漠が山脈のように南北に横たわっていた。このような地形の故に東岸では毎朝不思議な現象が見られる。朝、太陽が東の空に顔を見せる前に西岸の巨大な岩石の先端が燦々と輝き、それから太陽が顔を見せるのである。それは、巨大な岩石の先端から一条の閃光を放ち、太陽を呼び寄せたかのように見えた。この不思議な現象の見られる東岸に人々は集り住み、彼等はその巨大な岩石に太陽を制御する神が宿ると考え、西岸は死後に住む場所として住み分けた。
. . 彼等の一日はこの巨大な岩石の先端が燦々と輝いたときに始まり、次に輝いたときに終って同時に次の日が始まる。彼等の生活はこの一日の区切の他に昼間と夜と言う区切りの基で行なわれていたが、昼間は太陽が最高位置にあるとき、即ち、地面に立てた棒の影の長さが最小になるときで明確に二つに分けられることが発見され、午前と午後の区切りが生活に取り入れられる。太陽が裏の大地を照らしている裏の昼間も二つに区分でき、その時刻で表の大地の夜間は二つに区分できるから一日は四つの時刻に区分される。ここに、時刻、時間と言う概念が生まれる。彼等の時刻、時間の概念は現代人とは全く異り太陽の回転角度なのであり、時間と角度で同じ単位名が使われる理由がここにある。彼等は四つの時刻に数値を割り当てて時刻の名称として使用する。彼等の知る数値は1から始まる整数のみであり、巨大な岩石の先端が燦々と輝いたときを1、正午を2、日没を3、真夜中を4の時刻と定めた。しかし、彼等は1の時刻が一日の始まりでは可笑しいことに気が付いた。影の長さは2の時刻に対称で、太陽の高度も2の時刻に対称であるから昼間の真中は2の時刻である。夜間の真中は裏の大地の昼間の真中である4の時刻である。従って、一日の真中は2の時刻でなければならない。そこで一日を次のように定義した。「一日は4の時刻に始まり、1の時刻は日の出、2の時刻は正午、3の時刻は日没である。」
. . ここで、スフィンクスが人間に投げ掛けたと言われる「朝には4つ足、昼には2本足、夕暮には3本足で歩くものは何か」答は人間という謎々が思い出される。これは上に述べた一日の始まりと時刻の定義に一致し（1の時刻が無いが）謎々ではないであろう。文字は人間の考え、動作や自然現象を絵に描いて伝えたり記録に残したりすることに始まり、具体的な事象は記録も理解も容易であろうが、時刻、始まる、終ると言うような抽象的な事象は記録も解読も困難を伴う。これ等の記述はある約束の基に具体的な事象を記述する文字をそのまま、又は、組み合わせたり変形したりして使うがその約束は記述されず、其を使用する人達のあいだで暗黙の了解として使われるからである。今日に於も自然科学の英語の専門書を日常英語は堪能であっても専門外の人が翻訳すると分けの解らない結果になることが起こる。考古学の古文書解読の手法は日常用語の解読は出来るが、自然科学用語の解読は困難であり、多くの文書は意味の解らないことを述べているから神事や謎々の記述であるとして片付けられてしまう。古代エジプト人の自然科学はこれ等の記述の中にあるがその解明には彼等の自然科学を自然科学的に解明する必要がある。その自然科学的記述が行なわれた時点で既に神事や謎々に変っている場合も多いであろうが、彼等の自然科学が解っていれば真の意味の推測の可能な場合も多いであろう。
. . 西岸の巨大な岩石は古代エジプト人の自然科学の発展に大きな役割を演じただけで無く、自然科学には殆んど興味がない多くの人々にとっても宗教的な崇拝の対称となった。時の権力者達はその庶民の心を自分達に向けさせることが権力を万民に認めさせることになると考え、その為には自分の像をその巨岩に彫り神を人格化すれば良いと考えた。しかし、其を認めない権力者達との間で争いが起こり、ここに偶像崇拝と其を否定する宗教の争いが始まる。この争いに敗けた権力者達はエジプトを追われ、勝った権力者達はその巨岩に人間の頭部を刻んだ。その像は現在の物とは異り、イースター島のモアイ像の様なものであったと思われる。スフィンクスは人々の住む東を向き、その東方にはイースタン砂漠が山脈のように横たわっていてその高さは殆んど一様だから、太陽が何処から昇っても同じ時刻にスフィンクスの先端が輝く。しかし、イースター島の山は摺鉢状の火山であり、太陽がどの方向から昇っても同じ時刻に山頂からの光を検出する為には何体もモアイ像を並べる必要があり、それ等は人々の住む島内を向いて海岸に並べられた。彼等もスフィンクスが未だこのような素朴な像であったときにエジプトを出発した探険隊又はその子孫と考えられる。
. . エジプトでは王朝時代になって巨岩の後の岩山はライオンの胴体を刻まれ、頭部は岩石の形状を髪形にして現在の姿となった。その顔はカフラー王の顔を写しているとも言われる。スフィンクスはその後顔の一部が破壊され、偶像崇拝と其を否定する宗教の争いの痕を残す。

2. 一年は何故365日と四分の一日か

. . 古代エジプト人は西岸の巨大な岩石の先端が燦々と輝いたとき太陽の上端が東の山脈に現われた地点に顕著な目印を見つけ、そのときから太陽の回転数を数え始め、日の出地点が南下して南端に達し、北上して北端に達し、再び南下してその目印に太陽の上端が現われたとき迄の回転数を数え、一年が365日であることを知る。しかし、次の年の1日目の日の出地点は僅かに目印の北側にあり、その隔は3年、4年と増加し、5年目の1日目の日の出地点は1日分づれていて2日目の日の出地点が丁度目印と一致することを知る。これにより太陽は、4年＝365+365+365+366＝1461日を周期として回転していること、及び、太陽とシリウスが同時に東の空に現われる周期はこれと一致することを知る。ここに、一年は365日と四分の一日と決定される。彼等は整数しか知らないから1/4と言う分数は知らないが、ある物を四つに等分した内の一つの量と言う概念は存在する。ただ、其を1/4と言う数値で表わすことを知らなかった。彼等はその量が不変にして固有の量であると考えられるとき其は単位量であると考える。西洋で一般に使われるクォーターでこれを表わせば、前節で述べたように1日は4クォーターであるから、1年は1461クォーター、即ち、365日と1クォーターである。2年目の最初の1日は第2クォーターに始まり366日目の第2クォーターに終る。3年目は第3クォーターに始まり366日目の第3クォーターに終る。4年目は第4クォーターに始まり366日目の第4クォーターに終る。従って、太陽の回転数にその年の始まりのクォーターを加えるだけの簡単な操作で季節とずれることの無い暦の表示が可能になる。しかし、この方法ではある年に1日が4の時刻に始まると次の年は1日は1の時刻に始まり3年目は1日は2の時刻、即ち、正午に始まると言うことになり、前節の1日の始まりと時刻の定義に矛盾するだけでなく日常生活も不便となる。
. . 詳細な過程については後節にて述べるが、彼等は幾何学の進歩により1回転は360°であることを知る。この値は不変固有の値であるから周期現象の単位であり、周期現象は360の整数倍の値を周期として繰返していると彼等は考えた。当然、1年と言う周期も基本周期であるから360日でなければならない。考古学では太陽の回転数による360日を1年とする暦が使われた言うが、それでは季節とのずれが甚だしくて無意味である。意味が解らないから神事に使われたと言うのは妥当でない。古代エジプト人は1年を360で割った1日と言う単位があると考えたのである。これを絶対的な1日と言う意味でAdayと言う単位で表わすと、1年＝360Aday=365.25日である。このAdayを用いれば季節と暦のずれが生ずる事はないが、クォーターの使用と同様に1日の始まる時刻が4の時刻でなければならないことと矛盾する。又、今日のように1年という周期が4年毎に1日異ると言うことも認め得なかった彼等は1年は365日と定め、日の出地点の南端、北端、真中、或は太陽とシリウスが同時に東の空に現われた時より数え始め、各年の始まり等の季節行事は上記の関係式により1年=360Adayに換算して行なった。彼等は整数しか知らないから実際は4年＝1440Aday=1461日を用いて換算を行なったと考えられる。其故、現代人には解り難い日数による暦の表示が行なわれたのかもしれない。

	. .
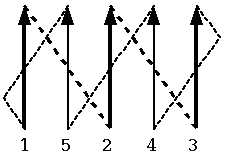Fig. 2.1

. . 彼等は1周期は360と言う数値で表わされなければならないと考えていたから、何故1年間の太陽の回転数が360回転でないのかを解明する必要があり、その為に太陽の運行図を考えた。簡単化のため大地の表を照らす走査線は東西に平行で裏を照らすとき位置を変えるとして運行図をFig. 2.1に示す。エジプトに春夏秋冬の四季をもたらすのは太陽の位置であるから、少くとも冬、春、夏を実現する為に同図の1, 2, 3の3ヵ所を走査する必要がある。北上した太陽が南下するとき春と同じ位置を走査したのでは1年に同じ場所を2度走査することになるから、このときは3本の走査線の中間を走査する必要があり、同図4, 5の2本の走査線を必要とする。結局1年に最低5本の走査線が必要である。このとき走査線3から4、及び、5から1へ移動する際は移動区間長を他の区間と同じにするために外側に1/4区間はみ出して折り返さねばならない。これ等5本の走査線の間の四つの区間に均一に走査線を加えて走査線の総数を増加する。これら5本の走査線の位置関係を維持するには、太陽が南下するときの走査線と北上するときの走査線を対にして両者が交互になるよう各区間に同数対加えなければならない。従って、各区間に1度に2本づつ計、2×4=8本づつ加える必要がある。走査線を順次加えて行くと、44回で8×44+5=357本、45回で8×45+5=365本となり、実測値と完全に一致する結果を得る。そこで、太陽はこの必要にして最少の5回転を作り出す必要から1年=360Adayより速い回転速度で回転していると彼等は考えた。
. . Fig. 2.1の運行図では365日で太陽は元の位置に戻るから1/4日のずれは生じない。実際には、地球が太陽の周りを1回転したときの自転数は整数でなく、365+約1/4回転の端数を持っているから、1年後の太陽の位置は図の走査線1の中点、即ち、正午の位置にあり、同図は太陽の1年の周期を正確に表していない。しかし、彼等は地球を知らないしその公転や自転も知らないから、このずれは太陽が南北に約45度の角度を往復する、即ち、90度回転するのに1/4日を要するからであると考えた。現代人は東西の回転速度と南北の回転速度のベクトル合成速度で太陽は回転しているから太陽がFig. 2.1に示す1の点に現われた時から2の点に現われる迄の実測時間は1から2への南北の移動時間を含んでいることを知っている。しかし、古代エジプト人はベクトル合成と言う概念を知らないから、太陽が1の点に現われた時から2の点に現われる迄の実測時間は単に1回転に要する時間であり、1から2への南北の移動には別に時間が必要と考えた。そして1年＝365日+1/4日と言う観測値との一致からこの考えは疑う余地の無いものであった。

. .

. . 4年で完全な周期となる運行図は必要な最低走査線の数を5+5+5+6=21本とした運行図で示すことが出来る。Fig. 2.1では1本の走査線を飛越し走査しているが、4年間の運行図では更に2年目、3年目、4年目の北上するときの走査線と南下するときの走査線の対の合計本数1+2+2+2=7本を飛越し走査しなければならない。その最初の1年間の運航図はFig. 2.2(a)に示すようになり、2年目の最初の走査線は1年目の最初の走査線より2区間手前にある。1区間の走査に要する時間は1/8日であるから5本の走査線では1年に1/4日足りない。4年間の日の出の位置はFig. 2.2(b)に示され、20本目の走査が終了したときこの不足分は丁度1日になるので21本目の走査線の終了したとき次の走査線は最初の走査線に戻り、21本の走査線で完全な周期となる。
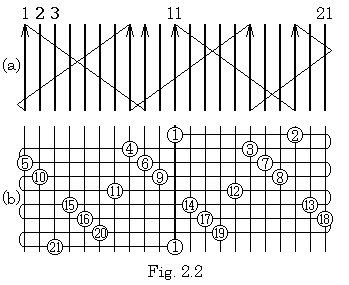. . これら21本の走査線の位置関係を崩すこと無く、間の20の区間に均一に走査線を加えるためには、太陽が北上するときの走査線と南下するときの走査線を対にして各区間に同数対加えなければならない。従って、1回に2×20=40本ずつ加える必要がある。走査線の総本数は35回で40×35+21=1400+21本、36回で40×36+21=1440+21本となり、太陽の4年間の回転数と完全に一致する。又、1461本の走査線の上にFig. 2.2(b)のように日の出位置を7本置きに順にマークして行けば日の出位置を示す曲線をプロットでき、太陽は全ての走査線を4年間に一度だけ走査し、1462本目の走査線は最初の走査線に戻ることを確認できる。
. . 太陽は4年＝1461日を周期として回転している理由は解明されたが、この周期は360日の整数倍でない。其故、太陽は更に長周期の360日の整数倍の周期で回転していると彼等は考えた。その周期は当然に1年＝360Adayの整数倍でなければならない。この長周期を求めようと彼等は下記に示す計算を行なった。その結果、太陽は1440年の長周期で回転していることを知る。即ち、1440×360Aday=1461×360日である。
. . ４年=1440Aday=1440+20+1日
. . 18×４年=18×1440Aday=18×1440+18×20+18日
. . 20×18×４年=20×18×1440Aday=20×18×1440+20×18×20+20×18日
. . これ等の計算式には考古学に於て暦の計算や表示に使われたと言われる様々な情報が含まれている。1440年、1440日、720日、20日、18日、20進法等である。そこで其れ等の記述が暦の計算や表示であるのか疑問が生じる。季節とずれない暦は4年の周期を持っているから1440年もの暦の計算や表示は全く必要がない。厳密には、現代の計算では約100年に1日の補正が必要であるが古代エジプト人がこのとき其れを知っていたとすれば上記の計算は正しくなく、長周期は1440年よりもっと長くなる。上記の計算は太陽の回転周期は360と言う数値の整数倍でなければならないと言う彼等の基本的な考えを仮定し、季節の周期とは関係なく行なったものである。この計算は僅か3行で示されているが、古代エジプト人は計算をこのような数式で表わすことを知らないし、掛算と言う算法も知らない。掛算に相当する計算は加算を繰り返して行なえるが、その加算法も現代のように各桁毎の加算と桁上と言う簡単な操作で何桁でも何個のデータでも簡単に加算を可能とする算法が確立されていたかどうか疑問である。おそらく、単純に数え上げるか、ケースバイケースで加算と桁上の正当性を証明的に文章で説明しながら行なったのではないだろうか。このような仮定では上記の計算は何十ページにもおよぶ計算書となる。その抽象的な記述は日常語を暗黙の約束の基に借りて使用する自然科学用語で記述されているが、考古学は其を日常用語としか解釈しないから暦と関係ありそうな数字との関連で暦に関する記述と解釈したのではないだろうか。1年が365日と1/4日の周期を持つことの説明も自然科学用語が解明できない状態では歴の表示と誤解されるであろう。

3. 一日は何故24時間か

. . 一日は4つの時刻に分けられることを知った古代エジプト人はやがて、その1つの時刻間の角度を一角に持ち4辺の等しい四角形を描くとその対角線は1つの時刻間を2等分し、その角度は不変固有の角度であることを知る。更に、4つの時刻で構成できる全ての角度をその不変固有の角度を1として整数で表わすことが出来る。従って、その角度は角度の単位量であり、1日は8つの時刻に分けられることを知る。即ち、1日は8の時刻に始まり、2の時刻は日の出、4の時刻は正午、6の時刻は日没である。この時代には彼等は太陽の回転角度である時間と幾何学的な角度は同じ単位を用いていた。1の時刻の角度とは8の時刻と1の時刻の間の角度の大きさであり、任意の時刻、或は時刻間、及び、任意の回転角度を測る単位の角度である。従って、1回転の角度は8の時刻の角度である。
. . 幾何学的には、直角を正四角形の対角線で2等分する方法、任意の角度を4辺の等しい平行四辺形の対角線で2等分する方法、任意の2点から等距離の点を求めるのに各々の点を中心に描いた半径の等しい円弧の交点を求める方法、これを用いて任意の角度を2等分する方法、合同や相似の概念等は確立されていた。彼等は、上記の1の時刻間は更に分割出来るから其を整数で表わすことの出来る単位量が存在するであろうと考えた。そして一本の線分の長さを半径とし、線分の両端を各々の中心とする円弧の交点と線分の両端を結んで出来る正三角形の3つの内角が等しく、不変固有の角度であることを知る。この角度は単位量ではないが、この角度と正四角形の対角線の角度の差が角度の単位となることを知る。その角度は正三角形の1つの角の1/4で、其を3つ加えると正四角形の対角線の角度になる。従って、1回転は3×8＝24に区分できる。これにより1日は24時間となる。
. . 彼等の幾何学では公理や定理は現代のように多く確定されていなかったので、現代では簡単に正しいと解ることでも克明に証明する必要があったと思われる。そこで以下に述べる一目で解る簡単な事項を公理として上に述べた彼等の考えを証明しよう。

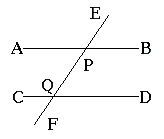Fig. 3.1	. .	1.	一回転は８の時刻の角度である。
		2.	二直線が4の時刻の角度をなすとき一直線である。
		3.	直角は2の時刻の角度である。
		4.	Fig. 3.1の様に直線ABとEFが交叉するとき相対する角は等しい、即ち、∠APF=∠EPB, ∠APE=∠FPB である。
		5.	Fig. 3.1の様に平行直線ABとCDに直線EFが交叉するとき、∠EPB=∠PQDである。

. .Fig. 3.2に示すように、正四角形OAEDの内部に描いた正三角形OACの一辺OCと正四角形の対角線OEのなす角が1の時刻の角度、即ち、∠EOAを3等分することを以下の手順で証明する。

	. .
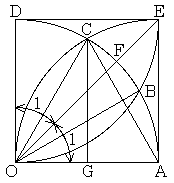Fig. 3.2

［正三角形の3つの内角は等しい］
. . 点CはOAの半径で点Oを中心に描いた円弧と点Aを中心に描いた円弧の交点であるからOC=AC=OAである。その頂角∠OCAの角度をαとする。点AはOCの半径で点Oを中心に描いた円弧と点Cを中心に描いた円弧の交点であるから頂角∠OACはαである。点OはACの半径で点Aを中心に描いた円弧と点Cを中心に描いた円弧の交点であるから頂角∠AOCはαである。 ［証明終］

［∠COEは∠EOAを3等分する］
. . 点CよりODに平行な直線CGを引くと、