3.1 Poly-processing of analyzing the construction of equations.
. . The substituting equation and binomial equation also can be poly-processed by the poly-processor, which process data by same working rule with a fixed connection of many processors which have same structure and same function. The substituting equation x=a may be binomial equation, supposing the equal sign as binomial operator denoting substitution. The elements "a" and "x" constructing binomial equation are decided to be a vector and a variable whose value is a vector. If they have only one element, they are usual numerical value or variable. However, the distinction is not done if it is not needed and they are described as the constant a and the variable x. The fundamental structure of the system analyzing equations by poly-processing is what three processors are connected as binary tree shown in Fig. 3.1(a). Every processor has three I/O ports named port 0, port 1 and port 2. Port 0 is used as root, and port 1 and 2 are used as branches to which port 0 of other processors are connected. In figure, the left branch is decided as port 1 if port number is not specified. When the elements "x, +, a" are set to the inner state of each processor as Fig. 3.1(a), it is not capable to allot them to each processor by program because the processors of this system have no address. Every processor decides its inner state by comparing the input of port 0 to its inner state.
. . When the binary tree in Fig. 3.1(a) is given the order carrying out calculation, it outputs the calculated result to port 0 by simple working rule that every processor outputs the inner state if it is numeric or outputs the result from operating the numeric value of port 1 by the numeric value of port 2 if the inner state is operator. In the case that the equation is expressed in polynomial, the inner state of every processor must be set so that the processor at the root can also output correct result by the method that all the processors carry out this working rule. When the binomial equation x+a is inputted to port 0 of the first processor as a line of letters, the first processor sets the first input "x" to the inner state, outputs the inner state to port 1 by next input "+", sets the input to the inner state and outputs the last input "a" to port 2. The processors connected to port 1 and 2 of the first processor set the input of port 0 to each inner state. The result constructs the binary tree in Fig. 3.1(a). These processing must decide the priority for setting input to the inner state so that the operator is prior to the variable and constant, and every processor needs the working rule that if the input of port 0 is prior to the inner state it outputs the inner state to port 1 and sets the input to the inner state and that if it is not so it transfers the input to port 2.
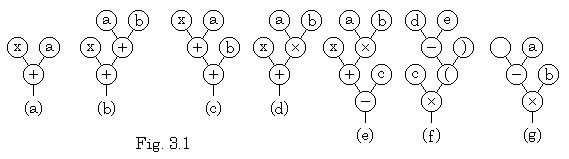
. . The equation x+a×b must construct the binary tree in Fig. 3.1(d). For the purpose, the priority for the operator to be set to the inner state must be decided that the operator "+" is prior to the operator "×". By this rule, the operator "×" inputted to the binary tree in Fig. 3.1(a) is transferred to port 2, the processor connected to port 2 sets "×" to the inner state after it outputted the inner state "a" to port 1 and the last data "b" is transferred to port 2 twice. The result becomes the binary tree in Fig. 3.1(d). The operator "−" has the same priority as the operator "+" and the operator "÷" has the same priority as the operator "×". In the latter case, the input of port 0 must be given priority when it has the same priority as the inner state for constructing the correct binary tree.
. . The equation x+a×b−c must construct the binary tree in Fig. 3.1(e). For the purpose, the first processor outputs the inner state "+" to port 1 because the operator "−" has the same priority as "+", when the first processor receives the operator "−" from port 0 after the binary tree in Fig. 3.1(d) has been constructed. Next, the first processor requires the processor at port 2 to return the inner state. The requirement is transferred to all processors connected to port 2 and the processor whose inner state is "a" or "b" outputs it to port 0. The processor whose inner state is "×" outputs the input of port 1, the inner state and the input of port 2 to port 0 in described order. The first processor sets the input "−" to the inner state after it has transferred the input "a×b" of port 2 and transfers next input "c" of port 0 to port 2. The result becomes the binary tree in Fig. 3.1(e).
. . In case when parentheses are written in equation, the binary tree whose proper processors set each parenthesis to the inner state must be constructed. In the poly-processing system, it is an important processing that the binary tree outputs the inner states by restoring to the inputted original equation together with parentheses. The equation c×(a+b) is what expresses two calculation x=a+b and c×x in one equation. The Polish notation of x=a+b is expressed in the order of "=, x, a+b", supposing a+b is the added value and it also may be expressed in the order of "=, a+b, x". The notation (a+b) denotes this Polish notation. Accordingly, the parenthesis "(" is binomial operator and the parenthesis ")" is the temporary variable, which is substituted the result of a+b and has no name. When a part of equation denotes the calculated result such Polish notation as this is used. For example, the notation of integral
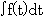denotes the integrated result by setting the integrand f(t) between the integral operate 
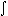and the integrating variable dt. The function f(t) is also Polish notation whose "f(" is the operator calculating the value of specified function for t and whose ")" is the temporary variable substituted the calculated value. The array used in programming is a function whose value is the value of element designated by argument. The name of array with "(" is the operator searching the specified array for the element designated by argument and the parenthesis ")" is the temporary variable substituted the searched value.. . The equation x=a+b must construct the binary tree in Fig. 3.1(b) except the inner state of the first processor is changed to "=". Accordingly, the operator "=" has priority to the operators "+", "−" in order to be set to the inner state when it is inputted from port 0. The parenthesis "(" is the operator corresponding to the operator "=" but the priority is lower than the operators "×", "÷" and the operator ")" has the same priority as variable. However, these operators have the function creating the special priority. The equation c×(d−e) must construct the binary tree in Fig. 3.1(f) because it is supposed that the inputted equation can be outputted by restoring it by use of the rule that every processor outputs the inputs of port 1, the inner state and the inputs of port 2 in order. Accordingly, the inputs (d−e) must be transformed to port 2 of the processor whose inner state is "×". However, the priority of the operator "×" is lower than the operator "−", so the priority must be changed. The change is carried out by the special priority rule that the inner state of the processor which has transferred the parenthesis "(" to port 2 or has set it to the inner state obtains the highest priority. This special priority is set double if the parenthesis "(" is inputted twice and the special priority is removed by the parenthesis ")" inputted from port 0 one by one. The processor whose inner state is the parenthesis "(" transfers all the inputs of port 0 to port 1 while it has the special priority. When all the special priority has removed by the input ")" of port 0, its priority becomes original priority and it transfers the input ")" to port 2. These parentheses "(" and ")" are pair. The function "f(" and the integral operator "
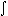" have the same priority and creation of the special priority as the parenthesis "(". The integrating variable dt removes the special priority in the same way as the parenthesis ")".. . The equation −a×b must construct the binary tree in Fig. 3.1(g). The monomial −a may be considered as the Polish notation, whose operand "0" is omitted from "−0a" which is the Polish notation of 0−a. When Polish notation is used in a polynomial equation, it is distinguished from binomial notation by continuity of two operators as "×(d−" or "=−a×" or by beginning with an operator as "−a×". If the operator "−" is used in such way, it is the monomial operator and it is differentiated from the binomial operator "−" by appending it a special flag when it is set to the inner state. The binary tree which has not the inner state "x" in Fig. 3.1(a) and changes the inner state "+" to "−" is constructed by the monomial −a inputted to the first processor. The processor receives the operator "×" from port 0 next and outputs the inner state "−" to port 1 by the special rule that if the operator "−" is monomial operator the operators "×" and "÷" are set to the inner state prior to the monomial operator and the processor sets "×" to the inner state after it has transferred "a" received from port 2 to which it demanded to return data. Next input "b" is transferred to port 2 and the binary tree in Fig. 3.1(g) is constructed.
. . BASIC program carries out the calculation of x=1+x=1 as x=1+(x=1) and the second "=" is comparison operator. The binary tree is constructed as Fig. 3.2(a). For the purpose, the first processor whose inner state is "=" transfers the second input "=" of port 0 to port 2, appending the flag denoting the comparison operator. The comparison operator is set to the inner state inferior to the four basic operators but when it has been set to the inner state it has the priority equal to the substituting operator. It is requisite for constructing correct binary tree in case of such comparison equation as x=a+b. However, it is simple as expression to parenthesize the comparison equation. In the case, the comparison operator may have the same priority to the substituting operator and the processor whose inner state is "(" may transform "=" from port 0 to port 1, appending the flag denoting the comparison operator. Accordingly, the comparison equation should be parenthesized.
. .
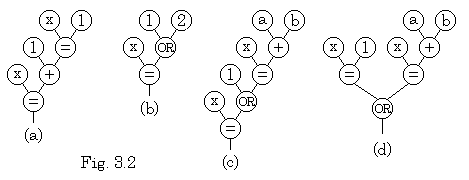
. . In this way, checking various combination of operators and operands in simple expression, the order of priority by which the input of port 0 is set to the inner state and the working rule needed to convert the expression to the binary tree are obtained.
| . .[The order of priority by which the input of port 0 is set to the inner state.] | |
|---|---|
| 1. | The fundamental priority is the order of "=", XOR, OR, AND, NOT, Relational operator, "+" | "−", MOD, \, "×" | "÷", power operator, monomial operator, "(" | "f(", variable | constant | ")" and if the order is same the latter input is prior to the former input. |
| 2. | The operator "=" which is latter input or which exists in parentheses is relational operator and is discriminated from the substituting operator by adding flag in binary tree. |
| 3. | When the operator "+" or "−" is used as monomial operator it is discriminated from the binomial operator by adding flag in binary tree. |
| 4. | The logical expression parenthesizes the operands when they are expressions. |
| . .[The working rule transforming an equation to the binary tree.] | |
|---|---|
| 1. | If the inner state is null the processor sets the input of port 0 to the inner state. |
| 2. | If the input of port 0 is prior to the inner state, the processor outputs the inner state to port 1, sets the input of port 0 to the inner state and if the inner state which was outputted to port 1 is an operator it requests for the processor at port 2 to return the inner state and transfers all the input of port 2 to port 1. |
| 3. | When the input of port 0 is the request returning the inner state the processor carries out the working rule recovering the equation from binary tree and returns to this working rule. |
| 4. | When the input "(" or "f(" of port 0 is transferred to port 1 or 2, or is set to the inner state, the inner state of the processor gets the special priority prior to all the input of port 0. The processor stacks the flag having the special priority. It takes the flag off stack one by one when it transfers the input ")" of port 0 to port 1 or 2. |
| 5. | If the inner state is prior to the input of port 0, the processor transfers the input to port 2, except that the inner state is "(" or "f(" and has the special priority. In the exception, the processor transfers the input of port 0 to port 1 except ")" and transfers the input ")" to port 2 if the special priority is single but to port 1 if it is multiple. |
| 6. | When the inner state is "+" or "−" and transfers the input of port 0 to port 2, if the processor didn't transfer anything to port 1 the processor appends the flag denoting the sign or the monomial operator to the inner state. |
| . .[The working rule recovering the equation from binary tree.] | |
|---|---|
| 1. | If the inner state is not any operator the processor outputs the inner state to port 0 and sets null to the inner state. |
| 2. | If the inner state is "(" or "f(", the processor transfers the request for port 1 and 2 to return the inner state, transfers the inner state, all the inputs of port 1 and the input of port 2 to port 0 in order and sets null to the inner state. |
| 3. | If the inner state is the monomial operator, the processor transfers the request for only port 2 to return the inner state, transfers the inner state and all the inputs of port 2 to port 0 in order and sets null to the inner state. |
| 4. | If the inner state is other operator, the processor transfers the request for port 1 and 2 to return the inner state, transfers all the input of port 1, the inner state and all the input of port 2 to port 0 in order and sets null to the inner state. |
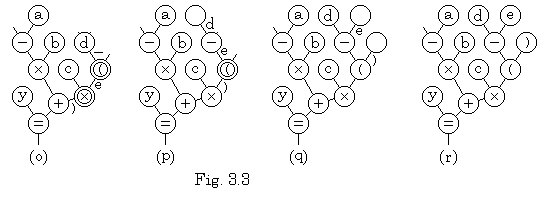
. . When the equation y=−a×b+c×(d−e) is inputted to the poly-processor constructing the binary tree, the inner state of every processor is changed as shown in Fig. 3.3. The symbols appended to the branches between processors denote the data inputted from port 0 or outputted to port 1 or 2. The processors drawn by double circles denote the special priority that the inner states is prior to all the inputs of port 0. The processing constructing this binary tree spends the total hours from the time when "y" was inputted to the first processor in Fig. 3.3(a) to the time when the last data ")" constructing the equation is inputted to it in Fig. 3.3(m) and is set to the inner state of the most right processor in Fig. 3.3(r), transferred to port 2 of serial processors. Other processors carry out their processing parallel to above processing.
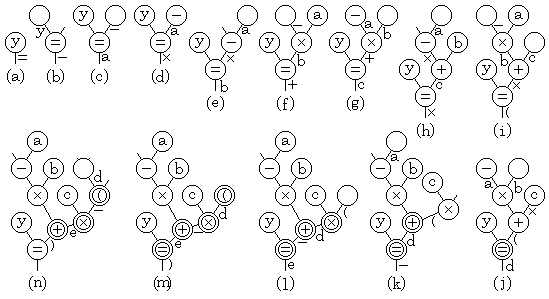
Return to CONTENTS