2.1 The poly-processing for addition and subtraction of vectors.
. . The addition and subtraction of vectors are the calculation of every element, so the parallel processing can be carried out by assigning every element to individual processor. It requires the data bus with the amount of data bits multiplied by the number of processors in order to give the value of assigned element to individual processor at the same time. Accordingly, it is not possible to use a number of processors because of the limit of hardware. The problem is solved by putting all the processors on common data bus whose bits are the bits of data and by giving the elements of vector sequentially as the order y0, Δy0, Δ2y0, ………. The first processor has the right to receive the data and gives the second processor the right when it has received y0. The second processor gives the third processor the right when it has received Δy0. In this way all the elements have been received and when the symbol denoting the end of elements has been received, the last processor loses the right and the first processor acquires the right. The processor which received two elements in the same way starts to carry out the adding or subtracting of the two elements. The transfer of data can be carried out in the time to read memory and the time lag is smaller than the time required by the floating point calculation, so all the processors finish calculating assigned element in the time when the last processor finishes calculating assigned element. It is a parallel processing practically. In case of adding and subtracting, the elements of vector may be given as the sets of x0 and y0, Δx0 and Δy0 and so on.
. . Changing the connection of processors by data bus to the connection by input/output port, the data bus can be used only for local ROM/RAM. The connection uses two input/output ports numbered as port 0 and port 1, and port 0 of every processor is connected to port 1 of former processor. By the connection all the processors do not need to be synchronized and to transfer the right to receive the data. Every processor gets the first data on port 0 by watching or by interrupt and transfers the other data to port 1. The processor which received the end symbol of vector elements starts to receive the element of next vector and to carry out the operation when it has got two elements. Parallel to the operation, the processor transfers the data for other processor. These working are programmed in the local ROM of every processor and the programs are all the same.
. . This is fundamental conception of the author's poly-processing in hardware and firmware. The poly-processor is constructed as follows generally.
| 1. | All the processors have the same hardware and software or firmware. |
| 2. | The hardware of every processor consists of Controlling unit, ALU, ROM, RAM and a few input/output ports. |
| 3. | Every processor is connected with each other in similar structure by connecting its port 0 to a port of former processor except of port 0 and only the processor at the head carry out input/output from outside. |
| 4. | The processors in the neighborhood may be connected in a group by using two I/O port, adding above main connection. |
| 5. | Every processor can store an inner state in RAM and stack it if necessary. |
| 6. | Every processor compares the data from I/O port 0 with its inner state and decides whether to store it as inner state or to output it to the port of what number. In the case of storing it as inner state, the processor decides whether to stack its inner state or to output it to the port of what number and carrying out the operation by these decision. |
| 7. | For request of data from I/O port 0, every processor outputs its inner state or the result which is operated by its inner state, requesting the data to other I/O port. |
. . The software stored in ROM of every processor is the program of the working of processor which carries out the work described in above term 5, 6, 7 and not the algorism by which a given problem is solved in usual programming. It is the fundamental work which is included in the algorism. BASIC describes the addition of vectors stored in array x, y as follows, where Δk−1x0, Δk−1y0 denote numerical values.
| 10 FOR K=1 TO 10:X(K)=Δk−1x0:NEXT:FOR K=1 TO 10:Y(K)=Δk−1y0:NEXT 20 FOR K=1 TO 10:Z(K)=X(K)+Y(K):NEXT |
In case of the author's poly-processor carrying out this work, the value K denotes the position of processor. Line 10 denotes to give the K-th processor the value of K-th element and Line 20 denotes that the K-th processor sets the result of addition of two elements to its inner state. Accordingly, in order to begin carrying out the operation when a processor has got two data, the K-th processor carries out the work for the K value of BASIC program changed as the second FOR statement of LINE 10 is deleted and Y(K)=Δk−1y0 is inserted into FOR statement of LINE 20. However, this system does not use the K value because it is equivalent to designating the address of processor. The data are inputted to the processor at head in order from left to right of Eq. (2.1).
 ____(2.1)
____(2.1)| . .[The working rule adding two vectors.] | |
|---|---|
| 1. | If the input of port 0 is "(", the processor sets it in the inner state. |
| 2. | In the case that the input of port 0 is a numeric value, if the inner state is "(" the processor stacks it, outputs the copy to port 1 and sets the input in the inner state. If the inner state is "," the processor stacks it and sets the input in the inner state. |
| 3. | If the inner state is a numeric value the processor outputs all the input of port 0 to port 1. |
| 4. | In the case that the input of port 0 is "," or ")", if the inner state is "(" the processor outputs it to port 1 and sets the input in the inner state. |
| 5. | If the inner state is ")" the processor ignores all the input of port 0 except "(". |
| 6. | If the input of port 0 is "+" the processor outputs it to port 1, loads the inner state to the accumulator of ALU and pops the inner state stacked. |
| 7. | The processor which has got the element of the second vector again by the items 1 to 5, starts adding two elements parallel to the transfer of other data to port 1. |
| 8. | The processor which has complete adding sets the result to the inner state. |
| 9. | When the processor receives the request of result from port 0, if the inner state is not ")" it outputs the request to port 1 and outputs the stacked inner state, the inner state of adding result, the input of port 1 to port 0 in described order. |
| 10. | The processor which has transfer ")" completes this processing. |
. . When the data in Eq. (2.1) are inputted to the processor at head in order from left to right, the processor sets "(" to its inner state by the working rule 1. Inputted x0, it stacks "(", transfers the copy to port 1 and sets x0 to the inner state. After this, it carries out the working rule 3. The second processor carries out the working rule 1, 4, 2, 3 by the order, receiving "("","Δx0 and it stacks "," and sets Δx0 to its inner state. In the same way, the 10-th processor stacks "," and sets Δ9x0 to its inner state, receiving "("","Δ9x0. The 11-th processor sets ")" by the working rule 4, receiving "("")" and carries out the working rule 5. The first processor had transferred ")" before 10 steps and started carrying out the working rule 6, 7, 8 by the input "+" and it sets the added result z0=x0+y0 of the first elements to its inner state. If "+" is inputted again after transfer of the end symbol ")" of elements of the vector Y, it carries out the working rule 6, 7, 8 again. If the input is the request of the result, because of the working rule 9, it outputs the stacked "(" and the inner state z0 to port 0 and transfers "," and Δz0 which are transferred to port 1 from the second processor. After it has transferred "," and Δ9z0 in the same way, it transfers ")" outputted by the 11-th processor and the adding process finishes.
. . Changing "+" of the data (2.1) to "−", the subtraction of vector is carried out. If any processor has a breakdown, the trouble is repaired by changing it for another processor or by bypassing it, because the function of processor is all the same and the processors have no address. This is the same repair as brain. Adding processors at the tail, it is possible to increase the dimension of vector and the precision of calculation increases because the increase of dimension is equivalent to increasing the degree of approximation of function. This corresponds to increasing the ability for brain to think. This system is similar structure when the data are not inputted. However, it becomes non-similar structure when the data are inputted, because every processor carries out a different item of the working rule and has a different inner state. This is similar to the brain, which becomes only protein by death.
. .
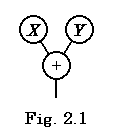 The application program using this poly-processing calculation system may describe the addition of vectors as X+Y or x+y, denoting the vectors as x and y. Accordingly, hardware even becomes ultra-parallel processing it does not need the parallelizing compiler. This equation is expressed in the binary tree constructed by the inner states of processors as Fig. 2.1. When every processor carries out the processing by the inner state, the processor whose inner state is X or Y gets the vector value and gives it to the processor whose inner state is "+". The processor whose inner state is "+" adds the two vector values. In the case, it gives the data (2.1) to above poly-processing calculation system, which is connected to the I/O port except of the I/O ports constructing binary tree. In case of complex equation, the binary tree needs many processors whose inner state are the four operation and the processors must have each poly-processing calculation system mentioned above. The above poly-processing calculation system is not very high level in parallel, so it is possible to ease the burden of hardware by that ROM of every processor has a program such as is shown above in BASIC. However, this section describes the detail of the construction as hardware, because it gives an important idea to the poly-processing of knowledge information in later section.
The application program using this poly-processing calculation system may describe the addition of vectors as X+Y or x+y, denoting the vectors as x and y. Accordingly, hardware even becomes ultra-parallel processing it does not need the parallelizing compiler. This equation is expressed in the binary tree constructed by the inner states of processors as Fig. 2.1. When every processor carries out the processing by the inner state, the processor whose inner state is X or Y gets the vector value and gives it to the processor whose inner state is "+". The processor whose inner state is "+" adds the two vector values. In the case, it gives the data (2.1) to above poly-processing calculation system, which is connected to the I/O port except of the I/O ports constructing binary tree. In case of complex equation, the binary tree needs many processors whose inner state are the four operation and the processors must have each poly-processing calculation system mentioned above. The above poly-processing calculation system is not very high level in parallel, so it is possible to ease the burden of hardware by that ROM of every processor has a program such as is shown above in BASIC. However, this section describes the detail of the construction as hardware, because it gives an important idea to the poly-processing of knowledge information in later section.
2.2 Transform of function to vector and inverse transform.
. .
In usual, when the numerical calculation treats a function it treats the values of function at equidistant points but this operational calculus treats the vector whose elements are the successive differences of the values of function. Accordingly, it is required to transform the values of function to the vector. Denoting the transform operator by "v", the data inputted to the poly-processing calculation system is expressed in Eq. (2.2), which corresponds to Eq. (2.1) without the vector X. The application program using this transform describes it as v(y(t)) and the poly-processing analyzer constructs the binary tree which changes X of Fig. 2.1 for null, Y for the function y(t) and "+" for the transform operator "v". The processor whose inner state is y(t) gets the values of function of Eq. (2.2) and the processor whose inner state is the transform operator "v" receives them and transforms them into the vector, transferring the data in Eq. (2.2) to the poly-processing calculation system.
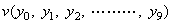 _____(2.2)
_____(2.2)
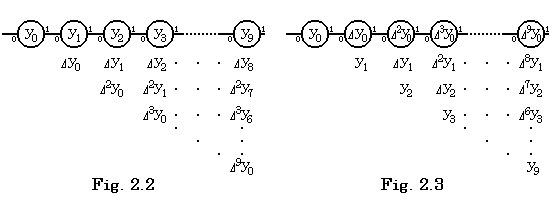
In the same way, every processor subtracts the inner state of the preceding processor from the inner state of itself. The K value denotes the position of processor and the J value denotes the head processor from which to the last processor carry out the subtraction. Accordingly, this system does not use these values. It is possible to carry out this calculation by that every processor transfers the inner state to the following processor.
. . When the head processor receives ")", which is the last datum of Eq. (2.2), from port 0, the processor transfers it and the copy of the inner state y0 to port 1 sequentially. The second processor transfers ")" received from port 0 and the copy of the inner state y1 to port 1 sequentially and the processor changes the inner state to Δy0=y1−y0 by use of y0 received from port 0 and outputs the copy of new inner state to port 1. The third processor transfers ")" received from port 0 and the copy of the inner state y2 to port 1 sequentially, changes the inner state to Δy1=y2−y1 by use of y1 received from port 0, outputs the copy to port 1, changes the inner state to Δ2y0=Δy1−Δy0 by use of Δy0 received from port 0 and outputs the copy to port 1. In the same way, the K-th processor sets Δk−1y0 to the inner state. The time spent on this calculation is the addition of the time spent on transferring ")" to the 10-th processor and the time which the 10-th processor spends on 9 times subtractions. The other processors carry out its calculation parallel to this. The processing of every processor is carried out by the same program based on the working rule mentioned bellow. The program has no description directing where to carry out parallel with other processors. However, the parallel processing is carried out.
| . .[The working rule transforming the function to the vector.] | |
|---|---|
| 1. | Every processor transfers the input "v" of port 0 to port 1 and sets one of the values of function to the inner state by the working rule adding two vectors from 1 to 5. |
| 2. | If the input of port 0 is ")" the processor transfers it and the copy of its inner state to port 1 sequentially and carried out the working described bellow. |
| 3. | If there is the value inputted from port 0, the processor subtracts the inputted value from its inner state and output the copy of new inner state to port 1. If there is no more values inputted from port 0, the processor ends the transform. |
| 4. | When the head processor receives the request outputting result, it outputs the vector value by the working rule adding two vectors 9 and 10. |
. . In usual, the numerical calculation requires the result of numerical value and not vector value. Denoting the operator transforming the vector to the values of function by "r", the data inputted to the poly-processing calculation system may be expressed in Eq. (2.3). The application program using this transform describes it as the function r(Y) and the analyzer constructs the binary tree in Fig. 2.1 whose vector X is changed to null and whose operator "+" is changed to "r". The processor whose inner state is the vector Y obtains the vector value in Eq. (2.3) and the processor whose inner state is the transform operator "r" transforms the vector to the values of function, receiving the vector value and transferring the data in Eq. (2.3) to the poly-processing calculation system.
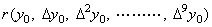 ______(2.3)
______(2.3)
2.3 The poly-processing for multiplying two vectors.
. .
The product of vectors W=XY is carried out by Theorem 1.1 in Chapter 3 Section 1.4, expanding the vector X into the matrix as shown in Eq. (2.4).
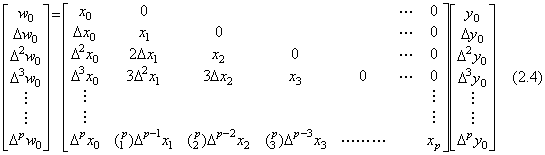
|
10 FOR J0=1 TO E2:G(J0)=X(J0):NEXT:FOR J0=1 TO E2:FOR J2=1 TO J0: __ J1=J0-J2+1:C(J2)=G(J1)*Y(J2):IF J1>1 THEN G(J1-1)=G(J1-1)+G(J1) 20 NEXT J2:IF J0>1 THEN FOR J2=2 TO J0:FOR J1=J0-J2+2 TO J0: __C(J1)=C(J1)+C(J1-1):NEXT J1,J2 30 W(J0)=C(J0):NEXT J0 |
. . In order to make the parallel processing of this multiplication possible, the array G must be two-dimensional array and must be given the values of elements removed the binomial coefficients from the matrix expressed in Eq. (2.4). The program using the two-dimensional array is described in BASIC as follows, though BASIC is not possible to process this calculation parallel.
| 10 FOR J0=1 TO E2:G(J0,1)=X(J0):NEXT:FOR J0=2 TO E2:FOR J1=2 TO J0: __ G(J0,J1)=G(J0-1,J1-1)+G(J0,J1-1):NEXT J1,J0 20 FOR J0=1 TO E2:FOR J1=1 TO J0:G(J0,J1)=G(J0,J1)*Y(J1):NEXT J1,J0 30 FOR J2=J0 TO 2:FOR J1=1 TO J2-1:G(J0,J1)=G(J0,J1)+G(J0,J1+1): __NEXT J1,J2,J0 |
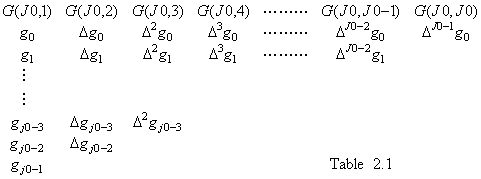
. . The application program using this system describes the product of the vectors as X×Y or x×y and the poly-processing analyzer constructs the binary tree which changes the operator "+" of Fig. 2.1 for "×". The processor whose inner state is "×" receives the vector values of X and Y and calculates the product of both by transferring the data in Eq. (2.5) to the poly-processing calculation system. The first column processors of the system set every element of the vector X to each inner state by the working rule adding two vectors from 1 to 5. They next receive the operator "×" and the other column processors are transferred it, so the processors jump to the program carrying out the product. There, at first they carry out the working rule expanding the vector to the difference table.
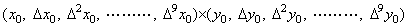 ______(2.5)
______(2.5)| . .[The working rule expanding the vector to the difference table.] | |
|---|---|
| 1. | The processor received "×" from port 0 (=Pj1) transfers it to port 1 and 3 and next it outputs the copy of the inner state to port 1, if the inner state is numeric value, but it ignores the input if the inner state is ")". |
| 2. | The processor received "×" or ")" from port 2 (=Pjk, k>1) sets it to the inner state. |
| 3. | When the input of port 0 is numeric value, if the inner state is numeric value the processor outputs the copy plus the input to port 3, if the inner state is ")" the processor outputs the copy to port 3 and if the inner state is "×" the processor waits the input from port 2. |
| 4. | When the input of port 2 is numeric value, if the inner state is "×" the processor outputs it to port 3, sets the input to the inner state, outputs the copy to port 1 and then checks the input of port 0. |
| 5. | If the input of port 0 or 2 is "(" or "," the processing jumps to the working rule multiplying the expanded matrix of vector by other vector. |
. . The inner state of every processor is set as Fig. 2.5 by working as above rule and the difference table is constructed. The row processors after the last row of the difference table set ")" to all the inner states but the description of the row is omitted. The processors stop transferring the data to on and after the row, when the table is multiplied by the elements of the vector Y. The matrix into which the vector X is expanded is the matrix whose every row consists of the row elements of the difference table multiplied by each binomial coefficient as Eq. (2.4). However, this multiplication of binomial coefficients is carried out by totaling each row as expressed in Table 2.1, when the matrix of the difference table is multiplied by the vector Y.

| . .[The working rule multiplying the expanded matrix of vector by other vector.] | |
|---|---|
| 1. | When the input of port 0 is "(" or "," if the inner state is numeric value the processor loads it to the accumulator of ALU and sets the input to the inner state, but if the inner state is ")" the processor ignores the input. |
| 2. | When the input of port 0 is numeric value, if the inner state is "(" or "," the processor outputs it to port 1, sets the input to the inner state, outputs the copy to port 1, begins multiplying the value of accumulator by the inner state but if the inner state is ")" the processor ignores the input. |
| 3. | The processor which began the multiplication transfers all the input of port 0 up to the end code ")" to port 3 after this. When the multiplication is completed the processor sets the result to the inner state and outputs the copy to port 2, but the processor Pj1, which does not use port 2 outputs no data to port 2. |
| 4. | If the inner state is "×" the processor transfers all the inputs of port 2 to port 1. When the input of port 2 is ")" the processor furthermore outputs the copy to port 2 and clears the inner state. |
| 5. | The processor which outputted the copy of the multiplied result to port 2 adds the input of port 3 to the inner state if the input is numeric value and outputs the copy of resultant inner state to port 2. If the input of port 3 is ")" the processor transfers it to port 2 and clears the inner state. |
| 6. | The processor Pj1 adds the input of port 3 to the inner state if the input is numeric value and completes the multiplication of vectors if the input of port 3 is ")". |
. . The processor which began the multiplication by the working rule 3 has a numeric value as the inner state but in the case, the processing of the input and output is different from the working rule 1 and 2 so the flag denoting the working state is required for the purpose of distinction. The state of this flag is not described except the case when the special description must be, because the flag is not what denotes the data and is the same as Ready flag and interrupt signal of I/O port. The reason is that the working state is evident by the description "The processor which began the multiplication transfers all ……… after this" as Ready state is evident by the description "When the input is numeric".
. . The processor which completed the multiplication of vectors by the working rule 6 outputs the result by the working rule adding two vectors 9, 10, receiving the requirement. The requirement of result uses "=" and appends it to the tail of the data in Eq. (2.5). It is the same in the case of adding two vectors and in transforming a function to vector.
2.4 The poly-processing for calculating the quotient of vectors.
. .
The quotient of vectors W=Y/X may be calculated by the product of vector W=X−1Y, if there exists the inverse matrix X−1 of the matrix into which the vector X is expanded. In order to avoid the calculation of the inverse matrix, multiplying the both sides by the matrix X, the quotient W can be calculated as the solution of simultaneous linear equations XW=Y. This simultaneous linear equation may be solved by changed to Eq. (2.6) and (2.7) because of the theorem 1.6 in Chapter 3 Section 1.6. If a diagonal element of the matrix X is zero the equidistant points or the domain defining the vector are not proper in calculating the elements of the vector. The element of quotient required the division by this diagonal element must be given the value previously. If it is not given the quotient of vector is not determined. The program in Chapter 4 Section 3.2 always gives zero to the diagonal element in the case so the quotient of vector is not correct generally. However, the solution using variable equidistant interval can obtain the convergent result in the domain where no diagonal element of the matrix X is zero, changing the equidistant interval because the solution does not converge. It is also possible to use the way that does not carry out the division by the diagonal element of the matrix X, if the element is zero. Accordingly, the poly-processing of the quotient of vector is described on the supposition that all the diagonal elements of the matrix X are not zero.
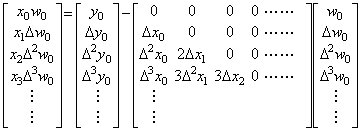 ____(2.6)
____(2.6)
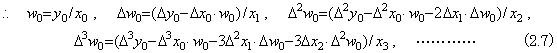
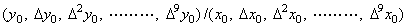 ____(2.8)
____(2.8)
| . .[The working rule expanding the divisor vector into the difference table.] | |
|---|---|
| 1. | When the input from port 0 is "/" (=Pj1), if the inner state is numeric the processor outputs the input to port 1 and port 3 and stacks the inner state. If the inner state is ")" the processor stacks the inner state. |
| 2. | The processor received "/" from port 2 (=Pjk, k>1) sets the input to the inner state. |
| 3. | If the input of port 0 is "(" the processors (=Pj1) set the elements of the divisor vector to each inner state by the working rule adding two vectors from 1 to 4 and the processor which has transferred the last ")" to port 1 outputs the copy of the numeric inner state to port 1. After the output, if the top of stack is "(" the processor (=P11) outputs it to port 1 and 3 and it goes to the working rule calculating the quotient. |
| 4. | When the input of port 0 is numeric, if the inner state is numeric the processor adds the copy to the input and outputs the result to port 3. If the inner state is ")" the processor outputs the copy to port 3. If the inner state is "/" the processor waits the input of port 2. |
| 5. | When the input of port 2 is numeric, If the inner state is "/" the processor output it to port 3, sets the input to the inner state, outputs the copy of the input to port 1 and checks the input of port 0. |
| 6. | After the rule 4 and 5, if the input of port 0 is "(" the processor transfers it to port 1 and 3, if the input of port 2 is "(" transfers it to port 3, and both processors go to the working rule calculating the quotient. But if the inner state is "/" the processor goes to the working rule calculating the quotient, reserving the transfer of "(" of port 2. |
. . The processors in the first column stack each inner state as shown in Fig. 2.6(a) by the working rule from 1 to 3 and the processors in the first and second column set the devisor or the operator to each inner state as shown in Fig. 2.6(b). The processors in the columns after the first column set the data to each inner state by the working rule 3 and 4 as shown in Fig. 2.6(c) to (d) and finish expanding the divisor to the difference table.
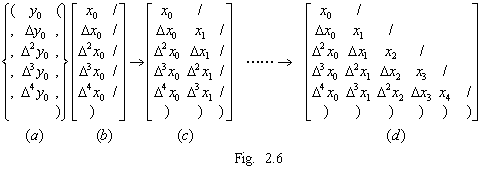
. . P22 recognizes that it is in charge of a diagonal element, because it receives "(" from port 0. Hence it stacks the inner state and sets zero to the inner state. Other processors in diagonal element process each inner state in the same way as P22 and all the inner states become Fig. 2.7(c). { } denotes the data in the stack. Pj1(j>1) output the result to port 3 after finish of calculating the product of w0 and each inner state, pop "," and Δj−1y0 of each stack and output them to port 3. P22 adds w0Δx0 received from port 2 to the inner state (=0) and calculates Δw0 by the second equation of Eq. (2.7), using Δy0 received from port 2 after ",", the resultant inner state and x1 popped from the stack. Pj2(j>2) multiply each inner state by Δw0 transferred from port 0, output the copy of each result to port 3, add the value of each port 2 to each inner state, output the result to port 3, transfer "," and Δj−1y0 to port 3.
. . P33 adds all the data of port 2 to the inner state (=0), knows the end of adding data by receiving "," and calculates Δ2w0 by the third equation of Eq. (2.7), using Δ2y0 after ",", the added resultant inner state and x2 popped from the stack. In this calculation, the totaling of the row elements multiplied by binomial coefficients is carried out by the way shown in Table 2.1 except the data is transferred inverse direction. Hence the result is obtained on the diagonal element. Here, the results are determined up to the third row as shown in Fig. 2.7(e) and in the same way the elements of quotient are obtained on the diagonal elements of Fig. 2.7(f). After this, the inner states of the diagonal processors are transferred to the first column processors. The symbole "∗" in Fig. 2.7 denotes that the inner state may be an arbitrary value. In order that all the processors can carry out this processing by use of the same program, the working rule is described as follows.
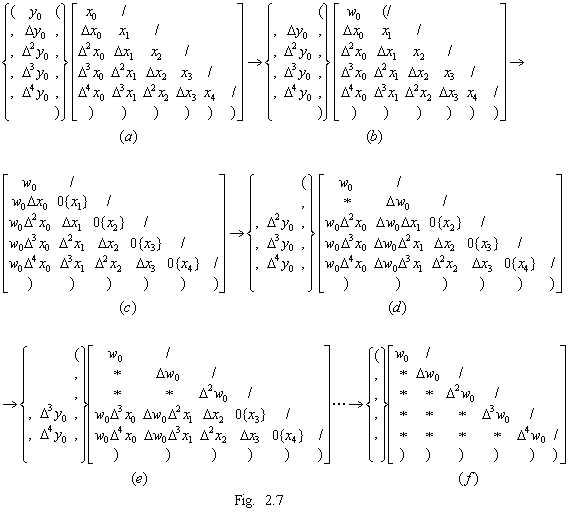
| . .[The working rule calculating the quotient from the difference table.] | |
|---|---|
| 1. | If the inner state is "/" the processor transfers the input "(" of port 2 to port 1 and finishes this processing if the input of port 2 is ",". |
| 2. | If the inner state is ")" the processor ignores (but receives) the input, which is "(" or a numeric value from port 0, and pops the data of stack to the inner state if the data of stack is ")". |
| 3. | P11, which outputted "(" of the top of stack to port 1 and 3 pops next numeric data to accumulator, divides it by the inner state, sets the result to the inner state, outputs the copy to port 1 and finishes this processing. |
| 4. | If the input of port 0 is "(" the processor (=Pjj, j>1) stacks the inner state and sets zero to the inner state. After this, the processor adds all the inputs of port 2 to the inner state if they are numeric, finishes adding if the input of port 2 is ",", outputs the input "," to port 3, subtracts the inner state from next numeric input of port 2, divides the result by the numeric value popped from the stack, sets the result to the inner state and outputs it to port 1 and 2. |
| 5. | When the input of port 0 is numeric, if the inner state is numeric the processor transfers the copy of the input to port 1, sets the product of the inner state and the input to the inner state and outputs the copy of the resultant inner state to port 3. After this, it carries out the rule 6. |
| 6. | Pj1(j>1) whose stack has "," on the top pops "," and next numeric value and outputs them to port 3. After this, the processors finishes the processing, setting the input of port 3 to the inner state. The other processors repeat that they output the copy of the resultant inner state to port 3, adding the input of port 2 to the inner state if it is numeric. If the input of port 2 is "," they finish the repeat and transfer the input "," and next numeric input of port 2 to port 3. After this it transfers the numeric input received from port 3 to port 2 and finishes the processing. |
. . If the requirement of result "=" is inputted from port 0 after the calculating system has finished the calculation of quotient, it outputs the quotient by the working rule adding two vectors 9 and 10. Although useless data remain in the inner state of processors after the output of the quotient, it causes no problem because every processor used for new calculation sets the new data to the inner state.
2.5 The poly-processing for differentiating and integrating a vector.
. .
The integral operation is notated in Eq. (2.9)(a). The notation is Polish notation because it consists of the three notations, which are the integral operator, the integrand y' (t) and the integrating variable dt in order. Polish notation is used as the notation of numerical formula in order that the computer processes the numerical formula easily. However, if it appears in the usual numerical formula it denotes the result of operation. It is evident because of the formula in which the integral notation, variables and numerical values are connected by the four operations. This poly-processing system notates the integral operation as SY' h, notating the integral operator by S and the integrating variable dt by the equidistant interval h. Expressing the notation in the binomial expression, it becomes Y' Sh so it constructs such binary tree as Fig. 2.1. The processor whose inner state is the operator "S" receives the values of the vector Y' and h, and it integrates the vector by transferring the data in Eq. (2.10) to the poly-processing calculation system.
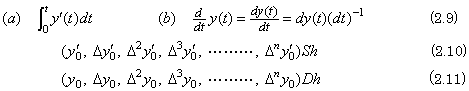
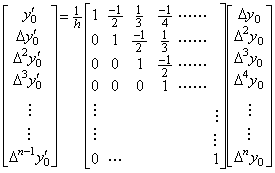 _____(2.12)
_____(2.12)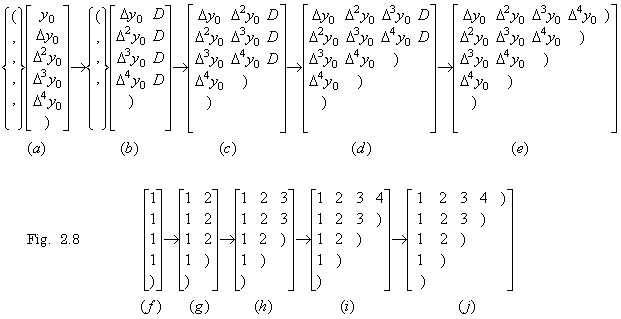
. . Parallel to above transferring of the data, the processor which has set the denominator of each element of the differential matrix to the inner state divides the element of vector in the stack by the inner state with minus if the inner state is even. When the calculation has finished the processor which is not in the first column outputs the result to port 2 and after this transfers the input of port 3 to port 2. The processor in the first column, which does not use port 2, adds all the data inputted from port 3, finishes adding if the input of port 3 is ")" and divides the added result by the input h of port 0. At finishing of these processing, the elements of the differentiated vector are set to the inner states of the processors in the first column. In order that all the processors carry out these processing by the same program, the working rule must be as follows.
| . .[The working rule differentiating the vector.] | |
|---|---|
| 1. | The processor in the first column sets the each element of the operand vector to the inner state by carrying out the working rule adding two vectors from 1 to 5 and carries out following working rule by the operator "D" inputted next except that it does not output any to port 0 if it is P11, which has "(" on the top of stack. |
| 2. | When the input of port 0 is the operator "D", if the inner state is ")" the processor finishes the processing by outputting the inner state to port 0 and if the inner state is a numeric value the processor outputs the inner state to port 0 (the inner state is cleared) after it has transferred "D" to port 1 and 3. |
| 3. | When the input of port 1 is ")", if the inner state is null the processor sets the input to the inner state, outputs the copy of the new inner state to port 0, cancels the data in the stack and finishes after canceling the input (=h) of port 0. If the inner state is a numeric value the processor transfers the input ")" to port 0 and 3. |
| 4. | When the input of port 1 is a numeric value (=an element of vector), if the inner state is null the processor sets the input to the inner state, outputs the copy of the new inner state to port 0, stacks the inner state and sets the element 1 of the differential matrix to the inner state. If it is the first input after the element of the differential matrix has been set to the inner state the processor transfers the input to port 0 and 3, outputs the copy of the inner state to port 3 and after this transfers the input of port 1 to port 0 and 3. |
| 5. | If the input of port 2 is the operator "D" the processor sets it to the inner state. |
| 6. | When the input of port 2 is a numeric value, if the inner state is "D" the processor output it to port 3 and sets the input (=an element of vector) to the inner state. If the inner state is an element of vector the processor stacks it and sets the input plus one to the inner state (=the denominator of an element of the differential matrix). If the inner state is the denominator of an element of the differential matrix the processor transfers the input (=an element of vector) to port 3, next outputs the copy of the inner state to port 3 and after this transfers the input of port 2 to port 3. |
| 7. | When the input of port 2 is ")", if the inner state is "D" the processor sets the input to the inner state, outputs the new inner state to port 2 and finishes the processing. If the inner state is a numeric value the processor transfers the input ")" to port 3. |
| 8. | Parallel to above transfer of the data, the processor which has set the denominator of an element of the differential matrix begins the calculation dividing the value in the stack by the inner state with minus if the inner state is even. |
| 9. | After the processor has finished the calculation, if it uses the port 2 it outputs the result to port 2, transfers the input of port 3 to port 2 after this and finishes the transfer if it has transferred ")" to port 2. The first column processor, which does not use port 2 sets the result to the inner state, adds the input of port 3 to the inner state, finishes adding if the input of port 3 is ")", divides the inner state by the input of port 0 (=h) with transferring the input to port 1 and finishes the processing. |
. . The integral operation is expressed in Eq. (2.13) so it can be carried out by the poly-processing, using the two-dimensional array processors. The difference between it and the differential operation is that it does not transform the operand vector to the difference of vector and that the elements of the matrix are different. The elements of the matrix can be calculated by the poly-processing by use of the inner state of Fig. 2.8(j) and Eq. (2.14) because of Theorem 4.8 in Chapter 3 Section 4. However, in order to simplify processing all the processors have the calculated values of the elements of the first row expressed in Eq. (2.15) in each ROM and the processor whose inner state is n uses the n-th value. Accordingly, the working rule integrating the vector is as follows, changing a part of the working rule differentiating the vector.
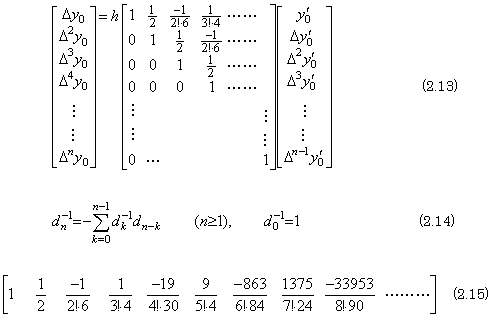
| . .[The working rule integrating the vector.] | |
|---|---|
| 1. | The processor in the first column sets the each element of the operand vector to the inner state by carrying out the working rule adding two vectors from 1 to 5 and carries out following working rule by the operator "S" inputted next except that it does not output any to port 0 if it is P11, which has "(" on the top of stack. |
| 2. | When the input of port 0 is the operator "S", if the inner state is ")" the processor finishes the processing by outputting the copy of the inner state to port 0 and by canceling the last input of port 0 (=h). If the inner state is a numeric value the processor outputs the copy of the inner state to port 0, stacks the inner state, sets the element number 1 of the integral matrix after it has transferred "S" to port 1 and 3. |
| 3. | If the input of port 1 is ")", the processor transfers the input ")" to port 0 and 3. |
| 4. | When the input of port 1 is a numeric value (=an element of vector), if it is the first input after the element number of the integral matrix has been set to the inner state the processor transfers the input to port 0 and 3, outputs the copy of the inner state to port 3 and after this the processor transfers the input to port 0 and 3. |
| 5. | If the input of port 2 is the operator "S" the processor sets it to the inner state. |
| 6. | When the input of port 2 is a numeric value, if the inner state is "S" the processor output it to port 3 and sets the input (=an element of vector) to the inner state. If the inner state is an element of vector the processor stacks it and sets the input plus one to the inner state (=an element number of the integral matrix). If the inner state is an element number of the integral matrix the processor transfers the input (=an element of vector) to port 3, next outputs the copy of the inner state to port 3 and after this transfers the input of port 2 to port 3. |
| 7. | When the input of port 2 is ")", if the inner state is "S" the processor sets the input ")" to the inner state, outputs the new inner state to port 2 and finishes the processing. If the inner state is a numeric value the processor transfers the input ")" to port 3. |
| 8. | Parallel to above transfer of the data, the processor which has set an element number of the integral matrix begins the calculation multiplying the value in the stack by the value denoted by the inner state in the element array of the integral matrix. |
| 9. | After the processor has finished the calculation, if it uses the port 2 it outputs the result to port 2, transfers the input of port 3 to port 2 after this and finishes the transfer if it has transferred ")" to port 2. The first column processor, which does not use port 2 sets the result to the inner state, adds the input of port 3 to the inner state, finishes adding if the input of port 3 is ")", multiplies the inner state by the input of port 0 (=h) with transferring the input to port 1 and finishes the processing. |
. .
After finishing the integral processing, if the input of port 0 is the request "=" of output of the result the processors in the first column output the inner state by the working rule adding two vectors from 9 to 10. This output is the difference of vector ΔY and does not include the initial value y0. When the initial value is given, in order to output the result including it the processors in the first column must carry out the addition of vector in Eq. (2.16), transferring the inner state to following processor by one. Although the working rule adding two vectors does not mention this, in the case of adding the vectors different the order of difference of vector, the position of element of both vectors must be adjust, shifting the inner state.
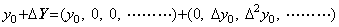 ______(2.16)
______(2.16)2.6 The poly-processing of multiplying the operators.
. . The product of a general operator and the vector except of the case that the operator is the differential operator and the integral operator, and moreover the product of any matrix X and the vector Y, that is, W=XY can be poly-processed by the poly-processing system in Fig. 2.4. It may be considered that the differential operator and the integral operator are the set of the row vectors because of the property of elements and the calculus of multiplying them by the vector. However, the author considers them as the set of the column vectors because the matrix as the expansion of a vector is also the operator and the first column is equal to the vector. The author denotes the column vector by the transposed form, parenthesizing the array of elements separated by commas, so the matrix is denoted linearly by putting the set of the vectors in brackets as Eq. (2.17). Accordingly, the product of this matrix and the vector is calculated by transferring the data in Eq. (2.18) to the poly-processing calculation system.
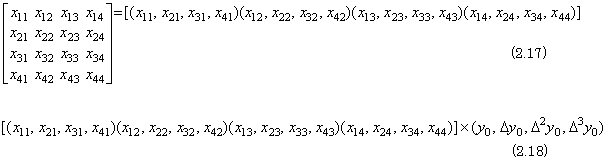
. . P11 next receives the end "]" of matrix and the operator "×" and transfers them to other processors. All the processors which receive them carry out the program which multiplies the matrix by the vector and is different from the program which is described in Section 2.3 for multiplying two vectors. The first row processors set each inner state as shown in the first row of Fig. 2.9(b) by the way that they stack each inner state by receiving the beginning "(" of elements of vector or the comma between elements and set the first numeric input of port 0 or 2 to the inner state and transfer following inputs to port 3. The processor which has set the numeric value to the inner state outputs the copy of the inner state to port 1. The processor which receives the copy from port 0 stacks the inner state, sets the input to the inner state and outputs the copy to port 1. In the result, every processor sets the inner state as Fig. 2.9(b), calculates the product of the element of matrix in the stack and the inner state and if the processor is not in the first column it outputs the result to port 2 and transfers the input of port 3 to port 2. The processor which is in the first column sets the product to the inner state and adds all the input of port 3 to the inner state. These processing set the elements of the product of matrix and vector to the inner states of the first column. The working rule for all the processors to carry out the processing by the same program is described as follows.
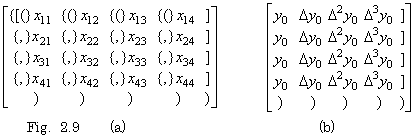
. .
| . .[The working rule inputting matrix.] | |
|---|---|
| 1. | Every processor sets the input of port 0 to the inner state if the input is the beginning "[" of matrix. The first row processors, which do not connect port 0, regard the input of port 2 as the input of port 0. The author denotes the port 0 including this port 2 by port 0(port2). |
| 2. | The processors in every column set the element in charge of each processor to the inner state by the working rule adding two vectors from 1 to 5. In the case, if the inner state is "[" and the input of port 0(port 2) is the beginning "(" of column, the processor received the input from port 0 (=P11) stacks the inner state "[" but the processor received the input from port 2 (=the first row processor except of P11) cancels the inner state "[", when it sets the input "(" to the inner state. |
| 3. | When the input of port 0(port 2) is the beginning "(" of column, if it is the input after transferred the end ")" of column to port 1(=the first row processors) the processor outputs "[" to port 3 and transfer all the inputs, which are from the input "(" to the end "]" of matrix, to port 3. |
| 4. | When the input of port 0(port 2) is the end "]" of matrix, if the inner state is the beginning "[" of matrix the processor outputs the inner state to port 1, sets the input "]" to the inner state and requires the copy of the inner state to the processor connected to port 2. If the response of port 2 is the end ")" of column the processor sets it to the inner state and if it is not so the processor outputs the copy of the inner state to port 1. |
| 5. | If the input of port 0(port 2) is the operator "×" the processor carries out the working rule multiplying the matrix by a vector. |
| . .[The working rule multiplying the matrix by a vector.] | |
|---|---|
| 1. | When the input of port 0 or port 2 is the operator "×", if the inner state is the numeric value the processor stacks it, sets the input to the inner state, and outputs the copy to port 1 and 3 if the input is of port 0 but to only port 3 if the input is of port 2. If the inner state is "]" or ")" the processor reads and cancels the input. |
| 2. | When the input of port 0(port 2) is "(", if the inner state is "×" the processor (=P11) sets the input to the inner state and cancels "[" of the stack. |
| 3. | When the input of port 0(port 2) is ",", if the inner state is "×" the processor cancels the input but if the inner state is numeric the processor transfers the input to port 3. |
| 4. | When the input of port 0(port 2) is numeric, if the inner state is "(" or "×" the processor sets the input to the inner state and outputs the copy to port 1. If the inner state is numeric the processor transfers the input to port 3. If the inner state is ")" the processor cancels the input. |
| 5. | The processor which has set the numeric value to the inner state begins the calculation multiplying the inner state by the numeric value in the stack parallel to transferring data. When the calculation has finished, the processors except of the first column processors output the result to port 2, cancel the data in the stack and transfer the input of port 3 to port 2 but the processor, which has no connection of port 2 adds the inner state all the numeric inputs of port 3 and finishes adding if the input is "]". |
| 6. | When the input of port 0 or port 2 is ")", if the inner state is numeric the processor transfers the input to port 3. If the inner state is "]" the processor transfers the input to port 1 and outputs the inner state to port 2. If the inner state is ")" the processor cancels the input. |
. . When the processor constructing the calculation system requires many times for adding than transferring data, the first column processor sets the busy flag while it is adding the input of port 3 to the inner state, then the second column processor adds two inputs of port 3 and outputs the result to port 2. The processors on and after the third column add the inputs of port 3 in the same way. By this way, the adding processing which the first column processors carry out by above working rule 5 can be made parallel processing.
. . The multiplication of two operators, that are matrices, can be calculated parallel by using the same number of the poly-processing systems in Fig. 2.4 as the column vectors which the multiplier has, because the multiplication becomes the multiplication of the multiplicand matrix and every column vector of the multiplier, dividing the multiplier into column vectors. In the case, the poly-processing systems in Fig. 2.4 are multi-layered in three dimensional array by the way that every processor prepares the I/O ports of port 4 and port 5 and that the processor which is at the same position in each layer connects its port 4 to the port 5 of the forward processor and connects its port 5 to the port 4 of the backward processor. The processors in the first layer does not connect the port 4 anywhere so they can recognize that they are in the first layer and they can carry out the processing of data by using the recognition, if necessary. The author may express a processor in the three dimensional system as P ijk if it is necessary in expression. The value i denotes the layer, the value j denotes the row in the layer and the value k denotes the column in the layer.
. . The data inputted to this calculating system are expressed in Eq. (2.19), where the data of the matrix Y follows the multiplying operator "×" in similar form to the matrix X by changing the vector Y of Eq. (2.18) to the matrix Y. When the processor in the first column of the first row of the first layer receives this data, the data are processed up to the multiplying operator "×" by the working rule inputting matrix mentioned above and set to the stack and inner state of the processors of the first layer. When the matrix X is multiplied by the first column vector of the matrix Y, it is necessary slightly to modify the working rule multiplying the matrix by a vector in order to deal the beginning "[" of matrix before the beginning "(" of the first column and to deal the beginning "(" of next column after the end ")" of the first column.
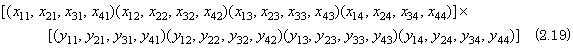
. . The processors in the first layer transfer the beginning "[" of matrix so that every processor receives it once and the processor received it outputs the copy of the element of matrix X in the stack to port 5. The outputs are received from port 4 by the processors in the second layer and they construct the matrix X which is multiplied by the second column of the matrix Y. The processor P111 receives the beginning "(" of the first column and the processors in the first layer calculate the product of the matrix X and the first column of the matrix Y by the working rule multiplying the matrix by a vector mentioned above. However, P111 does not cancel "[" in the stack by the working rule 2, because it is needed for outputting the result of product of two matrix. P111 receives the beginning "(" of the second column after it has transferred the end ")" of the first column to port 3, so it outputs "×" and "[" to port 5 and transfers the beginning "(" and all the data inputted from port 0 to port 5. The processor P211 at the top of the second layer deals the data of port 4 as the data of port 0, and the processors in the second layer calculate the product of the matrix X and the second column of the matrix Y as same way as the processors in the first layer. The processors on and after the third layer calculate the product of the matrix X and each column of the matrix Y as the same way. As the result, the product of two matrices is obtained as the inner states of the processors in the first columns of all layers. The working rule of every processor is described as follows.
| . .[The working rule multiplying two matrices] | |
|---|---|
| 1. | The processors in the first layer input the multiplicand matrix by the working rule inputting matrix from 1 to 4 and carry out the working rule mentioned below. |
| 2. | The processors (=on and after the second layer), whose port 4 are connected to former layer set the input of port 4 to the inner state and if next input of port 4 is numeric the processor stacks the inner state and sets the input to the inner state. The processor (=P i11, i>1) whose input of port 4 is "×" treats the input of port 4 as the input of port 0 on and after "×". The port is described as port 0(port 4). |
| 3. | When the input of port 0(port 4) or port 2 is the multiplying "×", the processor whose inner state is numeric stacks the inner state, sets the input to the inner state and outputs the copy of the input "×" to port 1 and port 3 if the input is of port 0(port 4) but outputs the copy to port 3 if the input is of port 2. The processor whose inner state is "]" has nothing to do and the processor whose inner state is ")" does not stack the inner state and transfers the input "×" to port 3. |
| 4. | When the input of port 0(port 4) or port 2 is the beginning "[" of matrix, the processor whose inner state is "×" outputs the copies of "(" and numeric value or "," and numeric value in stack to port 5, and transfers the input "[" to port 1 and port 3 if the input is of port 0(port 4) but transfers the input to port 3 if the input is of port 2. The processor whose inner state is "]" or ")" outputs the copy of the inner state to port 5 and transfers the input "[" to port 3. |
| 5. | When the input of port 0(port 4) is "(", if it is next input of ")" the processor outputs "×" and "[" to port 5 and transfers the input of port 0(port 4) to port 5 on and after the input "(". When it is not next input of ")", the processor set the input to the inner state if the inner state is "×" and cancels "[" of stack if it did not transfer "[". |
| 6. | When the input of port 0(port 2)(port 4) is ",", the processor only receives the input if the inner state is "×" but transfers the input to port 3 if the inner state is numeric. |
| 7. | When the input of port 0(port 2)(port 4) is numeric, the processor whose inner state is "(" or "×" sets the input to the inner state and outputs the copy of the input to port 1. The processor whose inner state is numeric transfers the input to port 3. The processor whose inner state is ")" only receives the input. |
| 8. | The processor which has set numeric value to the inner state begins the calculation multiplying the inner state by the value of the stack parallel to the transfer of data, outputs the result to port 2, cancels the data of stack and transfers the input of port 3 to port 2. However, the processor in the first column, which has no connection of port 2 adds all the input of port 3 to the inner state, which is the result of multiplication, and finishes the adding if the input of port 3 is "]". |
| 9. | When the input of port 0(port 4) or port 2 is ")", the processor whose inner state is numeric transfers the input to port 3, the processor whose inner state is "]" transfers the input to port 1 and transfers the inner state to port 2 and the processor whose inner state is ")" only receives the input. |
| 10. | When the input of port 0(port 4) is "]", if it is next input of ")" the processor transfers the input to port 5. The processor which does not receive "×" (=the last layer) cancels the inner state and stack and transfers the input to port 1 and port 3 if it is the input of port 0(port 4) but transfers the input to port 3 if it is the input of port 2. However, if the inner state is ")" the processor does not transfer the input to port 1 and if the inner state is "]" the processor does not transfer the input to port 3. |
. . The multiplication in Eq. (2.18) is equivalent to the case that the matrix Y in Eq. (2.19) has the first column only, so it can be calculated by the above multiplication of two matrices. However, it is usually expressed in Eq. (2.18) by no use of the beginning "[" and end "]" of the matrix Y. In the case, the working rules using port 4 and port 5 are not carried out and the data are not transferred to the second layer. Accordingly, the processors in the first layer obtain the same results that are obtained by the working rule multiplying the matrix by a vector.
2.7 The poly-processing of the quotient of matrices.
. .
The quotient of vectors Y/X is the matrix A expressed in the equation Y=AX. When it is not the matrix into which a vector is expanded, it cannot be calculated by use of the vector Y and X, because it is impossible to solve the simultaneous linear equations with coefficients expressed in all unknown elements of the matrix A. It is the same as that the quotient y(t)/x(t) cannot be obtained by the functions y(t) and x(t) which are denoted by the vector Y and X when the quotient is the operator such as the differential or integral operator. The matrix A must be obtained by that the function y(t) is the integral of the function x(t) expressed in the equation of differences as introduced in Chapter 3.
. .
On the other hand, the vector X is the quotient of the vector Y by the matrix A and is expressed in X=A−1Y, so it can be obtained by the poly-processing of product of the operator and the vector, calculating the inverse matrix of A. The differential operator and the integral operator do not need the calculation of the inverse operator because they are in the relation of A and A−1. In case of usual operator A, the calculation can be poly-processed by the method of elimination as simultaneous linear equations instead of the calculation of inverse matrix. Expressing the elements of the matrix A and the vector Y in one dimensional form, A−1Y may be expressed in Eq. (2.20). This calculation is binomial calculation, defining the set of the operation "−1" obtaining inverse matrix and the multiplication "×" as the operation expressing the method of elimination. Accordingly, it can be poly-processed by the two dimensional array processors in Fig. 2.4 as the same way as the multiplication of matrix and vector in Eq. (2.18).
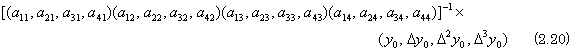
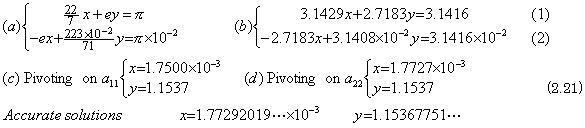
. . The processor in the first row first column outputs pivot flag to port 3 after it has transferred the end ")" of the vector Y. The processor in the first row second column receives the pivot flag from port 2 and works as pivot. In order to call the position of the pivot as the first row first column corresponding to usual calling for element of matrix, the author calls the column whose processors have the elements of the vector Y in each inner state as the column No.0. The processor in the first row first column outputs the flag denoting pivotal row to port 2 and 3, outputs the flag denoting pivotal column to port 1, next outputs the inner state a11 to these ports and sets 1 to the inner state. Other processors in the first row transfer the pivotal row flag of port 2 to port 3, output the copy of the inner state to port 1 and transfer the input a11 of port 2 to port 3 together with dividing the inner state by the input a11. That is expressed in Eq. (2.22)(c), where the processor in the column No.0 uses the input a11 of port 3.
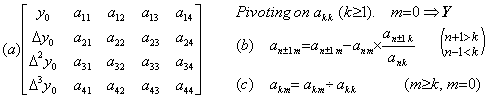 _____(2.22)
_____(2.22). . The processor in the second row second column outputs the pivotal row flag to port 2 and 3, outputs the pivotal column flag to port 0 and 1 because its port 0 is connected differently from the processor in the first row first column, outputs the inner state to these 4 ports and sets 1 to the inner state. Other processors in the second row output the inner state to port 0 too, together with the same works as the first row processors which were in the pivotal row. However, the first column processors, which were in the pivotal column before one step only transfer the input of port 3 to port 2. The processors in the second column except of the second row set zero to the inner state by the same way as the first column processors did when they were in the pivotal column and other processors carry out the calculation in Eq. (2.22)(b), where the processors in the first row carry out subtraction by using the input of port 1 and not port 0. The processor in the second row second column outputs the pivot flag to port 1 after it has set 1 to the inner state. The processor in the third row second column outputs it to port 3 and the processor in the third row third column receives it from port 2 and works as pivot.
. . When the processors in the last row and in the last column have worked as pivotal row or pivotal column in the same way, the calculation finishes and the solution is obtained in the column No.0 with the unit matrix shown by the inner state of other processors. Generally, the solution of simultaneous linear equations with n unknown consumes hours in proportion to n2 but this poly-processing system has remarkable effect that consumes hours in proportion to n. The consumption is obtained as follows. The first processor in the column No.0, whose inner state is y0 calculates Eq. (2.22)(c) when pivot is in the first row first column and carries out the calculation in Eq. (2.22)(b) n−1 times, while pivot has reached to the n-th row n-th column. This consumption of hours includes the average time in which the needful data have been transferred to the processor. In order that all the processors of this poly-processing system carried out these calculations by same program, the working rule below is needed.
| . .[The working rule for inputting simultaneous linear equations] | |
|---|---|
| 1. | Every processor inputs the matrix A by use of the working rule inputting matrix from 1 to 4 and go to the rules below by the input of the operator "−1×" denoting the method of elimination. |
| 2. | When the input of port 0 is "−1×", if the inner state is numeric the processor transfers the input to port 1 and 3, and if the inner state is ")" the processor transfers the input to port 3. |
| 3. | When the input of port 2 is "−1×", if the inner state is numeric or ")" the processor transfers the input to port 3 and if the inner state is "]" the processor does nothing except of receiving the input. |
| 4. | When the input of port 0 is the beginning "(" or separating "," of elements of vector, if the inner state is numeric the processor outputs the inner state to port 3 and sets the input to the inner state. |
| 5. | When the input of port 0 is numeric, if the inner state is "(" or "," the processor outputs the inner state to port 3 and sets the input to the inner state. After the setting, the processor transfers the input of port 0 to port 1. |
| 6. | When the input of port 0 is the end ")" of elements, if the inner state is ")" the processor transfers the input to port 3 and goes to the working rule of the method of elimination. If the inner state is numeric the processor transfers the input to port 1 and goes to the working rule of the method of elimination. In the case, the processor (=P1,0) which transferred the beginning "(" of elements of vector to port 3 by rule 5 outputs pivot flag to port 3. |
| 7. | If the input of port 2 is numeric the processor outputs the inner state to port 3 and sets the input to the inner state. If the input of port 2 is "(" or "," or ")" the processor transfers the input to port 3 and goes to the working rule of the method of elimination. |
| . .[The working rule of the method of elimination] | |
|---|---|
| 1. | If the input of port 2 is pivot flag the processor outputs pivotal row flag to port 2 and 3, outputs pivotal column flag to port 0 and 1, outputs the inner state to these ports, sets 1 to the inner state and outputs pivot flag to port 1. |
| 2. | When the input of port 2 or 3 is pivotal row flag, the processor transfers the input to port 3 if the input is of port 2 or to port 2 if the input is of port3 and outputs the copy of the inner state to port 0 and 1. The processor divides the inner state by next input of port 2 or 3 together with transforming the input to the same port as above. |
| 3. | When the input of port 0 or 1 is pivotal column flag, the processor transforms the input to port 1 if the input is of port 0 or to port 0 if the input is of port 1, outputs the copy of the inner state following the flag, divides the inner state by next input of port 0 or 1, outputs the result to port 2 and 3 and sets zero to the inner state. |
| 4. | The processor which does not receive pivotal column flag but receives numeric input from port 0 or 1, outputs the copy of the inner state to port 1 if the input is of port 0 or to port 0 if the input is of port 1, stacks the inner state and sets the input to the inner state. Next, the processor multiplies the inner state by numeric input of port 2 or 3 together with transferring the input to port 3 if the input is of port 2 or to port 2 if the input is of port 3, subtracts the product from the value in the stack and sets the result to the inner state. |
| 5. | In the case, the processor which there was in pivotal column before and set 1 or 0 to the inner state only transfers data. |
| 6. | When the input of port 0 is pivot flag, the processor transfers the input to port 3 if the inner state is numeric but returns the flag denoting end of calculation to port 0 if the inner state is ")". |
| 7. | The processor received the end flag of calculation from port 1 transfers it to port 2 and the processor received it from port 3 transfers it to port 0. In the case, the processor in the first row of the column No.0 receives the flag from port 3 but does not transfers the flag to port 0 because it has no connection of port 2 and carry out the works outputting the result vector when it receives the request of result "=" from port 0. |
| 8. | No data is outputted to the port which has no connection. (port 0 of the first row, port 2 of the column No.0) |
. .
When there exist the sets of vector Y and X which are expressed in Y=AX for a matrix A, the relation is expressed in the product of matrix Y=AX. In the case, the matrix X is the quotient of the matrix Y by the matrix A, that is, the quotient of the operators. When the determinant |A| is not zero, each column vector of the matrix X is the solution of the simultaneous linear equations in X=A−1Y, so the quotient X can be poly-processed by the three dimensional array processors whose each layer is the poly-processing system solving simultaneous linear equations mentioned above. The data inputted to this poly-processing system is expressed in Eq. (2.23) and the operation of the matrix A and each column vector Y in the matrix Y is the same as the solution of simultaneous linear equation mentioned above but the operation of the matrix A and Y needs to transfer the elements of the matrix A and the vector on and after the second column of the matrix Y to the processors in the layers on and after the second layer. The operation is carried out by the beginning "[" of the matrix Y in the same way as the product of matrices in Eq. (2.19).
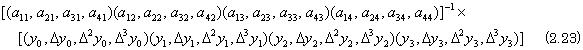
| . .[Appended working rule] | |
|---|---|
| ♦ | If the input of port 4 is numeric the processor sets it to the inner state. |
| ♦ | If the input of port 4 is the operator "−1×" the processor (=the first row of the column No.0 in the layers on and after the second layer) regards the inputs of port 4 on and after "−1×" as the inputs of port 0. |
| ♦ | If the input of port 0(port 4) or port 2 is the beginning "[" of matrix, the processor outputs the copy of the inner state to port 5 and transfers the input to port 1 and 3 if the input is of port 0(port 4) or to port 3 if the input is of port 2. |
| ♦ | When the input of port 0(port 4) is the beginning "(" of elements of vector, if it is next input of transferring the end ")" of elements of vector the processor outputs "−1×" and "[" to port 5 and transfers the input of port 0(port 4) on and after "(" to port 5. |
. .
When the vector has only one element in the poly-processing of the operational calculus mentioned above, the processing does not need to use the array processor. It can be processed by only one processor and it is usual numerical calculation. When the poly-processing system of the operational calculus is a black box, whose inner structure cannot be seen and when the structure and function of the system are supposed by only the output for inputted data, it is the most simple and easy supposition that a high-performance computer calculates the output of the data by a high degree of programming in the same way as a human does it on paper. However, it is truth that the poly-processor does the calculation by poly-processing based on simple rules. This means that the invisible world is not similar to the visible world as mentioned in Section 1.1. Not only the author's operational calculus but also all the information processing can be done by the poly-processing of the poly-processor. The good examples of the poly-processing are mentioned in the section on and after 3.2.
. .
The author thinks that the information processing in the brains is poly-processing too. Both of brain cells and body cells have same DNA. However, although body cells do synthesis of protein and cell division, brain cells do not do both of them. The author supposes that brain cells use DNA for information processing and that DNA corresponds to the tape of Turing machine or ROM of microcomputer.