5. Expanding the operational calculus into that of two variables.
5.1 The interpolation formula of two variables.
. .
When the function y(t, x) as to two variable t and x is expressed in Fig. 5.1, there exist various ways to reach the value y(tm, xn) through the equidistant points at which the line t=t0+qht intersects the line x=x0+rhx for integers q, r.
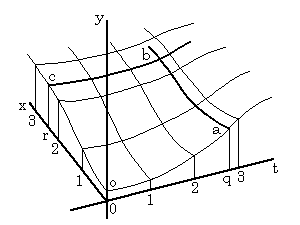
Fig. 5.1
The author adopts the two ways that the t value is incremented from t0 to tm after the x value has reached xn and that the x value is incremented from x0 to xn after the t value has reached tm. Accordingly, it is required to adopt the two sets of vectors as follows. Calculating the successive differences from the two dimensional array of the values of function at the equidistant points (tq, xr),
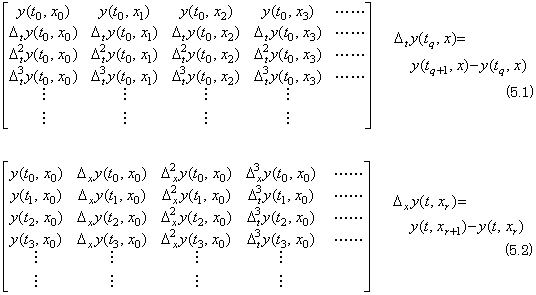 . .
The first set is the set of column vectors and the second set is the set of row vectors. If the q value is not integer and the r value is integer, the value y(tq, xr) is obtained by Newton's interpolation formula using the (r+1)th column of the set of column vectors. If the q value is integer and the r value is not integer, the value y(tq, xr) is obtained by use of the (q+1)th row of the set of row vectors. However, if the both values q and r are not integer, it is not possible to interpolate the value y(tq, xr) by use of the sets of vectors. . .
The first set is the set of column vectors and the second set is the set of row vectors. If the q value is not integer and the r value is integer, the value y(tq, xr) is obtained by Newton's interpolation formula using the (r+1)th column of the set of column vectors. If the q value is integer and the r value is not integer, the value y(tq, xr) is obtained by use of the (q+1)th row of the set of row vectors. However, if the both values q and r are not integer, it is not possible to interpolate the value y(tq, xr) by use of the sets of vectors.
. .
In order to interpolate the value y(tq, xr) by use of the function y(tq, x) denoted by a and b in Fig. 5.1, the differences Δxy(tq, x0), Δx2y(tq, x0), Δx3y(tq, x0), ……… must be interpolated instead of the values of function y(tq, x1), y(tq, x2), y(tq, x3), ………. These differences can be interpolated by use of the set of the column vectors whose elements are the successive differences of the elements on the every column of the matrix in Eq. (5.2). The set of column vectors is expressed in,
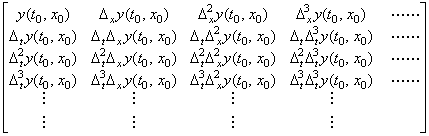 ____(5.3). .
The value y(tq, xr) may be interpolated by use of the function y(t, xr) denoted by c and b in Fig. 5.1. In the case, the differences Δty(t0, xr), Δt2y(t0, xr), Δt3y(t0, xr), ……… must be interpolated instead of the values of function y(t1, xr), y(t2, xr), y(t3, xr), ………. These differences can be interpolated by use of the set of the row vectors whose elements are the successive differences of the elements on the every row of the matrix in Eq. (5.1). The set of row vectors is expressed in, ____(5.3). .
The value y(tq, xr) may be interpolated by use of the function y(t, xr) denoted by c and b in Fig. 5.1. In the case, the differences Δty(t0, xr), Δt2y(t0, xr), Δt3y(t0, xr), ……… must be interpolated instead of the values of function y(t1, xr), y(t2, xr), y(t3, xr), ………. These differences can be interpolated by use of the set of the row vectors whose elements are the successive differences of the elements on the every row of the matrix in Eq. (5.1). The set of row vectors is expressed in,
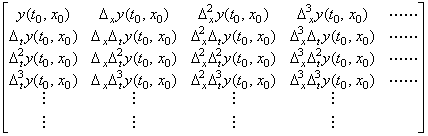 ____(5.4). .
These two sets of vectors are equivalent because these interpolate the same value as the value of function at any point (tq, xr). The first column of the matrix in Eq. (5.4) is equal to the first column of the matrix in Eq. (5.3) and the both first row are equal. The other elements of both matrices are equal to each other by the following theorem. Hence the set of row vectors is equal to the set of column vectors. ____(5.4). .
These two sets of vectors are equivalent because these interpolate the same value as the value of function at any point (tq, xr). The first column of the matrix in Eq. (5.4) is equal to the first column of the matrix in Eq. (5.3) and the both first row are equal. The other elements of both matrices are equal to each other by the following theorem. Hence the set of row vectors is equal to the set of column vectors.. .
[Theorem 5.1]. .
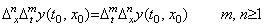 __________(5.5) __________(5.5)
[Proof]. .1) When m=n=1, the equation is satisfied because of,
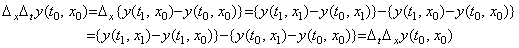 2) Supposing the equation is satisfied for some m value and some n value,
2) Supposing the equation is satisfied for some m value and some n value,
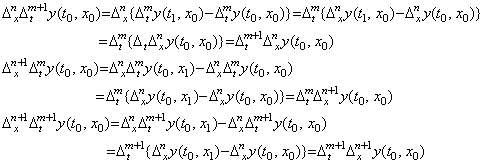
. .
The author defines these sets of vectors as the two-dimensional vector denoting the function of two variables. The expression y(t0, x0) may be expressed in y0 or y, if there is no confusion. The first column of the two-dimensional vector in Eq. (5.3) may be expressed in the vector Yt because it is the vector of the function y(t, x0) whose variable is t. The second column may be expressed in the vector ΔxYt because it is the vector of the function Δxy(t, x0)=y(t, x0+hx)−y(t, x0). The third column may be expressed in the vector Δx2Yt and so on. Accordingly, the two-dimensional vector may be expressed in,
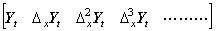 __________(5.6)
The author calls the row vector as the double vector because its elements are also vector. The first row of the two-dimensional vector in Eq. (5.4) may be expressed in the vector Yx because it is the vector of the function y(t0, x) whose variable is x. The second row may be expressed in the vector ΔtYx because it is the vector of the function Δty(t0, x)=y(t0+ht, x)−y(t0, x). In the same way, the rows on and after the third may be expressed in Δt2Yx, Δt3Yx, ………. Accordingly, the two-dimensional vector may be expressed in the double vector, which is the column vector and expressed in the transposed form as, __________(5.6)
The author calls the row vector as the double vector because its elements are also vector. The first row of the two-dimensional vector in Eq. (5.4) may be expressed in the vector Yx because it is the vector of the function y(t0, x) whose variable is x. The second row may be expressed in the vector ΔtYx because it is the vector of the function Δty(t0, x)=y(t0+ht, x)−y(t0, x). In the same way, the rows on and after the third may be expressed in Δt2Yx, Δt3Yx, ………. Accordingly, the two-dimensional vector may be expressed in the double vector, which is the column vector and expressed in the transposed form as,
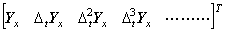 __________(5.7)
If there is no confusion, the row vector in Eq. (5.6) may be denoted by Yt and the column vector in Eq. (5.7) may be denoted by YxT. These two double vectors are equal. __________(5.7)
If there is no confusion, the row vector in Eq. (5.6) may be denoted by Yt and the column vector in Eq. (5.7) may be denoted by YxT. These two double vectors are equal.
. .
When the variables q, r are not integer as expressed in Fig. 5.1, The initial value and successive differences of the function y(tq, x) is calculated by Newton's interpolation formula with remainder as follows, using the double vector in Eq. (5.6).
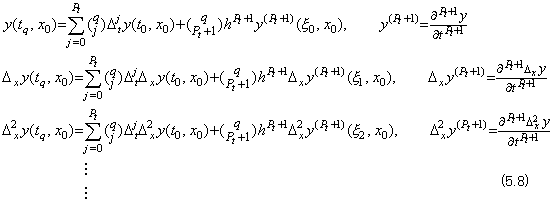 Accordingly, the value of the function y(tq, xr) is calculated by Newton's interpolation formula with remainder, using the values on the left sides of above equations.
Accordingly, the value of the function y(tq, xr) is calculated by Newton's interpolation formula with remainder, using the values on the left sides of above equations.
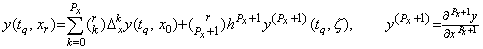 ______(5.9)
Therefore the interpolation formula of two variables with remainder is, ______(5.9)
Therefore the interpolation formula of two variables with remainder is,
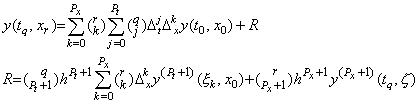 _____(5.10) _____(5.10)
5.2 Differentiation of the double vector.
. .
The operation differentiating the functions y(t, x0), y(t, x1), y(t, x2), y(t, x3), ……… are expressed in the author's operational calculus as follows, because they are the functions as to the variable t only.
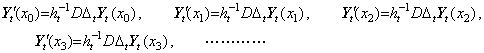 _____(5.11)
The successive differences as to x are, _____(5.11)
The successive differences as to x are,
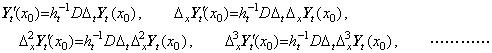 _____(5.12)
The left side vectors are the elements of the double vector of the partial derivative y' (t, x) as to the variable t. Accordingly, the equations in Eq. (5.12) is expressed in the differential operation of the double vector as, _____(5.12)
The left side vectors are the elements of the double vector of the partial derivative y' (t, x) as to the variable t. Accordingly, the equations in Eq. (5.12) is expressed in the differential operation of the double vector as,
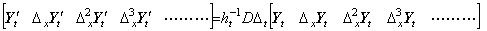 ____(5.13)
The operator ht−1DΔt denotes the partial differential operation as to the variable t and is distributed to the elements of the double vector as the scalar of usual vector operation. If there is no confusion, the partial differential operation may be expressed in the followings, denoting the double vector by the first element. ____(5.13)
The operator ht−1DΔt denotes the partial differential operation as to the variable t and is distributed to the elements of the double vector as the scalar of usual vector operation. If there is no confusion, the partial differential operation may be expressed in the followings, denoting the double vector by the first element.
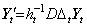 __________(5.14). .
Differentiating the functions y(t0, x), y(t1, x), y(t2, x), y(t3, x), ……… of the variable x, __________(5.14). .
Differentiating the functions y(t0, x), y(t1, x), y(t2, x), y(t3, x), ……… of the variable x,
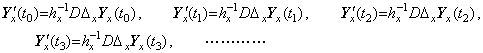 ____(5.15)
The successive differences as to t are, ____(5.15)
The successive differences as to t are,
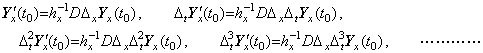 ____(5.16)
The left side vectors are the elements of the double vector of the partial derivative y' (t, x) as to the variable x. The double vector is expressed in the transposed form as Eq. (5.7). Accordingly, the equations in Eq. (5.16) is expressed in the differential operation of the double vector as, ____(5.16)
The left side vectors are the elements of the double vector of the partial derivative y' (t, x) as to the variable x. The double vector is expressed in the transposed form as Eq. (5.7). Accordingly, the equations in Eq. (5.16) is expressed in the differential operation of the double vector as,
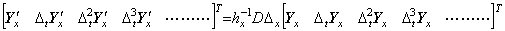 ____(5.17)
The double vectors on the both sides can be replaced by the double vector on the respective side of Eq. (5.13), because they are equal respectively. Accordingly, Eq. (5.17) may be expressed in, ____(5.17)
The double vectors on the both sides can be replaced by the double vector on the respective side of Eq. (5.13), because they are equal respectively. Accordingly, Eq. (5.17) may be expressed in,
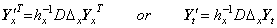 ________(5.18)
Since there is the case of ht=hx=h, it is distinguished by the subscript letter of the operator Δ whether the operation is the differential as to the variable t or the variable x. Accordingly, the partial differentiation of the double vector may be expressed in, ________(5.18)
Since there is the case of ht=hx=h, it is distinguished by the subscript letter of the operator Δ whether the operation is the differential as to the variable t or the variable x. Accordingly, the partial differentiation of the double vector may be expressed in,
 __________(5.19). .
Differentiating the partial derivatives y' (t, x0), y' (t, x1), y' (t, x2), y' (t, x3), ……… by the variable t and the partial derivatives y' (t0, x), y' (t1, x), y' (t2, x), y' (t3, x), ……… by the variable x, the second partial differential operation of the double vector is expressed in, __________(5.19). .
Differentiating the partial derivatives y' (t, x0), y' (t, x1), y' (t, x2), y' (t, x3), ……… by the variable t and the partial derivatives y' (t0, x), y' (t1, x), y' (t2, x), y' (t3, x), ……… by the variable x, the second partial differential operation of the double vector is expressed in,
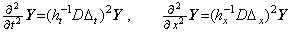 __________(5.20)
Differentiating the partial derivative ∂y(t, x)/∂t by the variable x, and differentiating the partial derivative ∂y(t, x)/∂x by the variable t, __________(5.20)
Differentiating the partial derivative ∂y(t, x)/∂t by the variable x, and differentiating the partial derivative ∂y(t, x)/∂x by the variable t,
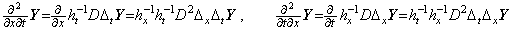 _____(5.21)
These two partial derivatives are equal because the difference operators Δt and Δx are commutative. _____(5.21)
These two partial derivatives are equal because the difference operators Δt and Δx are commutative.
5.3 The integral of the double vector.
. .
Supposing the function of two variables expressed in Fig. 5.1 is the partial derivative y' t(t, x)=∂y/∂t, the integral of the derivatives y' t(t, x0), y' t(t, x1), y' t(t, x2), y' t(t, x3), ……… are expressed in,
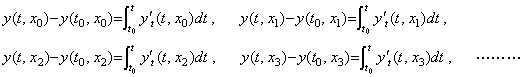 ____(5.22)
The initial values of these integrals at t=t0 are all zero and are not the results of integration. Accordingly, these integrals are expressed in the vector equations as, ____(5.22)
The initial values of these integrals at t=t0 are all zero and are not the results of integration. Accordingly, these integrals are expressed in the vector equations as,
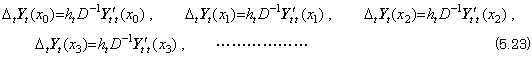 The successive differences of the equations in Eq. (5.22) as to x are expressed in the successive differences of the vector equations in Eq. (5.23) as,
The successive differences of the equations in Eq. (5.22) as to x are expressed in the successive differences of the vector equations in Eq. (5.23) as,
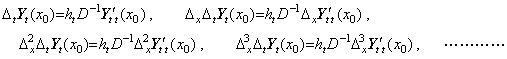 ____(5.24)
These equations are expressed in the equation of the double vectors as, ____(5.24)
These equations are expressed in the equation of the double vectors as,
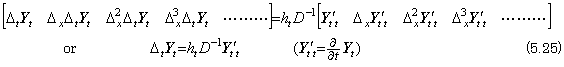 . .
Supposing the function of two variables expressed in Fig. 5.1 is the partial derivative y' x(t, x)=∂y/∂x, the integral of the derivatives y' x(t0, x), y' x(t1, x), y' x(t2, x), y' x(t3, x), ……… are expressed in, . .
Supposing the function of two variables expressed in Fig. 5.1 is the partial derivative y' x(t, x)=∂y/∂x, the integral of the derivatives y' x(t0, x), y' x(t1, x), y' x(t2, x), y' x(t3, x), ……… are expressed in,
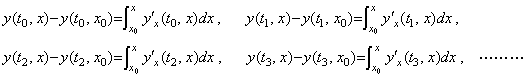 ____(5.26)
The initial values of these integrals at x=x0 are all zero and are not the results of integration. Accordingly, these integrals are expressed in the vector equations as, ____(5.26)
The initial values of these integrals at x=x0 are all zero and are not the results of integration. Accordingly, these integrals are expressed in the vector equations as,
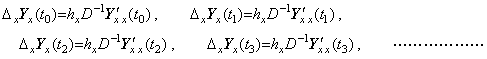 ____(5.27)
The successive differences of the equations in Eq. (5.26) as to t are expressed in the successive differences of the vector equations in Eq. (5.27) as, ____(5.27)
The successive differences of the equations in Eq. (5.26) as to t are expressed in the successive differences of the vector equations in Eq. (5.27) as,
 ____(5.28)
These equations are expressed in the equation of the double vectors as, ____(5.28)
These equations are expressed in the equation of the double vectors as,
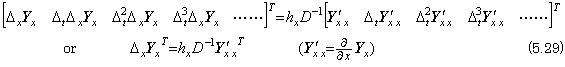 . .
The double vector in the left side of Eq. (5.25) is the submatrix which excludes the first row from the matrix in Eq. (5.3) and is expressed in the product of Δt and the matrix in Eq. (5.3), that is, the product of Δt and the double vector Yt. In the same way, the double vector in the left side of Eq. (5.29) is the submatrix which excludes the first column from the matrix in Eq. (5.4) and is expressed in the product of Δx and the matrix in Eq. (5.4), that is, the product of Δx and the double vector YxT. Because of Yt=YxT, Eq. (5.25) and Eq. (5.29) are expressed in, . .
The double vector in the left side of Eq. (5.25) is the submatrix which excludes the first row from the matrix in Eq. (5.3) and is expressed in the product of Δt and the matrix in Eq. (5.3), that is, the product of Δt and the double vector Yt. In the same way, the double vector in the left side of Eq. (5.29) is the submatrix which excludes the first column from the matrix in Eq. (5.4) and is expressed in the product of Δx and the matrix in Eq. (5.4), that is, the product of Δx and the double vector YxT. Because of Yt=YxT, Eq. (5.25) and Eq. (5.29) are expressed in,
 ______(5.30). .
When the function expressed in Fig. 5.1 is the partial derivative y"t(t, x)=∂2y/∂t2 or y"x(t, x)=∂2y/∂x2, the double integrals of the respective derivatives are expressed in the followings by the similar way. ______(5.30). .
When the function expressed in Fig. 5.1 is the partial derivative y"t(t, x)=∂2y/∂t2 or y"x(t, x)=∂2y/∂x2, the double integrals of the respective derivatives are expressed in the followings by the similar way.
 ______(5.31)
When the function expressed in Fig. 5.1 is the partial derivative y"tx(t, x)=∂2y/∂x∂t, ______(5.31)
When the function expressed in Fig. 5.1 is the partial derivative y"tx(t, x)=∂2y/∂x∂t,
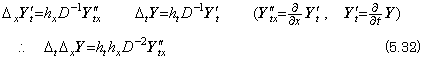
5.4 The triple vector denoting the function of three variables.
. .
The function of three variables y(t, x, z) is the function of two variables, when the variable z is equal to a constant z0. The function y(t, x, z0) is expressed in the two dimensional vector as Eq. (5.3), so it is expressed in the double vector Y(z0). In the same way, the functions y(t, x, zk) at equidistant points zk=z0+khz are expressed in the two dimensional vectors and the double vectors Y(zk). The value of the function at t=t0+qht, x=x0+rhx, z=z0+shz is interpolated as to z, after the value of the function at (t, x, z0) has been interpolated. The purpose requires that the two dimensional vector at z=zk is the k-th difference of the above two dimensional vectors as to z. The author calls the set of the two dimensional vectors satisfying the requirement the three dimensional vector. The three dimensional vector is expressed in the ordered set of the successive differences of the double vectors as,
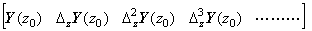 ______(5.33)
The author calls the ordered set the triple vector because its elements are the double vectors. The parentheses, z0 and the subscript letter z may be omitted, because the triple vectors which consist of the double vectors at t=t0+iht and at x=x0+jhx are equivalent to the triple vector in Eq. (5.33). The triple vector is also expressed in the first element Y if there is no confusion. ______(5.33)
The author calls the ordered set the triple vector because its elements are the double vectors. The parentheses, z0 and the subscript letter z may be omitted, because the triple vectors which consist of the double vectors at t=t0+iht and at x=x0+jhx are equivalent to the triple vector in Eq. (5.33). The triple vector is also expressed in the first element Y if there is no confusion.
. .
When the function of three variables is the partial derivative as to t, denoting it by y' t(t, x, z), the partial derivatives y' t(t, x, z0), y' t(t, x, z1), y' t(t, x, z2), y' t(t, x, z3), ……… are expressed in the double vectors which are equal to the partial derivatives of the double vectors denoting the functions y(t, x, z0), y(t, x, z1), y(t, x, z2), y(t, x, z3), ……….
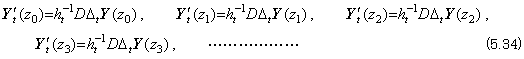 The ordered set of the successive differences as to z are expressed in,
The ordered set of the successive differences as to z are expressed in,
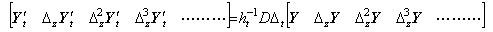 ______(5.35)
In the same way, the partial derivatives as to x and z are obtained. Denoting the triple vector by Y, they are expressed in, ______(5.35)
In the same way, the partial derivatives as to x and z are obtained. Denoting the triple vector by Y, they are expressed in,
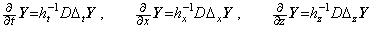 ______(5.36)
The integral operations are introduced by the inverse operation of the partial differentiation as follows. ______(5.36)
The integral operations are introduced by the inverse operation of the partial differentiation as follows.
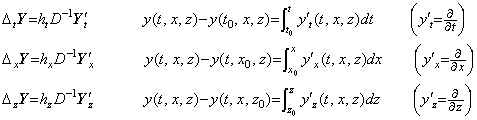 ______(5.37)
The higher order partial derivatives and the multiple integrals as the inverse operation are introduced in the same way. ______(5.37)
The higher order partial derivatives and the multiple integrals as the inverse operation are introduced in the same way.
Return to CONTENTS
|

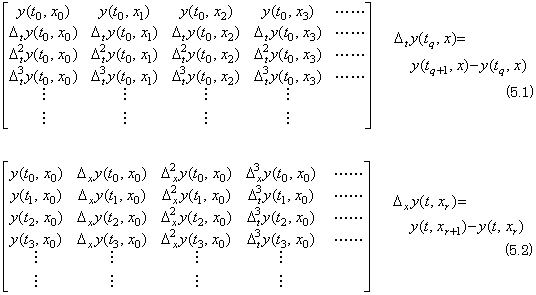
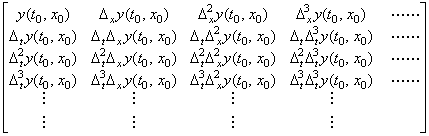 ____(5.3)
____(5.3)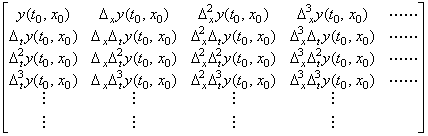 ____(5.4)
____(5.4)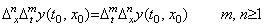 __________(5.5)
__________(5.5)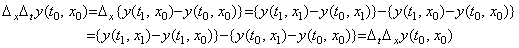
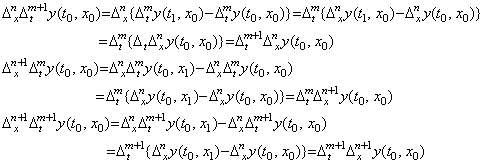
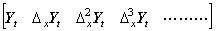 __________(5.6)
__________(5.6)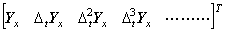 __________(5.7)
__________(5.7)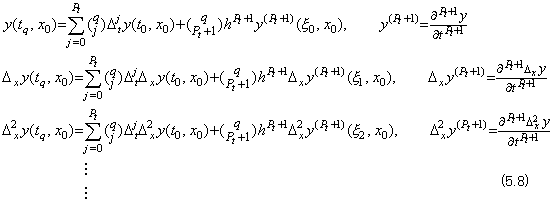
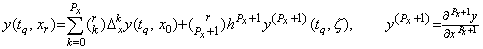 ______(5.9)
______(5.9)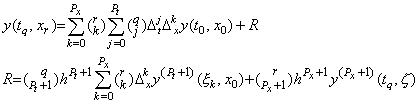 _____(5.10)
_____(5.10)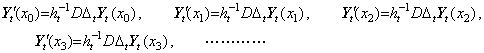 _____(5.11)
_____(5.11)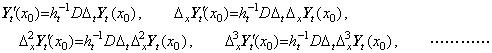 _____(5.12)
_____(5.12)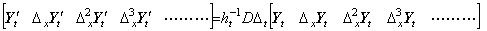 ____(5.13)
____(5.13)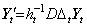 __________(5.14)
__________(5.14)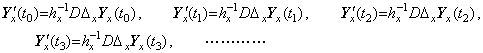 ____(5.15)
____(5.15)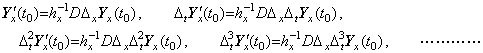 ____(5.16)
____(5.16)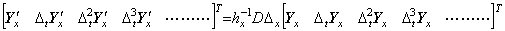 ____(5.17)
____(5.17)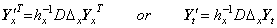 ________(5.18)
________(5.18) __________(5.19)
__________(5.19)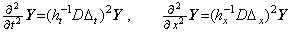 __________(5.20)
__________(5.20)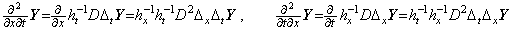 _____(5.21)
_____(5.21)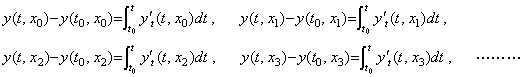 ____(5.22)
____(5.22)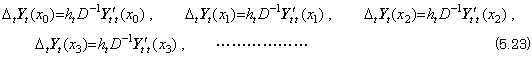
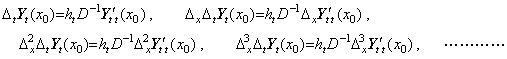 ____(5.24)
____(5.24)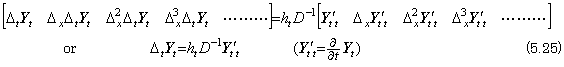
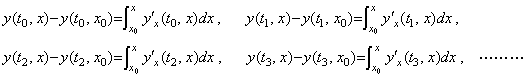 ____(5.26)
____(5.26)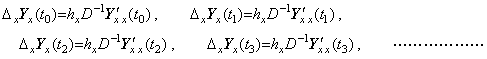 ____(5.27)
____(5.27) ____(5.28)
____(5.28)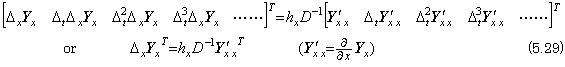
 ______(5.30)
______(5.30) ______(5.31)
______(5.31)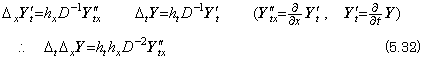
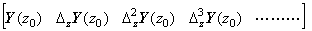 ______(5.33)
______(5.33)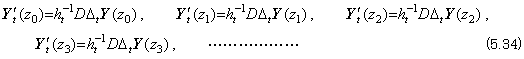
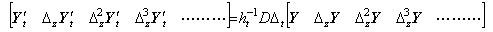 ______(5.35)
______(5.35)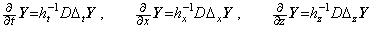 ______(5.36)
______(5.36)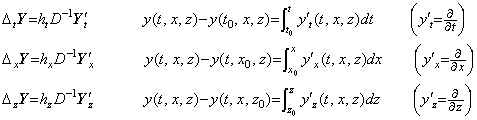 ______(5.37)
______(5.37)