4. The differential analysis and the integral synthesis.
4.1 Introducing an empirical formula by differentiation.
. .
Taylor's expansion of a function y(t) is expressed in Eq. (2.25) of Section 2.3. The last term is the remainder and it is expressed usually in the n multiple integral of the mean value y(n)(ξ) instead of the n-th derivative y(n)(t). Accordingly, Taylor's expansion in Eq. (2.25) is the solution of the differential equation y(n)=y(n)(ξ). The differential equation is equivalent to the lower order differential equation which is obtained theoretically. Differentiating the m-th order theoretical differential equation by n−m times, the n-th derivative y(n)(t) is obtained and the initial values y(m)(t0) to y(n−1)(t0) depend on the initial values y(t0) to y(m−1)(t0), which are the initial values of the theoretical differential equation. Accordingly, the n-th order differential equation has only the fundamental solutions which are the m fundamental solutions of the theoretical differential equation.
. .
The value ξ approaches to t0 by Theorem 4.17 in Chapter 3 Section 4.7 if the n value is sufficiently large. In the case, the differential equation may be approximated by y(n)=y(n)(t0) and the solution of the differential equation gives an empirical formula. Constructing the difference table from the data obtained by an experiment, the vector Y is obtained and premultiplying it by the differential operator successively, the vectors Y' , Y", ………, Y(n) are obtained. The first elements are the initial values y0, y0' , y0", ………, y0(n). These initial values are also obtained by use of Eq. (2.31) and the vector ΔY only.
. .
When the data of the swing of a pendulum are given as shown in the column yk of Table 4.1(a), the vector ΔY is obtained by the first row of the difference table constructed in the right columns of the column yk. Substituting the vector ΔY into Eq. (2.31), the values hky0(k) are obtained as shown in Table 4.1(b). These are the values of the derivative dy(t)/dq at q=0, where the relation of t and q is t=qh, h=0.25π. Accordingly, Taylor's expansion as to the variables q and t is expressed in Eq. (4.1).
|
Table 4.1 Calculating the empirical formula of the swing of a pendulum. |
|---|
| (a) | ___ | (b) |
| t/π | k | yk | Δ | Δ2 | Δ3 | Δ4 | k | hky0(k) |
0
0.25
0.5
0.75
1.0 | 0
1
2
3
4 | 00.322397
0.207880
0.067020
0 | 0.322397
-0.114517
-0.140860
-0.067020 | -0.436914
-0.026343
0.073840 | 0.410571
0.100183 | -0.310388 | 0
1
2
3
4 | 00.755308
-1.132007
0.876153
-0.310388 |
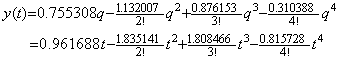 ______(4.1). .
The empirical formula gives the accurate values at the equidistant points t=kh for k=0, 1, 2, 3, 4 but the coefficients are very inaccurate comparing with the coefficients of the theoretical formula, which is expressed in, ______(4.1). .
The empirical formula gives the accurate values at the equidistant points t=kh for k=0, 1, 2, 3, 4 but the coefficients are very inaccurate comparing with the coefficients of the theoretical formula, which is expressed in,
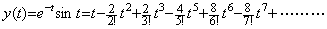 ______(4.2)
In order to improve the accuracy of the coefficients, the order of the approximated differential equation must be made higher or the equidistant interval taking the data must be made smaller. In case that the interval is h=0.05π, the accuracy of coefficients are improved as shown in Table 4.2(b). Accordingly, the correct empirical formula must be made the accuracy of the coefficients satisfied by the trial changing the interval taking the data of displacement. ______(4.2)
In order to improve the accuracy of the coefficients, the order of the approximated differential equation must be made higher or the equidistant interval taking the data must be made smaller. In case that the interval is h=0.05π, the accuracy of coefficients are improved as shown in Table 4.2(b). Accordingly, the correct empirical formula must be made the accuracy of the coefficients satisfied by the trial changing the interval taking the data of displacement.
| Table 4.2 In case of the interval h=0.05π. |
|---|
| (a) | t/π | yk | Δ | Δ2 | Δ3 | Δ4 | Δ5 |
00.05
0.10
0.15
0.20
0.25 | 00.133695
0.225707
0.283394
0.313576
0.322397 | 0.133695
0.092012
0.057687
0.030182
0.008821 | -0.041683
-0.034325
-0.027505
-0.021361 | 0.007358
0.006820
0.006144 | -0.000538
-0.000676 | -0.000138 |
|
|
| (b) | k | 1 | 2 | 3 | 4 | 5 |
| hky0(k) | 0.157096 | -0.049419 | 0.0079235 | -0.000262 | -0.000138 |
| y0(k) | 1.000104 | -2.002877 | 2.044360 | -0.430350 | -1.443044 |
. .
The empirical formula cannot be extrapolated to the outer range of experiment, even if the coefficients have sufficient accuracy. The extrapolation becomes possible, if the empirical formula can be expressed in the theoretical differential equation. It is easy to obtain the theoretical differential equation by use of the data obtained by experiment, because it requires only the initial values of lower order derivatives and they are obtained accurately.
4.2 Introducing the theoretical differential equation from the data by experiment.
. .
When a differential equation has been introduced from the data by experiment, the differential equations obtained by differentiating it any times are all equivalent. Hence, the lowest order differential equation must be obtained. It may be carried out by the trial increasing the order of differential equation successively from the first order.
. .
Supposing the differential equation is the n-th order differential equation with constant coefficients, it may be expressed in Eq. (4.3) when it is accelerated by a function f(t). If the accelerating function is the impulse function defined by the author in Chapter 2 Section 3.2, the function f(t) must be identical with zero because the impulse function is equivalent to one included with the initial value of y(n−1). If the accelerating function is the unit step function u(t), the differential equation becomes the (n+1)th order differential equation accelerated by the impulse function by differentiating.
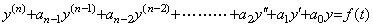 ____(4.3). .
Differentiating Eq. (4.3) n−1 times, following differential equations are obtained. ____(4.3). .
Differentiating Eq. (4.3) n−1 times, following differential equations are obtained.
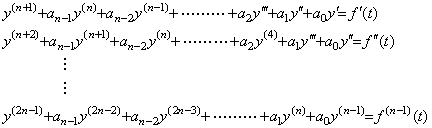 ___(4.4)
If the data are taken at equidistant points in the range from zero to t sufficiently larger than 2nh, where the h value is very small equidistant interval, they give the accurate initial values from y0 to y0(2n−1) and the values from f(0) to f(n−1)(0) as shown in previous section. Accordingly, the system of n equations substituted t=0 for the equations in Eq. (4.3) and Eq. (4.4) gives the unique solutions from a0 to an−1 and the differential equation in Eq. (4.3) is determined. ___(4.4)
If the data are taken at equidistant points in the range from zero to t sufficiently larger than 2nh, where the h value is very small equidistant interval, they give the accurate initial values from y0 to y0(2n−1) and the values from f(0) to f(n−1)(0) as shown in previous section. Accordingly, the system of n equations substituted t=0 for the equations in Eq. (4.3) and Eq. (4.4) gives the unique solutions from a0 to an−1 and the differential equation in Eq. (4.3) is determined.
. .
Differentiating the last equation of Eq. (4.4),
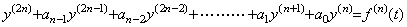 ____(4.5)
The 2n multiple integral of the derivative y(2n)(t) gives the remainder of the solution y(t) expressed in Taylor's expansion using the initial values from y0 to y0(2n−1). If Eq. (4.5) is satisfied for all the t values, the remainder is correct and the differential equation in Eq. (4.3) is what we should find out. It requires that the initial values from y0(n) to y0(2n) satisfy Eq. (4.5) substituted t=0. Accordingly, if the requirement is not satisfied, the differential equation in Eq. (4.3) is not correct and the trial of the (n+1)th order differential equation must be carried out. If the requirement is satisfied, the following theorem certifies Eq. (4.3) to be the differential equation what we should find out. ____(4.5)
The 2n multiple integral of the derivative y(2n)(t) gives the remainder of the solution y(t) expressed in Taylor's expansion using the initial values from y0 to y0(2n−1). If Eq. (4.5) is satisfied for all the t values, the remainder is correct and the differential equation in Eq. (4.3) is what we should find out. It requires that the initial values from y0(n) to y0(2n) satisfy Eq. (4.5) substituted t=0. Accordingly, if the requirement is not satisfied, the differential equation in Eq. (4.3) is not correct and the trial of the (n+1)th order differential equation must be carried out. If the requirement is satisfied, the following theorem certifies Eq. (4.3) to be the differential equation what we should find out.. .
[Theorem 4.1]. .If the initial values obtained by the experiment satisfy Eq. (4.5) at t=0, Eq. (4.5) is satisfied for all the t values.
[Proof]. .If Eq. (4.5) is not satisfied at some points except of t=0, there exists a function r(t) whose value is zero at t=0 and it is expressed in,
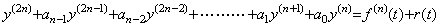 ____(4.6)
Integrating the both sides from t=0 to any t, ____(4.6)
Integrating the both sides from t=0 to any t,
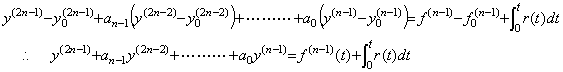 This is in contradiction to the last equation of Eq. (4.4)._________________[Q.E.D.]
This is in contradiction to the last equation of Eq. (4.4)._________________[Q.E.D.]. .
In case of the swing of the pendulum mentioned in previous section, making the interval h taking the data small sufficiently and the range [0, nh] of time large sufficiently, the correct initial values are obtained by the method mentioned in previous section as y0=0, y0' =1, y0"=−2, y0(3)=2, y0(4)=0 at t=0. By use of these initial values, the differential equation can be obtained as follows.
[1] Supposing the differential equation is y' +ay=0, the initial value y0' =1 is not satisfied.
[2] Supposing the differential equation is y"+ay' +by=0,
 Therefore the second order differential equation is what we should find out.
Therefore the second order differential equation is what we should find out.
. .
If the pendulum is set at y0=1 and released at t=0, we obtain the initial values y0' =−1, y0"=0, y0(3)=2, y0(4)=−4 at t=0 by experiment. The differential equation can be obtained as follows.
[1] Supposing the differential equation is y' +ay=0, the coefficient is a=1. However, the initial value y0"=0 does not satisfy the differential equation y"+y' =0 at t=0.
[2] Supposing the differential equation is y"+ay' +by=0,
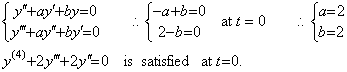 Therefore the second order differential equation is what we should find out.
Therefore the second order differential equation is what we should find out.
. .
When the initial values y0=0, y0' =0, y0"=1, y0(3)=−2, y0(4)=2, y0(5)=0, y0(6)=−4 are obtained by the data of the system accelerated by the unit step function, the differential equation can be obtained by integrating the differential equation accelerated by the impulse function.
[1] Supposing the differential equation is y' +ay=δ(t), the initial values must satisfy y' +ay=0. It is satisfied for any value a, but y"+ay' =0 does not satisfied.
[2] Supposing the differential equation is y"+ay' +by=δ(t),
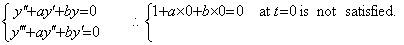 [3] Supposing the differential equation is y(3)+ay"+by' +cy=δ(t),
[3] Supposing the differential equation is y(3)+ay"+by' +cy=δ(t),
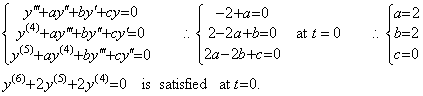 The differential equation y(3)+2y"+2y' =0 is equivalent to y(3)+2y"+2y' =δ(t) with the initial value y0"=0 instead of y0"=1 as mentioned in Chapter 2 Section 3.6. Integrating the differential equation accelerated by the impulse function from zero to any t,
The differential equation y(3)+2y"+2y' =0 is equivalent to y(3)+2y"+2y' =δ(t) with the initial value y0"=0 instead of y0"=1 as mentioned in Chapter 2 Section 3.6. Integrating the differential equation accelerated by the impulse function from zero to any t,
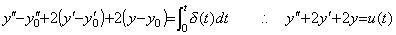 ______(4.7)
It is also obtained by integrating the differential equation y(3)+2y"+2y' =0 with the initial value y0"=1 from zero to any t as, ______(4.7)
It is also obtained by integrating the differential equation y(3)+2y"+2y' =0 with the initial value y0"=1 from zero to any t as,
 ______(4.8). .
When the accelerating function is f(t)≡1, the solution y(t) is defined at −∞<t<+∞. In the case that the accelerating function is the unit step function, the solution is the part of y(t) for t≥0, that is, y(t)u(t) and all the derivatives are y(n)(t)u(t). Accordingly, the differential equation accelerated by the unit step function may be obtained as the differential equation accelerated by the function f(t)≡1. ______(4.8). .
When the accelerating function is f(t)≡1, the solution y(t) is defined at −∞<t<+∞. In the case that the accelerating function is the unit step function, the solution is the part of y(t) for t≥0, that is, y(t)u(t) and all the derivatives are y(n)(t)u(t). Accordingly, the differential equation accelerated by the unit step function may be obtained as the differential equation accelerated by the function f(t)≡1.
[1] Supposing the differential equation is y' +ay=1, the initial values do not satisfy it.
[2] Supposing the differential equation is y"+ay' +by=1, the initial values always satisfy it for any values a, b, so it cannot be used for determining the value a, b. Differentiating it,
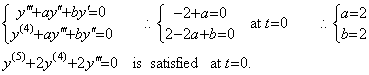 Therefore, the differential equation y"+2y' +2y=u(t) is what we should find out.
Therefore, the differential equation y"+2y' +2y=u(t) is what we should find out.
. .
In order to determine the differential equation with constant coefficients, we may use the initial values at any point or the values of y and derivatives at some points. When the swing of pendulum gives the initial values y0=0, y0' =1, y0"=−2, y0(3)=2, y0(4)=0 at t=0, it gives the values of y and derivatives at t=h as follows.
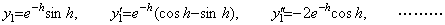 Supposing the differential equation is y"+ay' +by=0,
Supposing the differential equation is y"+ay' +by=0,
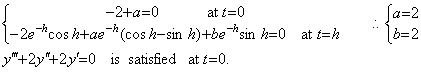 Therefore the second order differential equation is what we should find out. The third order differential equation may be checked at t=h.
Therefore the second order differential equation is what we should find out. The third order differential equation may be checked at t=h.
. .
In the case that the differential equation has variable coefficients, it is not easy to determine these because these are changed by differentiation. When the following initial values are obtained at t=0, the coefficients of differential equation cannot be determined by the system of equations at t=0.
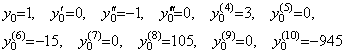 [1] Supposing the differential equation is y' +ay=0, the coefficient is a=0 but the initial value y0"=−1 does not satisfy the differential equation y"=0.
[1] Supposing the differential equation is y' +ay=0, the coefficient is a=0 but the initial value y0"=−1 does not satisfy the differential equation y"=0.
[2] Supposing the differential equation is y"+ay' +by=0,
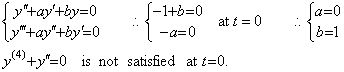 [3] Supposing the differential equation is y(3)+ay"+by' +cy=0,
[3] Supposing the differential equation is y(3)+ay"+by' +cy=0,
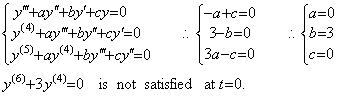 [4] Supposing the differential equation is y(4)+ay(3)+by"+cy' +dy=0,
[4] Supposing the differential equation is y(4)+ay(3)+by"+cy' +dy=0,
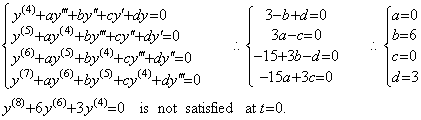 Accordingly, what we should find out is the differential equation of the higher order than the fourth order. Otherwise the coefficients are not constant.
Accordingly, what we should find out is the differential equation of the higher order than the fourth order. Otherwise the coefficients are not constant.
[1] Supposing the differential equation is y' +aty=0, the initial values satisfy it at t=0 for any constant a. Differentiating it to determine the constant,
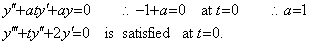 Therefore, the differential equation y' +ty=0 is what we should find out.
Therefore, the differential equation y' +ty=0 is what we should find out.
. .
When the following initial values are obtained at t=0, the differential equation whose accelerating function f(t) is identical with zero has not constant coefficients.
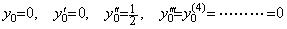 [1] Supposing the differential equation is y' +ay=0, the initial values satisfy it at t=0 for any coefficient a. Differentiating it to determine the coefficient, the initial values do not satisfy the differential equation y"+ay' =0 for all the values of a.
[1] Supposing the differential equation is y' +ay=0, the initial values satisfy it at t=0 for any coefficient a. Differentiating it to determine the coefficient, the initial values do not satisfy the differential equation y"+ay' =0 for all the values of a.
[2] Supposing the differential equation is y"+ay' +by=0, the initial values do not satisfy it for all the values of a and b.
[3] Supposing the differential equation is y(3)+ay"+by' +cy=0,
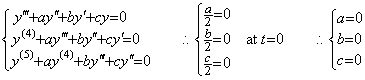 It is evident that the differential equation y(3)=0 is correct. However, it is integrable and equivalent to the second order differential equation accelerated by f(t)=1/2 as,
It is evident that the differential equation y(3)=0 is correct. However, it is integrable and equivalent to the second order differential equation accelerated by f(t)=1/2 as,
 ________(4.9). .
The second order differential equation mentioned above step [1] can be satisfied by the initial values, if the coefficient of y' is replaced by the variable coefficient a/y' . The differential equation is equal to the differential equation in Eq. (4.9). Supposing the first order differential equation has the variable coefficient a/y' , the differential equation y' +(a/y' )y=0 is satisfied by the initial values for any value a, because of ________(4.9). .
The second order differential equation mentioned above step [1] can be satisfied by the initial values, if the coefficient of y' is replaced by the variable coefficient a/y' . The differential equation is equal to the differential equation in Eq. (4.9). Supposing the first order differential equation has the variable coefficient a/y' , the differential equation y' +(a/y' )y=0 is satisfied by the initial values for any value a, because of
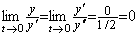 Differentiating it to determine the coefficient a,
Differentiating it to determine the coefficient a,
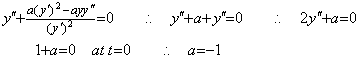 The initial values satisfy the third order differential equation 2y(3)=0. Therefore, the first order differential equation in Eq. (4.10) is what we should find out.
The initial values satisfy the third order differential equation 2y(3)=0. Therefore, the first order differential equation in Eq. (4.10) is what we should find out.
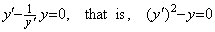 ________(4.10). .
These empirical formula expressed in differential equations can be applied to all the range from t=−∞ to t=+∞ or from t=0 to t=+∞, whereas the data is given in very small interval near to t=0. The author calls expressing the empirical formula in the differential equation as the differential analysis and solving the differential equation as the integral synthesis. He also thinks that the data processing of human is carried out by these two operations. When human sees a ball curving, he estimates the initial speeds of throwing and rotating the ball and throws a curve ball by giving the initial speeds. Accordingly, he analyzes the input data by the differential analysis and synthesizes the output by the integral synthesis. In the case of pattern recognition the data obtained by above experiments are the patterns given and the differential equation shows that the patterns except of the last two patterns fall into the category called the dumped oscillation of pendulum. The human brain can draw the locus of the swing of pendulum by integrating the differential equation. ________(4.10). .
These empirical formula expressed in differential equations can be applied to all the range from t=−∞ to t=+∞ or from t=0 to t=+∞, whereas the data is given in very small interval near to t=0. The author calls expressing the empirical formula in the differential equation as the differential analysis and solving the differential equation as the integral synthesis. He also thinks that the data processing of human is carried out by these two operations. When human sees a ball curving, he estimates the initial speeds of throwing and rotating the ball and throws a curve ball by giving the initial speeds. Accordingly, he analyzes the input data by the differential analysis and synthesizes the output by the integral synthesis. In the case of pattern recognition the data obtained by above experiments are the patterns given and the differential equation shows that the patterns except of the last two patterns fall into the category called the dumped oscillation of pendulum. The human brain can draw the locus of the swing of pendulum by integrating the differential equation.
. .
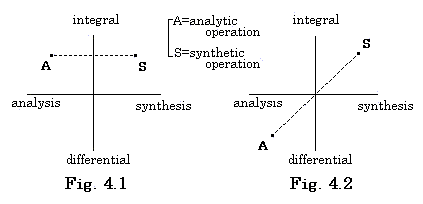
In usual, if the analysis is carried out by the integral operation called Fourier's transform, the synthesis is carried out also by the integral operation called inverse Fourier's transform. The relation of the two operations is expressed in Fig. 4.1 and the two operations are symmetric with respect to the vertical axis. The relation of the differential analysis and the integral synthesis is expressed in Fig. 4.2 and the two operations are symmetric with respect to the origin. The author calls the former as the similar operations and the latter as the symmetric operations with respect to a point. The author says that the data processing of human always is carried out by the symmetric operations with respect to a point in the case of inputting and outputting. These are mentioned in Chapter 5 as the data processing of the poly-processor.
4.3 The frequency spectrum by the differential analysis.
. .
When the output of a system is expressed in Eq. (4.11), y(t)−x(t) is the solution of the second order differential equation whose accelerating function is identical with zero as expressed in Eq. (4.13).
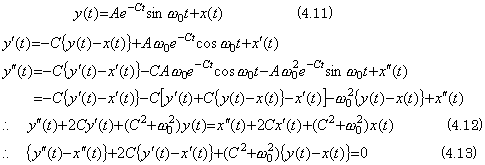 Denoting the right side of Eq. (4.12) by f(t), the function y(t) is the solution of the second order differential equation accelerated by f(t) as expressed in Eq. (4.14). The function x(t) is the particular solution of the differential equation expressed in Eq. (4.15).
Denoting the right side of Eq. (4.12) by f(t), the function y(t) is the solution of the second order differential equation accelerated by f(t) as expressed in Eq. (4.14). The function x(t) is the particular solution of the differential equation expressed in Eq. (4.15).
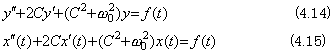 Accordingly, the particular solution x(t) is the output of the second order system for the input f(t). The first term of Eq. (4.11), that is, the complementary function denotes the characteristics of the second order system and does not denote that the input f(t) has the component of the frequency ω0, because there exists the term even if the input is the sinusoidal function of any frequency ω. The complementary function decreases in amplitude and vanishes according to the dumping ratio included in the coefficient C of the differential equation, so it is called transient response. The particular solution is the steady state output when the input is the sinusoidal function. Its amplitude and phase are given by the values B and B1 expressed in Eq. (4.16) and give the frequency response of the second order system by Fourier's transform.
Accordingly, the particular solution x(t) is the output of the second order system for the input f(t). The first term of Eq. (4.11), that is, the complementary function denotes the characteristics of the second order system and does not denote that the input f(t) has the component of the frequency ω0, because there exists the term even if the input is the sinusoidal function of any frequency ω. The complementary function decreases in amplitude and vanishes according to the dumping ratio included in the coefficient C of the differential equation, so it is called transient response. The particular solution is the steady state output when the input is the sinusoidal function. Its amplitude and phase are given by the values B and B1 expressed in Eq. (4.16) and give the frequency response of the second order system by Fourier's transform.
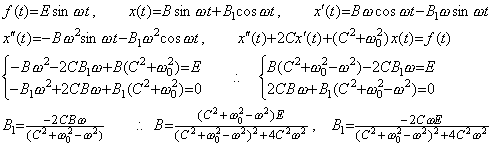 ___(4.16)
Denoting the undumped natural frequency by ωn and the dumping ratio by ζ0, the frequency response has a peak in the modulus of amplitude at the resonant frequency as expressed in Eq. (4.17), when the dumping ratio is ζ02<1/2. ___(4.16)
Denoting the undumped natural frequency by ωn and the dumping ratio by ζ0, the frequency response has a peak in the modulus of amplitude at the resonant frequency as expressed in Eq. (4.17), when the dumping ratio is ζ02<1/2.
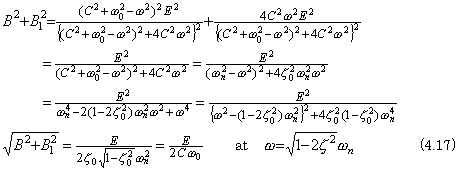 . .
When the input is any function f(t), the data of the output y(t) in Eq. (4.11) nearby t=0 give the initial values, . .
When the input is any function f(t), the data of the output y(t) in Eq. (4.11) nearby t=0 give the initial values,
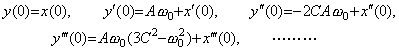 and the data of the input f(t) nearby t=0 give f(0) and f' (0). Accordingly, the coefficients of the second order differential equation are determined as follows.
and the data of the input f(t) nearby t=0 give f(0) and f' (0). Accordingly, the coefficients of the second order differential equation are determined as follows.
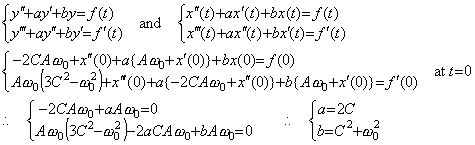 The natural frequency ω0, the undumped natural frequency ωn and the dumping ratio ζ0 are obtained from the coefficients a and b as,
The natural frequency ω0, the undumped natural frequency ωn and the dumping ratio ζ0 are obtained from the coefficients a and b as,
 . .
When the dumping ratio is sufficiently smaller than 0.7, the steady state output x(t) is nearly equal to the sinusoidal function with the resonant frequency. The amplitude and the initial values at any point t0 are obtained from the data of the output nearby t0. The initial values give the coefficients of the second order differential equation and the coefficients give the undumped natural frequency and the natural frequency in Eq. (4.18). These values give the amplitude E of the resonant component included in the input f(t) by Eq. (4.17). Accordingly, varying the resonant frequency of the second order system, the frequency spectrum of the input f(t) is obtained. . .
When the dumping ratio is sufficiently smaller than 0.7, the steady state output x(t) is nearly equal to the sinusoidal function with the resonant frequency. The amplitude and the initial values at any point t0 are obtained from the data of the output nearby t0. The initial values give the coefficients of the second order differential equation and the coefficients give the undumped natural frequency and the natural frequency in Eq. (4.18). These values give the amplitude E of the resonant component included in the input f(t) by Eq. (4.17). Accordingly, varying the resonant frequency of the second order system, the frequency spectrum of the input f(t) is obtained.
. .
This frequency spectrum is the local frequency spectrum, because it is obtained by the data nearby t0. However, it is also the frequency spectrum of the entire range of t if the input f(t) is not such a function that some functions f1(t)u(t−t1), f2(t)u(t−t2), ……… are joined or superposed, because the differential equation of the system is identical everywhere in the entire range. If the input f(t) is the joined or superposed function, the local frequency spectrum varies at the joined or superposed points. However, the local frequency spectrum between every interval [tn, tn+1] is identical with the frequency spectrum of the function fn(t). In this case, if the interval between the joined or superposed points is very small, there exists the frequency spectrum of the transient responses which occur at the edge of every interval.
. .
The input f(t) may be expressed in the general solution of a differential equation accelerated by the function identical with zero. The differential equation is obtained by the initial values f(0), f ' (0), f "(0), ……… as,
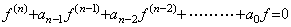 ________(4.19)
If all the coefficients are constant with respect to the variable t, the solution of the differential equation accelerated by the impulse function becomes f(t)u(t) and all the initial values are transformed into the coefficients of the impulse function and the derivatives as, ________(4.19)
If all the coefficients are constant with respect to the variable t, the solution of the differential equation accelerated by the impulse function becomes f(t)u(t) and all the initial values are transformed into the coefficients of the impulse function and the derivatives as,
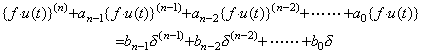 ________(4.20)
The coefficients from b0 to bn−1 are obtained by Theorem 3.4 in Chapter 2 Section 3.6, where the function z is replaced by the function f. The differential equation is transformed into Laplace transform and the solution is expressed in Laplace transform as, ________(4.20)
The coefficients from b0 to bn−1 are obtained by Theorem 3.4 in Chapter 2 Section 3.6, where the function z is replaced by the function f. The differential equation is transformed into Laplace transform and the solution is expressed in Laplace transform as,
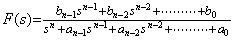 ________(4.21)
Laplace transform of f(t) is Fourier's transform of f(t)u(t)e−at as mentioned in Chapter 2 Section 3.4, where a+jω is replaced by s. Accordingly, substituting zero into a, that is, substituting s=jω into F(s) in Eq. (4.21), F(jω) becomes Fourier's transform of f(t)u(t) and the modulus is the frequency spectrum obtained by the differential analysis. The frequency spectrum is the local frequency spectrum and also the entire frequency spectrum, because the differential equation is identical with Eq. (4.19) everywhere. ________(4.21)
Laplace transform of f(t) is Fourier's transform of f(t)u(t)e−at as mentioned in Chapter 2 Section 3.4, where a+jω is replaced by s. Accordingly, substituting zero into a, that is, substituting s=jω into F(s) in Eq. (4.21), F(jω) becomes Fourier's transform of f(t)u(t) and the modulus is the frequency spectrum obtained by the differential analysis. The frequency spectrum is the local frequency spectrum and also the entire frequency spectrum, because the differential equation is identical with Eq. (4.19) everywhere.
4.4 Theoretical resonance.
. .
When the dumping ratio becomes zero, the electric circuit of the second order system becomes the state of theoretical resonance. If the input f(t) has the component of the resonant frequency ω0, the particular solution x(t) is the sinusoidal function whose amplitude is infinite and the complementary function is superposed on the particular solution as the steady state sinusoidal function of the resonant frequency. If the input f(t) vanishes at any time t1 suddenly by switching off the input circuit, what happens? It is probable that the resonant output vanishes but that the complementary function may remain steady as the pendulum, which keeps on swinging perpetually in case of no friction.
. .
When the output of an electric circuit is expressed in the differential equation Eq. (4.14), supposing the accelerating function is the sinusoidal function of the natural frequency ω0 inputted at t=0 by switching on, the differential equation is expressed in,
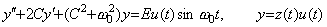 ______(4.22)
Differentiating it twice, it is expressed in the fourth order differential equation accelerated by the impulse function as in Eq. (4.23). ______(4.22)
Differentiating it twice, it is expressed in the fourth order differential equation accelerated by the impulse function as in Eq. (4.23).
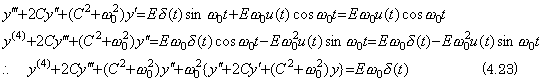 By Theorem 3.4 in Chapter 2 Section 3.6, this is equivalent to,
By Theorem 3.4 in Chapter 2 Section 3.6, this is equivalent to,
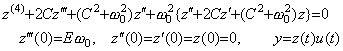 ______(4.24)
The auxiliary equation and its solutions are, ______(4.24)
The auxiliary equation and its solutions are,
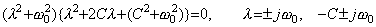 ______(4.25)
Hence, the solution of the differential equation in Eq. (4.24) is, ______(4.25)
Hence, the solution of the differential equation in Eq. (4.24) is,
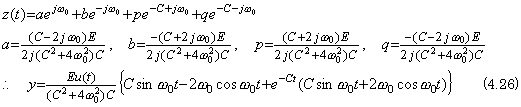 The steady state output is equal to the particular solution x(t) in Eq. (4.16) but the transient output is not equal to the complementary function of the differential equation in Eq. (4.14) because of the additional transient by switching on denoted by u(t).
The steady state output is equal to the particular solution x(t) in Eq. (4.16) but the transient output is not equal to the complementary function of the differential equation in Eq. (4.14) because of the additional transient by switching on denoted by u(t).
. .
When the input vanishes at t1 suddenly by switched off theoretically, the function accelerating the differential equation in Eq. (4.22) becomes,
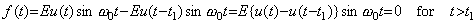 ____(4.27)
Accordingly, the output for t>t1 is superposed negatively by the solution of the following differential equation. ____(4.27)
Accordingly, the output for t>t1 is superposed negatively by the solution of the following differential equation.
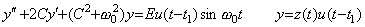 ______(4.28)
Differentiating it twice, it is expressed in the fourth order differential equation accelerated by the impulse function as in Eq. (4.29). ______(4.28)
Differentiating it twice, it is expressed in the fourth order differential equation accelerated by the impulse function as in Eq. (4.29).
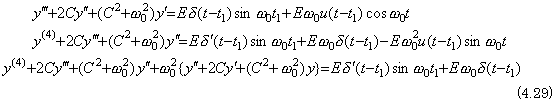 By Theorem 3.4 in Chapter 2 Section 3.6, this is equivalent to,
By Theorem 3.4 in Chapter 2 Section 3.6, this is equivalent to,
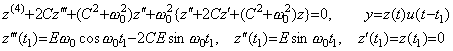 ____(4.30)
The auxiliary equation and its solutions are equal to Eq. (4.25). Hence, the solution of the differential equation in Eq. (4.30) is, ____(4.30)
The auxiliary equation and its solutions are equal to Eq. (4.25). Hence, the solution of the differential equation in Eq. (4.30) is,
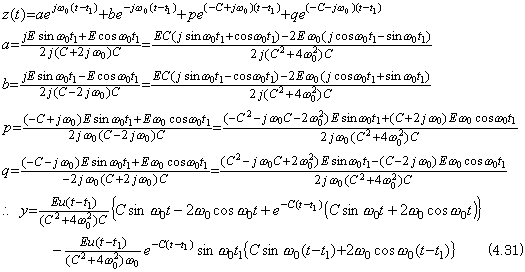 Accordingly, the output in Eq. (4.26) vanishes at t=t1 but the transient output by switching off continues decreasing the amplitude after t1. It is expressed in,
Accordingly, the output in Eq. (4.26) vanishes at t=t1 but the transient output by switching off continues decreasing the amplitude after t1. It is expressed in,
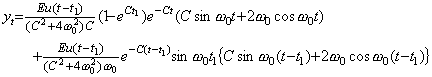 ______(4.32). .
If the electric circuit is in the state of theoretical resonance, the C value of the differential equation in Eq. (4.22) becomes zero so the C value of Eq. (4.23) to Eq. (4.25) becomes zero. Hence, the solutions z(t) and y(t) become, ______(4.32). .
If the electric circuit is in the state of theoretical resonance, the C value of the differential equation in Eq. (4.22) becomes zero so the C value of Eq. (4.23) to Eq. (4.25) becomes zero. Hence, the solutions z(t) and y(t) become,
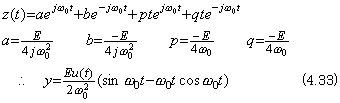 This is equal to the limit of Eq. (4.26) as to the C value which approaches zero. This amplitude is not infinite differently from the case in Eq. (4.16) and increases infinitely because of the transient of switching on. In the same way, the output superposed negatively by switching off is the limit of Eq. (4.31) and it is expressed in,
This is equal to the limit of Eq. (4.26) as to the C value which approaches zero. This amplitude is not infinite differently from the case in Eq. (4.16) and increases infinitely because of the transient of switching on. In the same way, the output superposed negatively by switching off is the limit of Eq. (4.31) and it is expressed in,
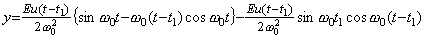 ______(4.34)
Accordingly, the output expressed in Eq. (4.35) continues perpetually after switching off. ______(4.34)
Accordingly, the output expressed in Eq. (4.35) continues perpetually after switching off.
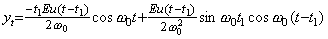 ______(4.35)
However, the energy of the output yt is very small and if the secondary circuit is connected to the load, the output vanishes by the dumping ratio because of the resistance which is yielded in the primary circuit equivalently to the load. It is not possible to store a lot of energy in the resonant circuit made of the superconductor. ______(4.35)
However, the energy of the output yt is very small and if the secondary circuit is connected to the load, the output vanishes by the dumping ratio because of the resistance which is yielded in the primary circuit equivalently to the load. It is not possible to store a lot of energy in the resonant circuit made of the superconductor.
. .
When the electric circuit whose dumping ratio is zero is accelerated by switching on the input of a dumped oscillation as expressed in Eq. (4.36), the output is the solution of the differential equation expressed in Eq. (4.37) and is expressed in Eq. (4.26), because Eq. (4.37) is equal to Eq. (4.23).
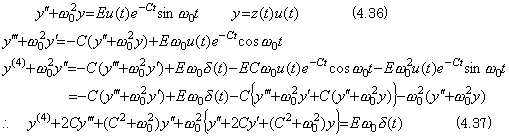 Accordingly, the output of the theoretical resonance accelerated by the dumped oscillation of the natural frequency is equal to the output of the dumped resonance accelerated by the sinusoidal of the natural frequency. The difference between both is that the ratio of the amplitude of output to the amplitude of input increases infinitely in the theoretical resonance. It may be the definition of the theoretical resonance, because it is satisfied also in the case of Eq. (4.33).
Accordingly, the output of the theoretical resonance accelerated by the dumped oscillation of the natural frequency is equal to the output of the dumped resonance accelerated by the sinusoidal of the natural frequency. The difference between both is that the ratio of the amplitude of output to the amplitude of input increases infinitely in the theoretical resonance. It may be the definition of the theoretical resonance, because it is satisfied also in the case of Eq. (4.33).
. .
When the electrical circuit is in a state of dumped resonance and is accelerated by the dumped oscillation of the natural frequency, supposing the both dumping ratios are different, the differential equation is expressed in Eq. (4.38). It is equivalent to the fourth order differential equation in Eq. (4.39) and Eq. (4.40).
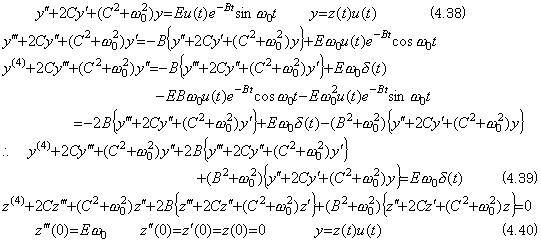 The auxiliary equation and its solutions are,
The auxiliary equation and its solutions are,
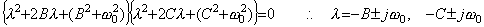 ______(4.41)
Hence, the solution of the differential equation in Eq. (4.40) is, ______(4.41)
Hence, the solution of the differential equation in Eq. (4.40) is,
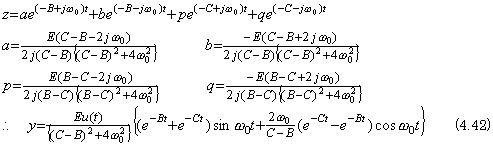 If the C value approaches the B value, the coefficients of the solution z(t) become infinite so it may say the solution is in the state of the theoretical resonance. In the state, the solution y(t) becomes,
If the C value approaches the B value, the coefficients of the solution z(t) become infinite so it may say the solution is in the state of the theoretical resonance. In the state, the solution y(t) becomes,
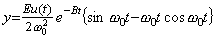 __________(4.43)
This is equal to the theoretical resonance in Eq. (4.33) except e−Bt is multiplied. The output vanishes as the input vanishes. However, the ratio of the amplitude of output to the amplitude of input increases infinitely in the same way as the theoretical resonance in Eq. (4.33). Accordingly, this case is also the theoretical resonance, though nobody recognizes it by now. __________(4.43)
This is equal to the theoretical resonance in Eq. (4.33) except e−Bt is multiplied. The output vanishes as the input vanishes. However, the ratio of the amplitude of output to the amplitude of input increases infinitely in the same way as the theoretical resonance in Eq. (4.33). Accordingly, this case is also the theoretical resonance, though nobody recognizes it by now.
. .
Although this resonance in amplitude vanishes according as the t value increases, if the input is the repeat of the dumped oscillation by a period T as follows, the resonance continues.
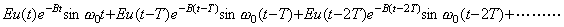 ______(4.44)
The author says the voice uses this continuing resonance, accelerating the vocal tract by the dumped oscillation of the vocal cords. The natural frequency ω0 makes the human hearing recognize the vowels u, o, a, …… as the frequency of light makes the human vision recognize the colors of blue, red, green and so on. The relation of the frequency f given by ω0=2πf to the vowel is shown in Table 4.3. The dumping ratio of everybody is different from others. We can hear the intent voice among the voices of many people by tuning to the dumping ratio. Fig. 4.3 shows the figure of the output in Eq. (4.43) for the input of E=2ω02, ω0=2πf, f=300Hz and B=400, that is, the dumping ratio ζ=2/3π. It is similar to the sonic wave of the vowel u. The human hearing recognizes the values ω0 and B by obtaining the fourth order differential equation in Eq. (4.40) from the initial values at the point where the sonic wave intersects to the axis of zero level. It is the reason why the sonic wave does not lose the character of vowel, even if it is amplified and cut the peak by limiter. These details are treated in Chapter 6. ______(4.44)
The author says the voice uses this continuing resonance, accelerating the vocal tract by the dumped oscillation of the vocal cords. The natural frequency ω0 makes the human hearing recognize the vowels u, o, a, …… as the frequency of light makes the human vision recognize the colors of blue, red, green and so on. The relation of the frequency f given by ω0=2πf to the vowel is shown in Table 4.3. The dumping ratio of everybody is different from others. We can hear the intent voice among the voices of many people by tuning to the dumping ratio. Fig. 4.3 shows the figure of the output in Eq. (4.43) for the input of E=2ω02, ω0=2πf, f=300Hz and B=400, that is, the dumping ratio ζ=2/3π. It is similar to the sonic wave of the vowel u. The human hearing recognizes the values ω0 and B by obtaining the fourth order differential equation in Eq. (4.40) from the initial values at the point where the sonic wave intersects to the axis of zero level. It is the reason why the sonic wave does not lose the character of vowel, even if it is amplified and cut the peak by limiter. These details are treated in Chapter 6.
| Table 4.3 The relation between vowel and frequency. |
|---|
| Vowel | u | o | a | 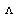 | 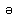 | 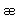 | e | i |
| Frequency(Hz) | 300 | 500 | 700 | 1100 | 1300 | 1700 | 1900 | 2300 |
| Basic Wave(Hz) | *** | *** | *** | 700 | 700 | 700 | 500 | 300 |
| % of Vowel Hz | | | | 50 | 40 | 30 | 20 | 10 |
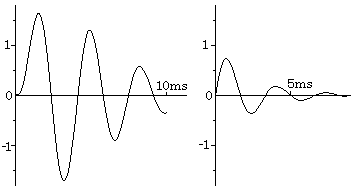
Fig. 4.3 (a) Output___________(b) Input
Return to CONTENTS |
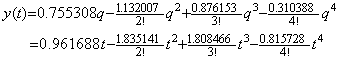 ______(4.1)
______(4.1)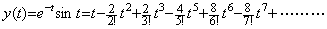 ______(4.2)
______(4.2)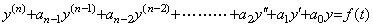 ____(4.3)
____(4.3)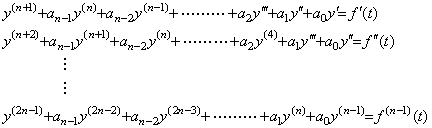 ___(4.4)
___(4.4)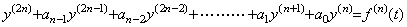 ____(4.5)
____(4.5)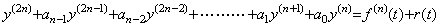 ____(4.6)
____(4.6)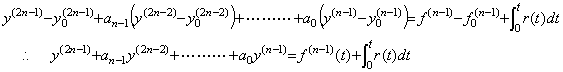

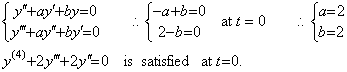
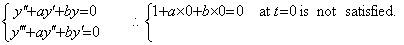
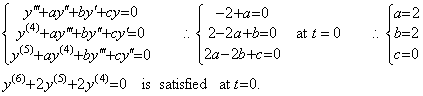
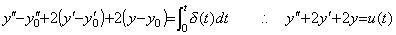 ______(4.7)
______(4.7) ______(4.8)
______(4.8)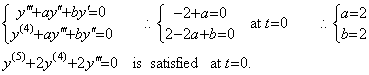
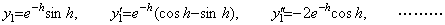
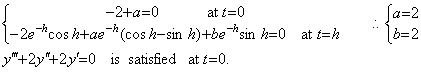
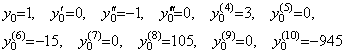
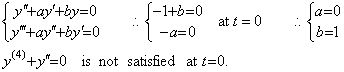
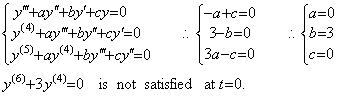
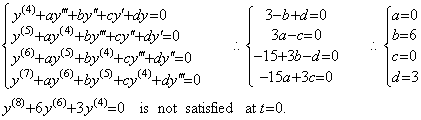
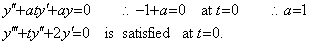
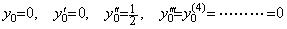
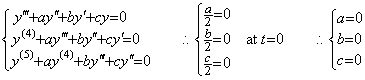
 ________(4.9)
________(4.9)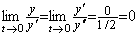
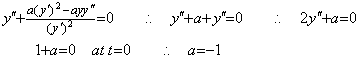
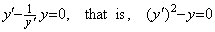 ________(4.10)
________(4.10)
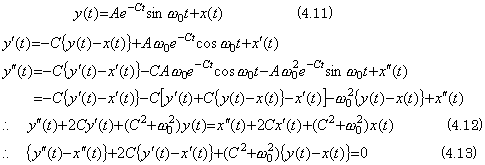
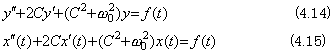
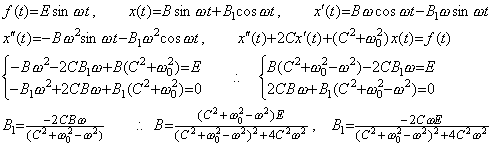 ___(4.16)
___(4.16)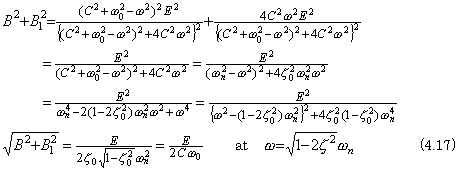
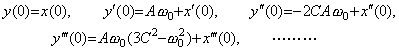
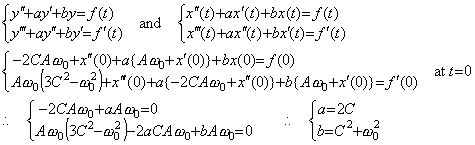

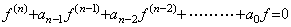 ________(4.19)
________(4.19)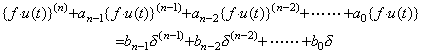 ________(4.20)
________(4.20)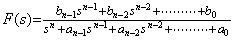 ________(4.21)
________(4.21)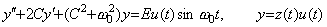 ______(4.22)
______(4.22)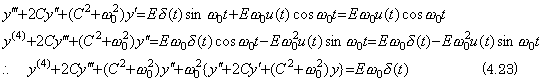
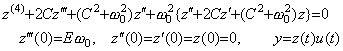 ______(4.24)
______(4.24)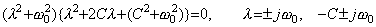 ______(4.25)
______(4.25)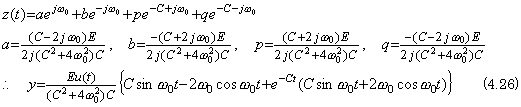
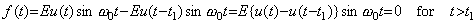 ____(4.27)
____(4.27)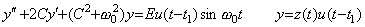 ______(4.28)
______(4.28)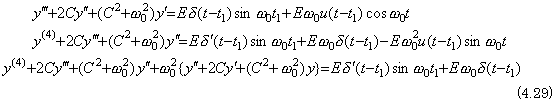
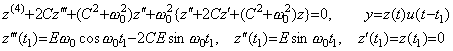 ____(4.30)
____(4.30)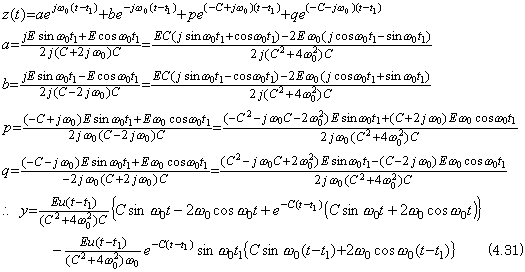
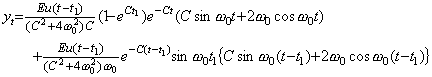 ______(4.32)
______(4.32)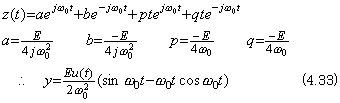
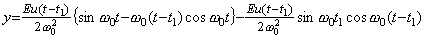 ______(4.34)
______(4.34)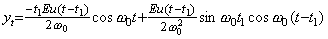 ______(4.35)
______(4.35)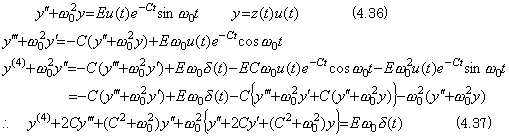
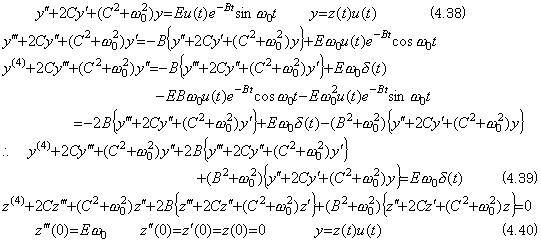
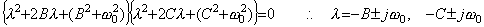 ______(4.41)
______(4.41)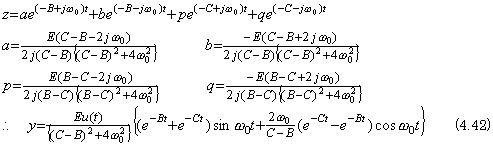
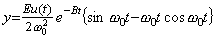 __________(4.43)
__________(4.43)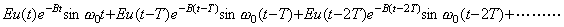 ______(4.44)
______(4.44)