2.1 Reducing the n-th order differential equation to the first order one.
. . Generally, the n-th order differential equation excited by g(t) may be expressed in,
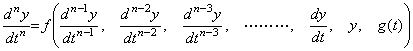 _____(2.1)
_____(2.1)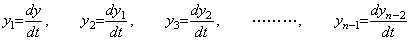 ______(2.2)
______(2.2)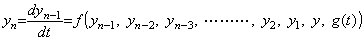 ________(2.3)
________(2.3). . The solution and parameters of the first order differential equation are denoted by the array Y(n) in program as Y(n)=
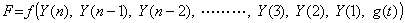 _____(2.4)
_____(2.4)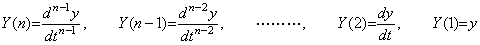 _____(2.5)
_____(2.5)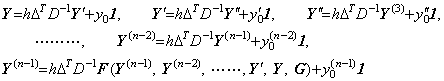 ____(2.6)
____(2.6). . The differential equation in Eq. (2.7) is transformed into the vector equation as expressed in Eq. (2.8).
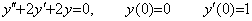 ________(2.7)
________(2.7)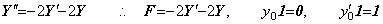 ______(2.8)
______(2.8)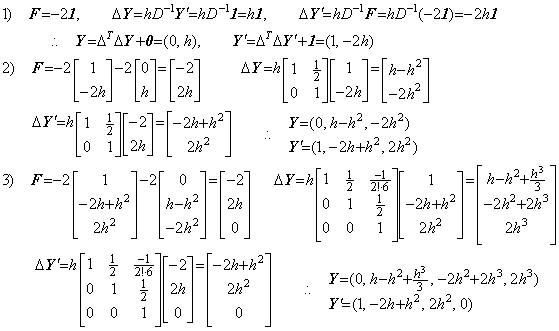
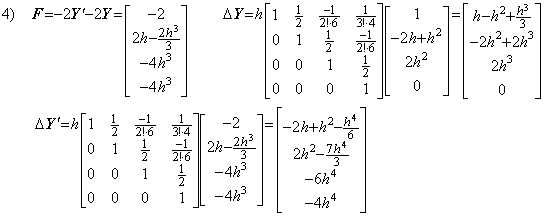
Correcting the results by use of the integral matrix of order (4×5),
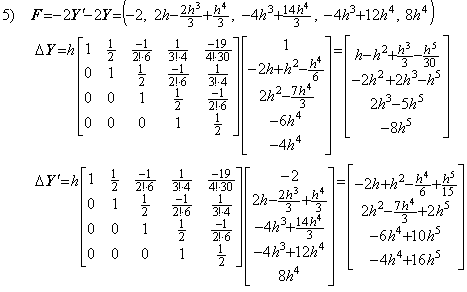
Hence the solutions yk and the derivatives yk' at tk=kh are,
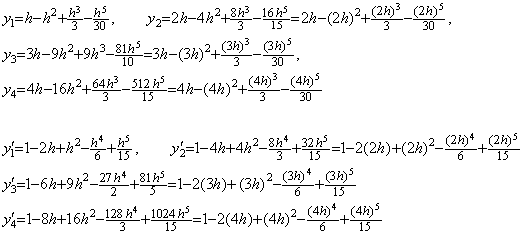
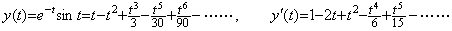 ____(2.9)
____(2.9)
2.2 Some troubles of the n-th order differential equations.
. .
The programs shown in Chapter 2 are what carry out the calculations of the matrix equations by transforming the successive differences into the values of functions y0, y1, y2, ……… and f0, f1, f2, ……… at the equidistant points, which subdivide an integral interval. The equidistant points are denoted by the variable X instead of the variable t in the programs. The program 2.2 in Chapter 2 Section 2.3 uses the three points which are the integral limits and the half point and it varies the integral interval so that the solution has the same accuracy anywhere. Accordingly, it is able to solve the n-th differential equations very accurately. However, it has some troubles, which all the usual methods also have.
. .
Differentiating the first order differential equation in Eq. (2.10), it becomes the second order differential equation in Eq. (2.11).
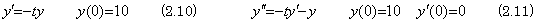
| Table 2.1 The solutions of Eq. (2.10) and Eq. (2.11). | ||||||
|---|---|---|---|---|---|---|
| IB | t | EE | F=-X*Y(1) | EE | F=-X*Y(2)-Y(1) | True values |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 : : : 50 51 52 53 54 55 56 57 58 59 60 : : : 120 121 122 123 124 125 126 127 128 129 130 |
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 : : : 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6.0 : : : 12.0 12.1 12.2 12.3 12.4 12.5 12.6 12.7 12.8 12.9 13.0 |
1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 : : : 8 8 8 8 8 8 8 8 8 8 8 : : : 16 16 16 16 16 16 16 16 16 16 16 |
9.950125E+00 9.801987E+00 9.559975E+00 9.231163E+00 8.824968E+00 8.352701E+00 7.827045E+00 7.261489E+00 6.669767E+00 6.065305E+00 5.460743E+00 4.867521E+00 4.295572E+00 3.753110E+00 3.246524E+00 : : 2.249058E-05 1.343811E-05 7.949388E-06 4.655715E-06 2.699580E-06 1.549755E-06 8.808170E-07 4.956403E-07 2.761243E-07 1.522999E-07 : : 1.612396E-31 4.784174E-32 1.405382E-32 4.087319E-33 1.176915E-33 3.355084E-34 9.469437E-35 2.646041E-35 7.320252E-36 2.005017E-36 |
1 1 1 2 2 2 2 2 2 2 1 1 1 1 1 : : : 8 8 8 8 8 8 8 8 8 8 8 : : : |
9.950125E+00 9.801987E+00 9.559976E+00 9.231164E+00 8.824969E+00 8.352702E+00 7.827045E+00 7.261490E+00 6.669768E+00 6.065306E+00 5.460744E+00 4.867522E+00 4.295573E+00 3.753111E+00 3.246524E+00 : : 2.192061E-05 1.288014E-05 7.402909E-06 4.120230E-06 2.174633E-06 1.034919E-06 3.756925E-07 -1.479670E-10 -2.106806E-07 -3.258539E-07 : : |
9.95012479D+00 9.80198673D+00 9.55997478D+00 9.23116344D+00 8.82496903D+00 8.35270199D+00 7.82704545D+00 7.26149030D+00 6.66976789D+00 6.06530660D+00 5.46074412D+00 4.86752228D+00 4.29557318D+00 3.75311111D+00 3.24652467D+00 : : 2.24905706D-05 1.34381028D-05 7.94938558D-06 4.65571332D-06 2.69957850D-06 1.54975396D-06 8.80816483D-07 4.95639984D-07 2.76124090D-07 1.52299797D-07 : : 1.61239131D-31 4.78415969D-32 1.40537718D-32 4.08730597D-33 1.17691094D-33 3.35507273D-34 9.46940211D-35 2.64603133D-35 7.32022496D-36 2.00500878D-36 |
| Table 2.2 The solutions by Runge-Kutta's method. | |||
|---|---|---|---|
| t | y' =−ty | y"=−ty' −y | True value |
| 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 : : : 5.5 5.6 5.7 5.8 5.9 6.0 6.1 6.2 6.3 6.4 6.5 : : : 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 10.9 11.0 |
9.950125E+00 9.801987E+00 9.559975E+00 9.231163E+00 8.824968E+00 8.352701E+00 7.827044E+00 7.261490E+00 6.669768E+00 6.065307E+00 5.460745E+00 4.867524E+00 4.295576E+00 3.753115E+00 3.246530E+00 2.780380E+00 2.357469E+00 1.978997E+00 1.644756E+00 1.353366E+00 : : 1.559706E-06 8.871572E-07 4.996309E-07 2.786068E-07 1.538263E-07 8.409479E-08 4.552090E-08 2.439828E-08 1.294846E-08 6.804427E-09 : : 9.581400E-22 3.545647E-22 1.300621E-22 4.729557E-23 1.705030E-23 6.094156E-24 2.159702E-24 7.589331E-25 2.644683E-25 9.139807E-26 |
9.950125E+00 9.801988E+00 9.559977E+00 9.231166E+00 8.824972E+00 8.352706E+00 7.827050E+00 7.261496E+00 6.669774E+00 6.065312E+00 5.460750E+00 4.867527E+00 4.295578E+00 3.753114E+00 3.246527E+00 2.780374E+00 2.357461E+00 1.978987E+00 1.644744E+00 1.353352E+00 : : 1.234772E-06 5.692021E-07 1.880868E-07 -2.696017E-08 -1.461062E-07 -2.104837E-07 : : : : : : : : : : : : : : : : : |
9.950124790D+00 9.801986727D+00 9.559974784D+00 9.231163442D+00 8.824969026D+00 8.352701995D+00 7.827045448D+00 7.261490301D+00 6.669767894D+00 6.065306597D+00 5.460744123D+00 4.867522281D+00 4.295573183D+00 3.753111114D+00 3.246524674D+00 2.780372898D+00 2.357460574D+00 1.978986736D+00 1.644744640D+00 1.353352832D+00 : : 1.549753963D-06 8.808164832D-07 4.956399836D-07 2.761240903D-07 1.522997974D-07 8.316707295D-08 4.496341487D-08 2.406719544D-08 1.275406851D-08 6.691586091D-09 : : 7.060058136D-22 2.558597059D-22 9.180119916D-23 3.261007775D-23 1.146876582D-23 3.993321263D-24 1.376617448D-24 4.698345183D-25 1.587572596D-25 5.311092250D-26 |
. . One of the cause is that the solution expressed in symbolical formula has the last term whose coefficient is inaccurate as shown below. It is similar to the last significant decimal place of the product of two values in single precision.
. . Supposing the initial values are Y=1 and Y' =0,
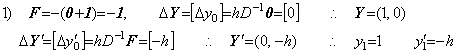
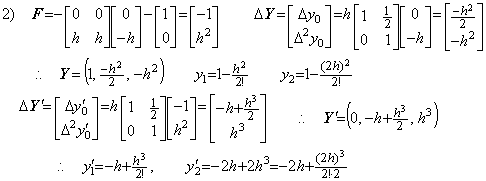
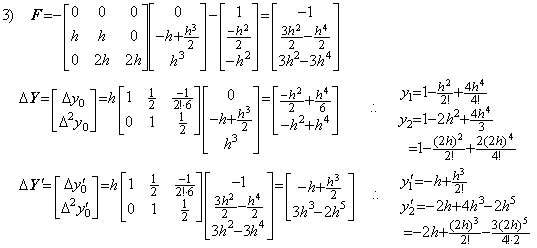
Correcting the results once more by use of the integral matrix of order (2×3),
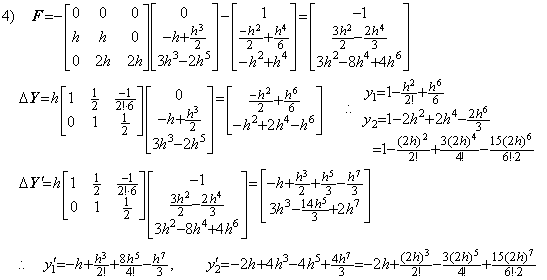
Runge-Kutta's result is of the same as the above result. Denoting the integral interval by 2h and the half interval h for comparison by the same condition,
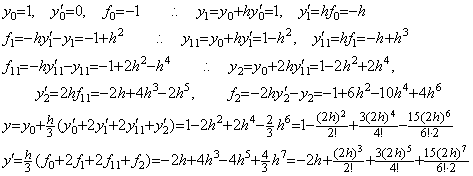
. . Differentiating the first order differential equation in Eq. (2.12), it becomes the second order differential equation expressed in Eq. (2.13) or Eq. (2.14).
 ________(2.12)
________(2.12)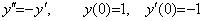 ____(2.13)_______
____(2.13)_______
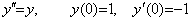 ____(2.14)
____(2.14)Table 2.3 shows the solutions of these differential equations by the author's variable pitch method using 3 points and Runge-Kutta's method. The author's method is able to solve the differential equation in Eq. (2.13) very accurately up to the t value where the solution becomes 10−38 times the initial value y(0). However, it gives very worse solution in case of the differential equation in Eq. (2.14), as if the differential equation has ill condition. Runge-Kutta's method gives similar accurate results for both cases.
| Table 2.3 The solutions of Eq. (2.13) and Eq. (2.14). | ||||
|---|---|---|---|---|
| Author's method | Runge-Kutta | |||
| t | y"=−y' | y"=y | y"=y | True Value |
| 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 : : : 12.5 12.6 12.7 12.8 12.9 13.0 13.1 13.2 13.3 13.4 13.5 13.6 13.7 13.8 13.9 : : : 79.5 79.6 79.7 79.8 79.9 80.0 |
9.048374E-01 8.187308E-01 7.408183E-01 6.703201E-01 6.065307E-01 5.488117E-01 4.965854E-01 4.493290E-01 4.065697E-01 3.678795E-01 3.328711E-01 3.011943E-01 2.725318E-01 2.465970E-01 2.231302E-01 : : : 3.726654E-06 3.372015E-06 3.051127E-06 2.760773E-06 2.498049E-06 2.260330E-06 2.045230E-06 1.850602E-06 1.674493E-06 1.515143E-06 1.370959E-06 1.240495E-06 1.122447E-06 1.015631E-06 9.189808E-07 : : : 2.975701E-35 2.692530E-35 2.436286E-35 2.204447E-35 1.994669E-35 1.804854E-35 |
9.048374E-01 8.187308E-01 7.408183E-01 6.703201E-01 6.065307E-01 5.488117E-01 4.965854E-01 4.493290E-01 4.065697E-01 3.678795E-01 3.328711E-01 3.011943E-01 2.725318E-01 2.465970E-01 2.231302E-01 : : : 3.232717E-06 2.826129E-06 2.447830E-06 2.094027E-06 1.761181E-06 1.445965E-06 1.145217E-06 8.559339E-07 5.752146E-07 3.002523E-07 2.829755E-08 -2.433766E-07 -5.174838E-07 -7.967729E-07 -1.084036E-06 : : : : : : : : : |
9.048375E-01 8.187309E-01 7.408184E-01 6.703203E-01 6.065310E-01 5.488120E-01 4.965857E-01 4.493293E-01 4.065700E-01 3.678798E-01 3.328715E-01 3.011946E-01 2.725322E-01 2.465973E-01 2.231305E-01 : : : 3.726697E-06 3.372055E-06 3.051162E-06 2.760806E-06 2.498080E-06 2.260357E-06 2.045256E-06 1.850624E-06 1.674514E-06 1.515163E-06 1.370976E-06 1.240511E-06 1.122461E-06 1.015645E-06 9.189933E-07 : : : 2.975915E-35 2.692719E-35 2.436473E-35 2.204612E-35 1.994816E-35 1.804984E-35 |
9.04837417D-01 8.18730751D-01 7.40818212D-01 6.70320042D-01 6.06530660D-01 5.48811623D-01 4.96585310D-01 4.49328959D-01 4.06569645D-01 3.67879441D-01 3.32871076D-01 3.01194198D-01 2.72531774D-01 2.46596970D-01 2.23130160D-01 : : : 3.72665317D-06 3.37201395D-06 3.05112614D-06 2.76077205D-06 2.49804890D-06 2.26032941D-06 2.04522984D-06 1.85060155D-06 1.67449289D-06 1.51514325D-06 1.37095909D-06 1.24049461D-06 1.12244658D-06 1.01563128D-06 9.18980832D-07 : : : 2.97569687D-35 2.69252598D-35 2.43628339D-35 2.20444374D-35 1.99466622D-35 1.80485139D-35 |
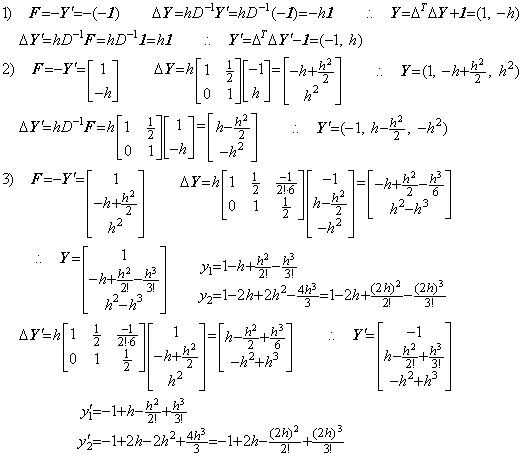
Correcting the results twice more by use of the integral matrix of order (2×3),
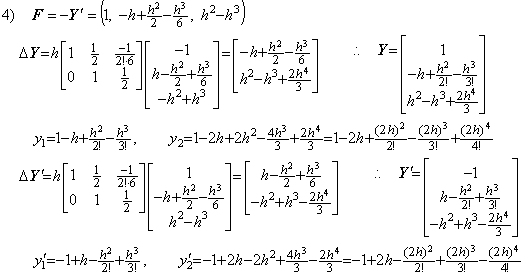
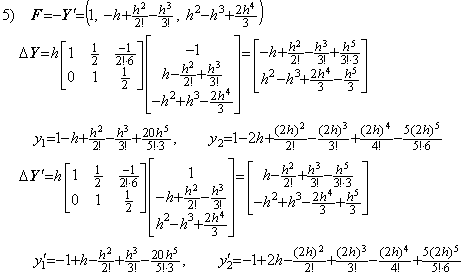
In case of Eq. (2.14), although the vector F is F=Y, it is equal to the above F value of every step because of Y=−Y' . Hence the solutions expressed in symbolical formula are equal to above results. Runge-Kutta's result becomes,
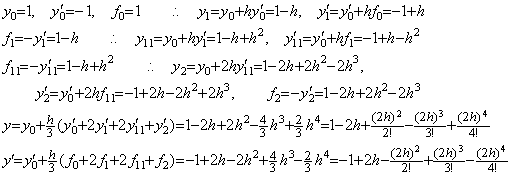
. . However, in case of the differential equation in Eq. (2.14) the value ΔY' is different from the result of the above step 5), because the integrand is F=Y and the Y value obtained in step 4) is equal to the result of the above step 5).
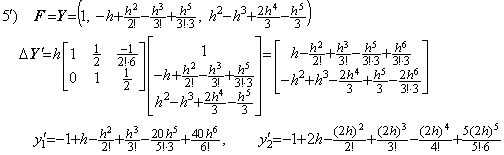
. . The vector ΔY' has the terms of h6 with incorrect coefficients. Although these have an influence on the result y1' , these have no influence on the result y2' by cancellation. However, these are not always canceled for all the t values in numerical calculation and these cause the trouble of the solution of the differential equation y"=y by author's method in Table 2.3. The trouble is solved by changing the order of calculation of ΔY' to ΔY into the order expressed in above step 4) and 5). Accordingly, the integrands of every step must be the results of the preceding step and all the programs in Chapter 2 must be corrected as shown in Table 2.4. However, the correction cannot solve the trouble of the differential equation in Eq. (2.11).
| Table 2.4 The corrections of the programs in Chapter 2. | |
|---|---|
| Program 1 | 34 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:Y(J3)=Y1(J3):NEXT: ___GOSUB 50:GOSUB 52 36 FOR J3=1 TO ND:Y2(J3)=FNY2:Y(J3)=Y2(J3):NEXT |
| Program 2.1 | 36 FOR J3=1 TO ND:Y1(J3)=FNY8:Y2(J3)=FNY9:Y3(J3)=FNY10:Y4(J3)=FNY11: ___Y(J3)=Y1(J3):NEXT:GOSUB 42:GOSUB 44:GOSUB 46:GOSUB 48: ___FOR J3=1 TO ND:Y4(J3)=FNY11:Y(ND)=Y4(ND):NEXT |
| Program 2.2 | 34 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:Y(J3)=Y1(J3):NEXT: ___GOSUB 50:GOSUB 52:R2=Y(ND)*RA 36 FOR J3=1 TO ND:Y2(J3)=FNY2:Y(J3)=Y2(J3):NEXT:R3=Y(ND)*RA |
| Program 2.3 | 40 FOR J3=1 TO ND:Y1(J3)=FNY8:Y2(J3)=FNY9:Y3(J3)=FNY10:Y4(J3)=FNY11: ___Y(J3)=Y1(J3):NEXT:GOSUB 56:GOSUB 58:GOSUB 60:GOSUB 62: ___R2=Y(ND)*RA 42 FOR J3=1 TO ND:Y4(J3)=FNY11:Y(J3)=Y4(J3):NEXT:R3=Y(ND)*RA: ___RA=RM*ABS(R3) |
| Program 2.4 | 34 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:Y(J3)=Y1(J3):NEXT: ___GOSUB 50:GOSUB 52:R2=Y(ND)*RA 36 J3=1 TO ND:Y2(J3)=FNY2:Y(J3)=Y2(J3):NEXT:R3=Y(ND)*RA: ___RA=RM*ABS(R3) |
| Program 4.1 | 36 FOR J=1 TO NF:FOR J3=1 TO ND(J):Y1(J3,J)=FNY1:Y2(J3,J)=FNY2: ___Y(J3,J)=Y1(J3,J):NEXT J3,J:GOSUB 56:GOSUB 58 38 FOR J=1 TO NF:R2(J)=Y(ND(J),J)*RA(J):FOR J3=1 TO ND(J):Y2(J3,J)=FNY2: ___Y(J3,J)=Y2(J3,J):NEXT J3:R3(J)=Y(ND(J),J)*RA(J):RA(J)=RM*ABS(R3(J)): ___NEXT J |
. . When the solution of the second differential equation consists of one fundamental solution which decreases to zero more rapidly than the impulsive response of the differential equation, it generally cannot be solved accurately up to the far point from t=0 as mentioned in Chapter 2 Section 1.7. The impulsive response of the differential equation is the solution of the differential equation driven by the impulse function, where all the initial values are zero. In case of Eq. (2.13) and Eq. (2.14), they are the solutions of,
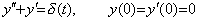 ____(2.15)______
____(2.15)______
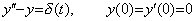 ____(2.16)
____(2.16)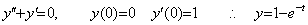 _____(2.17)
_____(2.17)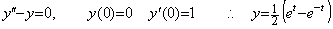 _____(2.18)
_____(2.18). . For example, the first order differential equation in Eq. (2.19) can be solved up to the t value where the solution decreases to 10−38 times the initial value, but the second differential equations in Eq. (2.20) and Eq. (2.21) cannot be solved correctly after the solution decreased to the value less than 10−8 times the initial value in single precision.
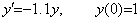 ______(2.19)
______(2.19)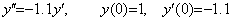 ______(2.20)
______(2.20)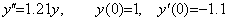 ______(2.21)
______(2.21). . The accuracy of the solution of Eq. (2.20) is improved by the calculation using the variables of double length, even if the coefficient of the differential equation and the initial values are of the single length. Appending "DEFDBL X,Y,F,H:" at the top of Line 10 of Program 1 and giving following subroutines,
| 56 F=-1.1!*Y(2):RETURN 58 XB=0:XE=80:N=800:ND=2:Y(1)=1:Y(2)=-1.1!:RETURN 60 Y#=EXP(-1.1!*X#):RETURN |
The result has no significant figure after it decreased to the less value than 10−17 times the initial value. The reason is that the mantissa consists of three bytes in single precision of the binary system and seven bytes in the double precision and that it corresponds to seven figures and sixteen figures of the decimal system respectively. This shows that the results of the four operations in single precision must not always be rounded off to single length.
. . It is similar to the trouble occurring in the very small root of a quadratic equation which has another large root. The quadratic equation in Eq. (2.22) is expressed in Eq. (2.23), approximating the coefficients in five figures.
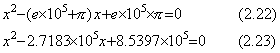
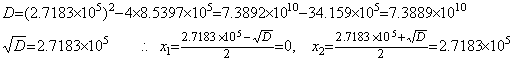
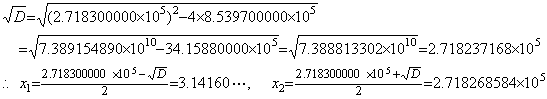
2.3 The solution by use of the operator valued function of the integral operator.
. .
The solution of the n-th order differential equation may be expressed in the n multiple integral as,
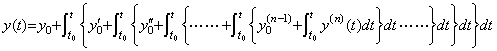 ____(2.24)
____(2.24)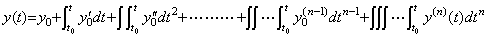 ____(2.25)
____(2.25). . The author's n multiple integral operator obtains the n-th difference of the last term, that is, Δny(t) and all the other terms vanish as mentioned in Theorem 4.18 in Chapter 3 Section 4.7. The vector expression is,
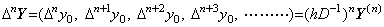 ______(2.26)
______(2.26) __________(2.27)
__________(2.27). . However, in order to obtain the solution y(t), that is, the vector Y, the initial value y0 and the initial differences Δy0, Δ2y0, Δ3y0, ………, Δn−1y0 must be known instead of the initial values. In usual, the differential equation is given the initial values so these must be transformed into the initial differences in order to solve the differential equation by use of the author's n multiple integral operator. The transformation is expressed by Eq. (1.34) in,
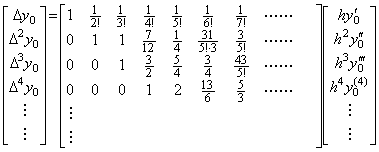 __(2.28)
__(2.28)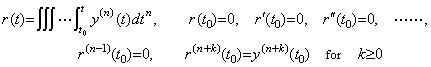 ____(2.29)
____(2.29)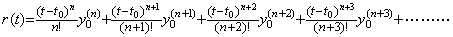 ____(2.30)
____(2.30). . The author's n multiple integral operator obtains the differences of r(t) equal to and higher than Δnr0=Δny0. In order to correct the initial differences, the differences of r(t) must be transformed into the derivatives higher than the last initial value. The transformation is expressed in the matrix equation whose matrix is constructed from the first rows of the differential operators of successive order, that is, from Table 3.2 in Chapter 3 Section 3.7.
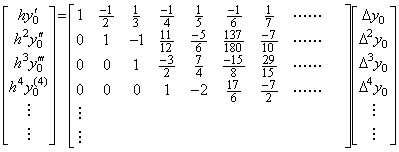 __(2.31)
__(2.31)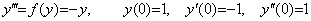 ______(2.32)
______(2.32) ______(2.33)
______(2.33)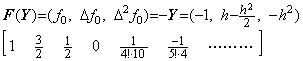
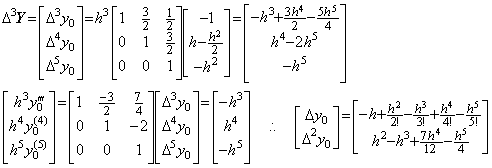 ____(2.34)
____(2.34)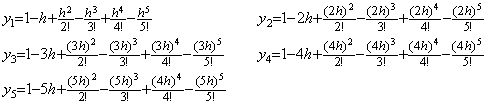 ____(2.35)
____(2.35)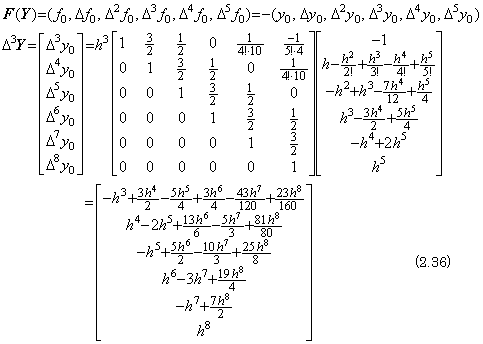
| Table 2.5 Expansion of Table 3.2 in Chapter 3 Section 3.7. |
|---|
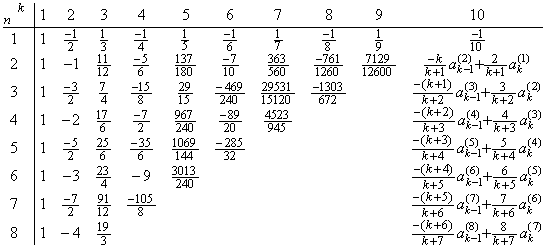
|
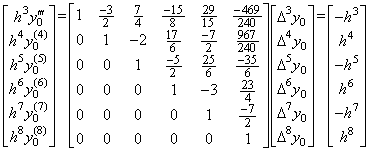 ____(2.37)
____(2.37)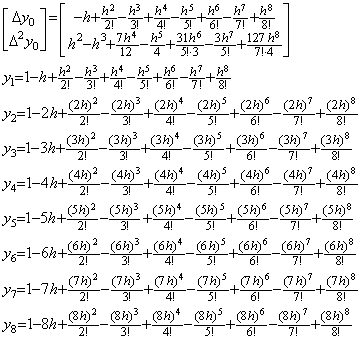 ____(2.38)
____(2.38). . The operation in Eq. (2.31) is the inverse operation to the operation in Eq. (2.28). The integral results Δ3Y in Eq. (2.34) and Eq. (2.36) are equivalent to the results obtained by Taylor's expansion, that is, by Eq. (2.28). Accordingly, it has no meaning to correct the results Δ3Y by use of the results of Eq. (2.31). However, it is significant to correct the predicted initial derivatives Δy0 and Δ2y0 by the results, because they are predicted by use of hy0' and h2y0" only. This is shown by dividing the matrix in Eq. (2.28) into two matrices as follows.
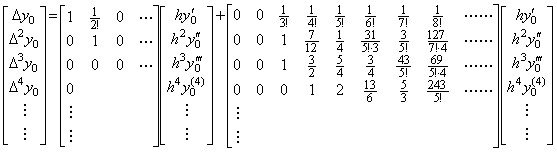 __(2.39)
__(2.39)
. . The correction also may be carried out by use of the matrix of Eq. (2.31), even if the differential equation is of any order. Dividing the matrix of Eq. (2.31) into the unit matrix and the remainder part and exchanging the first term ΔY for the left side,
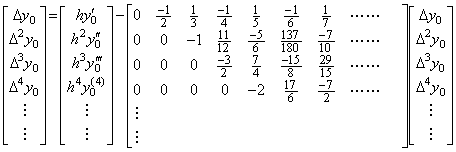 ____(2.41)
____(2.41). . Substituting the result Δ3Y expressed in Eq. (2.34) and the initial values y0' =−1, y0"=1 into Eq. (2.41),
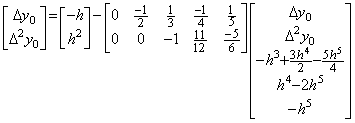
2.4 The solution of the n-th order differential equation with constant coefficients.
. .
The third order differential equation in Eq. (2.42) has the same solution as the third order differential equation in Eq. (2.32)
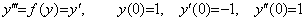 ________(2.42)
________(2.42)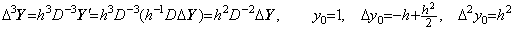 ____(2.43)
____(2.43)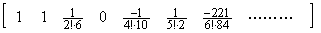
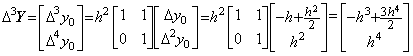 ____(2.44)
____(2.44)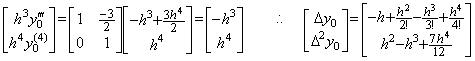 ___(2.45)
___(2.45)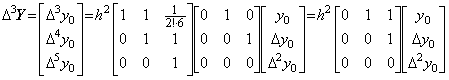 ____(2.46)
____(2.46)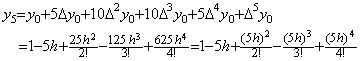 ______(2.47)
______(2.47)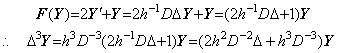 ______(2.48)
______(2.48)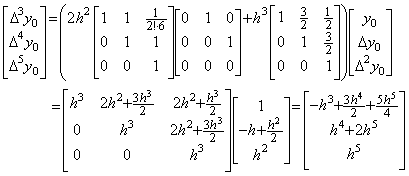 ____(2.49)
____(2.49)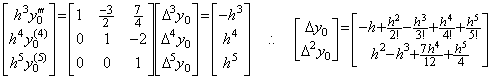 ____(2.50)
____(2.50)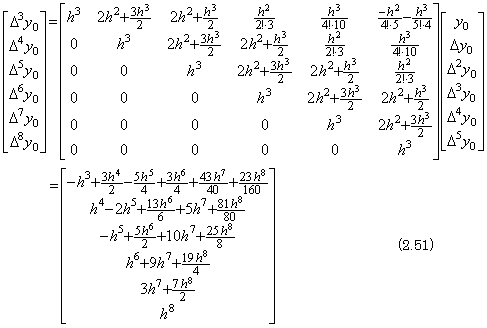
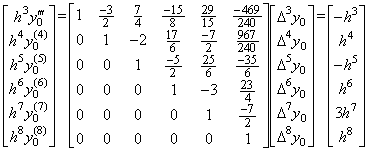 ____(2.52)
____(2.52)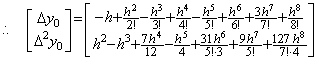 ______(2.53)
______(2.53). . In general, the n-th order differential equation with constant coefficients is expressed in,
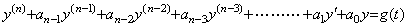 ____(2.54)
____(2.54)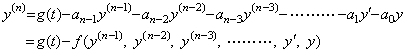 ____(2.55)
____(2.55)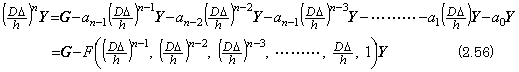
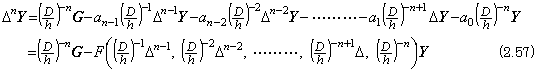
. . The solution Y has some error at the tail term as shown in Eq. (2.49), if the function f has the solution y and the derivatives. However, the numerical result converges on the sufficiently accurate solution, if the accelerating function g(t) is the impulse function δ(t) or any function except of the derivatives of the impulse function and if the initial values are not equivalent to accelerating the differential equation by the derivatives of the impulse function, when the initial values are transformed into the equivalent accelerating functions by Eq. (3.38) in Chapter 2 Section 3.6.
. . The cause of the error is the derivatives of y and not the integral operator. The integrand F(Y) in Eq. (2.48) becomes,
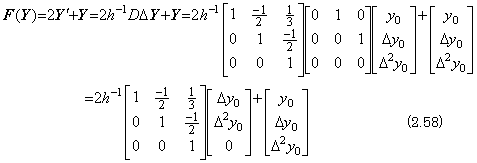

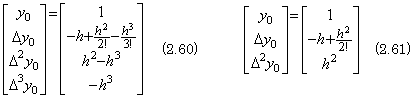
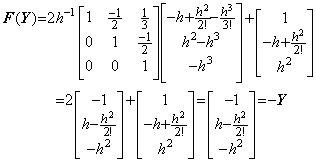 _____(2.62)
_____(2.62). . When the initial values are y0=0, y0' =0, y0"=1, the third difference Δ3y0 is zero because of y0(3)=0 and the two vector values Y in Eq. (2.59) are equivalent. Accordingly, Eq. (2.59) is equivalent to Eq. (2.58) and the result by Eq. (2.57) has no error up to the last term as,
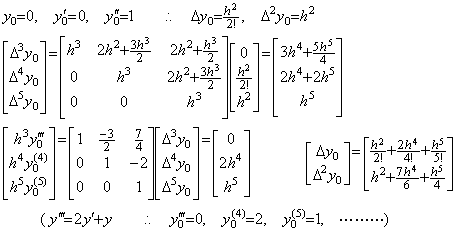 ____(2.63)
____(2.63)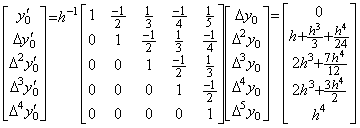 ____(2.64)
____(2.64) . .(2.65)
. .(2.65)
2.5 The n multiple integral by the solution of the first order differential equation.
. .
The integral matrix D3 obtaining Δ3Y in Eq. (2.34) is equal to D×D×D as,
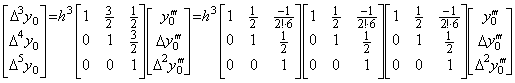 ___(2.66)
___(2.66) ____(2.67)
____(2.67)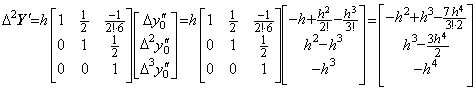 ____(2.68)
____(2.68)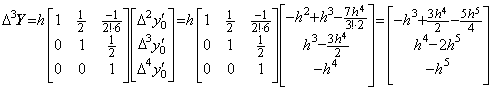 ____(2.69)
____(2.69). . The difference Δy0' may be obtained by integrating the vector ΔY" obtained by Eq. (2.67) together with the initial value y0" and the integral is expressed together with Eq. (2.68) in,
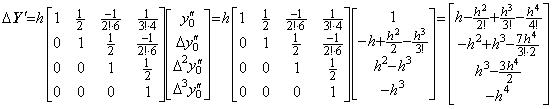 __(2.70)
__(2.70)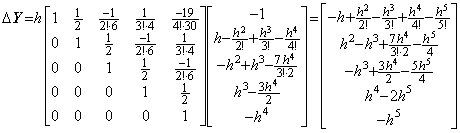 ____(2.71)
____(2.71). . However, if the function f(y) has the derivatives of y as Eq. (2.48), the integral of F(Y) has some error at the last some terms due to the error of F(Y) as mentioned in the preceding section. In order to avoid the error, the integrated result
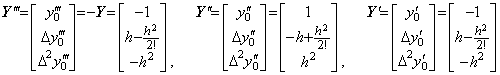 __(2.72)
__(2.72)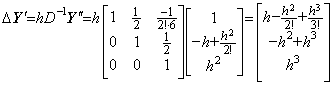 ______(2.73)
______(2.73)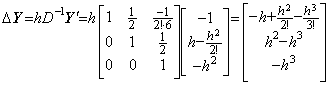 ______(2.74)
______(2.74). . This method is very simple because it is able to start the calculation by the initial values only, increasing the order of the integral matrix by every iteration. However, there does not exist the exact relation as to the integral and integrand between these results Y", Y' , Y. If the result ΔY" in Eq. (2.67) has been convergent, the last correction of ΔY' and ΔY should be carried out by Eq. (2.70) and (2.71) instead of Eq. (2.73) and (2.74), where Δ4y0' Δ4y0 Δ5y0 are ignored when the integral range is shifted to the next range.
2.6 The condition which must be satisfied for the numerical solution to converge.
. .
The n-th order differential equation with constant coefficients in Eq. (2.54) or (2.56) has the solution expressed in Eq. (2.57) but the iterative method must give the fixed point. It requires that the mapping expressed in Eq. (2.57) is a contraction. Denoting two vectors by Y and Z, where the initial values are equal, that is, y0=z0,
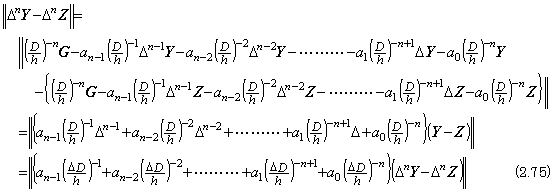
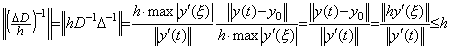 _____(2.76)
_____(2.76) ______(2.77)
______(2.77) ______(2.78)
______(2.78) ______(2.79)
______(2.79)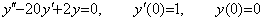 ________(2.80)
________(2.80)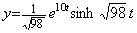 ________(2.81)
________(2.81)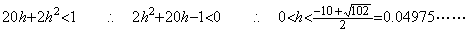 ____(2.82)
____(2.82). . If the integral interval is minus the condition Eq. (2.78) must be expressed in |h| instead of h. Accordingly, Eq. (2.82) becomes as,
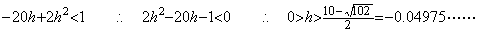 _____(2.83)
_____(2.83). . In general, when the n-th differential equation is expressed in Eq. (2.1), the author's operational calculus express the solution in Eq. (2.6). The last equation must be solved by the iterative method, because the both sides have the vector Y(n−1). Denoting two vectors by Y(n−1) and Z(n−1), where the initial values are equal, that is, y0(n−1)=z0(n−1),
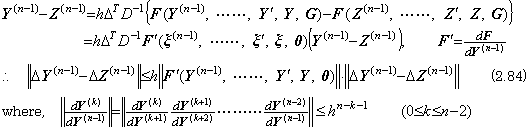
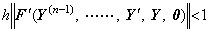 ______(2.85)
______(2.85)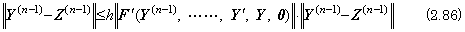
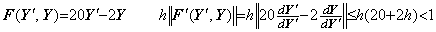 ______(2.87)
______(2.87)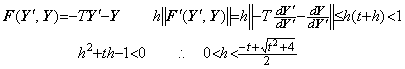 ____(2.88)
____(2.88). . If the integral interval is minus and the t value is positive, the condition Eq. (2.85) must be expressed in |h| instead of h. Accordingly, Eq. (2.88) becomes as,
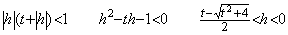 ________(2.89)
________(2.89)