|
5. The operator space.
5.1 The vector space.
. .
The numerical calculus has no irrational number but it is able to carry out the approximate calculations of irrational numbers and functions by use of the nearly equal rational numbers and functions. This operational calculus also has no vector and no operator corresponding to irrational numbers and functions but it is able to treat these by use of the nearly equal vectors and vector valued functions. It is also able to treat complex numbers and functions by use of the ordered pares of two vectors.
. .
The square root of a number a is defined as the number which becomes the number a by being squared. In a similar way, the square root of a function y(t) is defined as the function which becomes the function y(t) by being squared. Denoting it by z(t), there is the relation zk2=yk between the values of the functions at the equidistant points t=t0+kh for k=0, 1, 2, ………. Calculating the successive differences of the both sides, the right side becomes the components of the vector Y and the left side becomes the components of the vector denoting the function z2(t). The latter are equal to the components of the product of the vector Z×Z. Therefore the square root of the vector Y is defined as the vector which becomes the vector Y by being squared. The vector Z may be obtained by calculating the successive differences of zk for k=0, 1, 2, ……… or it can also be obtained by Newton-Raphson's method using this operational calculus.
. .
When the function y(t) is a quadratic function, the square root z(t) becomes the function of infinite degree in Taylor's expansion except for the case that the discriminant of the quadratic equation y(t)=0 vanishes. Accordingly, the square root of the vector has infinite components and exists on the vector space of infinite dimensions. Such vector can be treated in mathematical equations using the vector symbol. The numerical calculus is obliged to truncate the number of components into the first p components from z0 to Δp−1z0, if all the other components can be ignored as the remainder of Newton's interpolation formula. Accordingly, there exist all the vectors on the p dimensional metric space Rp if the p value is the largest dimension of all the vectors.
. .
The truncation of dimensions means that the vector on the metric space R∞ is projected on the subspace Rp as orthogonal projection, because it is equivalent to setting zeros on all the components on the outer space of Rp. If the locus of a sequence of vectors is continuous on the three dimensional Euclidean space, the orthogonal projection on the two dimensional space is also continuous because it only sets zeros to the third components of the vectors and does not remove the vectors whose third components are not zero. In a similar way, if a sequence of vectors is continuous on this metric space R∞, the orthogonal projection on the subspace Rp hold the continuity.
. .
The author defined the magnitude of a vector Y by the norm of the function y(t) in Section 1.2. As the absolute value of a real number is also a real number, so the magnitude of a vector is also the vector which denotes the constant function because of |y(t)|≤||y(t)|| on a given closed interval. Accordingly, he defines the metric between two vectors Y and Z on the metric space by the constant vector which denotes the norm of the difference of functions ||y(t)−z(t)||. The magnitude of vector and the metric may be denoted by the numeric values if it is easy to understand, because this operational calculus does not distinguish between the constant vector and the numeric values. The absolute notation of the vector |Y| denotes the function |y(t)|. In a similar way, the magnitude of the vector is denoted by the norm of the vector ||Y|| because of ||y(t)||. Hence,
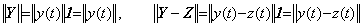 _____(5.1). .
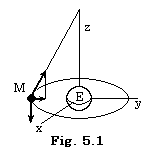
If we view the phenomena occurring on the space Rp+1 as the phenomena on the space Rp, it seems as if there exist such phenomena as do not exist really on the space Rp. Let us consider the pendulum system on the three dimensional Euclidean space as shown in Fig. 5.1, where the gravitation is vertical to the x-y plane and the pendulum is being swung so that the weight of pendulum turns around the origin. Let us name the weight of pendulum Moon and name the sphere on the origin Earth. If we are on the two dimensional space expressed in the x-y plane, we see that Moon turns around Earth but does not see the rod of pendulum and the gravitation and we see that Moon falls to Earth if Moon stops to turn around Earth. Though Moon is not joined to Earth by rod, there exists the force joining both. It seems as if there exists the universal gravitation, otherwise it may be visible that Earth and Moon are joined by the miracle rod, which is the orthogonal projection of the rod of pendulum and which is visible but cannot touch. In reality, we are on the three dimensional space and we see that the centripetal force is the orthogonal projection of the tension in the rod of pendulum on the x-y plane. Now it is assumed that we exist on the two dimensional space and we wish to obtain the true force working to Moon, that is, the tension in the rod of pendulum on the three dimensional space. However, we cannot know the z-axis component of the tension, because it is orthogonal to the x-y plane. It is also not able to infer it from the component on the x-y plane. In order to find out the true force working to Moon, we must go out on the three dimensional space. _____(5.1). .
If we view the phenomena occurring on the space Rp+1 as the phenomena on the space Rp, it seems as if there exist such phenomena as do not exist really on the space Rp. Let us consider the pendulum system on the three dimensional Euclidean space as shown in Fig. 5.1, where the gravitation is vertical to the x-y plane and the pendulum is being swung so that the weight of pendulum turns around the origin. Let us name the weight of pendulum Moon and name the sphere on the origin Earth. If we are on the two dimensional space expressed in the x-y plane, we see that Moon turns around Earth but does not see the rod of pendulum and the gravitation and we see that Moon falls to Earth if Moon stops to turn around Earth. Though Moon is not joined to Earth by rod, there exists the force joining both. It seems as if there exists the universal gravitation, otherwise it may be visible that Earth and Moon are joined by the miracle rod, which is the orthogonal projection of the rod of pendulum and which is visible but cannot touch. In reality, we are on the three dimensional space and we see that the centripetal force is the orthogonal projection of the tension in the rod of pendulum on the x-y plane. Now it is assumed that we exist on the two dimensional space and we wish to obtain the true force working to Moon, that is, the tension in the rod of pendulum on the three dimensional space. However, we cannot know the z-axis component of the tension, because it is orthogonal to the x-y plane. It is also not able to infer it from the component on the x-y plane. In order to find out the true force working to Moon, we must go out on the three dimensional space.
. .
Similar phenomena are caused on this vector space too by the remainder of Newton's interpolation formula. In this operational calculus, it is supposed that the function satisfies y(t)∈Cp+1[a, b]. Hence all the vectors exist on the p+1 dimensional space and the remainder exists on the outer space. Denoting the vector on the space R∞ by Y and the projection on the space Rp+1 by Z, the remainder is Y−Z and orthogonal to the space Rp+1, so the orthogonal projection of the remainder is zero on the space Rp+1. The vector Z is the sub vector of the vector Y on the space Rp+1 but the function z(t) expressed in the vector Z is not equal to the function y(t) expressed in the vector Y except for the equidistant points. By Newton's interpolation formula it is required to add the remainder term in order that both are equal at all the points. The remainder term is what is determined by the elements of the vector Y−Z, that is, the elements of the vector Y on the outer space of the space Rp+1, and what does not exist on the space Rp+1. It is not possible to know the quantity if we are on the space Rp+1. If we go out from the space Rp+1, that is, if we compare the interpolation with Newton's interpolation formula of higher order, we can surmise that the remainder is about equal to the difference.
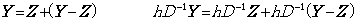 _____(5.1a). .
The product of the integral operator and the vector Y is expressed in (5.1a) using the product of the integral operator and the vector Z. The vector Y−Z consists of the components on the outer space of the space Rp+1, so Eq. (5.1a) seems to express that the sub vector of the vector hD−1Y on the space Rp+1 is equal to the vector hD−1Z. However, the integral formula with remainder expressed in Eq. (4.28) in the section 4.4 denotes that the sum of the vector hD−1Z and the compensation by the product of the integral operator and the remainder Y−Z is equal to the sub vector of the vector hD−1Y on the space Rp+1. The case that both are equal without this compensation is only the case Y=Z, that is, Y is the vector on the space Rp+1. This denotes that in order to obtain the solution of the differential equation the iterative method on the space Rp+1 does not all ways converge to the orthogonal projection of the true solution on the space Rp+1. The correct iterative method must compare the predicted and corrected values on the now space with those on the higher dimensional space by one dimension at least. Or it is able to obtain the equivalent result by using narrower equidistant interval. That the predictor-corrector method as Milne's method repeats the corrector of fixed order many a time means to obtain the result converging to the solution with zero remainder term. If the remainder term is not ignored the solution runs away from the true solution as a matter of course. It is not a matter of stability of the method. _____(5.1a). .
The product of the integral operator and the vector Y is expressed in (5.1a) using the product of the integral operator and the vector Z. The vector Y−Z consists of the components on the outer space of the space Rp+1, so Eq. (5.1a) seems to express that the sub vector of the vector hD−1Y on the space Rp+1 is equal to the vector hD−1Z. However, the integral formula with remainder expressed in Eq. (4.28) in the section 4.4 denotes that the sum of the vector hD−1Z and the compensation by the product of the integral operator and the remainder Y−Z is equal to the sub vector of the vector hD−1Y on the space Rp+1. The case that both are equal without this compensation is only the case Y=Z, that is, Y is the vector on the space Rp+1. This denotes that in order to obtain the solution of the differential equation the iterative method on the space Rp+1 does not all ways converge to the orthogonal projection of the true solution on the space Rp+1. The correct iterative method must compare the predicted and corrected values on the now space with those on the higher dimensional space by one dimension at least. Or it is able to obtain the equivalent result by using narrower equidistant interval. That the predictor-corrector method as Milne's method repeats the corrector of fixed order many a time means to obtain the result converging to the solution with zero remainder term. If the remainder term is not ignored the solution runs away from the true solution as a matter of course. It is not a matter of stability of the method.
. .
Usually, it is said that Runge K. method is stable. It is stable than Milne's method because it increases the degree approximating the solution in order of Euler's method, trapezoidal method, and Simpson's method as author's method. However, the usual arguments about the method being stable or not are meaningless. As example comparing both, the numerical solution of the differential equation (A) described below is shown often. It is shown in the column (A) of Table 5.1, which is the results by Java using the equidistant interval h=0.1 and the calculation with single precision. Java calculates the data with single precision by use of double length if these still in progress are not substituted to the variable of single length, so the results have slightly higher accuracy than BASIC or others. Although the solutions in the column (A) have two significant figures at t=7.0, the results by Milne's method begin to run away from the true solution about at t=5. However, only in the case of the first differential equation it may be said that Runge K. method is stable. The differential equation expressed in (B) is obtained by differentiating the differential equation expressed in (A). As shown in the column (B) of Table 5.1, the solutions begin a loss of accuracy of the last place about at t=0.3, begin to run away about at t=5.7 as the results of Milne's method and reach true solutions times 1000 at t=7.0. The differential equation expressed in (C) is obtained by differentiating the differential equation expressed in (B). As shown in the column (C) of Table 5.1, the solutions lose more accuracy than (B) about at t=0.3, become twice results of (B) about at t=5.6 and reach true solutions times 3000 at t=7.0. The usual argument that the approximation of fixed degree is enough for the numerical method solving differential equations is in the wrong.
| Table 5.1 The solutions for (A), (B) and (C) by Runge K. (Java) |
|---|
| t | (A) | (B) | (C) | 10exp(−t2/2) |
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
:
:
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
6.0
:
:
7.0 |
10.0
9.950125
9.801987
9.559975
9.231163
8.824968
8.352701
7.8270445
7.26149
6.669768
6.0653067
:
:
1.3491768E−5
7.985243E−6
4.679384E−6
2.7150177E−6
1.5597049E−6
8.871567E−7
4.996307E−7
2.786066E−7
1.5382618E−7
:
:
2.3525334E−10 |
10.0
9.950125
9.801988
9.559977
9.231166
8.824973
8.352707
7.827051
7.261497
6.669775
6.0653133
:
:
1.31268E−5
7.6325705E−6
4.33697E−6
2.381408E−6
1.2338529E−6
5.683E−7
1.8720138E−7
−2.7829543E−8
−1.4696013E−7
:
:
−2.5513947E−7 |
10.0
9.950125
9.801988
9.5599785
9.231171
8.82498
8.352717
7.8270645
7.2615128
6.669793
6.0653334
:
:
1.4252864E−5
8.749632E−6
5.4440843E−6
3.4780796E−6
2.3198932E−6
1.6437227E−6
1.2521507E−6
1.02687E−6
8.977589E−7
:
:
7.0546184E−7 |
10.0
9.950124790
9.801986727
9.559974784
9.231163442
8.824969026
8.352701995
7.827045448
7.261490301
6.669767894
6.065306597
:
:
1.343810278E-5
7.949385579E-6
4.655713318E-6
2.699578503E-6
1.549753963E-6
8.808164832E-7
4.956399836E-7
2.761240903E-7
1.522997974E-7
:
:
2.289734846E-10 |
. .
The usual predictor-corrector methods as Milne's method are based on the two incorrect ideas. One of these is the idea that the solution will converge to the accurate value by iterating the approximate formula of fixed degree and by using fixed equidistant interval. Another is the idea using the corrector of lower degree than the predictor. The idea means that the corrector losses the accuracy obtained by the predictor. It only is right that it compares the results of the integral formula with different degree but the iteration of the corrector after this is meaningless.
5.2 The problems about the operator value and the norm.
. .
In usual differential and integral operations, the definitions are not varied by the variable t or by changing the function of operand too. This means that the operator value is a constant value because the rule that makes the resultant function correspond to the function of operand does not vary according to change of the operand. The function f(t) is the operation of the rule f for the independent variable t. For example, in the cubic function t3, the function f is the rule multiplying three t together, or multiplying t by t2. In both, the multiplier varies according to the independent variable t, so this rule varies according to the independent variable t. The constant function is the rule that always makes a constant value correspond to the independent variable t, so the rule does not vary by varying the independent variable t. The rule that the differential or integral operator makes the resultant function correspond to the function of operand is the same as this. The difference of operator corresponds to the difference of function, because it is the difference of rule or definition and every operator corresponds to the constant function, because the definition does not vary by changing the function of operand, which corresponds to the independent variable t. Accordingly, the difference of every operator corresponds to the difference of constant values of constant functions. In usual abstract arguments, it is said that the integral operator has an upper limit but that the differential operator has not any upper limit. It has no meaning at all.
. .
When the operand is atn (n≠−1), the integral operator is equivalent to the function as follows.
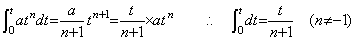 _____(5.2)
In usual arguments as to the integral and differential operators, this function is considered as the operator value of the integral operator. This operator value does not vary everywhere the upper limit of integration is, if the n value of the operand does not change. Accordingly, it is possible to obtain the integral from t0 to t by multiplying this operator value. _____(5.2)
In usual arguments as to the integral and differential operators, this function is considered as the operator value of the integral operator. This operator value does not vary everywhere the upper limit of integration is, if the n value of the operand does not change. Accordingly, it is possible to obtain the integral from t0 to t by multiplying this operator value.
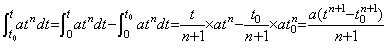 ____(5.3)
If the n value changes, it seems that the operator value changes. However, there is no difference from the linear function, which has different inclination. Hence the operator value is of the same as a letter is of the same even if it has inclination. The operator has the constant operator value but changes its coefficient according as the function of the operand. The difference of inclination is not the difference of the operator value because the definition of integral does not change. This distinguishes the operator from the function. ____(5.3)
If the n value changes, it seems that the operator value changes. However, there is no difference from the linear function, which has different inclination. Hence the operator value is of the same as a letter is of the same even if it has inclination. The operator has the constant operator value but changes its coefficient according as the function of the operand. The difference of inclination is not the difference of the operator value because the definition of integral does not change. This distinguishes the operator from the function.
. .
Supposing that the n value is the difference of the operator value, the operator value becomes infinite value if the n value approaches −1, and the norm of integral operator come not to exist. Because the n value is no part of the operator value, it is correct that the function t with n=0 is the value of integral operator. This operator value does not vary by changing the function of operand, so the norm of integral operator also is the function t. In order that the product of the norms of operator and operand does not become negative when the upper limit of integral is negative, the function |t| becomes the norm of integral operator. As the absolute value of real number is real number, so the norm of operator value is also the operator value.
. .
The operational calculus explicitly shows that the operator value is constant value. Laplace transform and Mikusinski's operational calculus define the multiplication of two functions as the convolution integral. Accordingly, the operator value of the integral operator is a function such that the convolution integral becomes the integral of the integrand. The function is denoted by s−1 in Laplace transform, that is, it is the unit step function u(t). The operator value does not change even if the integrand changes, that is, it is constant value. Denoting the multiplication by the symbol * and using the impulse function and the unit step function defined in Chapter 2 Section 3,
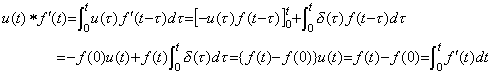 __(5.4)
In case of the function and derivative denoted by f(t)u(t) and f '(t)u(t), using u(t)=1 in the integrand because the value t is the upper limit of the integration, __(5.4)
In case of the function and derivative denoted by f(t)u(t) and f '(t)u(t), using u(t)=1 in the integrand because the value t is the upper limit of the integration,
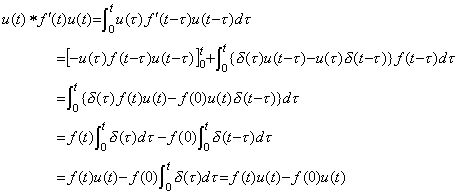 __(5.5)
This is equal to the integral of f' (t)u(t), because, __(5.5)
This is equal to the integral of f' (t)u(t), because,
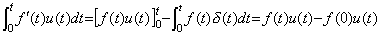 _____(5.6)
Mikusinski denotes the functions f(t)u(t) and f' (t)u(t) by {f(t)}, {f' (t)} and the operator value of the integral operator or the unit step function by {1}. _____(5.6)
Mikusinski denotes the functions f(t)u(t) and f' (t)u(t) by {f(t)}, {f' (t)} and the operator value of the integral operator or the unit step function by {1}.
. .
The norm of the operator value is also the unit step function because,
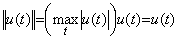 ________(5.7)
The multiplication of the norm of the operator value and the norm of the operand must also be carried out by the convolution integral. ________(5.7)
The multiplication of the norm of the operator value and the norm of the operand must also be carried out by the convolution integral.
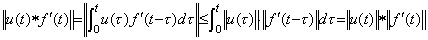 ____(5.8)
Accordingly, expressing the product of the norm in usual multiplication, the norm of integral operator becomes t as follows. ____(5.8)
Accordingly, expressing the product of the norm in usual multiplication, the norm of integral operator becomes t as follows.
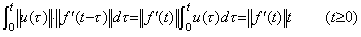 _____(5.9). .
In Theorem 1.1 in Chapter 2 Section 1.5, the author showed that the norm of the integral operator is h when the interval is [t, t+h]. If the interval is [t0, t] the following theorem holds. However, it does not mean that the value of integral operator varies. The definition of integral is the integration from lower limit to upper limit, so the integral operator must be shifted according to the lower limit. Accordingly, the function t, which is the value of integral operator, only is shifted to the function t−t0 and it does not mean that the value of operator has varied. _____(5.9). .
In Theorem 1.1 in Chapter 2 Section 1.5, the author showed that the norm of the integral operator is h when the interval is [t, t+h]. If the interval is [t0, t] the following theorem holds. However, it does not mean that the value of integral operator varies. The definition of integral is the integration from lower limit to upper limit, so the integral operator must be shifted according to the lower limit. Accordingly, the function t, which is the value of integral operator, only is shifted to the function t−t0 and it does not mean that the value of operator has varied.
. .
[Theorem 5.1]. .The norm of the integral operator is |t−t0| if the integral interval is from t0 to t.
[Proof]. .Supposing t>t0,
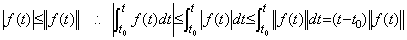 ____(5.10)
In case of t<t0, ____(5.10)
In case of t<t0,
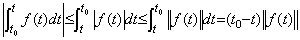 _____(5.11)
All equalities are satisfied if the function f(t) is constant.______________________[Q.E.D.] _____(5.11)
All equalities are satisfied if the function f(t) is constant.______________________[Q.E.D.]
. .
If the n value is not integer and approaches to −1, the coefficient of the linear function in Eq. (5.2) approaches to infinite value. In the case, denoting the function atn by f(t), it is expressed in Taylor's expansion with the remainder as to t0≠0.
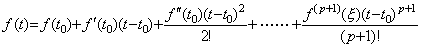 ____(5.12)
The operator value whose integral operator integrates every term of the right side is expressed in the linear equation having the integer from 1 to p+2 on the denominator. Therefore the operator value expressed in Eq. (5.2) may be considered as only the linear equation whose n value is the positive integer or zero. This shows that the n value does not mean that the value of operator is different. ____(5.12)
The operator value whose integral operator integrates every term of the right side is expressed in the linear equation having the integer from 1 to p+2 on the denominator. Therefore the operator value expressed in Eq. (5.2) may be considered as only the linear equation whose n value is the positive integer or zero. This shows that the n value does not mean that the value of operator is different.
. .
The operand of integral in Eq. (5.2) was expressed in atn, (n≠−1) generally, so the operand of the inverse operation, that is, the operand of the differential may be expressed in bt(n+1). In this case, the differential operator and the operator value are expressed in,
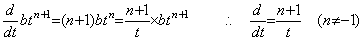 _____(5.13)
The inverse operator of the integral operator with a value n is the differential operator expressed in Eq. (5.13) with the same value n and the product of both becomes always one. In usual, it is said that the product of both operators does not become one when the integral operator is operated after the differential operator. It is caused by grave mistake considering that the integral operator consists of two operations, that is, integration and addition of initial value. It is correct that the integral operator has not the operation adding initial value and obtains y(t)−y0. Accordingly, it is also mistake that the operand of differential operator is y(t) as usual. It must be y(t)−y0. The value of the integral operator is constant value because the n value is no part of the operator value, so the value of the differential operator is also constant value without the n value, which is no part of the operator value, and the function 1/t with n=0. The norm is also the function 1/t but the function |1/t| in order that the product of the norm of the operator and operand does not become negative when t is negative. Accordingly, the product of the norm of both operators also satisfies followings. _____(5.13)
The inverse operator of the integral operator with a value n is the differential operator expressed in Eq. (5.13) with the same value n and the product of both becomes always one. In usual, it is said that the product of both operators does not become one when the integral operator is operated after the differential operator. It is caused by grave mistake considering that the integral operator consists of two operations, that is, integration and addition of initial value. It is correct that the integral operator has not the operation adding initial value and obtains y(t)−y0. Accordingly, it is also mistake that the operand of differential operator is y(t) as usual. It must be y(t)−y0. The value of the integral operator is constant value because the n value is no part of the operator value, so the value of the differential operator is also constant value without the n value, which is no part of the operator value, and the function 1/t with n=0. The norm is also the function 1/t but the function |1/t| in order that the product of the norm of the operator and operand does not become negative when t is negative. Accordingly, the product of the norm of both operators also satisfies followings.
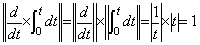 ______(5.14). .
Denoting an operator by T, if T is the integral operator the following is satisfied. ______(5.14). .
Denoting an operator by T, if T is the integral operator the following is satisfied.
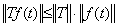 ______(5.15)
However, it is not satisfied in the case that T is the differential operator. Replacing f(t) in Eq. (5.15) with f '(t) and denoting the integral Tf '(t) by f(t)−f0, the relation in Eq. (5.16) is obtained. In usual argument, it may be the reason by which the differential operator has no upper bound but it is mistake. That the differential operator has no upper bound means that the definition of differential exists infinitely. It is in conflict with the fact that the definition does not change. Eq. (5.16) only says that the maximum absolute value of the derivative becomes equal or greater than the product of the norms of differential operator and operand. Even if the norm of the derivative does not exist, the inequality is hold when the norm of f '(t) is replaced with infinity. The usual arguments that the differential operator has no upper bound are mistake. ______(5.15)
However, it is not satisfied in the case that T is the differential operator. Replacing f(t) in Eq. (5.15) with f '(t) and denoting the integral Tf '(t) by f(t)−f0, the relation in Eq. (5.16) is obtained. In usual argument, it may be the reason by which the differential operator has no upper bound but it is mistake. That the differential operator has no upper bound means that the definition of differential exists infinitely. It is in conflict with the fact that the definition does not change. Eq. (5.16) only says that the maximum absolute value of the derivative becomes equal or greater than the product of the norms of differential operator and operand. Even if the norm of the derivative does not exist, the inequality is hold when the norm of f '(t) is replaced with infinity. The usual arguments that the differential operator has no upper bound are mistake.
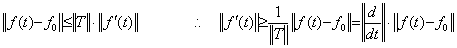 _____(5.16). .
Laplace transform denotes the differential operator by s. It is the derivative of the impulse function δ(t), which is not Dirac's delta function but the impulse function defined in Chapter 2 Section 3.2. The convolution integral becomes, _____(5.16). .
Laplace transform denotes the differential operator by s. It is the derivative of the impulse function δ(t), which is not Dirac's delta function but the impulse function defined in Chapter 2 Section 3.2. The convolution integral becomes,
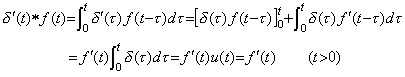 ____(5.17)
In case of the function and derivative denoted by f(t)u(t) and f '(t)u(t), using u(t)=1 and δ(t)=0 in the integrand because the value t is the upper limit of the integration, ____(5.17)
In case of the function and derivative denoted by f(t)u(t) and f '(t)u(t), using u(t)=1 and δ(t)=0 in the integrand because the value t is the upper limit of the integration,
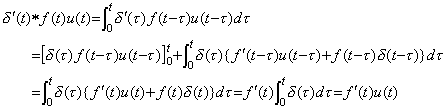 ___(5.18). .
Accordingly, the value of differential operator is δ' (t) even if the operand is any function, that is, it is constant value. Using Theorem 3.7 in Chapter 2 Section 3.9, the product of u(t) and δ' (t), that is, the convolution integral becomes as follows. ___(5.18). .
Accordingly, the value of differential operator is δ' (t) even if the operand is any function, that is, it is constant value. Using Theorem 3.7 in Chapter 2 Section 3.9, the product of u(t) and δ' (t), that is, the convolution integral becomes as follows.
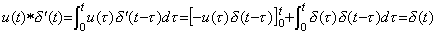 ___(5.19)
The impulse function denotes the identity operation because, ___(5.19)
The impulse function denotes the identity operation because,
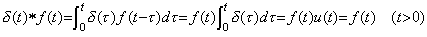 ____(5.20) ____(5.20)
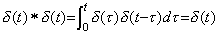 ______(5.21)
Mikusinski denotes it the numerical operator 1. The value of differential operator and the value of identity operator are positive constant values as operator value, because these does not change the sign of u(t) and f(t), whereas δ' (t) varies from +∞ to −∞ at t=+0 as function and δ(t) varies from 0 to +∞ at t=+0 as function. Therefore, ______(5.21)
Mikusinski denotes it the numerical operator 1. The value of differential operator and the value of identity operator are positive constant values as operator value, because these does not change the sign of u(t) and f(t), whereas δ' (t) varies from +∞ to −∞ at t=+0 as function and δ(t) varies from 0 to +∞ at t=+0 as function. Therefore,
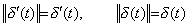 ________(5.22) ________(5.22)
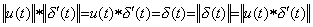 ____(5.23)
Expressing these products as convolution integral in the usual multiplication, the norms of the identity operator and the differential operator become 1 and 1/t respectively as follows. ____(5.23)
Expressing these products as convolution integral in the usual multiplication, the norms of the identity operator and the differential operator become 1 and 1/t respectively as follows.
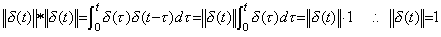 ___(5.24) ___(5.24)
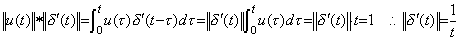 ___(5.25)
The relation as to the product of two operators and as to these norm does not need to satisfy the inequality as Eq. (5.15) and only satisfies the equality, because the value of the operator whose definition is not changed by the function of operand is the constant value that is not changed by the operand and because the norm of operator is also equal to the value of operator. ___(5.25)
The relation as to the product of two operators and as to these norm does not need to satisfy the inequality as Eq. (5.15) and only satisfies the equality, because the value of the operator whose definition is not changed by the function of operand is the constant value that is not changed by the operand and because the norm of operator is also equal to the value of operator.
. .
Denoting an operator by T and expressing a function f(t) in Maclaurin's expansion,
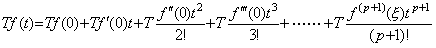 ___(5.26)
If T is the integral operator, the (n+1)th T of the right side is equivalent to t/(n+1) but these T values for n=0, 1, 2, 3, …… are all equivalent as operator value because the distributing law is held. If the function f(t) is changed, it is usually said that the operator value of the left side varies. However, what varies is not the operator value but the coefficients f(n)(0) of Maclaurin's expansion. Accordingly, the operator value is constant value, that is, the function t and the norm also is the function t. ___(5.26)
If T is the integral operator, the (n+1)th T of the right side is equivalent to t/(n+1) but these T values for n=0, 1, 2, 3, …… are all equivalent as operator value because the distributing law is held. If the function f(t) is changed, it is usually said that the operator value of the left side varies. However, what varies is not the operator value but the coefficients f(n)(0) of Maclaurin's expansion. Accordingly, the operator value is constant value, that is, the function t and the norm also is the function t.
. .
If T is the differential operator, the (n+1)th T of the right side is equivalent to n/t but these values are all equivalent as operator value and do not vary even if the function f(t) is changed. Accordingly, the operator value is constant value, that is, the function 1/t and the norm, that is, the metric is also the function 1/t.
. .
It is easy to understand these relations between the operator values and the norm, if we use the concept of vectors. Denoting the function f(t) expressed in Maclaurin's expansion Eq. (5.26) by the vertical vector, which is printed horizontally and denoted by parentheses in order to save space,
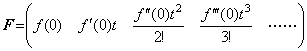 ____(5.27)
If T is the integral operator, Eq. (5.26) is expressed in, ____(5.27)
If T is the integral operator, Eq. (5.26) is expressed in,
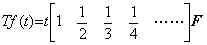 ____(5.28)
If T is the differential operator, Eq. (5.26) is expressed in Eq. (5.29). L_shift denotes the operator that shifts every member of the vector F to left by one column after it has removed f(0) from the vector F expressed in Eq. (5.27). ____(5.28)
If T is the differential operator, Eq. (5.26) is expressed in Eq. (5.29). L_shift denotes the operator that shifts every member of the vector F to left by one column after it has removed f(0) from the vector F expressed in Eq. (5.27).
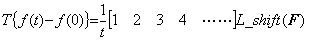 _____(5.29)
These operator values denoted by horizontal vector do not vary even if the operand is changed, that is, the operator values are constant value. If the operand is f(t)=atn, the function with n=0 is the first element of Eq. (5.30), so only the (n+1)th element of the vector F is not zero. _____(5.29)
These operator values denoted by horizontal vector do not vary even if the operand is changed, that is, the operator values are constant value. If the operand is f(t)=atn, the function with n=0 is the first element of Eq. (5.30), so only the (n+1)th element of the vector F is not zero.
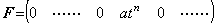 _____(5.30)
Accordingly, multiplying the vector of integral operator and the vector F together, it seems that the integral operator has only the (n+1)th element of Eq. (5.28) as mentioned in Eq. (5.2). This integral result is f(t)−f0, so it is bt(n+1) and Eq. (5.30) has only the (n+2)th element as the element being not zero. By the L_shift operation, only the (n+1)th element is not zero, so it seems that the differential operator as the inverse operation has the (n+1)th element in Eq. (5.29) as expressed in Eq. (5.13). This is the reason that the n value has no meaning as the value of operator. _____(5.30)
Accordingly, multiplying the vector of integral operator and the vector F together, it seems that the integral operator has only the (n+1)th element of Eq. (5.28) as mentioned in Eq. (5.2). This integral result is f(t)−f0, so it is bt(n+1) and Eq. (5.30) has only the (n+2)th element as the element being not zero. By the L_shift operation, only the (n+1)th element is not zero, so it seems that the differential operator as the inverse operation has the (n+1)th element in Eq. (5.29) as expressed in Eq. (5.13). This is the reason that the n value has no meaning as the value of operator.
. .
The norm of the function f(t) is also the function which is denoted by the vector whose first element only is not zero such that,
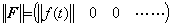 ____(5.31)
Hence, If T is the integral operator, ____(5.31)
Hence, If T is the integral operator,
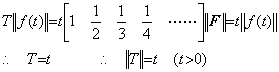 ____(5.32)
Accordingly, the row vector in Eq. (5.28) has no effect on the norm and value of the integral operator. This is the reason that the n value in Eq. (5.2) has no meaning as the norm of operator. Because of |F|≤||F||, ____(5.32)
Accordingly, the row vector in Eq. (5.28) has no effect on the norm and value of the integral operator. This is the reason that the n value in Eq. (5.2) has no meaning as the norm of operator. Because of |F|≤||F||,
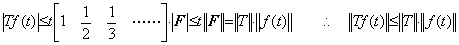 ___(5.33). .
In the case that the operator T is the differential operator, replacing the vector F in Eq. (5.29) with the norm ||F||, it is not able to carry out the operation correspond to Eq. (5.32) by the reason T||F||=0, so it is not able to obtain the norm and value of the differential operator. Also in usual differential operation, the result of differential cannot be obtained because if the operand is the constant function ||f(t)|| the initial value is also ||f(t)|| and the difference of both is zero. The cause that the norm of differential operator is not obtained is that the concept of the norm of function loses all the property needed to obtain the norm of differential result. The norm of differential operator must be obtained by differentiating the integral result T||f(t)|| of the norm of function ||f(t)|| in Eq. (5.32). T||f(t)|| is expressed in Eq. (5.34) as the vector because of a linear function as to t. ___(5.33). .
In the case that the operator T is the differential operator, replacing the vector F in Eq. (5.29) with the norm ||F||, it is not able to carry out the operation correspond to Eq. (5.32) by the reason T||F||=0, so it is not able to obtain the norm and value of the differential operator. Also in usual differential operation, the result of differential cannot be obtained because if the operand is the constant function ||f(t)|| the initial value is also ||f(t)|| and the difference of both is zero. The cause that the norm of differential operator is not obtained is that the concept of the norm of function loses all the property needed to obtain the norm of differential result. The norm of differential operator must be obtained by differentiating the integral result T||f(t)|| of the norm of function ||f(t)|| in Eq. (5.32). T||f(t)|| is expressed in Eq. (5.34) as the vector because of a linear function as to t.
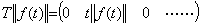 ____(5.34)
Denoting the differential operator in Eq. (5.29) by D and differentiating T||f(t)||, ____(5.34)
Denoting the differential operator in Eq. (5.29) by D and differentiating T||f(t)||,
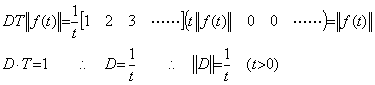 _____(5.35)
Replacing the function of integral operand in Eq. (5.33) by f '(t), _____(5.35)
Replacing the function of integral operand in Eq. (5.33) by f '(t),
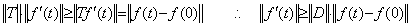 _____(5.36). .
Denoting the integral operator in Eq. (5.28) by the vector T and denoting the differential operator in Eq. (5.29) by the vector D, the product of both operators must be carry out by converting the vector on the right into the column vector. As shown in the explanation of Eq. (5.30), the inverse operation of the integral whose operation uses the (n+1)th element of the vector T uses the (n+1)th element of the vector D, so all the elements of the product of the vectors T and D become 1. It has no difference to change the order of both operators. In usual arguments about integral and differential, it is said that the case of inverse order is not identical operation but it is wrong. As the author said already, so the operand function of differential is f(t)−f(0) and the integral of the derivative f '(t) is also f(t)−f(0). In usual, it is said that the integral result must be the sum of it and f(0).However, it is the compound operation that consist of the integral and adding the initial value, and it is not the integral operation. Also it is mistake that the integral operation has the initial value of result as the operand of integral, because it does not exist in the derivative. The product of both operators is denoted by the vector as the identity operator expressed in Eq. (5.37). _____(5.36). .
Denoting the integral operator in Eq. (5.28) by the vector T and denoting the differential operator in Eq. (5.29) by the vector D, the product of both operators must be carry out by converting the vector on the right into the column vector. As shown in the explanation of Eq. (5.30), the inverse operation of the integral whose operation uses the (n+1)th element of the vector T uses the (n+1)th element of the vector D, so all the elements of the product of the vectors T and D become 1. It has no difference to change the order of both operators. In usual arguments about integral and differential, it is said that the case of inverse order is not identical operation but it is wrong. As the author said already, so the operand function of differential is f(t)−f(0) and the integral of the derivative f '(t) is also f(t)−f(0). In usual, it is said that the integral result must be the sum of it and f(0).However, it is the compound operation that consist of the integral and adding the initial value, and it is not the integral operation. Also it is mistake that the integral operation has the initial value of result as the operand of integral, because it does not exist in the derivative. The product of both operators is denoted by the vector as the identity operator expressed in Eq. (5.37).
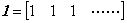 ________(5.37)
The vector of differential operator D and the vector of integral operator T operate on the vector of function F as the row vector, but the right operator must be transformed into the column vector in case of the product of both operators. The cause is due to the result that does not denote the product of the operator and the vector of operand function by the vector of resultant function. Denoting the result by the vector of resultant function, these products are expressed in the matrix equations. It introduces another operational calculus based on Maclaurin's expansion or Taylor's expansion. ________(5.37)
The vector of differential operator D and the vector of integral operator T operate on the vector of function F as the row vector, but the right operator must be transformed into the column vector in case of the product of both operators. The cause is due to the result that does not denote the product of the operator and the vector of operand function by the vector of resultant function. Denoting the result by the vector of resultant function, these products are expressed in the matrix equations. It introduces another operational calculus based on Maclaurin's expansion or Taylor's expansion.
. .
Supposing the function f(t) of Eq. (5.26) is the derivative of y(t), the left side of Eq. (5.26) becomes y(t)−y(0) if T is the integral operator. Expressing the left side in Maclaurin's expansion,
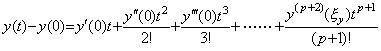 ____(5.38)
Each term of the right side is equal to the respective term of Eq. (5.26). Accordingly, denoting f(t) and y(t)−y(0) by the vectors mentioned in Eq. (5.27), the integral operation is expressed in following matrix equation. ____(5.38)
Each term of the right side is equal to the respective term of Eq. (5.26). Accordingly, denoting f(t) and y(t)−y(0) by the vectors mentioned in Eq. (5.27), the integral operation is expressed in following matrix equation.
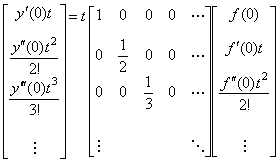 _____(5.39)
In a similar way, the differential operation is expressed in, _____(5.39)
In a similar way, the differential operation is expressed in,
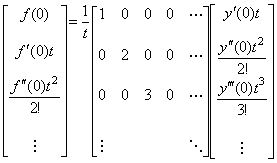 _____(5.40)
The product of the two operators becomes the unit matrix, that is, the identity operator. _____(5.40)
The product of the two operators becomes the unit matrix, that is, the identity operator.
. .
Successively differentiating the product of two functions f(t) and g(t),
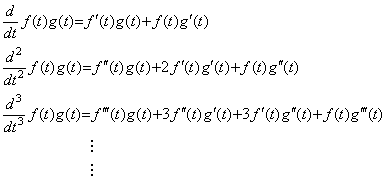 ____(5.41)
Accordingly, expressing Maclaurin's expansion of the product f(t)g(t) in the product of Maclaurin's expansions of f(t) and g(t), the product of the two vectors expressed in matrix equation. ____(5.41)
Accordingly, expressing Maclaurin's expansion of the product f(t)g(t) in the product of Maclaurin's expansions of f(t) and g(t), the product of the two vectors expressed in matrix equation.
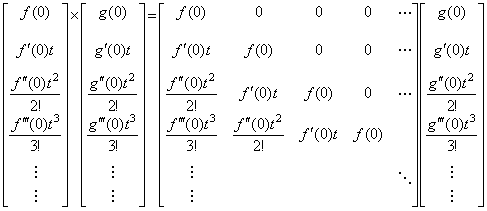 ___(5.42)
The matrix is the operator equivalent to the vector and the author names it the expansion of vector into the matrix, that is, the operator. The product of two vectors must be carried out with expanding the left vector into the operator. However, the expansion has no change as to the norm and other properties except for the form of expression, as same as the integer number is transformed into the real number by appending decimal point. This is the definition of multiplication of two vectors, as Laplace transform and Mikusinski's operational calculus define the product of two functions by the convolution integral. Accordingly, the product of the differential or integral operator and the vector also must be carried out with expanding the differential or integral operator into the matrix. The integral operator is the function t and the expansion into the matrix is expressed in the integral operator of Eq. (5.39). The differential operator is the function 1/t and the expansion into the matrix is expressed in the differential operator of Eq. (5.40). These matrixes into which the operator is expanded have no effect on the norm. The elements of both operators are all zero except the diagonal elements and all the diagonal elements are not same value, so these operators differ from the matrixes into which the vector is expanded. The matrixes of the differential and integral operators in the author's operational calculus based on successive differences are the same as these. ___(5.42)
The matrix is the operator equivalent to the vector and the author names it the expansion of vector into the matrix, that is, the operator. The product of two vectors must be carried out with expanding the left vector into the operator. However, the expansion has no change as to the norm and other properties except for the form of expression, as same as the integer number is transformed into the real number by appending decimal point. This is the definition of multiplication of two vectors, as Laplace transform and Mikusinski's operational calculus define the product of two functions by the convolution integral. Accordingly, the product of the differential or integral operator and the vector also must be carried out with expanding the differential or integral operator into the matrix. The integral operator is the function t and the expansion into the matrix is expressed in the integral operator of Eq. (5.39). The differential operator is the function 1/t and the expansion into the matrix is expressed in the differential operator of Eq. (5.40). These matrixes into which the operator is expanded have no effect on the norm. The elements of both operators are all zero except the diagonal elements and all the diagonal elements are not same value, so these operators differ from the matrixes into which the vector is expanded. The matrixes of the differential and integral operators in the author's operational calculus based on successive differences are the same as these.
5.3 The definition of the norm of operators in usual differential and integral.
. .
It may be thought that the integration of the integrand at n, (n≠−1) expressed in Eq. (5.2) is based on the mean value theorem. Supposing ξ is the point at which the value of integrand is equal to the mean value of integral from 0 to t, the integral from 0 to t becomes aξ nt, because the mean value of integral is aξ n. The value ξ n is 1 for n=0, midpoint t/2 for n=1 and for other case of n it is expressed in Eq. (5.43). Accordingly, the linear function whose denominator has n+1 in Eq. (5.2) is the product of the function t and the operator transforming the integrand into the mean value of integral from 0 to t.
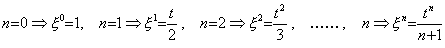 _______(5.43). .
It seams that this operator transforming the integrand into the mean value changes the value by changing the order n of the integrand. However, by the reason that the integral holds the distributing law in Maclaurin's expansion of Eq. (5.26), it must be considered that these operators with n value are all equal. It must be considered that the value of the transforming operator is 1, because the n value is unrelated to the value of operator. Therefore, the value of integral operator is the function t. _______(5.43). .
It seams that this operator transforming the integrand into the mean value changes the value by changing the order n of the integrand. However, by the reason that the integral holds the distributing law in Maclaurin's expansion of Eq. (5.26), it must be considered that these operators with n value are all equal. It must be considered that the value of the transforming operator is 1, because the n value is unrelated to the value of operator. Therefore, the value of integral operator is the function t.
. .
Introducing the idea of the vector expressed in brackets of Eq. (5.28), this operator transforming the integrand into the mean value is considered as the set whose members are all the values calculated by 1/(n+1) and whose one member corresponding to the n value of the integrand at n, (n≠−1) operates on the integrand. The set exists only one, so the integral operators T in the right side of Eq. (5.26) are all equal and the distributing law is held. Furthermore, the integral operators T in the left side and in the right side are the same even if the n value is any, so the value of the set as the operator must be 1, that is, the value of member for n=0 and the norm is also 1. Therefore, the value of integral operator is the function t and the norm is also the function t.
. .
The integral of the function at n, (n≠−1) may be denoted by bt(n+1). The inverse operation, that is, the differential is expressed in Eq. (5.13). It may be considered that the inverse operation transforms the mean value aξ n into the function at n by multiplying n+1 after the mean value was obtained by the product of 1/t and the function of operand, because the integral is the product of t and the mean value of the integrand. The results (n+1)ξ n for the n value are expressed in Eq. (5.44) from Eq. (5.43). Therefore, the numerator n+1 of the differential operator in Eq. (5.13) is the operator transforming the mean value into the function.
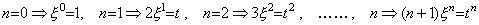 _________(5.44). .
This operator transforming the mean value into the function is the set whose members are all the values calculated by n+1 and whose one member operates on the mean value, corresponding with the n value of the operand bt(n+1). This is the reason by which the differential in Maclaurin's expansion, that is, the operator T in Eq. (5.26) holds the distributing law as the differential operator. The value of the operator transforming the mean value into the function must be 1 as the value of set and the norm also is 1. Therefore, it has no effect on the value of differential operator, so the value of differential operator is the function 1/t and the norm also is the function 1/t. _________(5.44). .
This operator transforming the mean value into the function is the set whose members are all the values calculated by n+1 and whose one member operates on the mean value, corresponding with the n value of the operand bt(n+1). This is the reason by which the differential in Maclaurin's expansion, that is, the operator T in Eq. (5.26) holds the distributing law as the differential operator. The value of the operator transforming the mean value into the function must be 1 as the value of set and the norm also is 1. Therefore, it has no effect on the value of differential operator, so the value of differential operator is the function 1/t and the norm also is the function 1/t.
. .
That the operator transforming the function into the mean value and the inverse operator transforming the mean value into the function have the value 1 and the norm 1 denotes that both operators are the identity operator and that these have no effect on the property of the operand as same as the expansion of vector into the matrix expressed in Eq. (5.42). The members corresponding the same value n of both sets are reciprocal number, so it may be considered that there exists only the set whose member transforms the function into the mean value and that the reciprocal number of the member operates on the operand in the case of the differential. The matrixes in Eq. (5.39) and Eq. (5.40), which denote the differential and integral of Maclaurin's expansion by the matrix expression, also have the same meaning as these. The matrixes that is the differential and integral operators of the author's operational calculus also have the same meaning as these.
. .
[Definition 5.1]. .Supposing the point ξ t is the point at which the value of f(t) is equivalent to the mean value of integral of f(t) from t=0 to arbitrary t, the mean value is denoted by the function f(ξ t). The author names the function the mean function of f(t).
. .
The author expands the arguments mentioned above into the differential and integral of general functions. Denoting the derivative of the function y(t) by f(t), the integral operation is expressed in the mean function f(ξ t) as follows.
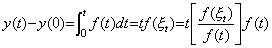 _____(5.45)
What is denoted by use of the brackets is the operator transforming the function into the mean value. This operator is the set whose members are all the ordered pairs of the integrable function f(t) and the mean function f(ξ t), and the member whose integrable function is equal to the integrand f(t) operates on the integrand with the mean function according to Eq. (5.45). In the case of Eq. (5.43), the integrand is at n and the mean function is at n/(n+1), so the value of the ordered pair transforming the integrand into the mean function is 1/(n+1). In the case, the norm of the operator, that is, the set is the value 1 that is given by the ordered pair whose integrand and mean function are equivalent. In the same way, the norm of the operator, that is, the set transforming the general function into the mean function in Eq. (5.45) is the value 1 that is given by the ordered pair whose integrand f(t) and mean function f(ξ t) are equivalent. This operator exists only one and the norm is 1, so the value of operator is 1. Accordingly, the integrand f(t) and the mean function f(ξ t) are equivalent. Therefore, the value of integral operator is the function t and the norm also is the function t. _____(5.45)
What is denoted by use of the brackets is the operator transforming the function into the mean value. This operator is the set whose members are all the ordered pairs of the integrable function f(t) and the mean function f(ξ t), and the member whose integrable function is equal to the integrand f(t) operates on the integrand with the mean function according to Eq. (5.45). In the case of Eq. (5.43), the integrand is at n and the mean function is at n/(n+1), so the value of the ordered pair transforming the integrand into the mean function is 1/(n+1). In the case, the norm of the operator, that is, the set is the value 1 that is given by the ordered pair whose integrand and mean function are equivalent. In the same way, the norm of the operator, that is, the set transforming the general function into the mean function in Eq. (5.45) is the value 1 that is given by the ordered pair whose integrand f(t) and mean function f(ξ t) are equivalent. This operator exists only one and the norm is 1, so the value of operator is 1. Accordingly, the integrand f(t) and the mean function f(ξ t) are equivalent. Therefore, the value of integral operator is the function t and the norm also is the function t.
. .
[Definition 5.2]. .The author names the set whose members are all the ordered pairs of the integrable function f(t) and the mean function f(ξ t) the transform operator into the mean function. When this operator operates on the integrand, the member whose ordered pair has the function f(t) equal to the integrand operates on the integrand as the fraction whose denominator is the function f(t) and whose numerator is the mean function f(ξ t).
. .
The differential of arbitrary function y(t) is denoted as follows from Eq. (5.45).
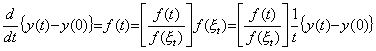 _____(5.46)
Accordingly, in the case of the differential, the member of the transform operator into the mean function operates reciprocally on the mean function f(ξ t), that is, the mean of differential {y(t)−y(0)}/t as the fraction whose denominator is the function f(ξ t) equal to the mean of differential and whose numerator is the function f(t), that is, other part of the pair. Hence, this operator is the operator transforming the mean function f(ξ t) into the function f(t) and it is the inverse operator of the transform operator into the mean function. The value and norm of this inverse operator are 1, because the value and norm of the transform operator into the mean function are 1. Therefore, the value and norm of differential operator are 1/t. _____(5.46)
Accordingly, in the case of the differential, the member of the transform operator into the mean function operates reciprocally on the mean function f(ξ t), that is, the mean of differential {y(t)−y(0)}/t as the fraction whose denominator is the function f(ξ t) equal to the mean of differential and whose numerator is the function f(t), that is, other part of the pair. Hence, this operator is the operator transforming the mean function f(ξ t) into the function f(t) and it is the inverse operator of the transform operator into the mean function. The value and norm of this inverse operator are 1, because the value and norm of the transform operator into the mean function are 1. Therefore, the value and norm of differential operator are 1/t.
. .
[Definition 5.3]. .
In the case of the differential, the member of the transform operator into the mean function operates reciprocally on the mean function f(ξ t), that is, the mean of differential {y(t)−y(0)}/t as the fraction whose denominator is the function f(ξ t) equal to the mean of differential and whose numerator is the function f(t), that is, other part of the pair.
. .
The cause by which these operators must be appended to the differential and integral operators is due to the abstract argument that treats the differential and integral as the multiplication of the abstractly linear operator and the function. Laplace transform and Mikusinski's operational calculus define the multiplication of two functions as the convolution integral, so these can realize to carry out the differential and integral by multiplication of the operator and the operand. The usual integral can be carried out by multiplication of the integral operator and the integrand only in the case that the integrand is a constant function and the usual differential can be carried out by multiplication of the differential operator and the operand only in the case that the operand is a linear function. In the case that the operand is arbitrary function, the integral needs the operator transforming the integrand into the mean function and the differential needs the inverse operator, that is, the operator transforming the mean function of the differential into the function. These transforming operators are what operate on the function of operand and not what operate on the differential and integral operators. It is possible to define the multiplication of the differential or integral operator and the function of operand by these transforming operators as same as Laplace transform and Miksinski's operational calculus. The multiplication operator has no value but even if it has a value, the value must be 1 and the norm must be 1.
. .
[Definition 5.4]. .Denoting the transform operator into the mean function by the symbol *, the author defines the multiplication of the integral operator and the integrand by the symbol. Accordingly, the integral is expressed in Eq. (5.47) and the differential is expressed in Eq. (5.48), where the inverse operator *−1 operates on the operand multiplied by the operator 1/t.
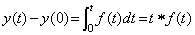 _______(5.47) _______(5.47)
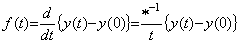 ____(5.48) ____(5.48)
. .
In usual, it is said that the differential operator is not bounded upwards but it has no meaning because it is based on the abstract argument that is not realizable. The following example is often shown as the reason by which the differential operator is not bounded upwards. The function y(t) in Eq. (5.49) converges on zero because the norm converges on zero but the derivative of the function y(t) does not converge on zero because the norm converges on 1 as shown in Eq. (5.50). It is said that the cause is that the differential operator is not bounded upwards.
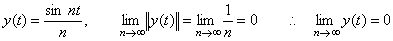 _____(5.49) _____(5.49)
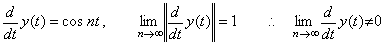 _____(5.50). .
Denoting the linear operator by T, the case of Ty(t)=0 is only the case when the function is y(t)=0. Accordingly, if lim y(t)=0 is held, the equation lim Ty(t)=Tlim y(t)=0 must be held. Eq. (5.50) says that the differential operator and the lim operator cannot change the order of operation because the differential operator is not bounded upwards. However, this argument makes a serious mistake. Speaking the conclusion, the order of the differential operator and the lim operator must be changed. In order to differentiate the function y(t) in Eq. (5.49), the variable t is transformed into the variable f as shown in Eq. (5.51). Here, if the differential by the variable f is carried out, the result becomes Eq. (5.50). However, this differentiation is impossible because of df→∞ for n→∞. Obtaining it simply as the fraction of numerator and denominator, the limit of the differential of y(t) in Eq. (5.49) becomes zero expressed in Eq. (5.51). _____(5.50). .
Denoting the linear operator by T, the case of Ty(t)=0 is only the case when the function is y(t)=0. Accordingly, if lim y(t)=0 is held, the equation lim Ty(t)=Tlim y(t)=0 must be held. Eq. (5.50) says that the differential operator and the lim operator cannot change the order of operation because the differential operator is not bounded upwards. However, this argument makes a serious mistake. Speaking the conclusion, the order of the differential operator and the lim operator must be changed. In order to differentiate the function y(t) in Eq. (5.49), the variable t is transformed into the variable f as shown in Eq. (5.51). Here, if the differential by the variable f is carried out, the result becomes Eq. (5.50). However, this differentiation is impossible because of df→∞ for n→∞. Obtaining it simply as the fraction of numerator and denominator, the limit of the differential of y(t) in Eq. (5.49) becomes zero expressed in Eq. (5.51).
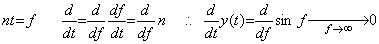 _____(5.51). .
Differentiating the function y(t) by the definition of differential, the differential converges on cos nt for h→0 if the n value is finite. However, nh→0 is needed for n→∞ but it is not held. Eq. (5.50) has carried out h→0 first, supposing the n value is finite. This is wrong because it is equivalent to conclude that nh→0 is held. If the n value has been carried out n→∞ first, the limit of Eq. (5.52) is zero. _____(5.51). .
Differentiating the function y(t) by the definition of differential, the differential converges on cos nt for h→0 if the n value is finite. However, nh→0 is needed for n→∞ but it is not held. Eq. (5.50) has carried out h→0 first, supposing the n value is finite. This is wrong because it is equivalent to conclude that nh→0 is held. If the n value has been carried out n→∞ first, the limit of Eq. (5.52) is zero.
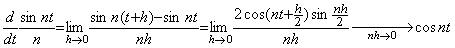 _____(5.52). .
Differentiating the function y(t) by use of the transform operator into the mean function in the definition 5.4, if the n value is finite the mean function becomes cos ξ and the function whose mean function is cos ξ is cos nt. However, the n value is n→∞ the mean function is identical with zero, so the function that has the mean function is also identical with zero. Hence, in Eq. (5.50), the order of the differential operator and the lim operator must be changed. Accordingly, it is concluded that the differential operator is bounded upwards. _____(5.52). .
Differentiating the function y(t) by use of the transform operator into the mean function in the definition 5.4, if the n value is finite the mean function becomes cos ξ and the function whose mean function is cos ξ is cos nt. However, the n value is n→∞ the mean function is identical with zero, so the function that has the mean function is also identical with zero. Hence, in Eq. (5.50), the order of the differential operator and the lim operator must be changed. Accordingly, it is concluded that the differential operator is bounded upwards.
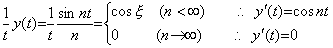 ____(5.53). .
The function y(t) in Eq. (5.54) is also given as the example showing that the differential operator is not bounded upwards. The function y(t) is bounded upwards but the derivative f(t) becomes infinite by t→0, so it is not bounded upwards. It is said that the cause is due to the differential operator that is not bounded upwards. This argument also is very wrong. Although the derivative f(t) becomes infinite by t→0, there always exists the mean value f(ξ) of integral of the interval [0, t] and it is larger than the value of the function f(t). The mean value f(ξ) of integral is bounded upwards because it becomes the function y(t) by multiplying it by t. Accordingly, the derivative f(t) is bounded upwards and the differential operator also is bounded upwards. ____(5.53). .
The function y(t) in Eq. (5.54) is also given as the example showing that the differential operator is not bounded upwards. The function y(t) is bounded upwards but the derivative f(t) becomes infinite by t→0, so it is not bounded upwards. It is said that the cause is due to the differential operator that is not bounded upwards. This argument also is very wrong. Although the derivative f(t) becomes infinite by t→0, there always exists the mean value f(ξ) of integral of the interval [0, t] and it is larger than the value of the function f(t). The mean value f(ξ) of integral is bounded upwards because it becomes the function y(t) by multiplying it by t. Accordingly, the derivative f(t) is bounded upwards and the differential operator also is bounded upwards.
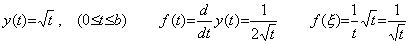 ____(5.54). .
The unite step function u(t) that is often used by Laplace transform is bounded upwards because the norm is 1, but the derivative of u(t) becomes the impulse function δ(t), which the author defined in the 2nd chapter 3.2 sector, and it becomes δ(t)→∞ for t→0. However, the impulse function δ(t) has a peak at this point because the derivative of δ(t) is δ'(t)=0 at this point. Accordingly, there certainly exists finite value larger than the peak and the impulse function is bounded upwards. These examples denote that it is not possible to conclude that the function is not bounded upwards only because the function approaches to infinity. The impulse function δ(t) has very large finite value approximated as δ(+0)=∞ at one point and has zero for all the other points. It is very overestimation to define the norm by the value δ(+0). It is necessary and sufficient to define the norm of the impulse function δ(t) by δ(t) mentioned in the preceding section. The derivative δ'(t) and the unit step function u(t) is also the same as this. The norm of the function that is the operator value is also defined as follows. ____(5.54). .
The unite step function u(t) that is often used by Laplace transform is bounded upwards because the norm is 1, but the derivative of u(t) becomes the impulse function δ(t), which the author defined in the 2nd chapter 3.2 sector, and it becomes δ(t)→∞ for t→0. However, the impulse function δ(t) has a peak at this point because the derivative of δ(t) is δ'(t)=0 at this point. Accordingly, there certainly exists finite value larger than the peak and the impulse function is bounded upwards. These examples denote that it is not possible to conclude that the function is not bounded upwards only because the function approaches to infinity. The impulse function δ(t) has very large finite value approximated as δ(+0)=∞ at one point and has zero for all the other points. It is very overestimation to define the norm by the value δ(+0). It is necessary and sufficient to define the norm of the impulse function δ(t) by δ(t) mentioned in the preceding section. The derivative δ'(t) and the unit step function u(t) is also the same as this. The norm of the function that is the operator value is also defined as follows.
. .
[Definition 5.5]. .
The function as the value of the operator that operates on any operand by the same definition is only one, so the norm is also the function. However, if it changes the sign of operand the norm of operator is the absolute function.
. .
The value of the function f(t) at t=x is the impulse function whose peak is f(x) at this point and expressed in the integrand of the left side of Eq. (5.55). The sum total of these impulse functions for −∞<x<∞, that is, the integral by x is the function f(t). This integral is the convolution integral of the function f(t) and the impulse function, which is the identity operator, so it is evident that the integral becomes f(t). The norm of the function f(t) is the size that the set of these impulse functions denotes. The impulse function whose peak is the maximum absolute value of the function f(t) has equal or lager peak than the absolute peak of any impulse function of the set. However, the impulse function is zero for all the points except for the peak point and smaller than the absolute impulse functions at those points, so it cannot be said that the impulse function denotes the size of the set. The set whose all members are the impulse functions with the maximum absolute peak denotes the size of set, that is, the norm. The sum total of those impulse functions as same as Eq. (5.55) becomes the constant function whose value is the maximum absolute value of the function f(t). Therefore, the norm of the function f(t) is defined by the maximum absolute value.
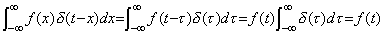 _____(5.55). .
It is said that though the function y(t) in Eq. (5.54) is a continuous function the derivative f(t) is a discontinuous function and that the cause is due to the differential operator being not bounded upwards. Differentiating y(t) by the definition of differential, it is expressed in Eq. (5.56). Accordingly, the value at t=0 is the mean value of f(t) as the integral and the derivative f(t) is not defined at t=0. Because the value of y(t) at t=0 is zero, the mean value of f(t) as the integral is bounded upwards whereas it is infinite, and the mean value multiplied by zero is the initial value y(0)=0. However, it is contradictory that the mean value of integral is defined by the derivative f(ξ) whereas the derivative f(t) is not defined at t=0. Accordingly, the function y(t) cannot be defined at t=0, so it is a discontinuous function. In usual, we are considering that the function y(t) is defined at t=0 because the square root of zero is zero. However, it is wrong. _____(5.55). .
It is said that though the function y(t) in Eq. (5.54) is a continuous function the derivative f(t) is a discontinuous function and that the cause is due to the differential operator being not bounded upwards. Differentiating y(t) by the definition of differential, it is expressed in Eq. (5.56). Accordingly, the value at t=0 is the mean value of f(t) as the integral and the derivative f(t) is not defined at t=0. Because the value of y(t) at t=0 is zero, the mean value of f(t) as the integral is bounded upwards whereas it is infinite, and the mean value multiplied by zero is the initial value y(0)=0. However, it is contradictory that the mean value of integral is defined by the derivative f(ξ) whereas the derivative f(t) is not defined at t=0. Accordingly, the function y(t) cannot be defined at t=0, so it is a discontinuous function. In usual, we are considering that the function y(t) is defined at t=0 because the square root of zero is zero. However, it is wrong.
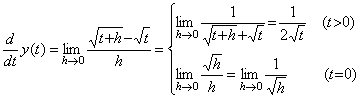 _____(5.56). .
If the function y(t) is not defined at t=0, it may be considered that a trouble is caused for the definition that the operand of differential is the function subtracted the initial value. However, considering the interval [ε, t], both of the differential and the integral has no trouble as follows, but the view about the continuously differentiable function must be changed. _____(5.56). .
If the function y(t) is not defined at t=0, it may be considered that a trouble is caused for the definition that the operand of differential is the function subtracted the initial value. However, considering the interval [ε, t], both of the differential and the integral has no trouble as follows, but the view about the continuously differentiable function must be changed.
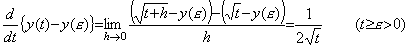 _____(5.57). . _____(5.57). .
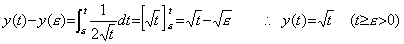 ________(5.58). .
In usual, it is said that there is the relations expressed in Eq. (5.59) as to the space of the continuously differentiable functions. This argument also is a one-sided argument considering only the case of the differential and no considering the case of the integral because of the trouble for the view that the differential operator is not bounded upwards. ________(5.58). .
In usual, it is said that there is the relations expressed in Eq. (5.59) as to the space of the continuously differentiable functions. This argument also is a one-sided argument considering only the case of the differential and no considering the case of the integral because of the trouble for the view that the differential operator is not bounded upwards.
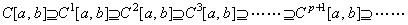 ______(5.59) ______(5.59)
. .
[Theorem 5.2]_____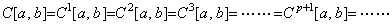 _______(5.60) _______(5.60)
[Proof]. .Supposing the continuously differentiable functions consist of the functions that are continuous after differentiation and the functions that are not continuous after differentiation, the relations in Eq. (5.59) are satisfied. On the other hand, integrating every function on C[a, b] with a proper constant of integral, all these functions are the once continuously differentiable functions. Furthermore, all the results with other proper constant of integral are the once continuously differentiable functions. Therefore, the relation C[a, b]⊆C1[a, b] is satisfied. Integrating the functions on C1[a, b] as the same way, all the results become the twice continuously differentiable functions and the relation C1[a, b]⊆C2[a, b] is satisfied. In the same way, the relations in Eq. (5.61) are satisfied. Therefore, the relations in Eq (5.60) are held.
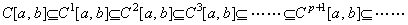 _____(5.61)____[Q.E.D.] _____(5.61)____[Q.E.D.]
. .
This theorem shows that the continuous function is limitless times continuously differentiable. The linear function becomes identical zero by twice differentiation and the function of identical zero becomes identical zero by differentiation, so it is limitless times continuously differentiable. The function y(t) in Eq. (5.54) cannot define the derivative that is the property of function at t=0 as shown in Eq. (5.56). Usual consideration that the function nevertheless is defined at the point is not proper. The value of function at this point is not defined, that is, the function is discontinuous function, so the derivative is discontinuous function and it is not that the continuous function has become discontinuous by differentiation. The trouble of usual definition about continuous functions is mentioned in following sector.
5.4 The trouble of usual definition about continuous functions.
. .
Considering only that the function y(t) in Eq. (5.54) is the square root of t, the value of function is y(t)=0 at t=0, so it seems the function continuous for t≥0. In usual, it is considered so. However, considering the differential coefficient, this consideration is not proper as mentioned in the preceding section. The mathematical small dictionary edited by Kentaro Yano defines the continuous function as follows by two ways, omitting a partial description.
. .
[Continuous function]. .When the function f(x) whose values are real numbers and defined on an open interval of real number satisfies the condition in Eq. (5.62) at a point a on the interval, the function f(x) is continuous at x=a. If the function is continuous at all the points on the open interval, the function is continuous on the open interval. ……
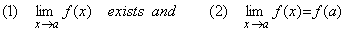 ______(5.62)
…… That the function f(x) is continuous at x=a also may be said as follows. Supposing any positive real number ε and selecting a proper positive real number δ depending on ε, if it is possible to hold |f(x)−f(a)|<ε for all the x value satisfying |x−a|<δ, the function f(x) is continuous at x=a. ______(5.62)
…… That the function f(x) is continuous at x=a also may be said as follows. Supposing any positive real number ε and selecting a proper positive real number δ depending on ε, if it is possible to hold |f(x)−f(a)|<ε for all the x value satisfying |x−a|<δ, the function f(x) is continuous at x=a.
. .
The first half of this definition and the latter half of it are not equivalent. According to the condition (5.62) of the first half of the definition, the function y(t) in Eq. (5.54) is continuous at t=0 but it is discontinuous according to the latter half of the definition. As shown in Eq. (5.63), denoting the ratio of |f(x)-f(a)| to |x-a|, that is, the absolute mean value of differential by k, the maximum value of kδ must be ε. The k value varies depending on the x value and it becomes the absolute differential coefficient at x=a, so if the differential coefficient does not exist, the condition of the latter half of the definition is not satisfied. Therefore, the differential coefficient must exist at x=a in order that the function is continuous. The first half of the definition has lost this condition.
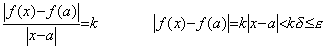 ______(5.63) ______(5.63)
. .
The function y(t) in Eq. (5.54) denotes the square root of t, so it satisfies y(t)→0 for t→0. However, the distance y(t) from 0 is increasing gradually to infinity for the distance t from 0 because the derivative becomes y'(0)=∞. This shows that the speed of y(t) approaching zero gradually becomes slowly and that the speed of y(t) becoming 0 from y(+0) becomes zero. It results in that the function y(t) cannot become zero for t=0. Accordingly, it is right that the condition (2) in Eq. (5.62) is not satisfied. The usual thinking that zero is the square root of zero is mistake and the square root of zero does not exist. The square root of t is defined by y(t)×y(t)=t so it satisfies y(t)=t/y(t) for t>0 but the case of t=0 satisfies 0×0=0 but does not satisfy 0=0/0. The solution of linear equation 0×x=0 is not x=0. The reason why x=0 is the solution of quadratic equation x2=0 is that the product of two equal values becomes zero only in its case. The reason is not that the square root of zero is zero because x=0/x is not permitted. The value 0 does not satisfy the condition of square root of 0.
. .
[Theorem 5.3]. .If the function f(t) is a continuous function, the indefinite integral is a continuous function.
[Proof]. .Denoting arbitrary continuous function by f(t) and integrating it with arbitrary integral constant C, the function y(t) is expressed in the indefinite integral as shown in Eq. (5.64).
 _______(5.64)
The function y(t) satisfies the condition in Eq. (5.62) at arbitrary t=a as shown in the first equation of Eq. (5.65). It also satisfies the condition (5.63) as shown in the second equation of Eq. (5.65). _______(5.64)
The function y(t) satisfies the condition in Eq. (5.62) at arbitrary t=a as shown in the first equation of Eq. (5.65). It also satisfies the condition (5.63) as shown in the second equation of Eq. (5.65).
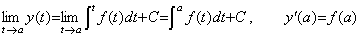 ______(5.65)_____[Q.E.D.] ______(5.65)_____[Q.E.D.]
. .
This theorem supplements Eq. (5.61), that is, the latter half of the proof for the theorem 5.2 in the preceding section. Expressing this in the inverse operation, if the derivative f(t) is continuous function the operand y(t) of differential is continuous function, and if the operand y(t) of differential is not continuous function the derivative f(t) is not continuous function.
. .
[Theorem 5.4]. .If the derivative f(t) is not continuous function the operand y(t) of differential is not continuous function, that is, if the operand y(t) of differential is continuous function the derivative f(t) is continuous function.
[Proof]. .The function y(t) is continuous function, so it becomes y(t+h)→y(t) at arbitrary t and the differential coefficient y'(t) exists by the latter half of above definition about the continuous function. Considering the pair (y(t), y'(t)), the convergence (y(t+h), y'(t+h))→(y(t), y'(t)) is satisfied for h→0, so the derivative f(t)=y'(t) satisfies the condition of continuous (5.62). Accordingly, supposing that k1 and k2 are the maximum absolute mean values of differential on each interval [t−h, t] and [t, t+h] for arbitrary h, it is able to satisfy Eq. (5.66) for all the h value such as h<δ by selecting proper positive value δ according to arbitrary positive value ε.
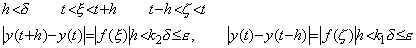 _______(5.66)
Hence, in order that the condition Eq. (5.67) by which the function f(t) is continuous is satisfied for all the values of |ξ−t| and |ζ−t| smaller than h, it is sufficient that the δ value is given such value that kδ≤ε is satisfied, denoting the maximum of k1, k2, 2k3 by k. _______(5.66)
Hence, in order that the condition Eq. (5.67) by which the function f(t) is continuous is satisfied for all the values of |ξ−t| and |ζ−t| smaller than h, it is sufficient that the δ value is given such value that kδ≤ε is satisfied, denoting the maximum of k1, k2, 2k3 by k.
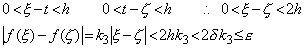 ______(5.67)
ξ→t and ζ→t are satisfied for h→0, so the function f(t) is continuous at arbitrary t. ______(5.67)
ξ→t and ζ→t are satisfied for h→0, so the function f(t) is continuous at arbitrary t.
___________[Q.E.D.]
. .
Above two theorems give another proof for the theorem 5.2, which says in the previous section that the spaces of the continuous function and the continuously differentiable function are identical space. In usual, it is said that the function that is joining two different functions together is continuous function but it is not correct. The function y(t), which consist of two different function joined at t=1 and expressed in (A) of Eq. (5.68), satisfies the condition in Eq. (5.62) at the joining point too, so it is said that the function is continuous function. However, the derivative of y(t) becomes the function f(t) in (B) of Eq. (5.68) and it is discontinuous because it becomes f(t−0)=2, f(t)=1 at the joining point. Accordingly, the function y(t) expressed in (A) also is discontinuous function, that is, the function joined with different differential coefficients is discontinuous function.
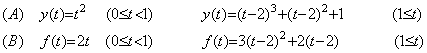 ____(5.68). .
Integrating the function in (A) of Eq. (5.68) with the integral constant C given various values, the functions expressed in Eq. (5.69) are obtained. All these functions are joined smoothly at t=1 with the differential coefficient 1, so these satisfy the continuous condition in Eq. (5.63). However, these functions are discontinuous functions even if these satisfy the continuous condition Eq. (5.63), because the derivative (A) of Eq. (5.68) is discontinuous function. Changing a different constant D for the constant C of one or the other interval, the function is obviously discontinuous function because the values of functions on every interval are different at t=1. In spite of the fact, the derivative becomes (A) of Eq. (5.68). It is contradictory that the derivative of the discontinuous function is the same continuous function as the derivative of continuous function. In this meaning too, the function in Eq. (5.69) is discontinuous function, furthermore the function joined two or more functions is discontinuous function even if the each function is joined with the equal differential coefficients at both sides of joining points. ____(5.68). .
Integrating the function in (A) of Eq. (5.68) with the integral constant C given various values, the functions expressed in Eq. (5.69) are obtained. All these functions are joined smoothly at t=1 with the differential coefficient 1, so these satisfy the continuous condition in Eq. (5.63). However, these functions are discontinuous functions even if these satisfy the continuous condition Eq. (5.63), because the derivative (A) of Eq. (5.68) is discontinuous function. Changing a different constant D for the constant C of one or the other interval, the function is obviously discontinuous function because the values of functions on every interval are different at t=1. In spite of the fact, the derivative becomes (A) of Eq. (5.68). It is contradictory that the derivative of the discontinuous function is the same continuous function as the derivative of continuous function. In this meaning too, the function in Eq. (5.69) is discontinuous function, furthermore the function joined two or more functions is discontinuous function even if the each function is joined with the equal differential coefficients at both sides of joining points.
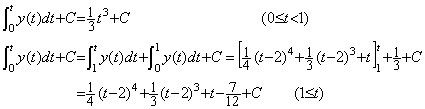 ____(5.69). .
In usual, it is said that such function as is mentioned above with one independent variable exists on the two dimensional space. In practice, the function on the three dimensional space is projected on the two dimensional space as mentioned in the section one, so above mentioned strange phenomena are seen. The origin (0, 0) of the two dimensional space on which the relation between the independent variable t and the value of function y is represented has the third axis orthogonal to the space and the axis represents the value of the constant term of y(t). The author names the coordinate axis the constant axis. The function of the interval (0≤t<1) in Eq. (5.69) exists on the two dimensional space that is orthogonal to the axis at the C point of the constant axis. The function of the interval (1≤t) exists on the two dimensional space that is orthogonal to the axis at the point y(0)=C+3/4 of the constant axis. Accordingly, the function in Eq. (5.69) is not joined on this three dimensional space. The cause that the differential is independent of constant term is that the differential is the operation obtaining the partial differential of the function y(t) as to t-axis and that it is independent of the differential as to the constant axis. It is same meaning also that the constant term is subtracted from the operand of the differential. The result of differential is moved to the two dimensional space that exists at the point denoting the constant term of the derivative. Inversely, the integral operation must decide the position of the two dimensional space on which the resultant function exists, so it needs the constant of integral. Usual argument look at the two dimensional space on which all the two dimensional spaces on the three dimensional space are projected at the origin of the constant axis, so the functions in (A) of Eq. (5.68) and in Eq. (5.69) seems to be joined. ____(5.69). .
In usual, it is said that such function as is mentioned above with one independent variable exists on the two dimensional space. In practice, the function on the three dimensional space is projected on the two dimensional space as mentioned in the section one, so above mentioned strange phenomena are seen. The origin (0, 0) of the two dimensional space on which the relation between the independent variable t and the value of function y is represented has the third axis orthogonal to the space and the axis represents the value of the constant term of y(t). The author names the coordinate axis the constant axis. The function of the interval (0≤t<1) in Eq. (5.69) exists on the two dimensional space that is orthogonal to the axis at the C point of the constant axis. The function of the interval (1≤t) exists on the two dimensional space that is orthogonal to the axis at the point y(0)=C+3/4 of the constant axis. Accordingly, the function in Eq. (5.69) is not joined on this three dimensional space. The cause that the differential is independent of constant term is that the differential is the operation obtaining the partial differential of the function y(t) as to t-axis and that it is independent of the differential as to the constant axis. It is same meaning also that the constant term is subtracted from the operand of the differential. The result of differential is moved to the two dimensional space that exists at the point denoting the constant term of the derivative. Inversely, the integral operation must decide the position of the two dimensional space on which the resultant function exists, so it needs the constant of integral. Usual argument look at the two dimensional space on which all the two dimensional spaces on the three dimensional space are projected at the origin of the constant axis, so the functions in (A) of Eq. (5.68) and in Eq. (5.69) seems to be joined.
. .
Using the unit step function u(t) and the derivative, that is, the impulse function δ(t), it is able to treat the functions in Eq. (5.68) and Eq. (5.69) as the continuous functions existing on one two-dimensional space. Denoting each part that consists of these functions by f(t) and g(t), the total function y(t) may be expressed in Eq. (5.70). Even if f(1)≠g(1) is satisfied, both functions are joined with the unit step function. The unit step function is u(0)=0 and u(+0)=1 but it is infinite times continuously differentiable, so the function y(t) in Eq. (5.70) is continuous function. Accordingly, the definition of continuous function must be changed.
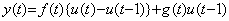 _________(5.70). .
The derivative y'(t) of the function y(t) is expressed in Eq. (5.71). In the case of f(1)=g(1) and f(0)=0, the derivative becomes the function that has joined the derivatives of f(t) and g(t) at t=1 with the unit step functions and that moreover has added the impulse function if f(1)≠g(1). If f(0)≠0, the impulse function exists also at t=0. Furthermore, this function is differentiable infinite times. Accordingly, it is able to define the continuous function as the function that is differentiable infinite times. _________(5.70). .
The derivative y'(t) of the function y(t) is expressed in Eq. (5.71). In the case of f(1)=g(1) and f(0)=0, the derivative becomes the function that has joined the derivatives of f(t) and g(t) at t=1 with the unit step functions and that moreover has added the impulse function if f(1)≠g(1). If f(0)≠0, the impulse function exists also at t=0. Furthermore, this function is differentiable infinite times. Accordingly, it is able to define the continuous function as the function that is differentiable infinite times.
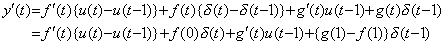 _____(5.71). .
The function y(t) in Eq. (5.54) cannot be transformed into the continuous function with y(0)=0 by multiplying the unit step function. It seems to exist no trouble looking only at the first equation in Eq. (5.72). However, the derivative y'(t) is expressed in the second equation and the impulse function in the second term vanishes at t=0 because the square root of zero is zero but the derivative y'(t) is discontinuous at t=0 because the first term becomes infinity times zero. Accordingly, the function y(t) also is discontinuous at t=0. In the case that the function consisting of Eq. (5.70) is discontinuous function on the existent interval, it is not able to transform the joined function into continuous function even if the unit step function is used. _____(5.71). .
The function y(t) in Eq. (5.54) cannot be transformed into the continuous function with y(0)=0 by multiplying the unit step function. It seems to exist no trouble looking only at the first equation in Eq. (5.72). However, the derivative y'(t) is expressed in the second equation and the impulse function in the second term vanishes at t=0 because the square root of zero is zero but the derivative y'(t) is discontinuous at t=0 because the first term becomes infinity times zero. Accordingly, the function y(t) also is discontinuous at t=0. In the case that the function consisting of Eq. (5.70) is discontinuous function on the existent interval, it is not able to transform the joined function into continuous function even if the unit step function is used.
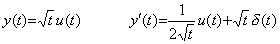 __________(5.72) __________(5.72)
5.5 The norm of operators of this operational calculus.
. .
The product of two vectors YZ is carried out by expanding the left vector into the matrix Y, that is, YZ=YZ. This matrix Y is the operator and denotes the value of operator, so the norm must be equal to the norm of the vector Y. Accordingly, the norm of the operator into which the vector is expanded is the maximum absolute value of function and it is equivalent to the value of the element having the maximum absolute value among the diagonal elements of the matrix Y if the equidistant interval is proper value. The norm is denoted by the matrix into which the norm of the vector ||Y|| is expanded.
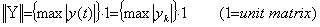 ____(5.73)
The unit matrix in Eq. (5.73) may be omitted, because when all the diagonal elements have an equal value this operational calculus may express the diagonal matrix as the numerical value. ____(5.73)
The unit matrix in Eq. (5.73) may be omitted, because when all the diagonal elements have an equal value this operational calculus may express the diagonal matrix as the numerical value.
. .
It is not able to express the integral operator and the differential operator as the vector forms. The diagonal elements and the lower elements of these operators are equal to those of the operator into which the vector is expanded but the upper elements than the diagonal elements are not all zero. However, the matrix, that is, the value of operator does not vary depending on the operand and also the variable t. In the section 1.2 of the chapter 2, the author said that the integral operator increases the dimensional order. It is due to omit the elements to which the higher order elements of the operand-vector correspond because these elements of operand are all zero. The value of the operator does not change the sign of operand if the variable t varies from the initial point t0 to positive direction. Accordingly, the value of this operator is positive constant and the norm of the operator must be equal to the value of operator.
. .
The difference operator Δ is denoted by the matrix in Eq. (2.5) of the section 2.3. The diagonal and lower elements are all zero but the elements right from diagonal by one column are 1 and the others are all zero. This matrix does not vary according to the operand and variable t, so the value of operator is constant value. Accordingly, the norm of the difference operator Δ must be the same as the value of operator and must be denoted by Δ, that is, ||Δ||=Δ. The product of the norm of difference operator ||Δ|| and the norm of vector ||Y|| becomes zero, denoting the norm ||Y|| by the vector. However, the product of the norm of difference operator ||Δ|| and the norm of the operator into which the vector Y is expanded is not zero. The product of the norms of the vector Y and the vector Z is the same even if it is the product of the norms of vectors or the norms of operators, that is, the norms expanded into the matrixes. However, if the one party has not the vector-form as the difference operator, the other must use the form of matrix.
. .
When the function y(t) has a constant term y0, the difference operation is defined by two ways as Eq. (5.74). The first equation is the operation transforming y(t) into the difference equation with initial value y0 in the same as the differential operation. The second equation is ordinary difference operation obtaining the difference as the function that correspond to the derivative and the operand of this difference operator is y(t)−y0. This operation may be expressed in Eq. (5.75) using the derivative f(t) of the function y(t).
 ______(5.74) ______(5.74)
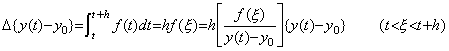 ______(5.75)
Expressing the difference formally in the product of the operator Δ and operand, the value of the operator must be a constant value because the definition of difference operation does not vary according to the operand. However, the case when it is able to carry out the difference operation by the product of the constant value and the operand is only the case when the operand is a linear function as the differential operation. In order that the operation is possible generally, the set whose members are all the pairs of every operand and the mean function of the derivative must be introduced as the operator expressed in [ ] of Eq. (5.75). The set is only one, so the value of operator as set is a constant value and must be 1 because the value of difference operator is decided by the product of h and the value of a member of the set. It is also able to said that h is the value of the set expressed in [ ]. Accordingly, the value and norm of difference operator is ||Δ||=Δ=h. In the case of the differential and integral shown in Eq. (5.45) and Eq. (5.46), it is also able to said that the value of the set whose members are all the pairs of every function and its mean function is the operator t in case of the integral and the operator 1/t in case of the differential. ______(5.75)
Expressing the difference formally in the product of the operator Δ and operand, the value of the operator must be a constant value because the definition of difference operation does not vary according to the operand. However, the case when it is able to carry out the difference operation by the product of the constant value and the operand is only the case when the operand is a linear function as the differential operation. In order that the operation is possible generally, the set whose members are all the pairs of every operand and the mean function of the derivative must be introduced as the operator expressed in [ ] of Eq. (5.75). The set is only one, so the value of operator as set is a constant value and must be 1 because the value of difference operator is decided by the product of h and the value of a member of the set. It is also able to said that h is the value of the set expressed in [ ]. Accordingly, the value and norm of difference operator is ||Δ||=Δ=h. In the case of the differential and integral shown in Eq. (5.45) and Eq. (5.46), it is also able to said that the value of the set whose members are all the pairs of every function and its mean function is the operator t in case of the integral and the operator 1/t in case of the differential.
. .
In case of the differential operator, the elements of the operator expressed in [ ] is the pairs of every operand and its mean function and is decided by only the property of operand. However, the elements of above difference operator are the pairs of every operand and the mean function of the derivative of the operand, so this difference operator is the compound operator including the elements of the differential operator. The difference operator that does not include the elements of the differential operator is denoted by use of the shifting operator E and the identity operator as expressed in Eq. (5.76). The definition of the shifting operator only shifts along the t axis whatever the operand is, so the value of operator is constant value, that is, ||E||=E=1. Accordingly, the value of difference operator has become zero but it is due to the cause that the value of operand and the norm has not the notion of phase. In practice, the value and norm are not zero. Although it is not able to denote the values precisely, the difference operator is ||Δ||=Δ>0 and the shifting operator is ||E||=E>1.
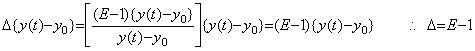 ______(5.76). .
The difference operation in Eq. (5.74) obtains the resultant function whose limit of h→0 becomes identical zero. However, in case of the calculus of finite difference, the result of difference is independent of the interval h. The reason is that the calculus of finite difference transforms the time-variable t into the integer n according to the interval. In case of the time-variable t=t0+nh, the value of function at t0 is denoted by y0, transforming t0 into 0 and the value of function at t is denoted by yn, transforming t into n. Accordingly, The h value is always transformed into h=1, so the value of difference operator does not become 0 and the value of shifting operator does not become 1 and there exist the inverse operators Δ−1 and E−1. ______(5.76). .
The difference operation in Eq. (5.74) obtains the resultant function whose limit of h→0 becomes identical zero. However, in case of the calculus of finite difference, the result of difference is independent of the interval h. The reason is that the calculus of finite difference transforms the time-variable t into the integer n according to the interval. In case of the time-variable t=t0+nh, the value of function at t0 is denoted by y0, transforming t0 into 0 and the value of function at t is denoted by yn, transforming t into n. Accordingly, The h value is always transformed into h=1, so the value of difference operator does not become 0 and the value of shifting operator does not become 1 and there exist the inverse operators Δ−1 and E−1.
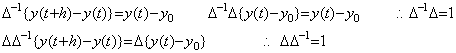 ______(5.77) ______(5.77)
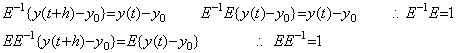 ______(5.78). .
The vector of this operational calculus is the ordered set of sequential finite differences as the operators denoted by the set using [ ] in the equations of the integral, differential and difference. The value of set is the value of vector and the norm, which is the norm of function. The difference operator transforming the vector into the difference of vector is slightly different from above difference operator. As in Eq. (5.79), it is able to make the difference of vector by the product of the difference operator Δ and each element of the vector, which is anything, that is, any function. Accordingly, the value of difference operator is Δ and the norm is also ||Δ||=Δ. In order to multiply the vector instead of the elements by the difference operator Δ, it is required to denote the difference operator by the matrix whose elements at the next column of each diagonal element are 1 and the others are all zero. This matrix is equivalent to the difference operator Δ and Δ>0 is satisfied. The product of the difference operator Δ and the vector is carried out by expanding the difference operator into the matrix as same as the product of two vectors is carried out by expanding the left vector into the matrix. The author names the matrix the expanded matrix of difference operator. ______(5.78). .
The vector of this operational calculus is the ordered set of sequential finite differences as the operators denoted by the set using [ ] in the equations of the integral, differential and difference. The value of set is the value of vector and the norm, which is the norm of function. The difference operator transforming the vector into the difference of vector is slightly different from above difference operator. As in Eq. (5.79), it is able to make the difference of vector by the product of the difference operator Δ and each element of the vector, which is anything, that is, any function. Accordingly, the value of difference operator is Δ and the norm is also ||Δ||=Δ. In order to multiply the vector instead of the elements by the difference operator Δ, it is required to denote the difference operator by the matrix whose elements at the next column of each diagonal element are 1 and the others are all zero. This matrix is equivalent to the difference operator Δ and Δ>0 is satisfied. The product of the difference operator Δ and the vector is carried out by expanding the difference operator into the matrix as same as the product of two vectors is carried out by expanding the left vector into the matrix. The author names the matrix the expanded matrix of difference operator.
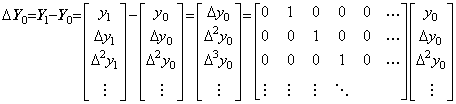 ______(5.79). .
The expanded matrix of difference operator Δ has not the inverse matrix but the difference operator Δ has the inverse operator. Strictly speaking, the vector of operand for the difference operator in Eq. (5.79) must be what is subtracted the initial value y0 from the vector. Accordingly, the operation must be expressed in Eq. (5.80). However, it has no trouble to express in Eq. (5.79), because the first column of the expanded matrix of difference operator Δ has the elements that are all zero and it means to remove the initial value by subtracting. On the other hand, the inverse operation must be the inverse operation for Eq. (5.80) in which the initial value is subtracted explicitly, so it is expressed in Eq. (5.81). The norm of the inverse operator is ||Δ−1||=Δ−1. ______(5.79). .
The expanded matrix of difference operator Δ has not the inverse matrix but the difference operator Δ has the inverse operator. Strictly speaking, the vector of operand for the difference operator in Eq. (5.79) must be what is subtracted the initial value y0 from the vector. Accordingly, the operation must be expressed in Eq. (5.80). However, it has no trouble to express in Eq. (5.79), because the first column of the expanded matrix of difference operator Δ has the elements that are all zero and it means to remove the initial value by subtracting. On the other hand, the inverse operation must be the inverse operation for Eq. (5.80) in which the initial value is subtracted explicitly, so it is expressed in Eq. (5.81). The norm of the inverse operator is ||Δ−1||=Δ−1.
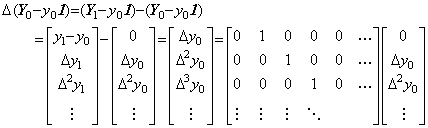 ______(5.80) ______(5.80)
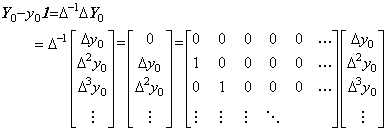 ______(5.81). .
The matrix operation shifts down each element of the operand vector ΔY0 to next row and sets zero to the first row, because the first row of the expanded matrix of Δ−1 has the elements that are all zero. In case of multiplying each element of the operand vector ΔY0 by Δ−1, the operation may use Δ−1Δ=1 and y0=0. In usual, it is said that the product of the difference operator and the inverse operator is ΔΔ−1=1 but Δ−1Δ≠1. It is due to wrong argument thinking that the difference operator transforms the initial value into zero. It is right thinking that the operand of difference operator is the function whose initial value is subtracted. Accordingly, the initial value of operand must be zero. Expanding both of the difference operator and the inverse operator into the matrices, the product of both becomes ΔΔ−1=1, that is, the unit matrix but Δ−1Δ≠1 because the first row and first column of Δ−1Δ is zero as shown in Eq. (5.82). However, because the first element of the operand vector is y0=0, there is no difference in cases that the first row and first column is 1 or 0 and so the product is Δ−1Δ=1. ______(5.81). .
The matrix operation shifts down each element of the operand vector ΔY0 to next row and sets zero to the first row, because the first row of the expanded matrix of Δ−1 has the elements that are all zero. In case of multiplying each element of the operand vector ΔY0 by Δ−1, the operation may use Δ−1Δ=1 and y0=0. In usual, it is said that the product of the difference operator and the inverse operator is ΔΔ−1=1 but Δ−1Δ≠1. It is due to wrong argument thinking that the difference operator transforms the initial value into zero. It is right thinking that the operand of difference operator is the function whose initial value is subtracted. Accordingly, the initial value of operand must be zero. Expanding both of the difference operator and the inverse operator into the matrices, the product of both becomes ΔΔ−1=1, that is, the unit matrix but Δ−1Δ≠1 because the first row and first column of Δ−1Δ is zero as shown in Eq. (5.82). However, because the first element of the operand vector is y0=0, there is no difference in cases that the first row and first column is 1 or 0 and so the product is Δ−1Δ=1.
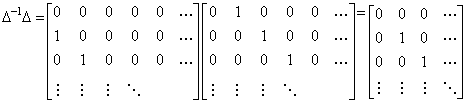 ______(5.82). .
The shifting operator is expressed in as follows and is ||E||=E. The expanded matrix of shifting operator E is the sum of the unit matrix and the matrix into which the difference operator Δ is expanded. This matrix has the inverse matrix and it is the matrix into which the inverse operator E−1 is expanded. The norm of the inverse operator is ||E−1||=E−1. ______(5.82). .
The shifting operator is expressed in as follows and is ||E||=E. The expanded matrix of shifting operator E is the sum of the unit matrix and the matrix into which the difference operator Δ is expanded. This matrix has the inverse matrix and it is the matrix into which the inverse operator E−1 is expanded. The norm of the inverse operator is ||E−1||=E−1.
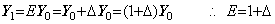 ______(5.83). .
The differential operation is expressed in Eq. (3.37) of the section 3.5. The operand vector is Y0−y01, so the vector has the initial value, that is, the first element whose value is zero. The difference operator Δ removes the first element and the operand vector may be denoted by ΔY0 as shown in Eq. (5.84). The vector h−1ΔY0 corresponds to the function f(ξ t) that denotes the differential mean value of the function y(t). Accordingly, the matrix D corresponds to the operator that transforms the mean function f(ξ t) into the function f(t) in Eq. (5.46) but the value of the matrix D is not 1. The differential mean value of the function y(t) on equidistant interval is f(ξ)=h−1{y(t+h)−y(t)}, so the point ξ is t<ξ<t+h and is not equidistant point. Accordingly, in order to transform the vector corresponding to the mean function f(ξ t) into the vector of the function f(t), that is, the derivative y'(t), the compensation of phase is needed and it is the reason by which the operator value of the matrix D is not 1. However, this matrix is only one, so the value of operator is constant value. In the case that the differences on and after the fourth order difference of ΔY0 are all zero, the matrix D may be expressed in the matrix that has 3 rows and 3 columns. It dose not mean that there exists another matrix D and it only means that other elements are omitted because expressing these has no meaning. In this operational calculus, the value and norm of differential operator are denoted by ||h−1D||=h−1D and the matrix into which the differential operator is expanded. ______(5.83). .
The differential operation is expressed in Eq. (3.37) of the section 3.5. The operand vector is Y0−y01, so the vector has the initial value, that is, the first element whose value is zero. The difference operator Δ removes the first element and the operand vector may be denoted by ΔY0 as shown in Eq. (5.84). The vector h−1ΔY0 corresponds to the function f(ξ t) that denotes the differential mean value of the function y(t). Accordingly, the matrix D corresponds to the operator that transforms the mean function f(ξ t) into the function f(t) in Eq. (5.46) but the value of the matrix D is not 1. The differential mean value of the function y(t) on equidistant interval is f(ξ)=h−1{y(t+h)−y(t)}, so the point ξ is t<ξ<t+h and is not equidistant point. Accordingly, in order to transform the vector corresponding to the mean function f(ξ t) into the vector of the function f(t), that is, the derivative y'(t), the compensation of phase is needed and it is the reason by which the operator value of the matrix D is not 1. However, this matrix is only one, so the value of operator is constant value. In the case that the differences on and after the fourth order difference of ΔY0 are all zero, the matrix D may be expressed in the matrix that has 3 rows and 3 columns. It dose not mean that there exists another matrix D and it only means that other elements are omitted because expressing these has no meaning. In this operational calculus, the value and norm of differential operator are denoted by ||h−1D||=h−1D and the matrix into which the differential operator is expanded.
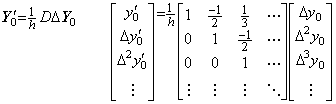 ______(5.84). .
The integral operation is expressed in Eq. (4.28) of the sector 4.4 and the result is the vector Y0−y01. The first element is zero but it may be expressed in the vector ΔY0 because the difference operator Δ removes the first element. The product of the matrix and the operand vector in Eq. (5.85) denotes the mean function of integral but the operator value of the matrix D−1 is not 1. It is different from the operator that transforms the integrand into the mean function in Eq. (5.45). The point ξ t at which the integrand f(t)=y'(t) gives the mean value of integral f(ξ t) does not exist on the points that has divided the integrand with equidistant interval, so the compensation of phase is needed, in order to transform the vector corresponding to the mean function f(ξ t) into the vector whose elements are calculated by the equidistant points of the integrand. This is the reason why the operator value of the matrix D−1 is not 1. However, the matrix D−1 exists only one, so the value and norm of the integral operator are constant value and are denoted by ||hD−1||=hD−1. It is the matrix into which the integral operator is expanded. ______(5.84). .
The integral operation is expressed in Eq. (4.28) of the sector 4.4 and the result is the vector Y0−y01. The first element is zero but it may be expressed in the vector ΔY0 because the difference operator Δ removes the first element. The product of the matrix and the operand vector in Eq. (5.85) denotes the mean function of integral but the operator value of the matrix D−1 is not 1. It is different from the operator that transforms the integrand into the mean function in Eq. (5.45). The point ξ t at which the integrand f(t)=y'(t) gives the mean value of integral f(ξ t) does not exist on the points that has divided the integrand with equidistant interval, so the compensation of phase is needed, in order to transform the vector corresponding to the mean function f(ξ t) into the vector whose elements are calculated by the equidistant points of the integrand. This is the reason why the operator value of the matrix D−1 is not 1. However, the matrix D−1 exists only one, so the value and norm of the integral operator are constant value and are denoted by ||hD−1||=hD−1. It is the matrix into which the integral operator is expanded.
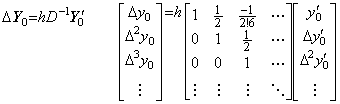 ______(5.85) ______(5.85)
Return to CONTENTS
|
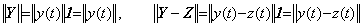 _____(5.1)
_____(5.1)
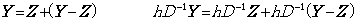 _____(5.1a)
_____(5.1a)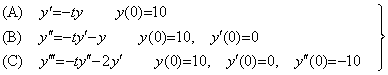
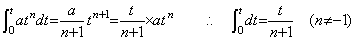 _____(5.2)
_____(5.2)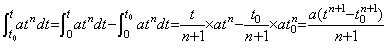 ____(5.3)
____(5.3)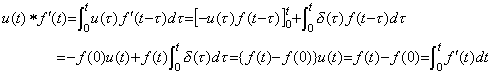 __(5.4)
__(5.4)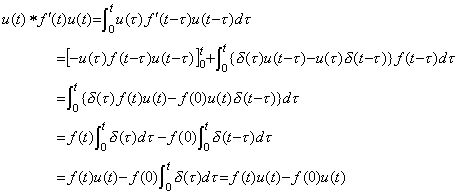 __(5.5)
__(5.5)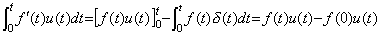 _____(5.6)
_____(5.6)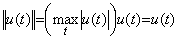 ________(5.7)
________(5.7)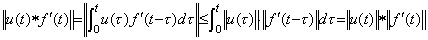 ____(5.8)
____(5.8)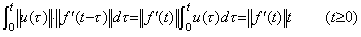 _____(5.9)
_____(5.9)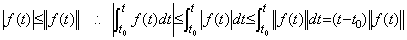 ____(5.10)
____(5.10)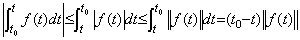 _____(5.11)
_____(5.11)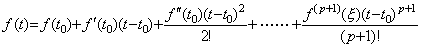 ____(5.12)
____(5.12)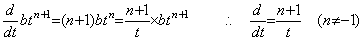 _____(5.13)
_____(5.13)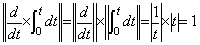 ______(5.14)
______(5.14)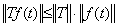 ______(5.15)
______(5.15)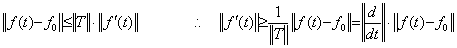 _____(5.16)
_____(5.16)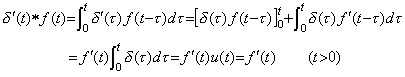 ____(5.17)
____(5.17)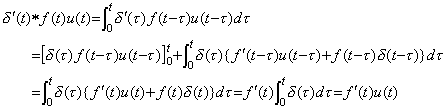 ___(5.18)
___(5.18) ___(5.19)
___(5.19)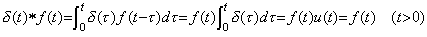 ____(5.20)
____(5.20)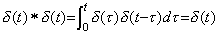 ______(5.21)
______(5.21)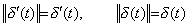 ________(5.22)
________(5.22)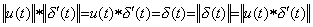 ____(5.23)
____(5.23)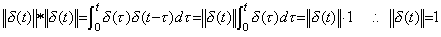 ___(5.24)
___(5.24)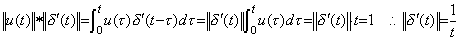 ___(5.25)
___(5.25)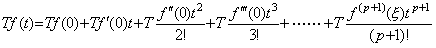 ___(5.26)
___(5.26)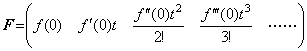 ____(5.27)
____(5.27)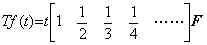 ____(5.28)
____(5.28)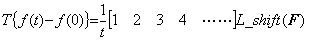 _____(5.29)
_____(5.29)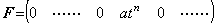 _____(5.30)
_____(5.30)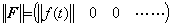 ____(5.31)
____(5.31)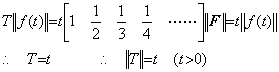 ____(5.32)
____(5.32)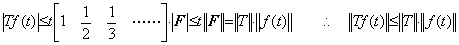 ___(5.33)
___(5.33)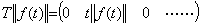 ____(5.34)
____(5.34)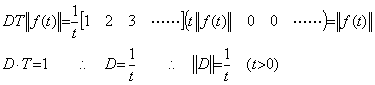 _____(5.35)
_____(5.35)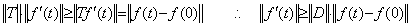 _____(5.36)
_____(5.36)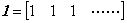 ________(5.37)
________(5.37)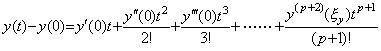 ____(5.38)
____(5.38) _____(5.39)
_____(5.39) _____(5.40)
_____(5.40)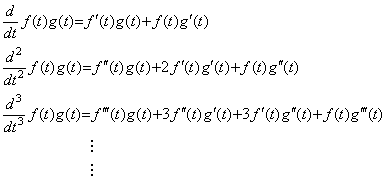 ____(5.41)
____(5.41)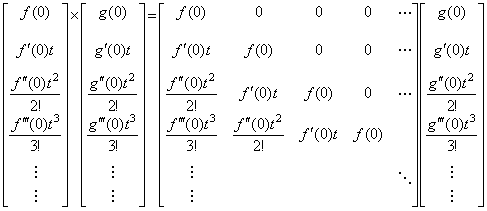 ___(5.42)
___(5.42)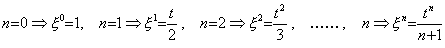 _______(5.43)
_______(5.43)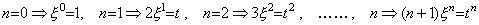 _________(5.44)
_________(5.44)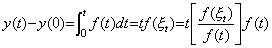 _____(5.45)
_____(5.45)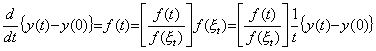 _____(5.46)
_____(5.46)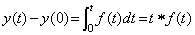 _______(5.47)
_______(5.47)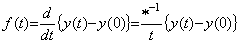 ____(5.48)
____(5.48)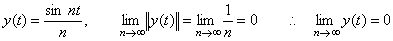 _____(5.49)
_____(5.49)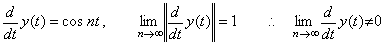 _____(5.50)
_____(5.50)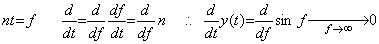 _____(5.51)
_____(5.51)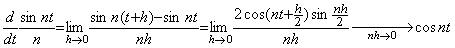 _____(5.52)
_____(5.52)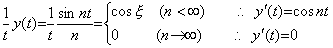 ____(5.53)
____(5.53)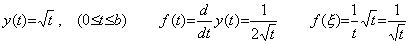 ____(5.54)
____(5.54)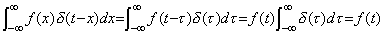 _____(5.55)
_____(5.55)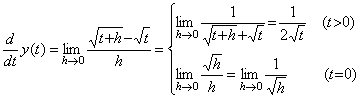 _____(5.56)
_____(5.56)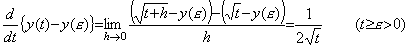 _____(5.57)
_____(5.57)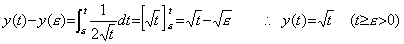 ________(5.58)
________(5.58)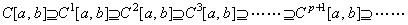 ______(5.59)
______(5.59)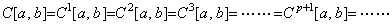 _______(5.60)
_______(5.60)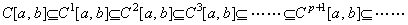 _____(5.61)____[Q.E.D.]
_____(5.61)____[Q.E.D.]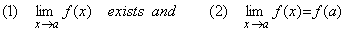 ______(5.62)
______(5.62)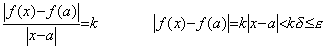 ______(5.63)
______(5.63) _______(5.64)
_______(5.64)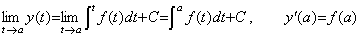 ______(5.65)_____[Q.E.D.]
______(5.65)_____[Q.E.D.]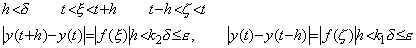 _______(5.66)
_______(5.66)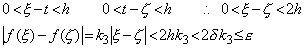 ______(5.67)
______(5.67)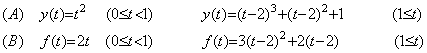 ____(5.68)
____(5.68)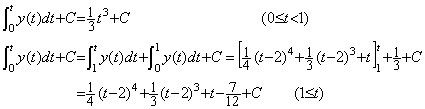 ____(5.69)
____(5.69) _________(5.70)
_________(5.70)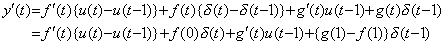 _____(5.71)
_____(5.71)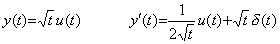 __________(5.72)
__________(5.72)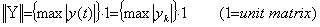 ____(5.73)
____(5.73)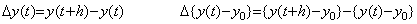 ______(5.74)
______(5.74)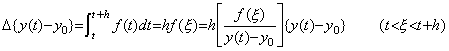 ______(5.75)
______(5.75)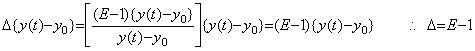 ______(5.76)
______(5.76)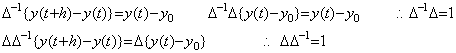 ______(5.77)
______(5.77)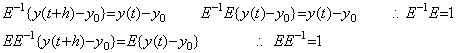 ______(5.78)
______(5.78)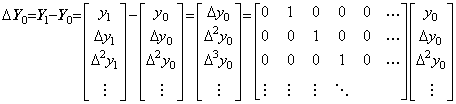 ______(5.79)
______(5.79)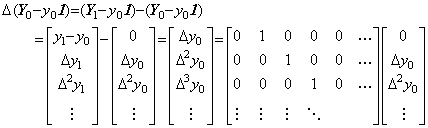 ______(5.80)
______(5.80)
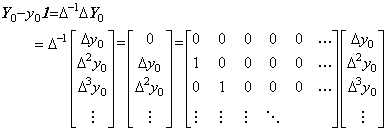 ______(5.81)
______(5.81) ______(5.82)
______(5.82)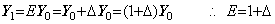 ______(5.83)
______(5.83)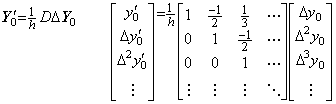 ______(5.84)
______(5.84)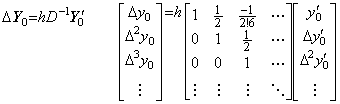 ______(5.85)
______(5.85)