2. The operators.
2.1 The quotient without the vector form.
. .
When the vector W is the product of two vectors Y, Z, the quotient W/Z is the vector Y. However, there does not always exist the vector which is the quotient of any two vectors. There is such a vector W that W=AZ is satisfied, when the matrix A is any square matrix. However, it does not always hold W=AZ for the matrices W, Z into which the vectors W and Z are expanded respectively, because the product of matrix AZ is not always triangular. Even if it is triangular, it does not always satisfy the condition for the expansion of vectors mentioned in section 1.4. Therefore the concept of the quotient must be expanded further to these matrices. It is similar to the expansion of the system of the integer numbers to the system of the rational numbers.
. .
The author calls the matrix A the operator, if a square matrix A and a vector Z satisfy the equality W=AZ. If W=0, the determinant of the matrix is det(A)=0 or the vector is Z=0. If Z=0, the matrix A is indefinite and not quotient. When Z≠0 and det(A)=0, if A=0, the matrix A is quotient but if not so, the matrix A is indefinite and not quotient except of the expanded quotient of vectors, because W=0 is also satisfied for 2A, 3A, ………. It is not able to obtain these non-quotient operators by the relation of the vector 0 and the vector Z. All of the nonzero elements of these matrices must be given previously and it is not able to express the matrices in the form of quotient. These operators are unique by that all of the nonzero elements have the given values so that the solution of differential equation becomes unique by given the initial values. When the matrix A is quotient and W=AZ, if there exists the nonzero matrix B which satisfies 0=BZ, it satisfies W=(A+B)Z. In the case, the matrices B and (A+B) are indefinite because of det(B)=0. Denoting the values of nonzero elements of the matrix B by bij, the corresponding elements aij of the matrix A must be given and if bij≠aij, it is resulted that the matrix B dose not exist. If bij=aij, the matrix B is the partial matrix of A and the matrix (A+B) dose not exist. By above reason, the author defines the quotient without vector form as follows.
. . [Definition] When a vector W and a vector Z≠0 are related by a square matrix A as W=AZ, if A=0 is satisfied for W=0 the author defines the matrix A as quotient, provided that if there exists the matrix B such that 0=BZ is satisfied all the elements of the matrix A correspond to nonzero elements of the matrix B are known previously.
. .
[Theorem 2.1]. .The quotient without the vector form is unique.
[Proof]. .
Supposing the matrices A and B are the quotients without the vector form and supposing W =AZ and W =BZ for Z≠0, Eq. (2.1) must be satisfied.
. .
There exist the two matrices A and B, which have the same result for a vector Z as below. The matrix A−B has zero on all the elements except of the second column so (A−B)Z is zero, whereas A−B is not zero. The second column of the matrices A and B may have arbitrary values because the second component of Z is zero.
_____
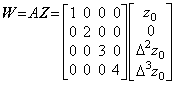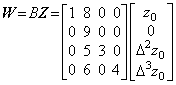______(2.2) . . There are the two cases when A≠0 and det(A)=0 are satisfied in the equality W=AZ. When the matrix A is the expansion of a vector, it is the expanded quotient mentioned in section 1.6 and when it has not the vector form, it is the operator and not the quotient. In this case, if there exist the matrix B such that det(B)=0 and 0=BZ are satisfied for Z≠0, the equality W=(A+B)Z is satisfied, so the operator is not unique but the operator becomes unique by appending the condition that the elements of the matrix A corresponding to nonzero elements of the matrix B are known previously because the matrix (A+B) is not operator satisfying W=AZ.
. . When det(A)≠0 is satisfied in the equality W=AZ, there exists the inverse matrix uniquely and the inverse operation is expressed in Z=A−1W and when det(A)=0 is satisfied, there dose not exist the inverse matrix. However, when the matrix A is operator it is able to define the inverse operator by no use of the determinant. For example, when the operator A of the first equation in Eq. (2.2) has zero on the fourth diagonal elements it is denoted by Eq. (2.2a). The fourth diagonal element of the inverse operator B in the second equation is 1/0=∞ and in order to obtain the original vector Z, the fourth element Δ3z0 must be given previously. Accordingly, in order that the value is not influenced by calculation of the right side, the fourth diagonal element of the inverse operator B is set zero. The product BA of both operators is same as unit matrix except the fourth diagonal element is zero. In these case, there exists the supposition that the inverse operator B and the identity operator BA do not carry out the calculation of the given element Δ3z0. However, if the calculation is carried out, the value Δ3z0 becomes zero, so the operation must add the given value to the element. Usual inverse operator and identity operator denote these operators with adding operation so these are complex operator. This operational calculus also uses the former inverse operator and it is able to define the inverse operator by following [Definition].
_____
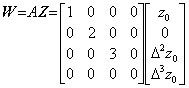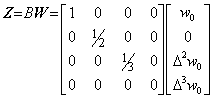______(2.2a). . This inverse operator is obtained by the way solving the simultaneous linear equation constructed so that the product BA of the operator A and the inverse operator B whose elements are all unknown becomes the unit matrix. In the case, the elements whose values are indefinite or impossible are set zero. In case Eq. (2.2a), the number of variables is 16 and the number of equations is 16 so the solution is obtained. The product of the first row of B and the first column of A gives b11=1. The product of the second row of B and the second column of A gives b22=1/2. The product of the third row of B and the third column of A gives b33=1/3. The product of the fourth row of B and the fourth column of A becomes b44×0=1 and the solution is impossible so b44=0 is set. All the other elements are zero. Hence, the matrix in the second equation of Eq. (2.2a) is obtained. In this inverse operation, the value of Δ3z0 must be given the value Δ3z0, which the vector Z had before transformed into the vector W by A.
. .
[Theorem 2.2]. .The inverse operator is unique.
[Proof]. .Supposing there exist two inverse operators for the operator A of W=AZ and denoting them B and C, the equalities Z=BW and Z=CW are satisfied so 0=(B−C)W and det(B−C)=0 are satisfied. If B−C≠0, the operator B must have the same values as the operator C for the elements correspond to nonzero elements of the matrix (B−C). This is contradictory to supposition B−C≠0, so B−C=0 is satisfied.__________[Q.E.D.]
. .
There exists the operator whose elements on the first column are all zero. In usual concept of mapping, the inverse operation for it is not unique because the initial value is indefinite. In the case, it is considered that the mapping by the operator lost the initial value. This operational calculus considers that the initial value is remained in the original space and that the inverse operation uses it because the inverse operation is the mapping to the original space. This is meant by that the initial value must be known or given or by that inverse operation recovers the original vector or function. The differential operation is defined usually by the first equation of Eq. (2.2c). However, the rigorous definition must be the second equation of Eq. (2.2c) and the operand of the differential operator is y(t)−y0. Hence, it is satisfied that if the operated result is identical with zero the operand is identical with zero.
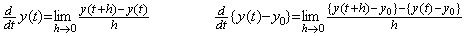____(2.2c)
________(2.2d)
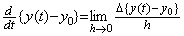
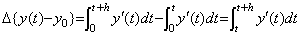
2.2 The system of operators.
. .
When the vector W and Z are expressed in W=AZ by use of a matrix A, the author defines the matrix A as the operator. The operator holds the four operations as follows.
. .[Theorem 2.3]. .The sum and remainder of two operators are also operators.
[Proof]. .Supposing W=AZ and Y=BZ for operators A, B and any vector Z,
[Proof]. .Supposing W=AY and Y=BZ for operators A, B and any vector Z,
| A. | . .For all operators A, B, C, | |
| (A1). .A+B=B+A | (A2). .(A+B)+C=A+(B+C) | |
| (A3). .There exists an operator 0, such that A+0=A. | ||
| (A4). .For every operator A there exists an operator −A, such that A+(−A)=0. | ||
| B. | . .For all operators A, B, C, | |
| (B1). .(AB)T=BTAT | (B2). .(AB)C=A(BC) | |
| (B3). .A(B+C)=AB+AC | (B4). .(B+C)A=BA+CA | |
| C. | . .For all operators A, B and scalars α, β, | |
| (C1). .1•A=A | (C2). .α(βA)=(αβ)A | |
| (C3). .(α+β)A=αA+βA | (C4). .α(A+B)=αA+αB | |
. . [Theorem 2.5]. .The quotient of operators is also an operator.
[Proof]. .Suppose W=CZ and Y=BZ for arbitrary operators C, B(≠0) and any vector Z≠0. When there exists the matrix A which satisfies C=AB, the vector of the i-th row of the operator C and the vector of the i-th row of the matrix A is expressed in Ci=AiB so Ai is the solution of the simultaneous equation.
If det(B)=0, the solution Ai is indefinite so the matrix A is indefinite and not quotient.
If det(B)≠0, the solution Ai is unique so the matrix A is unique and quotient.
By the supposition,
. . Since the four operations of operators have been found as mentioned above, it is able to define the operator-valued function whose independent variable is operator. It will be mentioned afterwards. By Theorems mentioned below, the vector-valued function is also the operator-valued function when the vectors are expanded into the matrices.
. .
[Theorem 2.6]. .The vector is an operator.
[Proof]. .Any vector Y is able to be expanded into the matrix Y and,
| Y=Y1=Y1 | [Q.E.D.] |
. . [Theorem 2.7]. .The quotient of vectors is an operator.
[Proof]. .The quotient of vectors W/Z is expressed in W=AZ or W=YZ=YZ, where the matrix Y is the expansion of the vector Y.______[Q.E.D.]
. .
Although the vector is an operator, the commutative law of multiplication is always held. It must be noted that the property differs from that of the other operators, which do not always hold the law and needs the reversal law of transposed product usually. Hence, when there exist the continued products of vectors and operators, it is not permissive to take the commutative or associative operation which cause the contradictory result as the products of matrices. For example, the products of an operator A and vectors Y, Z in Eq.(2.3) is correct because the product AZ is a vector. However, it is not always permissive to change the right side into A(ZY) or A(YZ) further, because it is the same result as incorrect commutative operation on the product of the vector Y and the matrix A.
| Y(AZ)=(AZ)Y | (2.3) |
. . The norm of the operator which is a vector is the norm of the vector. It is not easy to define the norm of the other operators as the maximum quantity. However, the operators which we usually use in numerical calculus has the simple properties as mentioned in following sections and the norm can easily be defined. It will be mentioned afterwards.
. . Here, it follows that there is the system in which the operators are the uppermost concept of the quantities which can be associated by four operations. It is constructed as follows.
. . The operators in usual operational calculus are also the uppermost concept which includes the systems of numbers, functions and mathematical operations. Hence it must be able to carry out four operations between them. Mikusinski expanded the concept of multiplication into the convolution integral in order to express the integral of a function in the product of the operator and function and he defined the operator as the quotient. Laplace transform does not use the expansion explicitly by transforming the function f(t) of the real variable t into a new function F(s) of the subsidiary variable s, which may be real or complex.
. . The author's operational calculus does not expand the concept of multiplication and be able to express the operation of a function in the product of the operator and function by transforming the operator into the matrix and the function and numbers into the vectors. Hence the four operations come to those of the matrices and vectors, where the vector as the multiplicand is expanded into the matrix when the multiplication of two vectors is carried out.
2.3 The difference operator.
. .
The difference of vectors ΔY0=Y1−Y0 defined in Section 1.3 can be expressed in the product of the matrix and vector in Eq.(2.5). The vector Y0 is defined by the differences of y0 to yp and the vector Y1 is defined by the differences of y1 to yp+1, so the vector ΔY0 is defined by the differences of y0 to yp+1. In this range, the vector Y0 consists of the components from y0 to Δp+1y0, that is, it exists in the p+2 dimensional space. The rightest side of Eq.(2.5) represents that the vector ΔY0 is the projection of the vector Y0 into the p+1 dimensional subspace which consists of the components from Δy0 to Δp+1y0.
. .
On the other hand, the vector Y0 in the first right side Y1−Y0 is the projection of the vector Y0 in the rightest side into the p+1 dimensional subspace which consists of the components from y0 to Δpy0. It is able to use the same denotation for the both vectors if there is no danger of confusion, because the projection is the truncation of the component Δp+1y0. The component is negligible for the vector Y0 in the p+1 dimensional subspace but it is not always negligible for the vector ΔY0. Hence the vector ΔY0 has the component and the component Δp+2y0 is omitted because it is zero by the product of the matrix and vector. It shows that the component Δp+1y1 is equal to the component Δp+1y0 in proper precision.
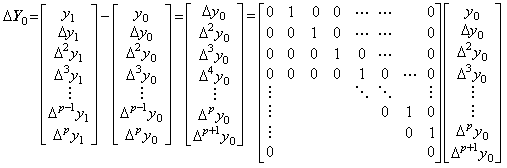. .(2.5). . The matrix in above equation is the square matrix which has the values 1 only in the next after cells of the principal diagonal and the values 0 in the other cells. The character Δ followed by the vector Y0 denotes the matrix and differs from the character Δ used in the components of the vector because this only shows the difference of two numbers. However, the result of the matrix equation is equivalent to the product of Δ and the vector Y0, if the character Δ is thought as a scalar. Hence it does not need to distinguish between them so these are denoted by the same character.
. . Supposing Y0=(c, 0, 0, ……), the product of Δ and Y0 comes to ΔY0=0, whereas the matrix Δ is not zero. Hence the matrix Δ is not the quotient of the vector 0 by the vector Y0 but the operator mentioned in Section 2.2. If the vector Y0 is expanded into the matrix Y0, the product of Δ and Y0 is not zero as expressed in Eq.(2.6). Hence the operator Δ is the quotient of the operator in the left side by the operator Y0. These are similar to the relation that the product of 0.1 and 3 is zero in the integer number but 0.3 in the real number. The author defines the matrix Δ as the difference operator.
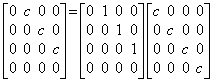_____(2.6). . The difference operator Δ removes the first component from the following vector, shifting every component to the upper cell by one as in Eq.(2.5). In the last cell, it shifts the component which was being truncated. If the component is truncated because of zero, the number of components may be decreased by one. When any operator is premultiplied by Δ, the every column of the operator is shifted by one cell as mentioned above. Hence the difference operator Δ removes the first row from the following operator, shifting every row to the upper row by one. On the last row, it shifts the next row which was being omitted in the expression of the operator. When any operator is postmultiplied by Δ, the every row of the operator is shifted by one cell to the right. Hence the difference operator Δ removes the last column from the preceding operator, shifting every column to the right column by one. On the first column it fills zero because the cells on the first column of Δ are all zero.
. . If the matrix A is the triangular matrix which consists of the rows having the same elements with the upper row except the elements are shifted to the right by one cell and the first cell is given zero, the product of Δ and the matrix A is commutative, that is, ΔA=AΔ as expressed in Eq.(2.7).
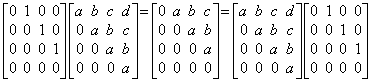____(2.7)
2.4 The summation operator.
. .
The difference operator Δ has not the inverse matrix because its determinant is det(Δ)=0. However, there exists the inverse operator which recover the vector Y0 from the product of Δ and Y0, if the initial value y0 is held in the inverse operation. Denoting it as Δ−1, it is defined in Eq.(2.8) and named the summation operator. This inverse operator includes the adding operator. The difference operator is usually defined by Δy(t)=y(t+h)−y(t) but rigorously defined by Δ{y(t)−y0}={
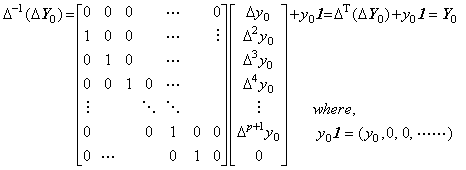___(2.8). .
The constant vector y01 in Eq.(2.8) must be expressed in the left side of Eq.(2.9) in rigorous expression because it just means the first component of the vector Y0. The matrix unit is the operator but not the quotient of the vector y01 by Y0 because if y0 is zero, the product of the matrix unit and Y0 comes to zero. Therefore Eq.(2.10) is contradictory because
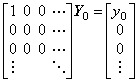____(2.9)_______
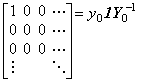____(2.10)
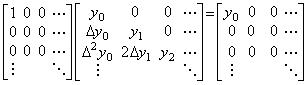_____(2.11). . [Theorem 2.8]________ ΔΔ−1=Δ−1Δ=1.
[Proof]. . Replacing U0Y0 for y01 in Eq.(2.8), we obtain,
| Therefore, | ΔΔ−1=ΔΔT=1 | [Q.E.D.] |
. . In usual theory, the difference operator premultiplied by the inverse operator does not come to the identity operator, where the operator postmultiplied by the inverse operator comes to the identity operator. The operator ΔT corresponds to the usual inverse operator as shown in Eq.(2.8). However, the operator ΔT is not denoted as the inverse operator Δ−1 of the difference operator in this operational calculus, because the product ΔTΔ is not the identity operator as shown in Eq.(2.13). This operator is the inverse operator which is required not to carry out the calculation of the initial value as mentioned in Section 2.1 because it is given. The inverse operator Δ−1 denotes the inverse operation including the operation to add the initial value. However, if the operand is the function y(t)−y0, it is able to use these operators as same operator.
. . The operator ΔT shifts the every row of the matrix premultiplied by it to the under row by one, omitting the last row in order to express the resultant matrix in square. Then it fills the first row with zero. However, the operator Δ−1 recovers the first row given previously. The relation is expressed in Eq.(2.14) by postmultiplying the every side of Eq.(2.13) by any matrix M.
2.5 The shifting operator.
. .
The author defines the operator which gives the vector Y1 for the vector Y0 as the shifting operator and denotes it by the character E. The operator is related to the difference operator by Eq.(2.15).
________
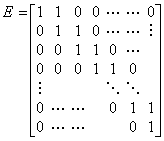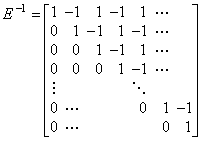
. . [Theorem 2.9]________Y0=E−1Y1
[Proof]. .Let us suppose
1). .The last component of E−1Y1 is Δp+1y1. It is equal to Δp+1y0 because it is the last component of __Y1=EY0.
2). .The (p+1)th component of E−1Y1 is,
. . Hence the (p−j)th component of E−1Y1 is,
. . The matrix E−1 is the operator which gives the vector Y0 for the vector Y1, so it is the inverse shifting operator.
2.6 The operator-valued functions.
. .
The author defines the function which gives the operator Y for an operator-valued variable X as the operator-valued function and denotes it by Y=F(X). The vector-valued function F(X) is the operator-valued function if the vectors are expanded into the matrix. For example, the vector-valued function
. .
The shifting operator E is the operator value of the linear function Y=X+1 for X=Δ and the inverse shifting operator E−1 is the operator value of the function Y=(X+1)−1 for X=Δ. Inversely, the difference operator Δ is the operator value of the inverse function X=Y−1 for Y=E and the summation operator Δ−1 is the operator value of the function X=(Y−1)−1 for Y=E. The summation operator is also the operator value of the implicit function YX=ΔTX+U0 or YX=1 for X=Δ by Eq.(2.13).
. .
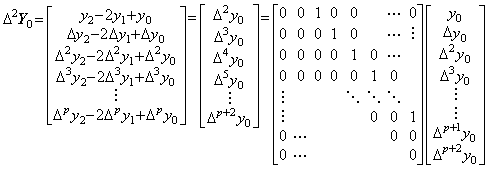
The operator Δ2 is the operator value of the function Y=X2 for X=Δ and is obtained by the product Δ×Δ. It comes to the matrix which has the values 1 in the second right cells of the principal diagonal and the values 0 in all the other cells as shown in Eq.(2.16), because the multiplicand Δ shifts the every row of the multiplier Δ to the upper row by one. In general, the operator Δp is the operator value of the p-th power function Y=Xp for X=Δ and the matrix which has the values 1 in the p-th right cells of the principal diagonal and the values 0 in all the other cells.
___(2.16). . [Theorem 2.10]. .
______(2.17)[Proof]. .1). .If p=1,. .
2). .If p=2,
3). .Supposing that Eq.(2.17) is held when p=n,
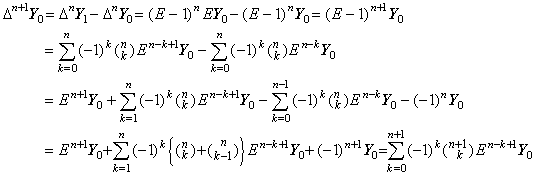
| [Q.E.D.] |
. . [Theorem 2.11]. .
______(2.18)[Proof]. .1). .If p=1,. .
2). .If p=2,. .
3). .Supposing that Eq.(2.18) is held when p=n, when p=n+1,
. .
[Theorem 2.12]. .The inverse operator of the n-th order difference operator is expressed in Eq.(2.19) implicitly.
____(2.19)[Proof]. .1). .If n=2, replacing ΔY0 and Δy0 on Y0 and y0 of Eq.(2.8),
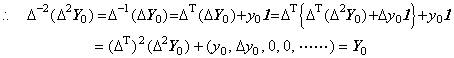
2). .Supposing that Eq.(2.19) is held for n=k,
. . Hence if n=k+1, replacing ΔY0, Δy0, ......, Δky0 on Y0, y0, ......, Δk−1y0 respectively,
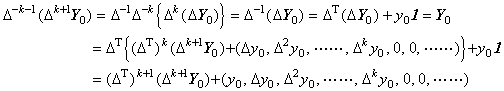
| [Q.E.D.] |
Return to CONTENTS