Chapter 3. The operational calculus.
1. The vectors.
1.1 The definitions of vectors.
. .
When y0, y1, y2, y3, ………, yp are the values of y(t) for equidistant variables tk=t0+kh, k=0, 1, 2, 3, ……, p, the author defines the ordered set of the finite differences in the right side of Eq.(1.1) as the ordered set of the function at t=t0. The ordered set may be represented by such capital or small letters in bold-faced type as the left side of Eq.(1.1). Usually the letters would denote the first member of the ordered set, if there is no danger of confusion.
. . The ordered set represents Newton's interpolation formula without remainder term. Hence, if Newton's interpolation formula of y(t) has zero or negligible remainder term on the interval [t0, tp], it is equivalent to y(t). However, if the remainder term is not negligible, it is equal to y(t) only at the equidistant points tk. It may be defined by the backward differences but it comes to the same thing. So the author always uses the forward differences.
. . The ordered set of the function y(t) at t=t1 is defined by use of the subscript 1 and represents Newton's interpolation formula without remainder term on the interval [t1, tp+1]. In general, the ordered set of the function y(t) at t=tk is defined by use of the subscript k and represents that formula on the interval [tk, tp+k]. However, if there is no danger of confusion, the subscript may be omitted.
. . The author defines the addition of the ordered set Y0 of a function y(t) and the ordered set Z0 of a function z(t) as the ordered set of the added function y(t)+z(t) so it comes to the ordered set expressed in Eq.(1.2). The subtraction of the ordered sets also comes to the ordered set with the subtracted members. In the case, if all the resultant members are zero, the ordered set is defined as zero. Even if the two functions are different at all the points except of the equidistant points tk, the subtraction of the ordered sets is zero because all the both finite differences are equal respectively. In this case, it is defined that the both ordered sets are equal.
. . When α is any number, the author defines the ordered set αY0 as the ordered set of the function αy(t) so it comes to the ordered set with the members which are α times the each member of Y0.
. . By These definitions, the three ordered sets W, Y, Z of any three functions evidently hold the following properties of vector space.
| A. | . .For all vectors W, Y, Z, | |
| (A1). .Y+Z=Z+Y | (A2). .(Y+Z)+W=Y+(Z+W) | |
| (A3). .There exists a vector 0, such that Y+0=Y. | ||
| (A4). .For every vector Y there exists a vector −Y, such that Y+(−Y)=0. | ||
| B. | . .For all vectors Y, Z and scalars α, β, | |
| (B1). .1•Y=Y | (B2). .α(βY)=(αβ)Y | |
| (B3). .(α+β)Y=αY+βY | (B4). .α(Y+Z)=αY+αZ | |
. . Therefore the ordered set is a vector. The author defines it as the vector which is termed a vector of the second kind, or a point. Although it should be expressed vertically in brackets, it may be expressed horizontally in parentheses to save space.
. . The vector defined above has the properties and quantities different from such well-known vectors as force, velocity, acceleration, except of above mentioned addition and subtraction of vectors and multiplication of vectors by scalars. The concepts for the magnitude, inner product and outer product of the well-known vectors are not used here because these have not the senses of the magnitude and product of the function expressed in the ordered sets. The magnitude and product of the ordered set will be defined afterwards. Accordingly, when "vector" is not preceded or followed by a descriptive word or phrase such as "usual", it is used in the sense of the above ordered set here-after.
1.2 Some properties of the vector space.
. .
There exist the p+1 vectors expressed in the ordered sets whose only one member is not zero and equivalent to respective member of the ordered set Y0 as represented in Eqs.(1.4). The linear combination is expressed in Eq.(1.5), where α0, α1, α2, ……, αp are scalars. It is zero by the definition of zero vector, only if the coefficients are all zero. Hence the p+1 vectors are linearly independent and the vector space is the p+1 dimensional space. The vector Y0 is a point in the space and the linear combination of the p+1 vectors with all the coefficients of one. The p+1 vectors are the components of the vector Y0.
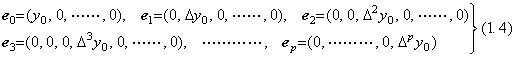
. . The p+1 vectors in Eqs.(1.4) represent the function expressed in Eqs.(1.6) so the magnitudes are respectively defined by the norms in Eqs.(1.7). Therefore the norm of the resultant vector Y0 is defined by Eq.(1.8).
. . These definitions evidently hold the following properties of normed space, where Y and Z are arbitrary vectors in the space and α is any scalar.
| (N1) | ||Y || ≥0 | (N2) | ||Y ||=0. . ⇔ . .Y =0 |
| (N3) | ||αY ||=|α|•||Y || | (N4) | ||Y+Z || ≤ ||Y ||+||Z || |
. . In this space, the vector (c, 0, 0, …… , 0) denotes a constant function and the vector (y0, Δy0, 0, …… , 0) denotes a linear function and the vector (y0, Δy0, Δ2y0, 0, …… , 0) denotes a quadratic function. These vectors are not changed, even if they are appended any number of members with the value zero at the tails. If the function is y=2t for t=nh, the members with the values (2h−1)p+k for k=1, 2, …… , must be appended, because the members up to (p+1)th are,
Hence the vector is changed by the dimension of the space. These are similar to the relation between definite decimal and indefinite decimal.
. . If all the members after (p+1)th are truncated, the vector in the p+k+1 dimensional space is projected to the p+1 dimensional subspace in orthogonal because the p+1 components exist in the subspace. If the remainder term of Newton's interpolation formula is not negligible, the projected vector has significant difference from the original vector. However, if a sequence of vectors is continuous in the p+k+1 dimensional space, the sequence of the vectors projected to the p+1 dimensional subspace is also continuous. It is evident by the orthogonal projection of a locus in the three dimensional Euclidean space to two-dimensional subspace.
. . Therefore it is able to operate all the vectors as that they exist in the same dimensional space. Accordingly, it must be remembered that the sequence of vectors converges to the orthogonal projection of the true limit to the p+1 dimensional subspace, if it converges. Hence if the limit y(t) is expressed in Newton's interpolation formula with the remainder term which is not negligible, the sequence of functions converges to the slightly different function from the limit y(t). This is the reason why the usual iterative method solving differential equations such as Milne's method converges to the slightly different value from the accurate solution, if the interval h is not enough small.
1.3 The finite differences of vectors.
. .
The author defines the finite difference of vectors as the subtraction of the two vectors Y0, Y1 which are the vectors of a function y(t) at t0 and t1=t0+h respectively. It is expressed in Eq.(1.9) and equivalent to the vector of the subtracted function Δy(t)=y(t+h)−y(t) at t=t0. It is denoted by ΔY0 because it is equivalent to the vector whose members are the product of Δ and the members of the vector Y0 and because the first member is Δy0.
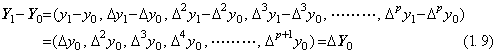
. . The vector Y0 has the member Δp+1y0 because it is defined on the interval [t0, tp+1] so it exists in the p+2 dimensional space. On the other hand, the vector Y1 has not Δp+1y1 on the interval so it exists in the p+1 dimensional subspace. Hence the above subtraction must be carried out by use of the vector which is the orthogonal projection of Y0 to the p+1 dimensional subspace. The projection of Y0 may be also denoted by Y0, if there is no danger of confusion, because the last member is truncated only.
. . The difference ΔY0 is the orthogonal projection of Y0 to the p+1 dimensional subspace which consists of the second to (p+2)th coordinates. The projection is called the operation Δ for Y0 truncated the last member. Therefore the operation Δ is the mapping of the first p+1 dimensional subspace into the second p+1 dimensional subspace. Because the vectors in the both subspaces are the projections of the vector Y0 in the p+2 dimensional space, y0 is not unknown so the operation Δ is reversible, that is, ΔΔ−1=Δ−1Δ=1.
. . The operation Δ is equivalent to the operation which shifts all the members of the ordered set in Eq.(1.1) to the left by one cell with the result that the first member of Y0 has been removed and Δp+1y0 appears in the last cell after the shift. Therefore if there is such a vector as (1, 2, 3, …… , 0), it must be noted that the operation Δ obtains (2, 3, …… , 0) whose first member is the value on the second coordinate.
. . If the function is y(t) on the interval [t0, tp+k], the vectors Y0, Y1, Y2, …… , Yk exist respectively at the equidistant points t0, t1, t2, …… , tk. Accordingly, these vectors are the value of the function Y(t) at these equidistant points and the k-th differences is defined as follows.
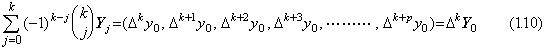
. . The vector ΔkY0 is equivalent to the function expressed in Eq.(1.11) and it is the orthogonal projection of Y0 to the last p+1 dimensional subspace which consists of the (k+1)th to (p+k+1)th coordinates. The operation Δk is the mapping of the first p+1 dimensional subspace into the last p+1 dimensional subspace. The inverse vector of ΔkY0 is the orthogonal projection of Y0 to the first p+1 dimensional subspace. Hence the operation Δk is reversible.
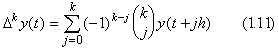
1.4 The product of vectors.
. .
The author defines the product of two vectors Y, Z as the vector W which is the vector of the product of the two function w(t)=y(t)z(t) and he expresses it in W=YZ.
. .
[Theorem 1.1]. .Letting the values of three functions be denoted by y0, y1, y2, …… , yp and z0,
z1, z2, …… , zp and w0, w1, w2, …… , wp for equidistant points t0, t1, t2, …… , tp, the product of the vectors W=YZ is expressed in the matrix equation Eq.(1.12).
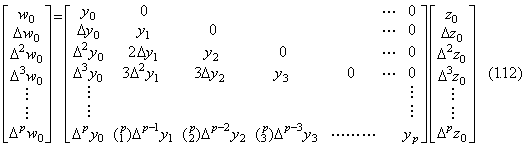
. . [Proof]. .The proof of the each row is given by the finite differences of wk=ykzk as follows.
1). .w0=y0z0.. .Hence the first row has been proved.
2). .
. 
. . On the second terms,
. Therefore,
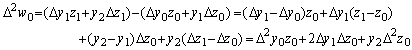
Hence the 3rd row has been proved.
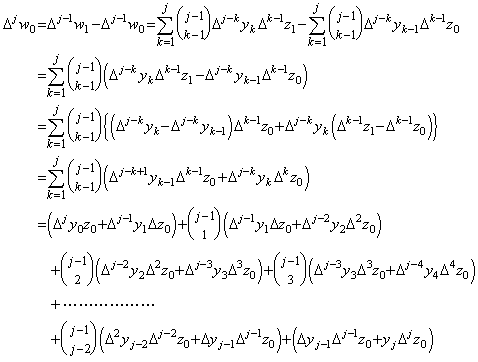
. . Associating the right term in every paired parentheses with the left term in the next after parentheses, for the values of k=1 to j−1,
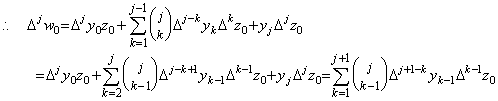
Therefore the (j+1)th row has been proved.________[Q.E.D]
. . The matrix in Eq.(1.12) is obtained by following method. The values yk−1 of the function are placed on the diagonal k-th cell and the values 0 are placed on all the right cells of the diagonal. After the difference table has been constructed on the left cells of the diagonal in such a way that the cell in the j-th row k-th column (k<j) has the difference of the value in the j-th row (k+1)th column by the value in the (j−1)th row k-th column, the value in the j-th row k-th column is multiplied by the binomial coefficient
. Hence the first column of the matrix consists of the vector Y.. . In case of the operational calculus which are carried out by vectors, the matrix is obtained by following method. The vector Y is placed on the first column of the matrix and after the difference table has been constructed on the right cells in such a way that the cell in the j-th row k-th column (1<k≤j) has the sum of the value in the (j−1)th row (k−1)th column and the value in the j-th row (k−1)th column, the value in the j-th row k-th column is multiplied by the binomial coefficient
.. . This matrix is denoted by the type which is of the same one as the vector but not bold-faced. So the product of the vectors are expressed in Eq.(1.13). Because of (Y−Y)Z=0 for any Z≠0, the matrix Y is equivalent to the vector Y. The author names the matrix as the expansion of a vector.
. .
[Theorem 1.2]. .All vectors W, Y, Z hold following properties.
| (1) | YZ=ZY | (2) | (YZ)W=Y(ZW) | (3) | W(Y+Z)=WY+WZ |
. . [Proof]. .(1)__ y(t)z(t)=z(t)y(t)___∴ YZ=ZY___∴ YZ=ZY
(2). .{y(t)z(t)}w(t)=y(t){z(t)w(t)}___∴ (YZ)W=Y(ZW)___∴ (YZ)W=Y(ZW)
(3). .w(t){y(t)+z(t)}=w(t)y(t)+w(t)z(t)___∴ W(Y+Z)=WY+WZ___∴ W(Y+Z)=WY+WZ
| [Q.E.D] |
. . In the commutative law, it must be noted that the left vector is always expanded into the matrix when the multiplication of vectors is expressed in Eq.(1.12) for the execution. On the other hand, if it needs to change the order of the matrix and the following vector in Eq.(1.12), they must be transposed by the reversal law of product of matrices.
. . The multiplication of any vector by a scalar cY is able to be expressed in the product of the diagonal matrix, which has the constants c on the principal diagonal, and the vector Y. The diagonal matrix is equivalent to the matrix which is the expansion of the vector C=(c, 0, 0, ……) denoting the constant function. Hence it is able to express the product cY in the product of vectors CY. That is, in this operational calculus, it does not need to distinguish scalars from constant vectors. Accordingly, the author does not use the concept of the multiplication of a vector by a scalar hereafter.
. . However, he will use the expression cY, if he would like apparently to show that the vector C is a constant or a constant function. In the case, the expression c denotes the matrix into which the vector C is expanded. So it will also be used when it denotes any matrix.
. . Letting the vector 1 denote the vector (1, 0, ……, 0), any constant vector can be denoted by c1. It will be used in order to denote the initial value by y01 when the solution of a differential equation is expressed in the matrix equation, because it is not able to distinguish the denotation of the constant vector (y0, 0, 0, ……) by the rule from the vector Y0 in Eq.(1.1).
. . Letting Z=1 be substituted in Eq.(1.12), any vector Y is expressed in Y=Y1. Hence the author names the vector 1 as the unit vector. Because of Y1=1Y, it is able to expand the vector 1 into the unit matrix.
. .
[Theorem 1.3]. .Letting W=YZ, the matrices W, Y, Z into which the vectors are expanded, hold the equality W=YZ.
[Proof]. .Letting the matrix C be the product of Y and Z, it is shown that the matrix C is equivalent to the matrix W into which the vector W is expanded.
. .
Letting C,Y,Z be expressed in the elements cjk, ajm, bmk, ( j, k, m≥1) respectively, the elements
ajm are all zero for m>j and the elements bmk are all zero for m<k. Hence the matrix C is the triangular matrix which has zero in all the cells of k>j because of m>j for m≥k in case of multiplying ajm by bmk. In case of k≤j, letting the values of the functions for the vectors W, Y, Z be denoted respectively by wj−1, ym−1, zk−1,
. . In case of k=1, the right side of Eq.(1.14) is equivalent to the j-th element of the product YZ by Theorem 1.1, so the element cj1 is equal to the element in the j-th row first column of the matrix W.
. . In case of k≥2, the proof is given by the every group which consists of the members on the every line running parallel with the principal diagonal.
| 1) | . .In case of k=j, because of m=j only, Eq.(1.14) comes to cjj=yj−1zj−1=wj−1. It is equal to the j-th element in the principal diagonal of the matrix W. | ||
| 2) | . .In case of k=j−1, because of m=j−1=k and m=j=k+1,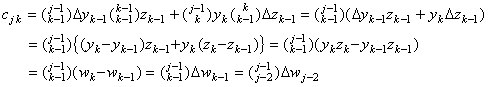 It is equal to the left element of the principal diagonal of the matrix W. | ||
| 3) | . .In case of k=j−2, because of m=k, k+1, k+2, where, 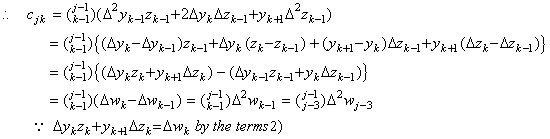 and k+1=j−1 Hence cjk is equal to the j-th row (j−2)th column of the matrix W. | ||
| 4) | . .In case of k=j−n, assuming that cjk is equal to j-th row k-th column of the matrix W, . .In case of k=j−(n+1), the values m are m=k+u for u=0 to n+1 and,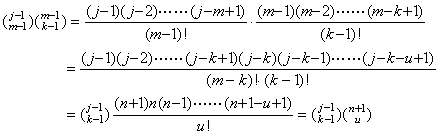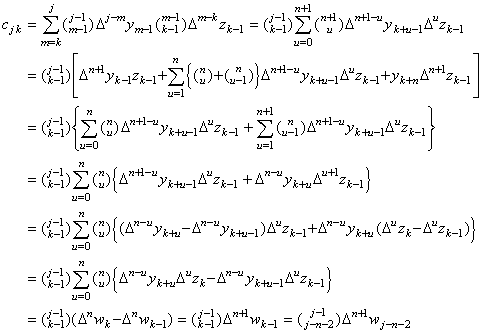  
|
. . Although the product of vectors YZ is commutative, if the vector Y is expanded into the matrix Y, the product YZ is not commutative. However, if the both vectors are expanded into the matrices, the product YZ is commutative. It is easily proved by interchanging the denotation y and the denotation z in the proof of Theorem 1.3. These show that the matrix into which the vector is expanded is equivalent to the vector except that it expresses more properties and quantities of the vector explicitly. The relation between the two is similar to the relation between fractions and decimals.
1.5 The quotient of vectors.
. .
When the equality W=YZ is satisfied, the author defines the multiplicand or the vector Y as the quotient of the vector W by the vector Z and expresses it in the equality Y=W/Z. The vector W may be expressed in the equality W=ZY by Theorem 1.2. In the case, the vector Z is the quotient of the vector W by the vector Y and expressed in the equality Z=W/Y. If the quotient 1/Y is a vector, the author names it as the reciprocal vector of Y and also expresses the vector Z in the equality Z=W(1/Y)=(1/Y)W. He will also denote the reciprocal vector as Y−1 and names it as the inverse quotient, when it is used in the operation Z=Y−1W which is the inverse operation of W=YZ.
. .
If a value yk of the function y(t) is not zero, there exists a value zk expressed in zk=wk/yk which is the value of the function z(t)=w(t)/y(t) at t=tk. If all the values z0 to zp exist for the equidistant points t0, t1, t2, ……, tp by an interval h, the vector Z which consists of the finite differences is the quotient of the vector W by the vector Y. The quotient Z is also obtained by the product of the vector W and the vector which consists of the finite differences of 1/y0 to 1/yp, because of zk=wk(1/yk). The reciprocal vector Y−1 is the vector which consists of the finite differences of 1/yk. Accordingly the necessary and sufficient condition on which there exist a quotient and a reciprocal vector is det(Y)≠0, where det(Y) denotes the determinant of the matrix Y into which the vector Y is expanded, because the condition is that the matrix has not zero on the principal diagonal.
. .
[Theorem 1.4]. .The reciprocal vector Y−1 is unique and its elements are expressed below, where Y1k denotes the cofactor of the element in the first row k-th column in the determinant of the matrix Y into which the vector Y is expanded and det(Y) denotes the determinant of the matrix Y.
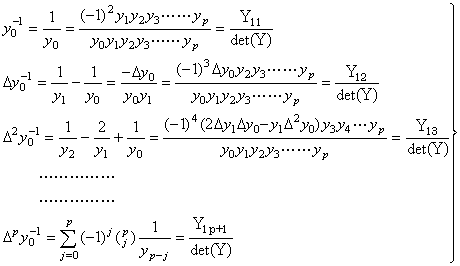(1.15)[Proof]. .Because det(Y)≠0 by all the diagonal elements yk≠0, the inverse matrix Y−1 exists uniquely. Let Z denote the vector which consists of the finite differences of 1/yk.
Because of yk(1/yk)=1,
| YZ=1 | ∴. .YZ=1 | ∴. .Z=Y−11 |
. .
[Theorem 1.5]. . The matrix into which the reciprocal vector Y−1 is expanded is the inverse matrix of the matrix Y into which the vector Y is expanded.
[Proof]. . Because of det(Y)≠0, the inverse matrix Y−1 exists uniquely. Let Z denote the matrix into which the reciprocal vector Y−1 is expanded. Because of YY−1=1 and Theorem 1.3,
| YZ=1 | ∴. .Z=Y−1 | [Q.E.D.] |
1.6 The expanded definition of the quotient of vectors.
. .
If a value of function yk is zero, there are not any quotient by the vector Y and the reciprocal vector Y−1, because it is impossible to calculate the finite differences at 1/yk=∞. It may occur if the function y(t) intersects the t-axis in the range [t0, tp]. However, if we place restriction on the range so that it does not include the intersecting point or adjust the interval h between equidistant points to such a value that any equidistant point is not equal to the intersecting point, it follows that the quotient by the vector and the reciprocal vector exist. It is inconvenient that the vector Y of a function in the range [t0, tp] changes the property as to the existence of the quotient by Y according to the value of equidistant interval. So the author expands the definition of the quotient so that they always exist in such case.
. .
When a value of function yk is equal to zero, the product wk=zkyk is zero uniquely so the vector W is determined uniquely by the equation W=ZY. In the case, the author defines that the quotient Z exists uniquely, and expresses it in Z=W/Y. By the definition, there exists a quotient if the vector Y is not zero, even if det(Y) is zero for the matrix Y into which the vector Y is expanded. Hence the quotient has become similar to the quotient of numbers but the reciprocal vector of Y does not exist because of wk=zk×0≠1, whereas the product W must be the unit vector 1 for existence of the reciprocal vector. However, it is able to admit expressing the quotient in the multiplication by 1/Y or Y−1, because Y/Y=1 is held by the definition of quotient Y=1Y even if det(Y) is zero. Hence,
. . The formula using the expanded quotient of vectors may be changed by use of ZY=W or Y/Y=1. Also it is able to construct the vector of the differences of zn=wn/yn, if the value zk are known at the point tk where the values wk, yk are zero. If it is unknown, the quotient Z is indefinite because the value zk=0/0 is indefinite. That is, the expanded quotient means the original vector Z which was converted into the vector W expressed in W=ZY but it does not mean the quotient of any two vector W/Y. Therefore the expanded quotient is unique and it is able to admit expressing it in Z=Y−1W, which is the inverse operation of W=YZ. So the denotation Y−1 is the inverse quotient but not the reciprocal vector. The uniqueness of the expanded quotient is similar to the differential equation, which has the unique solution when the initial value is known.
. . When det(Y)=0, it is well known that the simultaneous equations YZ=0 have a solution being not zero. If it is denoted as Za,
| W=Y(Z+Za)=Y(Z+Za)=(Z+Za)Y | (1.16) |
. . If yk=0 for a point tk, the value wk=(zk+za)yk is zero for any za. If the equidistant interval h is changed for such a value that the point tk is shifted by infinitesimal value ε from the point ta on which the function y(t) intersects the t-axis, the value za must become zero because zk=wk/yk become unique. Hence the function za(t) is zero everywhere except at ta, where za(t) is indefinite, that is, za(t) and z(t)+za(t) are not continuous at tk, if tk=ta and za(ta)≠0. If za(ta)=0, Eq.(1.16) has only the vector Z as the quotient W/Y. The condition is satisfied, if and only if the value z(tk) is known.
. . Therefore the author's operational calculus requires for the functions to be continuous when it uses the expanded quotient. It is possible for the tabulated functions to satisfy the requirement if they can be expressed in Newton's interpolation formulas, which are the transformation of the tabulated functions into the continuous functions. Accordingly, if Y≠0 and YZ=0 in these functions, the quotient 0/Y is only Z=0 and if Y=0, there exist no quotient because it has no meaning to obtain the function whose values zk are all known. So it is not admitted to divide any vector by the vector 0. Further if YZ=0, either the vector Y or Z is zero at least.
. .
[Theorem 1.6]. .The quotient or expanded quotient Z=W/Y is expressed in the following matrix equation.
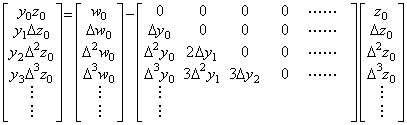. .(1.17)| [Proof] | W=ZY=YZ=YZ | ∴ | YZ=W |
. .
Although the elements of the vector Z exist in the both side of Eq.(1.17), they are easily obtained by iterative technique as follows.
| 1) | The first row in Eq.(1.17) gives y0z0=w0. Hence z0=w0/y0. |
| 2) | Substituting it into the right side Z, the second row gives, |
| 3) | Substituting it into the right side Z, the third row gives, |
| 4) | In a similar way,  |
| 5) | Other higher order differences are all obtained in a similar way. |
. . If the value y2 is zero, the value z2 must be given and the value Δ2z0 must be calculated by use of z0, Δz0 obtained above and the given z2 instead of above step 3. In the case, the value Δ2z0 may be known instead of z2 and if so, the above step 3 may only be skipped.
1.7 The vector-valued functions.
. .
When there is a continuous function y(t), there exist the vectors Y0, Y1, Y2, …… whose first components are y(t0), y(t1), y(t2), …… respectively, where the points tk are equidistant by tk=t0+kh. Further there exist continuously the vector Y whose first component is y(t) for any point t. If the first point is denoted as x0, the equidistant points of the case are expressed in xk=x0+kh for k=0, 1, 2, ……, p. Hence they are expressed in the following vector with p+1 components. The vector Y also has the same number of components.
| X=(x0, h, 0, ……, 0) | (1.18) |
. . Therefore the vector Y is able to be denoted as Y(X) and the author names it the vector-valued function. The function Y(X) is easily obtained by replacing the vectors Y and X for the respective denotation y and t of the function y(t). For example,
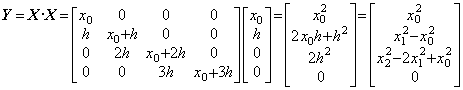. .(1.19)The components of the resultant vector are equal to the finite differences of y(t)=t2 for the equidistant points x0, x1, x2, ……. Hence the vector-valued function is expressed in,
| Y=Y(X)=X 2 | (1.20) |
. . The rational functions are also transformed into the vector-valued functions by replacing the vector-valued variable X for the variable t. The vector value of the function is obtained by the expanded quotient of the two vector-valued functions in numerator and denominator. It is the same with the irrational functions but the vector value should be obtained by the finite differences of the irrational function. It may also be obtained by Taylor's expansion expressed in the power series of the vector X. However, it needs to be careful about the accuracy of the components because the expansion does not always hold that the remainder terms are zero at the equidistant points.
. . When there is a function Y=F(X), there exists the function which gives the vector X for the vector Y inversely. It is called the inverse function and expressed in X=F −1(Y). The inverse function is unique because the equidistant interval h must be of the same with the function Y=F(X). Therefore, if the value h is positive, the inverse function of Eq.(1.20) is,
. .(1.21). . There are the two numbers n and −n whose squares come to n2, so the square root of n2 is not unique. In case of the function y=t2, the value y does not correspond with the value t by one-to-one. However, the point on the locus corresponds with the point on the t-axis by one-to-one as explained in Fig.1. In a similar way, the vector is the graphical quantity which consists of the magnitude and direction, and the vector at p1 is not equal to the vector at p0, although the difference is not represented in Eq.(1.20) explicitly.
. .
The vector X at t=x0 is expressed in Eq.(1.18) but at t=−x0, it is,
| X−=(−x0, h, 0, ……, 0) | (1.22) |
The vector value of the function F for it is different from the vector value for X in the respect that it has the negative second component because the absolute value |x1|=|−x0+h| is less than the absolute value |−x0| in Eq.(1.19). On the other hand, the vector −X is symmetrical transformation of the vector X and the square comes to the same with Eq.(1.20). It has the same components with the vector value of the function F for the vector X . However, the vector Y at p1 has the equidistant points running backward, that is, it has the negative equidistant interval because the vector −X is,
| −X=(−x0, −h, 0, ……, 0) | (1.23) |
. . Therefore, when the function with respect to X is expressed in Eq.(1.20), the inverse function must hold the equidistant interval h and it is expressed in Eq.(1.21) uniquely, if h>0. It is similar to the existence of the unique solution by known initial value in case of differential equations.
. . In case of h<0, the vector X and Y are constructed by the backward differences so the inverse function comes to,
. .(1.24)Hence the condition h may be replaced by the condition whether the vector X is positive or not. The quadratic function may be expressed in Y=(−X)2, if we will explicitly express that it has the inverse function in Eq.(1.24).
. . The vector value of the square root of Y may be obtained by use of Taylor's expansion of Eq.(1.21) or the finite differences of the square roots of y0, y1, y2, ……, yp. It can also be obtained by the vector calculation using the Newton-Raphson's method. The program and results are mentioned in Chapter 4 section 1.6 and section 3.2.
1.8 The absolute value of the vector.
. .
The condition on which the vector
exists is that all the values
exist. Hence the conditions yk≥0 must be satisfied for all the values k in the range where the vector Y is defined. In the case, it can not always be judged immediately from the signs of the components whether all the values yk satisfy the condition or not, because the signs except of the first component depend on the form of the function. It needs to check the signs of all the principal diagonal elements of the matrix into which the vector Y is expanded. If the every diagonal element is greater than or equal to zero, the square root of Y exists.
. .
Therefore the author defines the case as Y≥0. If all the diagonal elements are less than zero, he defines the case as Y<0. Accordingly, it is necessary to remember that there exists the vector which is not positive and not zero and not negative. Such vector denotes that the function y(t) intersects with t-axis in the range where the vector is defined. The vector vanishes in the case when the equidistant interval becomes the limit h→0.
. .
The absolute value of a vector must be defined as the vector value which is positive or zero. The absolute value of a function |y(t)| are also a function with respect to t and there exists the vector into which the function is transformed. The author defines the vector as the absolute value of the vector Y and denotes it as |Y|. This operational calculus does not use the usual concept of the absolute value for a vector, because it has not this sense.
. .
If the vector |Y| is expanded into the matrix, the principal diagonal elements are the absolute values of the function |yk| by the definition and the other elements are constructed by the expanding method mentioned in section 1.4. The first column is the vector |Y| and the first component of the vector |Y| is positive because of |y0| but it depends on the form of the function
. .
The vector whose components are the absolute values of the components of a vector Y is positive. However, the relation between it and |Y| is expressed in Eq.(1.25).
. .[Theorem 1.7]. . | (1.25) |
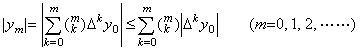_____[Q.E.D.]. . In usual vector, the absolute value is the magnitude of the vector. However, it does not represent the magnitude in this operational calculus and represents the absolute valued function. Accordingly, when there are any two vectors Y, Z, it can not always be judged by Y−Z or |Y|−|Z| which vector is greater, except for the case that they satisfy a particular condition as in Theorem 1.7. It must be judged by the norms of the functions. It is the reason why the magnitude of a vector is defined by the norm of the function.
. . The norm of a function may usually be greater than the absolute value of the function at any equidistant point. However, if the equidistant interval is enough small, it will be recognizable that the norm will become equivalent to the absolute value of the function at some equidistant point within given accuracy. Hence the norm of a vector may be defined as the maximum absolute value on the principal diagonal of the matrix which is the expansion of the vector. Accordingly, it is judged by expanding two vectors into the matrices which vector is greater.