4.2 The numerical solution of closed-loop systems.
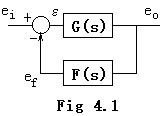
Fig4.1 . . The automatic controller usually is the closed-loop feedback system whose output is fed back to the input so as to affect the output. The block diagram is represented in as Fig 4.1. In general, the transfer functions G(s) and F(s) take the form expressed in Eq.(4.3) and Eq.(4.4) respectively. The relation between output and input is expressed in Eq.(4.5), using the closed-loop transfer function. Hence the relation may be simulated by the numerical simulator transforming the transfer function into the differential equation mentioned in section 3.

Eq4_3Eq4_4
Eq4_5
. . However, it is more simple and better to solve the system of two differential equations transformed from the transfer functions G(s) and F(s) respectively, because all the values eo, ef, ε are obtained at the same time and it does not need to obtain the closed-loop transfer function. The differential equations come to Eqs.(4.6) with all the initial values of zero because all the signals are ei=ei(t)u(t), eo=eo(t)u(t) and ef=ef(t)u(t).
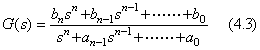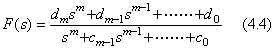. . In order to solve the system of the differential equations, the unit step functions may be removed without any change of the form of the differential equations. However, the initial values must be changed for the values which are determined by the coefficients of the subsidiary variable s in the numerator and denominator of the transfer functions and the solution must be multiplied by u(t) as mentioned in section 3.6.
Eq4_6
. . When all the unit step functions are removed, the initial values of eo(t), ef(t) and these derivatives are determined by following matrix equations, where ei, eo, ef and these derivatives denote the initial values simply.
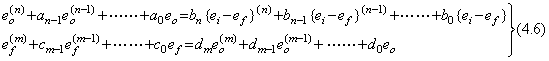
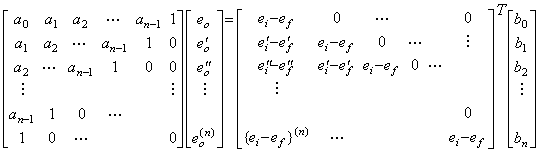
Eq4_6a
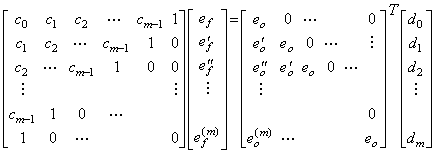
Eq4_6b
. . In order to eliminate the calculation of these initial values, the transfer functions may be divided into two parts of the numerator and the denominator as shown in Fig 4.2. In case of open-loop system and closed-loop transfer function, the output eo may be obtained by summing the solution e and derivatives of the differential equation only at the edge of the interval by one step of the numerical solution of differential equations, as mentioned in section 3.11.
Fig4_2
. . However, in case of closed-loop system, the results of the numerator must be calculated at the every point used by the one step of the numerical solution of differential equations. Accordingly, the system of the differential equations has the four variables e, eo, f, ef. However, in order to use the numerical simulator mentioned in Section 3 and Program 4.1 as the solution of the system of differential equations, it is more simple to calculate eo and ef only at the edge of one step and to change the system of differential equations to such system that have two variables e and f. Therefore the numerator on the forward path must be expressed in the function driving the differential equation of the transfer function on the feedback path and the numerator on the feedback path must be expressed in the differential equation on the forward path as shown in Eqs.(4.7).
Eq4_7
. . The denotation e and f are also e=e(t)u(t) and f=f(t)u(t) and the unit step functions are removable without any change of the form of the differential equations and the initial values. In the case, the initial values of the system of differential equations in Eqs.(4.7) are all zero except the case of impulsive response. The indicial response has the value ei=1 and all the initial values of zero. The impulsive response has the value ei=0 and the initial value e(n−1)=1, which are equivalent to the impulse function δ(t). In this case, if the value bn is not zero, the initial value of f(m−1) must be the value bn because the differential equation on the feedback path is driven by the output eo having the additional impulse function bnδ(t) which is added to the solution of the homogenous differential equation on the forward path, mentioned in section 3.6. Furthermore, if the value dm also is not zero, the feedback signal ef has the additional impulse function dmbnδ(t) and the differential equation on the forward path is driven by the difference of the input impulse and the feedback impulse. Hence the results are as follows.
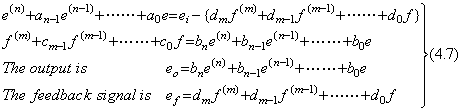
. . Assuming eo=kδ+……, the feedback signal is ef=dmkδ+……. Therefore,
Eq4_8

The result is also obtained by the closed-loop transfer function as follows.
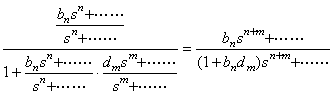
Eq4_8a
This comes to the result that the differential equations on the forward path and feedback path are respectively driven by,
Eq4_9 Eq4_10
. . Therefore, in case of bn≠0 and dm≠0 in Eqs.(4.7), the differential equations of the impulsive response become respectively the homogeneous differential equations with the initial values in Eq.(4.11). And the solutions eo and ef must be respectively appended kδ and dmkδ, where k is the value in Eq.(4.8).
Eq4_11
. . For example of bn≠0 and dm≠0, assuming that G(s) and F(s) are first-order transfer functions as follows,
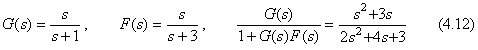
Eq4_12
The impulsive response is,
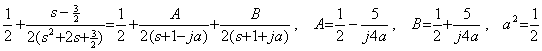
Eq4_12a
Therefore,
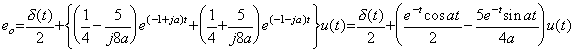Eq4_13. .(4.13)
The feedback signal is,
Eq4_13a
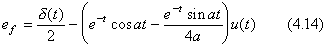
Eq4_14
. . The above closed-loop system is expressed in the system of two differential equations by Eqs.(4.6) as follows.
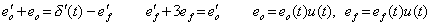Eq4_15_____(4.15)
Eliminating ef' and ef from the first equation,
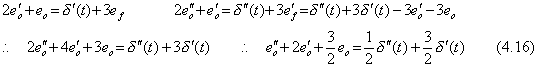
Eq4_16
Transforming the right side function to the initial values by Eq.(3.38) in Section 3.6, the homogeneous differential equation is obtained as follows.
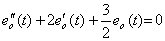Eq4_17_________(4.17)
The initial values are obtained as follows.
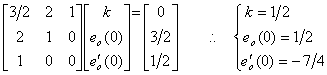Eq4_18______(4.18)
Therefore, the solution is,
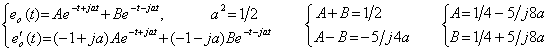
Eq4_18a
Multiplying eo(t) by u(t) and adding kδ(t)= δ(t)/2, the result is same as Eq.(4.13).
. . In order to eliminate the estimation of the initial values of the homogeneous differential equation in Eq.(4.17), the differential equation in Eq.(4.16) is transformed as,
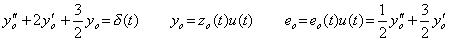Eq4_19___(4.19)
Removing u(t) and δ(t), this is equivalent to,
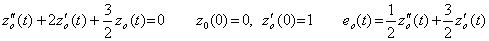Eq4_20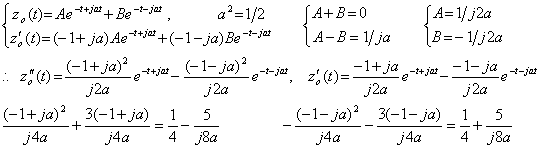___(4.20)
The solution is same as above result because of followings.
Eq4_20a
In the same way, eliminating eo' and eo from the second equation of Eq.(4.15), the solution in Eq.(4.14) is obtained.
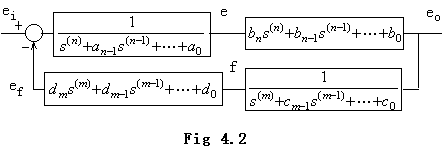
. . The transfer functions G(s) and F(s) in Eq.(4.12) may be separated into the two parts of numerator and denominator as Fig. 4.2, in order to eliminate the estimation of initial values. In the case, the differential equation in Eq.(4.15) is transformed as follows.
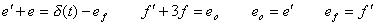Eq4_21____(4.21)
The system of four differential equations is changed to the system of two differential equations by substituting f ' for ef and e' for eo as mentioned in Eq.(4.7).
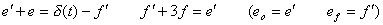Eq4_22____(4.22)
The functions e and f are e=e(t)u(t) and f=f(t)u(t). If there exists no impulse function, the unit step function u(t) can be removed without changing the form of differential equations and all the initial values are zero. However, there exists the impulse function so it must be transformed into the initial value. If the functions f ' and f are eliminated before removing the unit step function, it is same as solving the homogeneous differential equation in Eq.(4.17). If the unit step function is removed before the functions f ' and f are eliminated, the value to which the impulse function is transformed is not one. The function ef has the impulse function δ(t)/2 by Eq.(4.10). It is not expressed explicitly and it is eliminated together with ef or f ' when ef or f ' is eliminated. Accordingly, the impulse function is transformed into one as the initial value. In case that the unit step function is removed before the functions f ' and f are eliminated, the impulse function which the function ef has implicitly must be subtracted. In the same way, the impulse function which the function eo has implicitly must be added to the function driving the differential equation on the feedback loop. Hence, the initial values are determined by Eq.(4.11) respectively and the differential equation in Eq.(4.22) is transformed as follows.
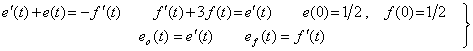Eq4_23____(4.23)
Eliminating f ' (t) and f(t),
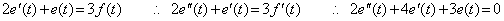
Eq4_23a
Substituting the initial values for the first equation, the initial value e' (0)=1/2 is obtained. Hence, the solution is obtained as follows.
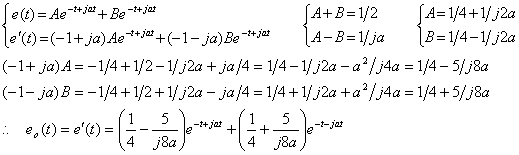
Eq4_23b
Hence, eo=eo(t)u(t)+δ(t)/2 becomes Eq.(4.13). In the same way, eliminating e' (t) and e(t) from Eq.(4.23), the solution ef in Eq.(4.14) is obtained.
. . In order to solve Eqs.(4.7) by the numerical solution of the system of differential equations mentioned in section 4.1, the highest order derivative of the every differential equation must be expressed in the equation of the lower order derivatives. If F1 and F2 are respectively used in substitution for e(n) and f(m), Eqs.(4.7) are represented in Eqs.(4.25). Therefore F1 and F2 must be given the solutions of the simultaneous equations, which are expressed in Eqs.(4.26). Eqs.(4.26) also shows that the initial values come to Eqs.(4.11) in case of ei=δ(t).
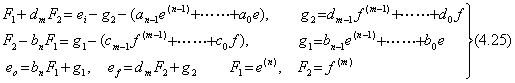
Eq4_25
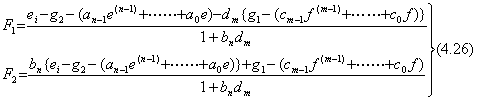
Eq4_26
. . If there are many transfer functions on the forward path and feedback path, these transfer functions may be transformed into the differential equations respectively. If the differential equations consist of such simultaneous equations with many unknown F1, F2, ……, the program solving the system of differential equations may be given the subroutine which obtains the solutions F1, F2, …… of the simultaneous equations.

4.3 The numerical simulator of closed-loop systems.
. . The numerical solutions of closed-loop systems may be obtained by use of Program 4.1 which obtains the solutions of the system of differential equations. However, the program must be slightly changed as shown in bold-faced type in Program 4.2, because the system has the additional equations equivalent to the numerators of the transfer functions as shown in Eqs.(4.25).
. . Line 10 must be appended the array G(5) which are used for substituting the values g1 and g2 in Eqs.(4.25) into G(1) and G(2) respectively. The variables G(1) and G(2) are also used for the values eo and ef respectively. "GOSUB 60" in Line 40 is placed after "GOSUB 54" which calculates the values g1, g2, F1 and F2 for the solution of the step as the starting values of the next step by use of Line 62. "IF EB<EE THEN RETURN ELSE" at the top of Line 60 is appended to print the solutions only on the points described in Line 64. The variable YY# in Line 60 must be substituted G(J).
. . In Line 66, the values eo and ef must be calculated by use of the values calculated in Line 62 and substituted into G(1) and G(2) respectively, if the values bn and dm are not all zero. If the values bn and dm are both zero, it is not need to calculate the values eo and ef in Line 66 because they are of the same as the values calculated in Line 62. Line 62 may be given Eqs.(4.26) which are the solutions of the simultaneous equations in Eqs.(4.25).
. . The example in Eqs.(4.12) gives the system of differential equations in Eqs.(4.22), so it consists of the simultaneous equations as to e' and f ' in Eqs.(4.27). The solutions are expressed in Eqs.(4.28). Line 62 must give the equations without δ to F(1) and F(2) respectively, where the values e and f are given in Y(1,1) and Y(1,2) respectively by the main program. In this case, G(1) and G(2) is not used in Line 62 because the values g1 and g2 are both zero.

Eq4_27 Eq4_28
. . Line 64 must give the range XB to XE, the number of divisions N, the number of differential equations NF, the order of the respective differential equations ND(1) and ND(2), and the initial values Y(1,1)=e(0) and Y(1,2)=f(0), where e(0) and f(0) are one half because both of Eqs.(4.28) have δ/2.
. . Line 66 gives the accurate values of the solutions, if it needs to compare the accuracy of the solutions. The values eo=e' and ef=f ' must be given to G(1) and G(2) respectively in this example by Eqs.(4.25).
. . Table 4.2 represents the numerical results eo(t), ef(t) of the example. The true solution given by the transfer functions and expressed in eo=eo(t)u(t) and in ef=ef(t)u(t) must be slightly compensated at t≤+0. The values at t=0 are eo(0)=1/2 and ef(0)=−1 by Eq.(4.21) and Eq.(4.28), but the values eo=eo(0)u(0) and ef=ef(0)u(0) are both zero. And the values at t=+0 are eo=eo(+0)u(+0)=1/2 and ef=ef(+0)u(+0)=−1. Furthermore, the impulse function δ(t)/2 must be superposed to the results respectively.

Program 4.2 The simulator of closed-loop systems.
(The other lines are of the same as Program 4.1.)

10 DIM Y0(6,5),Y1(6,5),Y2(6,5),Y(6,5),F(5),G(5),R1(5),R2(5),R3(5),RA(5),ND(5),
. . Y#(5):DEFINT E,J,N
40 GOSUB 44:IF J>NF THEN X=X2:GOSUB 54:GOSUB 60:X0=X2:GOSUB 46 ELSE
. . IF EE<&H4000 THEN EE=EE*2:ES=EB*2-1:EB=EE+1 ELSE PRINT"EE>&h4000":END
60 IF EB<EE THEN RETURN ELSE X#=X2:GOSUB 66:FOR J=1 TO NF:YY#=G(J):PRINT USING
. . " Y(#)=##.#######^^^^ True=##.########^^^^";J;YY#;Y#(J);:NEXT:PRINT:RETURN

62 F(1)=(3*Y(1,2)-Y(1,1))*.5:F(2)=(-3*Y(1,2)-Y(1,1))*.5:RETURN
64 XB=0:XE=50:N=500:NF=2:ND(1)=1:Y(1,1)=.5:ND(2)=1:Y(1,2)=.5:RETURN
66 G(1)=F(1):G(2)=F(2):A#=SQR(.5#):AS#=A#*X#:AC#=COS(AS#):AS#=SIN(AS#)/A#:
. . A#=EXP(-X#):Y#(1)=A#*(.5*AC#-1.25*AS#):Y#(2)=-A#*(AC#-.25*AS#):RETURN

Table 4.2 The results of impulsive response in Eqs.(4.12).
IBEBEEteo(t)Accurateexpef(t)Accurateexp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
32
34
36
38
40
42
44
46
48
50
52
56
60
64
68
72
76
80
84
88
92
96
100		 2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2		 2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2		 0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.2
3.4
3.6
3.8
4.0
4.2
4.4
4.6
4.8
5.0
5.2
5.6
6.0
6.4
6.8
7.2
7.6
8.0
8.4
8.8
9.2
9.6
10.0		 3.3827767
2.0127741
8.6378098
-8.8663399
-8.6725518
-1.4929368
-1.9849297
-2.3607880
-2.6364592
-2.8263611
-2.9434630
-2.9993707
-3.0044180
-2.9677558
-2.8974423
-2.8005326
-2.6831633
-2.5506365
-2.4075003
-2.2576204
-2.1042544
-1.9501172
-1.7974414
-1.6480346
-1.5033334
-1.3644494
-1.2322141
-1.1072179
-9.8984525
-8.8030852
-6.8489045
-5.2019704
-3.8420301
-2.7413853
-1.8687081
-1.1917829
-6.7938468
-3.0248410
-3.4955447
1.4609389
2.6026650
3.5076598
3.3462073
2.7317170
2.0131853
1.3642770
8.5174863
4.8350703
2.3973739
9.1377551
9.9158351
-2.8293309
-4.0879415		 3.38277684
2.01277443
8.63781348
-8.86630893
-8.67254764
-1.49293611
-1.98492897
-2.36078709
-2.63645837
-2.82636041
-2.94346219
-2.99937002
-3.00441736
-2.96775518
-2.89744186
-2.80053206
-2.68316278
-2.55063636
-2.40749996
-2.25762009
-2.10425417
-1.95011708
-1.79744121
-1.64803440
-1.50333339
-1.36444932
-1.23221416
-1.10721790
-9.89845314
-8.80308671
-6.84890494
-5.20197130
-3.84203108
-2.74138653
-1.86870912
-1.19178379
-6.79385556
-3.02484909
-3.49562163
1.46093238
2.60265935
3.50765597
3.34620512
2.73171595
2.01318500
1.36427691
8.51748748
4.83507218
2.39737582
9.13777214
9.91596499
-2.82932109
-4.08793504		 -01
-01
-02
-03
-02
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-02
-02
-02
-02
-02
-02
-02
-02
-03
-03
-04
-03
-03
-03
-03
-03
-03
-03
-04
-04
-04
-05
-06
-05
-05		 -8.7997419
-7.6975685
-6.6906661
-5.7754374
-4.9476907
-4.2028081
-3.5358837
-2.9418409
-2.4155346
-1.9518331
-1.5456839
-1.1921692
-8.8654846
-6.2428981
-4.0109359
-2.1290988
-5.5947155
7.3322579
1.7816417
2.6158214
3.2632709
3.7490472
4.0958643
4.3241985
4.4524271
4.4969566
4.4723529
4.3914836
4.2656440
4.1046955
3.7104812
3.2636534
2.8035451
2.3571745
1.9419763
1.5681034
1.2403297
9.5958496
7.2417832
5.3074714
3.7497010
1.5733159
3.4059049
-2.6846980
-4.9865741
-5.2132580
-4.4707864
-3.4130926
-2.3850615
-1.5368591
-9.0683068
-4.7687146
-2.0644571		 -8.79974176
-7.69756860
-6.69066619
-5.77543702
-4.94769060
-4.20280812
-3.53588365
-2.94184073
-2.41553457
-1.95183314
-1.54568386
-1.19216933
-8.86548581
-6.24290020
-4.01093853
-2.12910154
-5.59474373
7.33224267
1.78163935
2.61581861
3.26326929
3.74904643
4.09586191
4.32419647
4.45242569
4.49695504
4.47235189
4.39148207
4.26564271
4.10469461
3.71048003
3.26365261
2.80354428
2.35717406
1.94197594
1.56810324
1.24032965
9.59584942
7.24178414
5.30747275
3.74970282
1.57331748
3.40591884
-2.68468902
-4.98656819
-5.21325444
-4.47078409
-3.41309132
-2.38506089
-1.53685893
-9.06830829
-4.76871712
-2.06446008		 -01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-02
-02
-02
-02
-03
-03
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-02
-03
-03
-03
-03
-03
-04
-04
-04
-04
-04
-04
-04
-04
-05
-05
-05

Return to CONTENTS