4. The systems of n-th order differential equations.

4.1 The solution of the systems of n-th order differential equations.
. . Usually, n-th order differential equation is solved by substituting a system of n first order differential equations for it. So a system of m equations of n-th order differential equation is substituted a system of m×n first order differential equations. The author's method is able to solve an n-th order differential equation by no substitution. Hence it is able to solve a system of m equations of n-th order differential equation by no substitution.
. . A system of n-th order differential equations is expressed in Eqs.(4.1), where the values n may be n1 to nm and the exciting functions may be z1(t) to zm(t) respectively. If the initial values are given for y1(t) to ym(t) at t=t0 and these derivatives up to (n−1)th degree, the values from y1(n1)(t0) to ym(nm)(t0) are obtained by Eqs.(4.1). Integrating sequentially these respectively by Euler's method, the values from yk(nk−1)(t0+h) to yk(t0+h) are predicted, where the value k is from 1 to m. Then the values from y1(n1)(t0+h) to ym(nm)(t0+h) are predicted by Eqs.(4.1). These are the midpoint values of the author's 3 points method. In the same way, the values at the midpoint are corrected and the values at t0+2h are predicted and corrected by the author's 3 points method. The values obtained by the second to m-th equation in Eqs.(4.1) are the parameters in order to calculate the right side function f1(t) of the first equation. Hence the first equation is the n1-th order differential equation to be solved and the others are the parts of the right side equation f1. Therefore the system of differential equations in Eqs.(4.1) can be solved by the methods mentioned in above sections, if those are appended the routines calculating these parameters.

Eq4_1

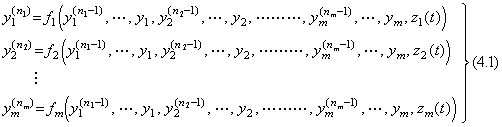
. . The program is represented in Program 4.1, which is the variable pitch method using 3 points. The solutions y1 to ym are the values of Y(1,1) to Y(1,m) respectively and the n-th derivatives y1(n) to ym(n) are Y(n+1,1) to Y(n+1,m). The maximum values of n and m are five in the program but it is able to vary these values by only rewriting the array size if it needs to be done.
. . If the first equation always has the worst condition for existence of solutions, all the solutions y1 to ym have been convergent when the solution y1 has converged. However, it is not always easy to estimate the worst condition previously. In order to eliminate the estimations, Program 4.1 detects that all the solutions y1 to ym have been convergent.
. . The subroutine in line 64 must give the total number of differential equations to NF and the orders of the differential equations to ND(1)∼ND(NF) respectively. Also the initial values of y1∼y1(n−1) to ym∼ym(n−1) must be given to Y(1,1)∼Y(n,1) to Y(1,m)∼Y(n,m). The subroutine in line 62 must give the differential equations to F(1)∼F(NF) in the form expressed in Eqs.(4.1). The line 66 gives the accurate results to Y#(1)∼Y#(NF) if it needs to be done.

Program 4.1 The systems of n-th differential equations.
10 DIM Y0(6,5),Y1(6,5),Y2(6,5),Y(6,5),F(5),R1(5),R2(5),R3(5),RA(5),ND(5),Y#(5):
. . DEFINT E,J,N
12 DEF FNY1=(5*Y0(J3+1,J)+8*Y1(J3+1,J)-Y2(J3+1,J))*H3+Y0(J3,J):
. . DEF FNY2=(Y0(J3+1,J)+4*Y1(J3+1,J)+Y2(J3+1,J))*H4+Y0(J3,J)
14 RP=16777216#:RM=2/RP
16 GOSUB 64:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE;" N=";N;" H=";H0
18 EE=1:XL=XB:X=XB:GOSUB 54:FOR IB=1 TO N:ES=1:XI=XL:XL=XB+H0*IB:X0=XI
20 WHILE 2:H1=H0/EE:EB=ES:WHILE EB=<EE:X2=XI+H1*EB:IF EB=EE THEN X2=XL
22 LOCATE 0,CSRLIN:PRINT"IB=";IB;" EB=";EB;" EE=";EE;" X=";X2;:GOSUB 52
24 FOR J=1 TO NF:FOR J3=1 TO ND(J):Y1(J3,J)=Y0(J3+1,J)*H+Y0(J3,J):
. . Y(J3,J)=Y1(J3,J):NEXT J3,J:GOSUB 56
26 FOR J=1 TO NF:FOR J3=1 TO ND(J):Y1(J3,J)=(Y0(J3+1,J)+Y1(J3+1,J))*H*.5+
. . Y0(J3,J):Y2(J3,J)=Y1(J3+1,J)*H2+Y0(J3,J):Y(J3,J)=Y1(J3,J):NEXT J3,J:
. . GOSUB 56:GOSUB 58
28 FOR J=1 TO NF:IF ABS(Y2(ND(J),J))<1 THEN RA(J)=RP ELSE RA(J)=1
30 NEXT
32 FOR J=1 TO NF:FOR J3=1 TO ND(J):Y1(J3,J)=FNY1:Y2(J3,J)=FNY2:
. . Y(J3,J)=Y1(J3,J):NEXT J3,J:GOSUB 56:GOSUB 58
34 FOR J=1 TO NF:R1(J)=Y(ND(J),J)*RA(J):NEXT
36 FOR J=1 TO NF:FOR J3=ND(J) TO 1 STEP-1:Y1(J3,J)=FNY1:Y2(J3,J)=FNY2:
. . Y(J3,J)=Y1(J3,J):NEXT J3,J:GOSUB 56:GOSUB 58
38 FOR J=1 TO NF:J3=ND(J):R2(J)=Y(J3,J)*RA(J):Y2(J3,J)=FNY2:Y(J3,J)=Y2(J3,J):
. . R3(J)=Y(J3,J)*RA(J):RA(J)=RM*ABS(R3(J)):NEXT
40 GOSUB 44:IF J>NF THEN GOSUB 60:X=X2:GOSUB 54:X0=X2:GOSUB 46 ELSE
. . IF EE<&H4000 THEN EE=EE*2:ES=EB*2-1:EB=EE+1 ELSE PRINT"EE>&h4000":END
42 EB=EB+1:WEND:IF EB>EE+1 THEN WEND ELSE NEXT IB:END
44 FOR J=1 TO NF:IF ABS(R2(J)-R3(J))<RA(J) THEN NEXT:RETURN ELSE RETURN
46 GOSUB 50:IF J>NF THEN IF EE>1 AND(EB MOD 2=0)THEN EE=EE\2:ES=EB\2+1:
. . IF ES=<EE THEN EB=EE+1
48 RETURN
50 FOR J=1 TO NF:IF ABS(R1(J)-R3(J))<RA(J) THEN NEXT:RETURN ELSE RETURN
52 H2=X2-X0:H=H1*.5:H3=H/12:H4=H2/6:X1=X0+H:RETURN
54 GOSUB 62:FOR J=1 TO NF:Y0(ND(J)+1,J)=F(J):FOR J3=1 TO ND(J):
. . Y0(J3,J)=Y(J3,J):NEXT J3,J:RETURN
56 X=X1:GOSUB 62:FOR J=1 TO NF:Y1(ND(J)+1,J)=F(J):NEXT:RETURN
58 X=X2:FOR J=1 TO NF:FOR J3=1 TO ND(J):Y(J3,J)=Y2(J3,J):NEXT J3,J:GOSUB 62:
. . FOR J=1 TO NF:Y2(ND(J)+1,J)=F(J):NEXT:RETURN
60 X#=X2:GOSUB 66:FOR J=1 TO NF:YY#=Y(1,J):PRINT USING
. . " Y(#)=##.#######^^^^ True=##.########^^^^";J;YY#;Y#(J);:NEXT:PRINT:RETURN

62 F(1)=998*Y(1,1)+1998*Y(1,2):F(2)=-999*Y(1,1)-1999*Y(1,2):RETURN
64 XB=0:XE=50:N=500:NF=2:ND(1)=1:Y(1,1)=1:ND(2)=1:Y(1,2)=0:RETURN
66 Y#(1)=2*EXP(-X#)-EXP(-1000*X#):Y#(2)=EXP(-1000*X#)-EXP(-X#):RETURN
[Note] NF=the total number of differential equations, ND(k)=the order of
differential equation F(k), Y(n+1,k)=yk(n).


. . Program 4.1 has the subroutines for solving the stiff system of first order differential equations expressed in Eqs.(4.2). The condition for existence of solutions is already represented as h<0.000998, which is obtained by the second order differential equation equivalent to Eqs.(4.2). In order to obtain the accurate results around t=0, the condition is more severe as mentioned before. It is the same with the system of first order differential equations. Table 4.1 shows the results by Program 4.1. The first step is divided by 2048 and a half of the step interval comes to h=0.05/2048.

Eq4_2

Table 4.1 The solution of Eqs.(4.2) with basic interval 2h=0.1.
IBEBEEt (exp)y1Accurateexpy2Accurateexp
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20		 1
20
11
40
21
36
19
26
14
18
10
11
32
32
96
64
128
128
128
128
64
128
128
128
128
128
128
128
64
128
64
64
32
64
128		 2048
2048
1024
1024
512
512
256
256
128
128
64
64
128
64
128
64
128
128
128
128
64
128
128
128
128
128
128
128
64
128
64
64
32
64
128		 4.88281(-5)
9.76562(-4)
1.07422(-3)
3.90625(-3)
4.10156(-3)
7.03125(-3)
7.42188(-3)
0.0101563
0.0109375
0.0140625
0.015625
0.0171875
0.025
0.05
0.075
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0		 1.0475576
1.6214446
1.6562884
1.9720868
1.9752667
1.9851029
1.9846131
1.9797512
1.9782262
1.9720711
1.9689929
1.9659190
1.9506201
1.9024584
1.8554869
1.8096740
1.6374605
1.4816362
1.3406390
1.2130588
1.0976230
9.9317253
8.9865988
8.1314176
7.3576128
6.6574448
6.0239094
5.4506582
4.9319580
4.4626218
4.0379471
3.6536843
3.3059886
2.9913905
2.7067178		 1.04755755
1.62144438
1.65628823
1.97208694
1.97526688
1.98510300
1.98461317
1.97975147
1.97822642
1.97207105
1.96899271
1.96591869
1.95061982
1.90245885
1.85548697
1.80967483
1.63746150
1.48163642
1.34064008
1.21306132
1.09762325
9.93170619
8.98657918
8.13139290
7.35758882
6.65742152
6.02388395
5.45063547
4.93193940
4.46260320
4.03793026
3.65367031
3.30597753
2.99137246
2.70670566		 +00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
+00
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01		 -4.7606375
-6.2242049
-6.5736192
-9.7598553
-9.7935998
-9.9210954
-9.9200749
-9.8985618
-9.8910415
-9.8603511
-9.8449636
-9.8295945
-9.7531003
-9.5122916
-9.2774343
-9.0483701
-8.1873018
-7.4081802
-6.7031950
-6.0652941
-5.4881144
-4.9658629
-4.4932991
-4.0657088
-3.6788061
-3.3287224
-3.0119547
-2.7253291
-2.4659789
-2.2313108
-2.0189735
-1.8268421
-1.6529940
-1.4956951
-1.3533589		 -4.76063739
-6.22420463
-6.57361868
-9.75985575
-9.79360041
-9.92109585
-9.92007572
-9.89856317
-9.89104318
-9.86035133
-9.84496273
-9.82959328
-9.75309912
-9.51229424
-9.27743484
-9.04837417
-8.18730751
-7.40818212
-6.70320042
-6.06530660
-5.48811623
-4.96585310
-4.49328959
-4.06569645
-3.67879441
-3.32871076
-3.01194198
-2.72531774
-2.46596970
-2.23130160
-2.01896513
-1.82683515
-1.65298876
-1.49568623
-1.35335283		 -02
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01
-01

Return to CONTENTS