2.7 The definite integral by the numerical solution of differential equations.
. . The definite integral of a function f(t) from a to b is equivalent to the numerical solution at t=b of the differential equation shown in Eqs.(2.5). The author's variable pitch method using 3 points obtains the solution without varying the step interval 2h given previously and the solution is not always correct. The reason is that the last corrected value in the three times iterations is always equal to the first and second corrected values in any step interval because the differential equation has not the solution y in the right side.
Eq2_5
. . However, the solution y and the function f(t) are not independent of each other so the interval h, that is, a half of the step interval must sufficiently satisfy the condition for existence of solutions represented in Eq.(2.6) from Theorem 1.4 in section 1.5.
Eq2_6
. . In order to obtain the more accurate result, the differential equation must be converted into higher order differential equation with y or its derivatives in the right side. The method can stably calculate the definite integrals with ill condition given below. These are represented in Journal of IPSJ(2/'98).
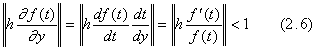
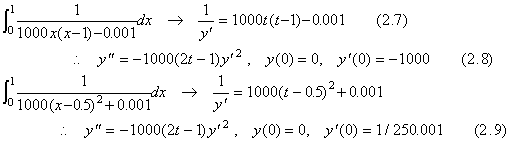
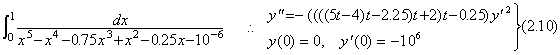
Eq2_7 Eq2_10
. . The differential equation in Eq.(2.8) has the condition for existence of solutions in Eq.(2.11) for the narrow range where it is able to assume that the function 1000(2t−1) is constant with respect to y' . It shows that the value h must be very small around t=0 and t=1 but it may be very large for the range 0.1<t<0.9. Hence Program 2.2 in section 2.3 may solve it with the very large interval such as the basic step interval of 2h=0.02. However, the value h causes an overflow of calculation around t=0 because the values of the derivatives are unusually large.
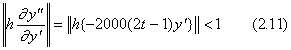
Eq2_11
. . In order to avoid the overflow, the proper value, which must be 2n and less than 8388609, must previously be substituted into the variable EE, which represents the variable subdivision of the interval 2h. The statement of the substitution is given in Line 58 of Program 2.2 and in order to obtain the effect, the statement "EE=1" must be transposed to the top of Line 16 from the top of Line 18. If the statement "EE=2n" is not given in Line 58, the statement "EE=1" in Line 16 becomes effective. Furthermore, it is necessary to cancel the declaration of integer for the variable with the character E at the head and to give the procedure detecting that the value EB is even.
. . These rewritten parts are represented in Program 2.4 by use of bold-faced type. Program 2.4 also has not the statement printing the accurate solution for comparison with the numerical solution and Line 60 has only the statement of carriage return. If the accurate solution is necessary, Line 60 must have the statement calculating it by use of X#, which has the value X2 appended zero to the tail, and printing it as follows.

60 Y#=f(X#):PRINT USING"True=##.########^^^^";Y#:RETURN

Program 2.4
10 DIM Y0(6),Y1(6),Y2(6),Y(6):DEFINT J
12 DEF FNY1=(5*Y0(J3+1)+8*Y1(J3+1)-Y2(J3+1))*H3+Y0(J3):DEF FNY2=(Y0(J3+1)+
. . 4*Y1(J3+1)+Y2(J3+1))*H4+Y0(J3):DEF FNM=INT(EB-INT(EB/16384!)*16384!)MOD 2
14 RP=16777216#:RM=2/RP
16 EE=1:GOSUB 58:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE;" N=";N;" H=";H0:N1=ND+1
18 XL=XB:X=XB:GOSUB 48:FOR IB=1 TO N:ES=1:XI=XL:XL=XB+H0*IB:X0=XI
20 WHILE 2:H1=H0/EE:EB=ES:JM=FNM:WHILE EB=<EE:X2=XI+H1*EB:IF EB=EE THEN X2=XL
22 LOCATE 0,CSRLIN:PRINT"IB=";IB;" EB=";EB;" EE=";EE;" X=";X2;:GOSUB 46
24 FOR J3=1 TO ND:Y1(J3)=Y0(J3+1)*H+Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 50
26 FOR J3=1 TO ND:Y1(J3)=(Y0(J3+1)+Y1(J3+1))*H*.5+Y0(J3):Y2(J3)=Y1(J3+1)*H2+
. . Y0(J3):Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52
28 IF ABS(Y2(ND))<1 THEN RA=RP ELSE RA=1
30 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52
32 R1=Y(ND)*RA
34 FOR J3=ND TO 1 STEP-1:Y1(J3)=FNY1:Y2(J3)=FNY2:Y(J3)=Y1(J3):NEXT:GOSUB 50:
. . GOSUB 52
36 R2=Y(ND)*RA:J3=ND:Y2(J3)=FNY2:Y(J3)=Y2(J3):R3=Y(ND)*RA:RA=RM*ABS(R3)
38 IF ABS(R2-R3)<RA THEN GOSUB 54:X=X2:GOSUB 48:X0=X2:GOSUB 42 ELSE IF EE
. . <8388608! THEN EE=EE*2:ES=EB*2-1:EB=EE+1 ELSE PRINT"EE>8388608!":END
40 EB=EB+1:JM=JM XOR 1:WEND:IF EB>EE+1 THEN WEND ELSE NEXT IB:END
42 IF ABS(R1-R3)<RA THEN IF EE>1 AND JM=0 THEN EE=EE/2:ES=EB/2+1:IF ES=<EE
. . THEN EB=EE+1 ELSE EB=EE
44 RETURN
46 H2=X2-X0:H=H1*.5:H3=H/12:H4=H2/6:X1=X0+H:RETURN
48 GOSUB 56:Y0(N1)=F:FOR J3=1 TO ND:Y0(J3)=Y(J3):NEXT:RETURN
50 X=X1:GOSUB 56:Y1(N1)=F:RETURN
52 X=X2:FOR J3=1 TO ND:Y(J3)=Y2(J3):NEXT:GOSUB 56:Y2(N1)=F:RETURN
54 YY#=Y(1):LOCATE 40,CSRLIN:PRINT USING" Y=##.#######^^^^ ";YY#;:X#=X2:
. . GOSUB 60:RETURN

56 F=-1000*(2*X-1)*Y(2)*Y(2):RETURN
58 XB=0:XE=1:N=50:ND=2:Y(1)=0:Y(2)=-1000:EE=65536!:RETURN
60 PRINT:RETURN
[Note] Y(k+1)=y(k), ND=n-th order. N=the number of equidistances between XB to XE.

. . The results of the above program and Eqs.(2.9) and Eqs.(2.10) are stably obtained as represented in Table 2.11, Table 2.12 and Table 2.13. However, these values at t=1 are significant in three or two figures. There are the two causes by which these results have the large errors and it is easily possible to remove the errors.
. . The value at t=0.5 in Table 2.11 is correct in single precision. The value at t=1 must be twice that value because the function y' (t) is symmetrical with respect to the line t=0.5. Hence the error occurs in the range from 0.5 to 1. One of the cause is that the value t is not vary around nearly one because the value h is negligible for one as shown in Table 2.11. It causes that the calculation of (h+t)−t is not associative and the equality (1−h){(1−h)−1}=h(h−1) is not satisfied in Eq.(2.7). The another cause is that the numerical solution of differential equations has slightly worse results when the differential equations are solved towards the worse condition for existence of solutions.
Table 2.12 The result of Eqs.(2.9)
58 XB=0:XE=1:N=50:ND=2:Y(1)=0:
. .Y(2)=1/250.001:RETURN
IBEBEEty
1
1
2
2
3
3
4
4
5
5
10
15
20
23
24
25
25
25
25
25
25
25
25
25
26
26
26
26
26
26
27
28
30
35
40
45
50		 1
2
1
2
1
2
1
2
1
2
2
4
8
8
7
7
71
203
467
248
497
498
250
256
1
3
19
32
34
41
4
8
8
4
4
4
2		 2
2
2
2
2
2
2
2
2
2
2
4
8
16
32
64
128
256
512
256
512
512
256
256
128
256
512
256
128
64
32
16
8
4
4
4
2		 0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.2
0.3
0.4
0.45
0.464375
0.482187
0.491094
0.495859
0.498242
0.499375
0.499414
0.499453
0.499531
0.5
0.500156
0.500234
0.500742
0.5025
0.505313
0.512812
0.5225
0.55
0.6
0.7
0.8
0.9
1		 4.0816158(-5)
8.3332983(-5)
1.2765902(-4)
1.7391227(-4)
2.2222122(-4)
2.7272600(-4)
3.2557984(-4)
3.8095051(-4)
4.3902217(-4)
4.9999746(-4)
1.3333234(-3)
2.9999593(-3)
7.9996558(-3)
1.7997207(-2)
2.6062449(-2)
5.4078560(-2)
1.0978933(-1)
2.3475608(-1)
5.1309919(-1)
9.9670964(-1)
1.0243102
1.0528332
1.1125995
1.5316864
1.6794735
1.7513239
2.1439555
2.6857326
2.8794148
2.9874856
3.0209548
3.0453715
3.0553691
3.0603690
3.0620351
3.0628688
3.0633688
Table 2.11 The result of Eqs.(2.8)
by Program 2.4
IBEBEEty
1
1
1
1
1
1
1
1
1
1
1
1
2
5
10
15
20
25
30
35
40
45
47
49
50
50
50
50
50
50
50
50
50
50
:
:
50		 1
2
3
4
5
9
17
21
23
22
22
21
5
8
2
2
1
1
1
1
2
4
7
7
37
227
993
4067
16357
65507
262119
524267
524275
524276
:
:
524288		 524288
524288
524288
524288
524288
262144
65536
16384
4096
1024
256
64
16
8
2
2
1
1
1
1
2
4
8
16
64
256
1024
4096
16384
65536
262144
524288
524288
524288
:
:
524288		 3.8147(-8)
7.62939(-8)
1.14441(-7)
1.52588(-7)
1.90735(-7)
6.86645(-7)
5.18799(-6)
2.56348(-5)
1.12305(-4)
4.29687(-4)
1.71875(-3)
0.0065625
0.02625
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0.9375
0.96875
0.991562
0.997734
0.999394
0.999858
0.999967
0.999991
0.999998
0.999999
0.999999
1
:
:
1		 -3.7437367(-5)
-7.3523603(-5)
-1.0835286(-4)
-1.4200975(-4)
-1.7457065(-4)
-5.2274170(-4)
-1.8226126(-3)
-3.2822378(-3)
-4.7301855(-3)
-6.0658026(-3)
-7.4516418(-3)
-8.7958472(-3)
-1.0202040(-2)
-1.1618270(-2)
-1.2429194(-2)
-1.2968186(-2)
-1.3410017(-2)
-1.3815480(-2)
-1.4220944(-2)
-1.4662774(-2)
-1.5201767(-2)
-1.6012691(-2)
-1.6523510(-2)
-1.7249428(-2)
-1.8581934(-2)
-1.9902581(-2)
-2.1222433(-2)
-2.2669805(-2)
-2.4100443(-2)
-2.5328130(-2)
-2.6502829(-2)
-2.6958300(-2)
-2.7122395(-2)
-2.7158681(-2)
:
:
-2.7508408(-2)

Table 2.13 The result of Eqs.(2.10)
56 F=-((((5*X-4)*X-2.25)*X+2)*X-.25)*Y(2)*Y(2):RETURN
58 XB=0:XE=1:N=50:ND=2:Y(1)=0:Y(2)=-1E+6:EE=4096:RETURN
IBEBEEtyIBEBEEty
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
10
13
15
20
23
24
25
25
25		 1
2
9
19
20
21
21
22
21
21
20
4
4
4
4
1
1
4
8
8
1
3
69
207		 131072
131072
65536
16384
4096
1024
512
256
128
64
32
16
8
4
4
1
2
4
8
16
32
64
128
256		 1.52588(-7)
3.05176(-7)
2.74658(-6)
2.31934(-5)
9.76562(-5)
4.10156(-4)
8.20312(-4)
1.71875(-3)
3.28125(-3)
0.0065625
0.0125
0.025
0.05
0.08
0.1
0.2
0.25
0.3
0.4
0.45
0.460625
0.480937
0.490781
0.496172		 -1.4974946(-1)
-2.9409441(-1)
-2.0909696(+0)
-7.6668930(+0)
-1.2942420(+1)
-1.8565838(+1)
-2.1325554(+1)
-2.4288406(+1)
-2.6895609(+1)
-2.9719023(+1)
-3.2393227(+1)
-3.5377960(+1)
-3.8604725(+1)
-4.1088379(+1)
-4.2424946(+1)
-4.8147083(+1)
-5.1261372(+1)
-5.5182976(+1)
-7.1188240(+1)
-9.9705544(+1)
-1.1463088(+2)
-1.8801512(+2)
-3.3609390(+2)
-7.0923834(+2)		 25
26
26
26
27
28
28
30
35
38
40
45
48
48
49
50
50
50
50
50
50
50
50
50		 128
11
35
38
5
7
8
8
4
2
2
1
2
8
11
39
229
995
4067
16359
65515
262133
524283
524288 		128
256
128
64
32
16
16
8
4
4
2
1
4
8
16
64
256
1024
4096
16384
65536
262144
524288
524288 		0.5
0.500859
0.505469
0.511875
0.523125
0.54875
0.55
0.6
0.7
0.75
0.8
0.9
0.95
0.96
0.97375
0.992187
0.997891
0.999434
0.999858
0.999969
0.999994
0.999999
1
1		 -2.6021067(+3)
-3.3845398(+3)
-4.6770024(+3)
-4.9263677(+3)
-5.0333604(+3)
-5.0927793(+3)
-5.0941147(+3)
-5.1201094(+3)
-5.1333867(+3)
-5.1362910(+3)
-5.1384429(+3)
-5.1419985(+3)
-5.1441265(+3)
-5.1447036(+3)
-5.1457168(+3)
-5.1483579(+3)
-5.1510396(+3)
-5.1536812(+3)
-5.1564380(+3)
-5.1594126(+3)
-5.1621450(+3)
-5.1643613(+3)
-5.1649092(+3)
-5.1651519(+3)
. . In order to avoid the errors, the integral range must be separated into the two ranges of [0, 0.5] and [0.5, 1], and the second range must be shifted to left by one, that is, y' (t) must be substituted u=t−1 and rearranged with the variable u. Furthermore, the integral between the limits must be carried out from 0 to −0.5 as shown in Eq.(2.12). It is obtained by Program 2.4 given below subroutines and the result comes to the same value as the integral between zero to 0.5 except the sign is changed.
Eq2_12
=−1.3815480×10−2−1.3815480×10−2=−2.7630960×10−2
where the differential equation of the second term comes to,
Eq2_13
56 F=-1000*(2*X+1)*Y(2)*Y(2):RETURN
58 XB=0:XE=-0.5:N=25:ND=2:Y(1)=0:Y(2)=-1000:EE=65536!:RETURN
. . Table 2.12 shows that the differential equation in Eqs.(2.9) has the worse condition for existence of solutions around nearly t=0.5 so the integrand in Eqs.(2.9) must be shifted to left by 0.5 and integrated as follows.
Eq2_14
=1.5687959−(−1.5687959)=3.1375918
where the differential equation comes to,
Eq2_15
In this case, the value EE may be given 256 for the basic division N=25.
. . Table 2.13 shows that the differential equation in Eqs.(2.10) has the worse condition for existence of solutions around nearly t=0, t=0.5 and t=1 so the integral range must be separated four ranges of [0, 0.25][0.25, 0.5][0.5, 0.75] and [0.75, 1]. The second and third ranges must be shifted to left by 0.5 and the fourth range must be shifted to left by one. The integral of these ranges must be carried out as follows.
Eq2_16
=−51.261383−2565.9854+(−2549.3049)−28.693586=−5195.2452
where the differential equations for 0.25≤t≤1 come to,
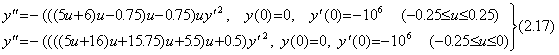
Eq2_17
. . These results of definite integrals in the three examples are all significant in single precision and need about two to four minutes with the computer using 8086 CPU at 10 MHz clock cycle.

Return to CONTENTS