The new method for the numerical solution (c) 1997 Akio Wakabayashi

1. The new method for the numerical solution of ordinary differential equations.

1.1 Summary explanation of the operational calculus.
. . When f₀, f₁, f₂, f₃, ........ are the values of f(t) for equidistant variables t_k=t₀+kh, k=0,1,2,3,......., the function f(t) is expressed by Newton's interpolation formula and the integrals y_k for equidistant variables t_k are expressed by Stirling's integral formula. Therefore the finite differences of y_k are expressed by the formulas with the finite differences of f_k. The expressions may be written in the form of the matrix equation such as Eq.(1.1).
. . The matrix is upper triangular matrix whose i-th row has the same elements as the (i−1)th row except that they are shifted to the right by one column and the first column is zero, where the first row is the following.

. . The author uses D⁻¹ for the matrix because of the inverse matrix of the differential matrix D and names it integral matrix and names hD⁻¹ integral operator. Then the m multiple integral of f(t) is expressed in

, where Δ^mY and F are the vectors expressed in,

The elements of these vectors are the successive differences of the analytical functions approximated by Newton's interpolation formula. It is the same to use backward formula.
. . The matrix of Eq.(1.1) has the third row [0 0 1] and the vector of the left side has Δ³y₀=hΔ²f ₀. But it is negligible when the integral over the range [t₀, t₂] is accurate enough because that Newton's interpolation formula has y₀, Δy₀, Δ²y₀ and the remainder over the range. Therefore the integral may be written in the form of Eq.(1.1). It is similar when the equidistant points are more than 3 points.

1.2 The numerical solution of ordinary differential equations.
. . When y' =f(y, t) and y₀ are given, Δy₀ is predicted by using the sub-matrix of 1 row and 1 column in Eq.(1.1). Then Δy₀ is corrected and Δ²y₀ is predicted by using the sub-matrix of 2 rows and 2 columns and using Δf₀ which is obtained by f(y, t). Last, Δy₀ and Δ²y₀ are corrected several times by using the sub-matrix of 2 rows and 3 columns and using Δf₀ and Δ²f₀ which is corrected by f(y, t). Then starting point is shifted to t₂ and the same procedure is repeated.

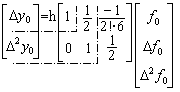(1.1)
. . When the n+1 points are equidistant, the integral of the range [t₀, t_n] is obtained in a similar way and the starting point is shifted to t_n. The new range may have any number of equidistant points by any interval, if the integral is convergent. The reason is that the method is able to start from only the initial value and that all the other values are predicted and corrected.
. . When the total range is divided into n of equidistances and the sub-range is divided into 2 of equidistances, the total solutions may be obtained by n steps of Eq.(1.1). It introduces the simple and new method as follows, which gives better results than Runge-Kutta's method. Hereafter, the variable t has a real number and the variable x has the value rounded in some accuracy.

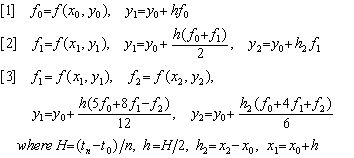(1.2)
. . The procedure [1] predicts y₁ by Euler's rule. The procedure [2] corrects y₁ by the trapezoidal rule and predicts y₂ by the midpoint rule using the same f₁. The procedure [3] corrects y₁ by Adams-Moulton's rule of degree 3, which has negative equidistances and corrects y₂ by Simpson's rule using the same f₁ and f₂.
. . The procedure [3] is repeated two times more. The reason is that the f₁ and f₂ have not used the y₁ and y₂ of the procedure [3] so these and then the y₁ and y₂ should be corrected and these should be convergent by once more procedure [3]. If it is not convergent, the interval h is not proper. It is mentioned afterwards why the interval is not H but h₂=x₂−x₀.
. . There are two methods to solve the n-th ordinary differential equation accelerated by z(t). The one is slightly complex because it has to calculate the polynomial of the matrix D and the reverse matrix of the polynomial. The other is simple because of repeating n times the method of Eqs.(1.2) whereas the differential equation is expressed in Eqs.(1.3).

(1.3)

. . At first, the procedure [1] is repeated n times to predict the values of y⁽ⁿ⁻¹⁾ to y for x₁. Then the procedure [2] is repeated n times to correct the values for x₁ and to predict the values for x₂. And then the procedure [3] is repeated n times to correct the values for x₁ and x₂.
. . The procedure [3] is repeated twice more for the first equation of Eqs.(1.3) but once more for the others. Because it may be considered that the first equation is the first-order differential equation of y⁽ⁿ⁻¹⁾ with the others which are the parts to calculate the function f of the right side.
. . The usual method replaces the first equation of Eqs.(1.3) by a system of n first-order equations by use of a simple substitution technique. It is expressed in the variables y₁ to y_n substituted respectively for the variables y to y⁽ⁿ⁻¹⁾ of Eqs.(1.3). The method of the solution successively integrates the first-order equations and comes to the same as the author's method except that the author's method dose not need any substitution technique and needs to be given only the first equation of Eqs.(1.3) because that the other equations are in use with any differential equation.

1.3 Program and results.
. . The author's method may be written in BASIC as in Program 1. It is able to solve first order to 5-th order differential equations because of dimensional size being six. The program has to be given the sub-routines in the line 56 and 58, where the one gives the right side of the first equation of Eqs.(1.3) and the other gives the total range, the number of equidistaces, the order of differential equation and initial values. The line 60 gives the values of the true solutions for comparison to the results but may be not given together with the code "X#=X2:GOSUB 60" and the variable Y# in the line 54.
. . The values of solutions are decimalized to the floating number of eight figures after being converted to the double length in binary with zero of single length in the tail.

Program 1

10 DIM Y0(6),Y1(6),Y2(6),Y(6):DEFINT E,J
12 DEF FNY1=(5*Y0(J3+1)+8*Y1(J3+1)-Y2(J3+1))*H3+
. . Y0(J3):DEF FNY2=(Y0(J3+1)+4*Y1(J3+1)+Y2(J3+1))
. . *H4+Y0(J3)
16 GOSUB 58:H0=(XE-XB)/N:PRINT"X= ";XB;"-";XE;
. . " N=";N;" H=";H0:N1=ND+1
18 X2=XB:FOR IB=1 TO N:X0=X2:X2=XB+H0*IB:X=X0:
. . GOSUB 48
22 LOCATE 0,CSRLIN:PRINT"IB=";IB;" X=";X2;:
. . GOSUB 46
24 FOR J3=1 TO ND:Y1(J3)=Y0(J3+1)*H+Y0(J3):
. . Y(J3)=Y1(J3):NEXT:GOSUB 50
26 FOR J3=1 TO ND:Y1(J3)=(Y0(J3+1)+Y1(J3+1))*H*
. . .5+Y0(J3):Y2(J3)=Y1(J3+1)*H2+Y0(J3):
. . Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52
30 FOR J3=1 TO ND:Y1(J3)=FNY1:Y2(J3)=FNY2:
. . Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52
34 FOR J3=ND TO 1 STEP-1:Y1(J3)=FNY1:Y2(J3)=FNY2
. . :Y(J3)=Y1(J3):NEXT:GOSUB 50:GOSUB 52
36 J3=ND:Y2(J3)=FNY2:Y(J3)=Y2(J3)
40 GOSUB 54:NEXT IB:END
46 H2=X2-X0:H=H0*.5:H3=H/12:H4=H2/6:X1=X0+H:
. . RETURN
48 GOSUB 56:Y0(N1)=F:FOR J3=1 TO ND:Y0(J3)=Y(J3)
. . :NEXT:RETURN
50 X=X1:GOSUB 56:Y1(N1)=F:RETURN
52 X=X2:FOR J3=1 TO ND:Y(J3)=Y2(J3):NEXT:
. . GOSUB 56:Y2(N1)=F:RETURN
54 X#=X2:GOSUB 60:YY#=Y(1):LOCATE 40,CSRLIN:PRINT
. . USING"Y=##.#######^^^^ True=##.######## ^^^^";
. . YY#;Y#:RETURN
56 F=-2*Y(1)-2*Y(2):RETURN
58 XB=0:XE=90:N=900:ND=2:Y(1)=0:Y(2)=1:RETURN
60 Y#=EXP(-X#)*SIN(X#):RETURN
[Note] Y(k+1)=y^(k), ND=n-th order.
. . N=the number of equidistances between XB to XE.

. .

(1.4)
. . Program 1 has the sub-routines to solve Eq.(1.4) with the equidistances of 2h=0.1 and Table 1 represents a part of the solutions together with the Runge-Kutta's ones. The author's results are better about one figure than Runge-Kutta's ones as in the table. There are several reasons mentioned below.

Table 1. The solutions of Eq.(1.4).
t	Author	Runge-K	True value	Exp
0.1 0.2 0.3 0.4 2.0 3.0 4.0 10.0 20.0 30.0 40.0 83.0 84.0 85.0	9.0333059 1.6265677 2.1892685 2.6103503 1.2305982 7.0258616 −1.3861313 −2.4698591 1.8817083 −9.2454568 3.1653754 8.7012940 2.4258100 −2.1319470	9.0333343 1.6265723 2.1892738 2.6103556 1.2305877 7.0253122 −1.3861323 −2.4699193 1.8816610 −9.2445311 3.1646361 8.6687695 2.4146370 −2.1310768	9.03330122 1.62656693 2.18926760 2.61034923 1.23060025 7.02595149 −1.38613212 −2.46985202 1.88172041 −9.24562742 3.16550467 8.70155450 2.42370770 −2.14125438	−02 −01 −01 −01 −01 −03 −02 −05 −09 −14 −18 −37 −37 −38

1.4 The Accuracy of solutions.
. . When a half of the integral interval is expressed by the sign h, the solution of Eq.(1.4) is expanded in a series by the procedure [1][2][3] and [3]. It comes to Eq.(1.5) for x=2h. Runge-Kutta's solution is also expanded in the series without the last term, the denominator of which is 30 in Taylor's expansion. Table 1 represents the relation between the three.

(1.5)
. . When the procedure [3] is not repeated, the last term does not appear. When the procedure [3] is repeated more than twice, the terms of higher than 6th power of 2h appear but these are not correct. If these are not negligible, the numerical solution converges to the slightly different value from the true solution as in usual P-C method and the interval h is not proper. These are the reason of the three times the procedure [3] for the solution y' of y"=f(y' ) in Eq. (1.4).
. . Runge-Kutta's method may be written as follows by using x₁, f₁, y₁ and h for the midpoint and using x₂, f₂, y₂ and 2h for the end point of the interval. It is different from the author's method that the procedure [2'] corrects y₁ by Euler's backward rule and then corrects f₁ and the procedure [3'] corrects y₂ by Simpson's rule using the average value of the two f₁ and does not correct y₁. It is not certain that the repeat of the procedure [3'] is valid or not.

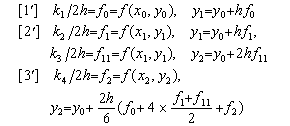(1.6)
. . For example, the solution of dy/dt =−y, y(0)=1 is expanded in the Taylor's expansion of 4th degree and once more the procedure [3'] obtains no difference because k₄ is determined by y₀+k₃ depending on only the value of function f for midpoint. However, if y₂ of the procedure [3'] is replaced on y₀+k₃ because it is the predicted value for x=2h as in Eqs.(1.6), the repeat obtains the term of 5th power of 2h being not correct and changes the term of 4th power for incorrect one. And the numerical result changes for the worse as in Table 2 which represents the case of 2h=0.2.

Table 2. The results repeated [3] and [3']
Author's method Runge-Kutta True
1×[3]
2×[3]
3×[3] 0.8186667
0.8187333
0.8187311 1×[3']
2×[3']
3×[3'] 0.8187333
0.8187089
0.8187097

0.81873075
. . The author's method also represents that the term of h⁴ is not always equal to the term of Taylor's expansion. The author's method does not obtain Taylor's expansion but obtains the integral of Newton's interpolation formula. The one is not better approximation than the other in case of large h.When the three points are equidistant, the function f(t) is expressed in Taylor's expansion of 2nd degree with the remainder and the integral is expressed in Taylor's expansion of 3rd degree with the integral of the remainder which consists of the terms of h⁴ and higher power of h. The author's remainder has the slightly different term of 4th power from Taylor's expansion but the total remainder is better approximation than Runge-Kutta's one. Therefore the author's results are better as in Table 1, Table 2 and Table 3.
. . When the solution should be approximated by Taylor's expansion of higher than 4th degree, for example, in the case of dy/dt=y⁻¹, y(0)=0.5, 2h=0.125, the author's result is better by about 3 figures than Taylor's expansion of 7th degree as in Table 3. The integral of y⁻¹ by Simpson's 1/3 rule is also better by about 2 figures than Taylor's expansion. That is, it is not important that the term of 4th power is equal to the one of Taylor's expansion. It is important accurately to approximate the total of higher terms than 3rd power. So the method should be introduced by Stirling's integral formula.

Table 3. dy/dt=y⁻¹, y(0)=0.5, 2h=0.125
t Author's Simpson Runge-K Taylor(7) True
0.125 0.7071319 0.7072122 0.7071896 0.7106933 0.70710678
. . Runge-Kutta's result is better by about 2 figures than Taylor's expansion of 7th degree, though the method is so introduced that the terms up to 4th power is equal to the ones of Taylor's expansion and that the higher terms than 4th power should be negligible. The reason is that the procedures are similar to the author's method as in Eqs.(1.6). But it is not able to give proof of the fact by the author's operational calculus.

1.5 The condition for existence of solutions.
. . The values of y₁ and y₂ obtained by the procedures [1][2][3][3][3] in Eqs.(1.2) should respectively be the progression which converges to the solution of the differential equation. It is the same with y⁽ⁿ⁻¹⁾ of the first equation of Eqs.(1.3), because it may be considered as the first-order differential equation of y⁽ⁿ⁻¹⁾. Therefore the right side of it must satisfy Lipschitz's condition but it is not sufficient.

. . [Theorem 1.1]. . The norm of the integral operator is equal to the interval h.
[Proof]. .There will be some point t_a such that t₀<t_a<t for which the integral of f(t) is f(t_a)(t−t₀). Then there will be some number M such that Eq.(1.7) is satisfied.

There will be a function such that the equality of Eq.(1.8) is satisfied, for example, |f(t_a)|=|f(t)|_max in the interval. In the case, the right side of Eq.(1.8) is the maximum of the left side so the infimum of M is h.

[ Q.E.D.]

. . When the function f(t) is the derivative of y(t), the integral mentioned above is the definite integral, that is, y(t₀+h)−y(t₀) or y(t₀+h) in case of y(t₀)=0. When f(t) is the n-th derivative of y(t) which has y^(k)(t₀)=0 for k=0 to n−1, the norm of the operator which plays the n multiple integral of f(t) between the interval h is introduced as follows.

. . [Theorem 1.2]. . The norm of the n multiple integral operator is equal to hⁿ/n!.
[Proof]. . The n multiple integral of f(t) is expressed in Eq.(1.9) with all the initial values being zero and with f(t) replaced on y⁽ⁿ⁾(t).

. .(1.9)

There will be some point a_k such that t₀<a_k<x_n−k, k=1 to n, (x₀=t). Because of x_n−k−t₀>0 and a_k being a function of x_n−k,
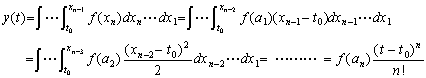
Eq15_9a

. .by such way as Eq.(1.7) and (1.8).........[ Q.E.D.]

. . The definition of differentiation is expressed in the first equation below and the integration of the derivative is expressed in the second equation because the integral operation should have the inverse operation of h→0. Therefore the norm of the integral operator is the interval h.

Usually, the second differentiation is defined in the equation below. However, the definition is not proper for comparison of the norms of the integral operator and the double integral operator, because it increases the operated interval to 2h.
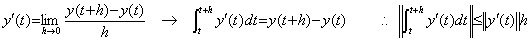
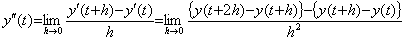
Eq15_9e

The second differentiation and the inverse operation must be defined between the interval h as follows.
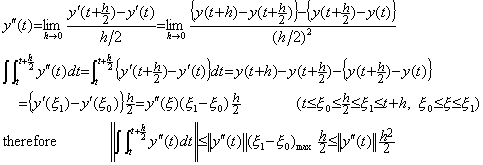
Eq15_9f

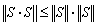Accordingly, usual inequality Eq15_9c

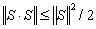as to the norm of integral operator S is very rough estimation. It should be Eq15_9g

. . [Theorem 1.3]. . The norm of the n multiple integral operator is equal to hⁿ in the calculus of finite differences.
[Proof]. . All the initial derivatives must be eliminated to obtain Newton's interpolation formula of the n multiple integral of f(t) replaced on y⁽ⁿ⁾(t) of Eq.(1.9). They are eliminated by the n-th difference of Eq.(1.9) because it is equivalent to Taylor's expansion of degree n−1 with remainder term. Hence the n-th difference of Eq.(1.9) comes to the difference of the remainder term and is obtained below.

Hence,

(1.10) There will be some point a_k such that x_k<a_k<x_k+h, k=1 to n−1, t<a_n<t+h,

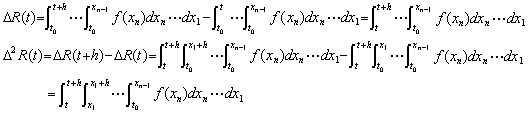
		. .(1.11)
∴. .	∴. . M_inf=hⁿ	[ Q.E.D.]

. . In the calculus of finite differences, the n multiple integral obtains the differences Δ^my(t₀) of higher degree than n−1 by Eq.(1.10), so the differences of lower degree than n must be given to obtain y(t) in stead of the initial derivatives. Eq.(1.10) also shows that any integral increases the range by h.
. . When the integrand is f(t)=t³, four equidistant points are required to express it in finite differences and the integral of f(t) requires one more point, while the norm of integral is h over the range 4h. Hence the norm between 0 to 4h is h×(4h)³=(4h)⁴/4. If the range is 0 to 3h, the norm is (3h/4)×(3h)³=(3h)⁴/4. Therefore, the calculus of the norm is of the same way as the calculus of functions together with the operation to the integrand except positive result.
. . The author's operational calculus shows them explicitly in the expression of the matrix equation. For example, the vector F in Eq.(1.1) requires the range 2h and the negligible differences of higher degree than two, and because the vector ΔY has Δ³y₀ in the expression which does not omit the 3rd row of matrix D, the vector ΔY requires the range 3h and the norm of integral is h over the range, where the norm of matrix D is one.

. . [Theorem 1.4]. . The solution of Eqs.(1.3) converges, if Eq.(1.12) is satisfied.

(1.12)
[Proof]. . When the differential equation is y' =f(y,t), y(t₀)=y₀, the solution is

(1.13) Now we may obtain an approximation y₁(t) assuming that y(t)=y₀ is an initial approximation, then we may obtain y₂(t) assuming that y=y₁(t). Thereby, we may form a sequence of functions y_i(t), i=1,2, ……. Because of theorem 1.1,
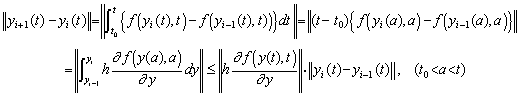Eq15_14

(1.14) Therefore if Eq15_14a

is satisfied, the sequence of functions converges to y(t).
. . When y⁽ⁿ⁻¹⁾ is replaced on y of Eq.(1.13), the parameter y^(k) is the n−1−k multiple integral of y⁽ⁿ⁻¹⁾ and by Eq.(1.10),

[ Q.E.D.]
. . The value t in the condition Eq.(1.12) must not be starting point t₀ because of Eq.(1.14) and y_i(t₀)=y(t₀), which are fixed. It should be t₀+h because of the construction of the sequence of functions y_i(t) and that finite differences do not use the maximum between t₀ to t₀+h, even if it exists.
. . This condition must be satisfied in any method of numerical solution. For example, Euler's rule obtains y₂(t) assuming that y(t)=y₀ is an initial approximation, so the true solution y₁(t) and they are expressed in Eq.(1.14) and the condition must be satisfied for y₂(t) to be better approximation.
. . The norm of integral operator is equal to the smallest interval being in use, so the norm of Runge-Kutta's method is equivalent to a half of the pitch length and the usual comparison of results with P-C methods is unfair.
. . The interval h=0.05 in the program for Eq.(1.4) sufficiently satisfies the condition of Eq.(1.12) which is h(2+2h)<1, that is, h<0.366. When the differential equation is in Eq.(1.15), the condition is h(20−2h)<1, that is, h<0.05.

y" −20y' +2y=0,

y(0)=0,

y' (0)=1,

(1.15)

. . In truth, the solutions have the accuracy of single precision for h=0.01, five significant figures for h=0.02, one significant figure for h=0.04 and do not converge for h=0.05 in case of P-C method with repeats up to convergence. The author's method has the accuracy of two significant figures for h=0.05 because of three times repeats of the procedure [3] but loses them in few steps.

1.6 Stiff differential equations and usual troubles.
. . Eq.(1.16) is called a stiff differential equation. It has the condition 100h<1 and the author's method obtains a very rough solution for h=0.01 as yet but does not obtain any approximation for h=0.015.

y' =100(sin t −y),

y(0)=0

(1.16)

. . Table 4 shows the results of Eq.(1.16) by Program 1 with following subroutines and by Runge-K's method. The both methods have the step interval of 2h=0.01, a half of which satisfies the above condition.

56 F=100*(SIN(X)-Y(1)):RETURN
58 XB=0:XE=50:N=5000:ND=1:Y(1)=0:RETURN
60 Y#=(SIN(X#)-.01#*(COS(X#)-EXP(-100*X#)))/1.0001#:RETURN

Table 4. Solutions of Eq.(1.16), h=0.005
t	author's	Runge-K	True	exp
0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 : :0.95 0.96 0.97 0.98 0.99 1.00 1.01 1.02 1.03 : :	3.6805207 1.1354182 2.0496540 3.0177828 4.0055208 5.0001867 5.9970498 6.9943063 7.9912283 8.9874871 9.9828951 1.0977323 1.1970660 1.2962803 1.3953649 : :8.0751806 8.1337517 8.1915098 8.2484484 8.3045620 8.3598453 8.4142929 8.4678990 8.5206574 : :	3.7499631 1.1405773 2.0525275 3.0192034 4.0061768 5.0004739 5.9971679 6.9943488 7.9912379 8.9874804 9.9828817 1.0977305 1.1970639 1.2962779 1.3953625 : :8.0751652 8.1337363 8.1914937 8.2484323 8.3045459 8.3598292 8.4142762 8.4678823 8.5206413 : :	3.67875972 1.13528838 2.04958203 3.01774709 4.00550414 5.00017871 5.99704594 6.99430354 7.99122609 8.98748430 9.98289234 1.09773202 1.19706571 1.29628001 1.39536462 : :8.07517915 8.13375018 8.19150785 8.24844638 8.30456007 8.35984363 8.41429089 8.46789673 8.52065579 : :	-03 -02 -02 -02 -02 -02 -02 -02 -02 -02 -02 -01 -01 -01 -01 : :-01 -01 -01 -01 -01 -01 -01 -01 -01 : :

. . The author's results are better about two figures than Runge-K's results. The both results have the worst approximation at t=0.01 and they come to the best approximation being possible by the calculus of single precision around t=0.1. It is necessary to divide the interval h more by about 50 if the first result should be obtained with single precision. The reason is that dt/dy is not negligible around t=0 and the condition for existence of solutions comes to Eq.(1.17). By the same reason, the results around t=nπ become worse.
. .

(1.17)
. . It is possible to replace the n-th order differential equation by a system of n first-order differential equations and the replacement is reversible. The system of Eqs.(1.18) are called stiff differential equations and may be rewritten in Eq.(1.19). So it has the condition h(1001+1000h)<1, that is, h<0.000998 and the author's method obtains a very rough solution for h=0.001 as yet but does not obtain any approximation for h=0.0015.

(1.18)

(1.19)
. . Eqs.(1.18) may be represented in matrix equation Y' =AY, where Y' =(y₁', y₂' ) and Y=(y₁, y₂). So the condition of convergence may be represented in the norm of matrix A, that is,

. The norm of matrix A is about |a₁₁+a₂₂|, if it is very larger than h|a₁₁a₂₂−a₁₂a₂₁|. The reason is that the matrix equation may be expressed in the 2nd differential equation as follows.
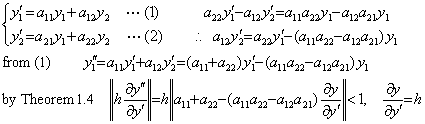
Eq15_19b

. . Table 5 shows the results of Eq.(1.19) by Program 1 with following subroutines and the results of Eqs.(1.18) by Runge-K's method. The both methods have the step interval of 2h=0.001, a half of which satisfies the above condition.

56 F=-1001*Y(2)-1000*Y(1):RETURN
58 XB=0:XE=5:N=5000:ND=2:Y(2)=998:Y(1)=1:RETURN
60 Y#=2*EXP(-X#)-EXP(-1000*X#):RETURN

:' For y₂
:' Y(2)=-999:Y(1)=0
:' Y#=-EXP(-X#)+EXP(-1000*X#)

. . The author's results are better about two figures than Runge-K's results. The both results have the worst approximation at t=0.001 and they come to the best approximation being possible by the calculus of single precision around t=0.01. It is necessary to divide the interval h more by about 20 if the first result should be obtained with single precision. The reason is that dt/dy is not negligible around t=0. However the strict condition is not obtained because Eq.(1.19) does not express the relation of y and t explicitly.

Table 5. Solutions of Eq.(1.18) and Eq.(1.19), h=0.0005
t	A's y₁	R-K	True		A's y₂	R-K	True
.001 .002 .003 .004 .005 .006 .007 .008 .009 .010 .011 .012 .013 .014 .015 : :.096 .097 .098 .099 .100 .101 .102 .103 : :	1.6299455 1.8605392 1.9441504 1.9736652 1.9832709 1.9855500 1.9851339 1.9837270 1.9819567 1.9800539 1.9781036 1.9761372 1.9741659 1.9721942 1.9702235 : :1.8169280 1.8151120 1.8132977 1.8114854 1.8096749 1.8078661 1.8060591 1.8042539 : :	1.6230011 1.8553791 1.9412748 1.9722407 1.9826094 1.9852552 1.9850063 1.9836731 1.9819344 1.9800450 1.9781002 1.9761360 1.9741657 1.9721942 1.9702235 : :1.8169277 1.8151116 1.8132974 1.8114851 1.8096745 1.8078657 1.8060588 1.8042536 : :	1.63012158 1.86066873 1.94422194 1.97370034 1.98328701 1.98555718 1.98513700 1.98372837 1.98195735 1.98005427 1.97810385 1.97613728 1.97416601 1.97219426 1.97022357 : :1.81692802 1.81511201 1.81329780 1.81148540 1.80967483 1.80786606 1.80605909 1.80425393: :		-.63094497 -.86253715 -.94714594 -.97765726 -.98825842 -.99153209 -.99210948 -.99169517 -.99091643 -.99000418 -.98904347 -.98806554 -.98708189 -.98609674 -.98511165 : : -.90846407 -.90755606 -.90664893 -.90574276 -.90483749 -.90393311 -.90302962 -.90212703 : :	-.62400055 -.85737705 -.94427019 -.97623265 -.98759675 -.99123716 -.99198174 -.99164099 -.99089390 -.98999500 -.98903978 -.98806411 -.98708141 -.98609662 -.98511159 : : -.90846390 -.90755582 -.90664870 -.90574247 -.90483725 -.90393287 -.90302938 -.90212679 : :	-.631121076 -.862666728 -.947217440 -.977692354 -.988274534 -.991539213 -.992112561 -.991696452 -.990916968 -.990004433 -.989043576 -.988065568 -.987081874 -.986096712 -.985111633 : :-.908464009 -.907556004 -.906648899 -.905742702 -.904837417 -.903933030 -.903029547 -.902126967 : :

. . It is mentioned that the differential equation Eq.(1.20) does not satisfy Lipschitz's condition at y=0, whereas it is fixed. It is not the reason of trivial solution y(t)=0. The reason is that if y(0)=0, the derivative is f(0)=0 and the results are y(h)=0, f(h)=0, y(2h)=0, f(2h)=0, and so on. The condition of convergence is Eq.(1.21) and the solution is t²/4, so if the value of starting point t₀ is very large than h, the solution converges easily but when t₀ is zero, any interval h will critically satisfy the condition in Eq.(1.21). Therefore the author's method and trapezoidal method are able to obtain the solution assuming that the initial approximation is any positive number for any point t=h without use of Euler's rule, if they are iterated up to convergence.

(1.20)
(1.21)

. . For example, the author's method obtains the solution 25 for t=10 by 23 times iterations of procedure [3] with h=5 assuming that initial approximation is two for midpoint t=5. Trapezoidal method obtains following progression for any approximation a at any h.
Eq15_20a

. . The analytical solution is obtained assuming that y is not zero and that the result may be true at t=0. Then it is seen that the combinations of the results with trivial solution y(t)=0 also satisfy the differential equation. It is the same with the numerical solution.
. . It is also mentioned that the differential equation Eq.(1.22) does not satisfy Lipschitz's condition at y=0, whereas it is fixed. The condition of convergence is Eq.(1.23) and the solution is (2t)^1/2, so if the value of starting point t₀ is very large than h, the solution converges easily but when t₀ is zero, any method can't obtain the solution with use of the derivative at t₀ because it is infinite. It may be considered to exchange the independent variable t for y and it must use the same way as Eq.(1.20).

(1.22)
(1.23)

. . It may be also considered to obtain the average derivative by use of the reciprocals of f₀ and f₁ which is a rough approximation for t=h without use of Euler's rule. The average derivative comes to two times f₁ and the iteration obtains bistable progression y₁, 2h/y₁, y₁,……, that is, the solution is infinitive because of no use of f₀, whereas it is not zero. However if the new approximation is determined by the average of two bistable values, the iteration obtains an approximation of the solution.
. . More easy method is to solve the equation y=2h/y. It gives the accurate solution for t=h but the next step loses the most of accuracy. For example, when h=0.1 and y(h)=0.447213 are given, the solution y(2h) by trapezoidal method is 0.637454, whereas the accurate value is 0.6324555. The author's method obtains 0.632478 and it is not corrected by more repeats of the procedure [3] because of incorrect terms of higher power of h. More accurate solution requires less interval than t₀=0.1 or the operational calculus of higher order.

1.7 Stability of solutions.
. . Instability of solutions depends on several causes. It is one of the causes that the condition for existence of solutions is not sufficiently satisfied. The condition of Eq.(1.24) is Eq.(1.25) so the interval h must be small according as the starting point t₀ is far from zero. If t₀ is nearly zero, the condition is h<t from Eq.(1.26). Although it is critical condition and y' (0)=0, the solution is obtained easily and accurately because y(0) is not zero then y(h) and y' (h) are not zero. For example, if h is 0.1, the integral of one step loses considerable accuracy according to approach to t=10 so any approximation is not obtain there in case of the total range from zero to ten.

. . There is the cause which the author calls the impulsive response of a differential equation by the error of initial value, because it corresponds to the solution of the differential equation driven by εδ(t). It may be mentioned as a rule that any numerical method can't obtain accurate results up to point far from zero, when the solution decreases more rapidly or increases more slowly than the impulsive response of the differential equation.

(1.27)

(1.28) . . The differential equation of Eqs.(1.27) is equivalent to that of Eqs.(1.28), that is, the initial value is equivalent to impulse function driving the differential equation with initial value of zero. So the solutions for y(0)=1 and its error are both impulsive response and the relative error of the results is constant anywhere. Hence, if Ah<1 is sufficiently satisfied, the numerical solution is stable.
. . Differentiating the differential equation of Eqs.(1.27) obtains the 2nd order differential equation of Eqs.(1.29) which has the same solution as Eqs.(1.27) but the response by the errors of initial values are very different.

(1.29) . . When y' is replaced on y in Eqs.(1.28), the solution y' is the impulsive response. The solution y, which is the integral of y' , is the impulsive response of the 2nd order differential equation if it has the initial value y(0)=0. That is, the solution of the differential equation in Eqs.(1.29) is the impulsive response if y(0)=0 and the impulse function is equivalent to the initial value y' (0) of the homogeneous differential equation. When the impulse kδ(t) drives an n-th order differential equation whose initial values are all zero, it is the impulsive response and the impulse is equivalent to the initial value y⁽ⁿ⁻¹⁾(0)=k of the homogeneous differential equation. These details are treated in the section 3.
. . The 2nd term of the solution in Eqs.(1.29) is the impulsive response by the error −Aε₁ of the initial derivative and approaches ε₁. If A is integer, the two errors ε₀, ε₁ are nearly equal and the solution is stably obtained by use of the condition Ah<1, whereas it is not impulsive response and decreases more rapidly than the impulsive response. However, if A is not integer, for example, A=1.3, the solution does not approach zero because the binary A is a recurring number and the error ε₁ is different from ε₀. If the initial values are y(0)=0 and y' (0)=−A, the solution is stable because it is the impulsive response expressed in e^−At−1.
. . The differential equation in Eqs.(1.27) is stably solved in both case of A=1 and A=2 but the differential equation which has the two solutions as the fundamental solutions is not always solved correctly. The solution in Eqs.(1.30) is impulsive response and solved correctly but the solution in Eqs.(1.31) is not solved correctly after the range where it will decrease to the impulsive response by the errors of the initial values.

y" +3y' +2y=0,

y(0)=0, y' (0)=1
y(0)=1, y' (0)=−2

then y=e^−t−e^−2t
then y=e^−2t

. .(1.30)
. .(1.31)

. . When the differential equation is y"−3y' +2y=0, the impulsive response increases rapidly than the fundamental solution e^t. So the results of the initial values y(0)=1, y' (0)=1 with the interval 2h=0.1 has no accurate place of decimals after about t=15, whereas they are very accurate around t=0.
. . Differentiating the differential equation in Eq.(1.24) obtains Eqs.(1.32). The solution is the same as that of Eq.(1.24) but the numerical solutions lose the accuracy as rapidly as Milne's results of Eq.(1.24) and after about t=5, the solution decreases stably but very slowly as in Table 6.

y" +ty' +y=0,. . y(0)=10, y' (0)=0,. . h(t+h)<1. . (1.32)

(1.33)

Table 7. The solution of y" +ty' +y=δ(t)
IB	t	y(exp)	True(exp)
1 2 3 4 5 6 7 8 9 10 20 30 40 50 60 70 80 90 100 110 120	0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0 11.0 12.0	9.9667229(-02) 1.9735435(-01) 2.9115966(-01) 3.7933365(-01) 4.6034390(-01) 5.3292733(-01) 5.9612751(-01) 6.4931524(-01) 6.9219214(-01) 7.2477829(-01) 6.3998836(-01) 3.9316690(-01) 2.7039629(-01) 2.0924576(-01) 1.7175008(-01) 1.4597256(-01) 1.2705277(-01) 1.1253712(-01) 1.0103162(-01) 9.1679864(-02) 8.3924539(-02)	9.96673339(-02) 1.97354548(-01) 2.91159949(-01) 3.79334008(-01) 4.60344283(-01) 5.32927735(-01) 5.96127869(-01) 6.49315541(-01) 6.92192369(-01) 7.24778459(-01) 6.39988075(-01) 3.93166879(-01) 2.70396296(-01) 2.09245757(-01) 1.71750051(-01) 1.45972614(-01) . . . . .

Table 6. Solutions affected with error's response.
t	y' +ty=0	y" +ty' +y=0	True	exp
0.1 0.2 0.3 4.8 5.3 5.7 5.8 9.6 13.2 13.3	9.9501247 9.8019867 9.5599747 9.9309967 7.9517440 8.8123642 4.9590409 9.8055567 1.4567406 3.8621109	9.9501247 9.8019867 9.5599756 9.9511737 8.1370781 1.05(-6) 6.64(-7) 9.98(-8) 7.22(-8) 7.16(-8)	9.95012479 9.80198673 9.55997478 9.92949522 7.94938558 8.80816483 4.95639984 9.72094942 1.45970747 0.00000000	0 0 0 -05 -06 -07 -07 -20 -37 -38

. . If the initial values are y(0)=0, y' (0)=1, the solution is obtained stably as in Table 7 because it is the impulsive response expressed in Eq.(1.33).
. . There is one more cause, which comes from the error of interval. If the interval h is a decimal of five-significant figures, for example 0.014159, the five-digit calculus obtains t₀+h=12.314 for t₀=12.300 so the valid interval h is 0.014000 and the 3rd decimal place may have a rounded error in some case of t₀. Usual methods of integral use h=0.014159 for h×f so the results lose a lot of accuracy in case of such differential equation as Eq.(1.24). Although we usually use 0.1, 0.01, etc. as the interval, these are recurring decimals in binary system and come to the results mentioned above.
. . Table 8 represents the values of the solutions of Eq.(1.24) and (1.27) without error for above t. It shows that if the 3rd decimal place of t has the least error, the results come to three accurate figures. In case of the numerical solutions, it comes to more worse results because the intervals are not equidistant, where a half of the decimal places is different.


t=12.31400…	t=12.31415926535…	t=12.31500…
4.48846403…×10⁻⁶	4.48774923…×10⁻⁶	4.48397781…×10⁻⁶
1.18294852…×10⁻³³	1.18063078…×10⁻³³	1.16847043…×10⁻³³

. . Table 8 shows also that the true solutions for comparison of accuracy must be calculated with the caution mentioned above. The five-digit calculus can't use the value t₀+h=12.314159 so it is impossible to obtain the values of the middle column. If a method obtains the values of five-significant figures of the middle column for t=12.314, the method can't obtain the values of the left column or it may be unstable and obtain the both values alternately. Therefore the best results which may be obtained by numerical solutions should be the values for t=12.31400…, that is, the values of the left column.
. . Because of these reasons, the procedure [3] in Eqs.(1.2) uses the interval h₂=x₂−x₀ instead of 2h and Program 1 uses the substitution of X#=X to calculate the true solutions for comparison of accuracy.

Return to CONTENTS